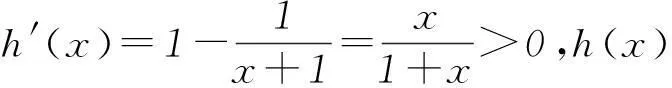精彩呈现导数命题中的分类讨论



精彩呈现导数命题中的分类讨论

◇山东卞文

导数是中学数学中的重要概念之一.分析近几年的高考题中,导数在解决函数单调性、极值、最值的应用备受命题者的关注及青睐,但导数问题也是考生的难点之一,究其原因,导数问题常伴随着参数,解题中需要对参数进行分类讨论．那么其中所涉及的讨论都有哪些呢?

引例(2015年山东卷) 设f(x)=ln (x+1)+a(x2-x), 其中a∈R

(1) 讨论函数f(x)极值点的个数,并说明理由.

(2) 若∀x>0,f(x)≥0成立,求a的取值范围.

(1) 函数f(x)=ln (x+1)+a(x2-x),其定义域为(-1,+∞),

f′(x)=1/(x+1)+a(2x-1)=

设g(x)=2ax2+ax+1-a.

其中涉及的分类讨论如下：

1) 对二次项系数的讨论.

本题求导后,导函数为二次函数型(局部为二次函数型),其中二次项系数含有参数,导函数零点的个数与参数范围有关,须对二次项系数取值进行讨论．

当a=0时,g(x)=1,f′(x)=1/(x+1)>0,函数f(x)在(-1,+∞)为增函数,无极值点.

当a>0时,Δ=a2-8a(1-a)=9a2-8a.

2) 对判别式的讨论.

当二次项系数不为0时,若导函数可因式分解,则直接求出导函数零点．否则需要讨论判别式的正负．

当Δ≤0时,得0

当Δ>0时,得a>8/9.

3) 对2根是否在定义域范围内的讨论.

设g(x)=0的2个不相等的实数根为x1、x2,且x10,则

-1

当x∈(-1,x1),g(x)>0,f′(x)>0,f(x)单调递增;

当x∈(x1,x2),g(x)<0,f′(x)<0,f(x)单调递减;

当x∈(x2,+∞),g(x)>0,f′(x)>0,f(x)单调递增.

因此，此时函数f(x)有2个极值点.

续解当a<0时,Δ>0,但g(-1)=1>0,x1<-10,f′(x)>0,f(x)单调递増;

当x∈(x2,+∞),g(x)<0,f′(x)<0,f(x)单调递减.所以函数只有一个极值点．

4) 对最值存在条件进行讨论.

(2) 由(1)可知当0≤a≤8/9时f(x)在(0,+∞)单调递增,而f(0)=0,则当x∈(0,+∞)时,f(x)>0,符合题意;

当8/90,符合题意;

当a>1时,g(0)<0,x2>0,所以函数f(x)在(0,x2)单调递减,而f(0)=0,则当x∈(0,x2)时,f(x)<0,不符合题意.

综上所述,a的取值范围是0≤a≤1.

总之,在处理导数综合问题时,只要熟练掌握处理相关问题的理论基础,明确讨论的目的,准确确定分类的标准,即可有理有据解答问题．当然针对不同的题型,分类讨论的形式不仅局限于本文所述,但只要我们在学习中注重归纳总结,即可以不变应万变．

(作者单位：山东省青岛市崂山区第一中学 )