“精诚所至，真理为开”

孔炳兴

【摘要】 小学数学教学中， 教师要重视猜想验证思想方法的渗透。猜想与验证的探究过程首先是感知阶段，通过对问题情境的全面了解为下一步探究打下基础。假设则在于对问题进行了尝试性的研究，研究的结果正确与否可以通过实例验证来判断，而归纳则使研究形成了规律性，有助于深化理解并灵活运用。学生在此过程中，不仅获得知识，更有获取知识的能力、探究知识的自信心与积极性。

【关键词】 小学数学 猜想验证 感知 归纳

【中图分类号】 G623.5 【文献标识码】 A 【文章编号】 1992-7711（2016）03-075-03

猜想验证是一种重要的数学思想方法，著名的“哥德巴赫猜想”为我们进行数学学习树立了典范。现实数学教学中，教师普遍对猜想这一环节重视不够，特别是有的老师担心学生会因些而把课堂猜乱了；对于验证，也有教师认为是多此一举的，认为这样操作太浪费时间，倒不如多解题、会解题来得实惠，这是一种短期教育的目光。科学家牛顿说过，“没有大胆的猜测就做不出伟大的发现”。小学数学教学中， 教师要重视猜想验证思想方法的渗透， 以增强学生主动探索和获取数学知识的能力， 促进学生创新能力的发展。另一方面，就思维发展特征而言，小学生处于形象思维占主导的阶段，很多数学概念、性质在小学阶段认识的，往往要到初中才去证明它，在这种情况下，小学阶段的猜想与验证起着实验教学的作用，对逐步培养学生的抽象思维作用巨大，也有助于学生创新能力的培养。

一、感知——为思维建个素材的仓库

人类认识事物是从感知事物开始的， 而后才可能认识事物的本质。学生在数学相关内容的学习中感知越丰富， 建立的表象会更清晰， 就越能发现事物的规律。

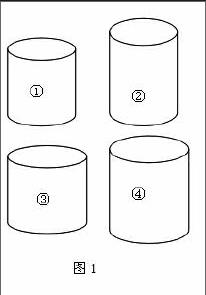
感知需要建立可行的情境条件，如用多媒体演示： 圆柱体由图①逐渐变成图②（底面不变，高扩大），再由图②变成图④（底面扩大，高不变），然后再由图①逐渐变成③ （底面扩大，高不变），再变成④，通过将图片作透明化处理后拖动鼠标比较体积的大小，学生感知到圆柱体体积与底面大小与高密切相关，这就为下一步的探究打下了思维的基础。（图1）

感知需要充分调动多种人体感官的参与，陶行知对此有“六大解放”的论述：“解放儿童的头脑，使之能思”——思维的参与感知才能加工而深化；“解放儿童的双手，使之能干”——动手摸一摸，量一量，做一做，感知才真切；“解放儿童的眼睛，使之能看”——眼观六路，感知才鲜活有效，便于形成表象；“解放儿童的嘴，使之能讲”——说一说有助于知识的反馈与消化。“解放儿童的空间，使之能接触大自然和社会”——感知的世界全面，获得的信息既真实又鲜活。“解放儿童的时间，不逼迫他们赶考，使之能学习自己渴望的东西”——时间充足才能让信息流入大脑。上述圆柱体体积的感知过程给了学生充足的时间，引导学生动眼看一看、动手做一做、动脑想一想、动笔算一算、动口说一说，从而获得丰富的素材，建立较清晰的表象，搭建起知识内化的桥梁，这样就便于形成较合理的猜想，避免不切实际的幻想与瞎想。

二、假设——为思维插上想象的翅膀

假设是对知识做出未经证实的初步判断， 它是学生获取数学知识的重要环节。在学生大量感知相关知识内容并建立了表象后，教师要给学生充足的时间与空间，让他们根据自己的思考自由地观察、分析与推理，必要时再提供一定的思维支撑，使感性知识进一步理性化，然后再通过相互交流形成合理的假设。

如教学 “分数化有限小数”时， 先提供两组最简分数，第一组比较简单：“，，，，，，，”，而第二组相对复杂：“，，，，，，，”对于第一组，让学生算一算、想一想，并猜测的分母与这个分数能化为有限小数之间有何关系？ 而对于第二组，则让算后进一步猜测： 一个最简分数如果能化成有限小数， 与这个分数分母之间可能存在什么样的关系？经过探究，学生就会形成一个结论：最简分数如果能化成有限小数，与分母的特点有关系， 如果一个最简分数的分母只含有2与5的质因数，那么这个分数就可以化成有限小数。这里教师如果只是出现第二组题，学生的猜想可能无从下手，而第一题正起到了铺垫的作用，学生在得出2与5这两个分母在化为最简分数中的特征后，就可以为第二组的猜想打下基础，他们会顺水推舟地去往2与5的方向思考，从而去分析这些表示分母的数的质因数情况。无疑，假设的作出也不是凭空而生，需要建立在科学研究的基础上，教师的引领不可忽视。

假设的作出需要一定的勇气，“两个铜球同时落地”的故事家喻户晓，故事的主人公伽利略从多次观察不同质量的冰雹落地的过程中，顶住被世人饥笑、甚至性命安全的巨大风险，大胆地提出自己的设想，最终却获得世人的认可，在科学史上留下了灿烂的一笔。作为教师，需要对不同的观点抱以倾听的态度，在学生提出错误的设想时，不妨让他说说是怎么想到的，当学生说出自己的思考过程时，大家也许把他的想法稍做调整，真理就在眼前了。“失败乃成功之母。”很多时候，大胆的设想在探究中起着举足轻重的作用。“勇气比正确性更为重要。”抱着这样的态度，学生才会敢想而会想。

假设的作出还需要借助大胆的想象，甚至需要跳出框框、打破传统来研究问题。在学生学会了长方形面积的计算、但还没有学过三角形、梯形面积计算时，有一次笔者出示了图2实线所示的梯形，要求学生通过丈量计算它的面积，学生会感到无从下手。这题如果还是从切割入手，学生的基础是不能达到结果的。事实上，学生只要设想这个图形是长方形的一部分，通过用纸片盖住并描出这个梯形，把纸片旋转后如图放置，很快就可以发现两个相同的梯形正好拼出一个长方形，这样先计算长方形面积，再除以2，就可以得到答案了。“异想天开而得求得真理”，假设的过程，需要教师给学生更多的鼓励与宽容，给学生更大的视野，而讽刺与否定只会浇灭学生探究的愿望。

三、验证——为思维把握合理的航向

猜想的结论是否正确，有待进行检验。由于小学阶段一般不要求进行规范而严格的数理论证，学生的假设是否具有普遍性，学生可以从已有的经验入手，进行独立究与小组合作探究，经历尝试、探究、验证的过程，获得验证一个命题的能力。

以“三角形的内角和”的教学为例，在学生提出猜想后，我们可以从多个角度引导学生进行验证：1.拼一拼：把三角形的几个角剪下来再拼到一起，用直尺验证拼成的新角是否两边在同一直线上。2.折一折：根据教材的提示把三个角折叠到一块儿，看内角和是否是180°.3.算一算：把手头的三角板的每一个角都量出来，并相加。4. 把正方形的纸片沿对角线分成两个完全相同的三角形， 由正方形4个角是90°，得出正方形的内角和是360°，把正方形纸片两对角顶点叠加到一起，发现刚好折出两个完全相同的三角形，展开后可以推算出每个三角形的内角和是180°。

验证是演绎思维进行的过程，验证时需要找到符合所提出观点的众多对象，观察、测量其是否具有观点所指的属性，最终把他归入同类事物中去，但是验证不可能穷尽命题涵盖的所有的对象，所以验证只能取有一些有代表性的对象来进行。但为了教学的方便，有时需要适当统一研究对象。如上述验证中的第3项教师提供的是两块三角板，如果有老师把它设计成让学生自己画一个三角形，通过量出每一个内角的度数再相加，由于误差的不可避免性，这段教学往往会陷入僵局，比如有学生说他两个三角形的内角和都是179°，教师再强行地规定是180°，就会显得强硬而没有说服力。

随着计算机技术的普及，必要时教师也可以借助软件来引导学生进行验证，以三角形内角和的验证，教师只要运用几何画板画出一个任意三角形，然后把三个角的度数通过度量选项表示出来，然后用公式选项把三个角相加就可以了。软件的一大优点是可以拖动改变图形，这时无论你怎么拉动三角形的边使之不断调整内角的大小，其三内角和始终是180°。（图3）

四、归纳———收获思想方法的果实

知识爆炸时代，每个人面对着纷繁的信息，如果不加以整理，那就会杂乱无章而难以在头脑中存储。归纳是把新验证的知识用完整、简单的语言概括出来的过程，是从特殊到一般、从具体到抽象的过程。

人教版六年级下册“数学思考”中有这样一题： “6个点可以连成多少条线段？8个点呢？”学生一动手就觉得很乱，无法数出结果。通过教师引导，学生从最简单的情况开始研究，即2个点能连成几条线段？再多些，3个点能连成几条线段？教师根据学生画图、计算列出下表（图4）：3个点连成线段的条数：1+2=3（条）；4个点连成线段的条数：1+2+3=6（条）；5点连成线段的条数：1+2+3+4=10（条）……这样学生就能很快得到答案，如果这道题只是这样解完了之，那是十分可惜的，如果有100个点呢？又怎么表示与计算呢？显然需要让学生归纳出一种方法来实现“解一题，会一片”的结果，这里关键在于搞清算理：每增加1个点，这个点可以和前面已有的每个点都连一条线段，所以前面有几个点，就会增加几条线段。教师还可以让学生把本题的规律用字母表示，并归纳结论：如果平面上有n个点，可连线段的总条数就等于从1开始至前（n-1）个连续自然数的和，也就是连续自然数的个数比题目提供的点数少1。这一思考题的归纳让学生不但知其然，更能知其所以然，提升了思维品质，教学起到了举一反三的作用，而且通过画图渗透了数形结合的数学思想，这就把知识学习提高到了能力培养的高度。

归纳时，教师要引导学生进一步分析结论存在的普遍性与适用性。比如在归纳“比的基本性质“时，要让学生想一想：性质中的“相同的数”是不是什么数都可以呢？这又是为什么？这样学生就明白了，相同的数的要求一是需要相同，二是不能为零。此外，教师要让学生理解结论中的每一层含义，避免词不达意，对于难以全部文字表述的可以用字母与式子来替代。

布鲁纳认为：“学习者在一定的问题情境中， 对学习材料的亲身体验和发现的过程， 才是学习者最有价值的东西。”如果说，感知阶段重在问题情境的全面了解，假设则在于对问题进行了尝试性的研究，研究的结果正确与否可以通过实例验证来判断，而归纳则使研究形成了规律性，有助于深化理解并灵活运用，学生在此过程中，获得的不仅是知识，更是获取知识的能力、探究知识的自信心与积极性，从而实现新课程倡导的三维目标。让学生在数学学习中的过程中享受探究的乐趣，真理会一步步向我们走来，数学课堂也能因此而美丽！

[参考文献]

[1] 严丽荣.学生数学猜想意识的培养[J]. 湖南教育. 2000（03）

[2] 张婷.实验：引领学生步入数学秘径——数学实验的教学价值例谈[J]. 新课程导学，2016（02）.

[3] 李娜.信息技术在小学数学教学中的应用[J]. 中小学电教（下半月），2016（01）.