数学教学不妨“将错就错”

曹武胜



数学教学不妨“将错就错”

曹武胜

学生在学习过程中出现了错误，很多教师总希望能狠狠地堵上这些错误，并将错误扼杀在摇篮之中。英国哲学家、数学家怀特黑德有句名言：“畏惧错误就是在毁灭进步。”教师不能把所有的路都给学生设好了，不断地堵住错误，准确无误地把所有的知识告诉学生。这样做只会让学生越来越感到学习没有挑战性，没有刺激，平淡无味，结局只会是“错误堵不住，春风吹又生”，教学效果也会越来越差。笔者认为数学教学中应该“将错就错”，在教学中留一些“岔路口”，让学生自己去选择，或故意让他们走上“歧途”，“摔摔跟头”。俗话说“吃一堑，长一智”。学生只有吃“堑”吃多了，才会长出更多的“智”。

一、制造错误，妙引新知

总是正面地传授新知，永远一本正经地按流程授课，会让学生感到乏味无比。如果平静的湖面上能激起一些浪花，对教学将有锦上添花的作用。

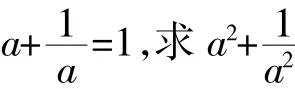
制造错误，让学生内心的不平衡在疑惑与争议中找到了平衡，能够激发学生的求知欲望。

二、设置陷阱,期待出错

没有错，学习就不会进步。学生出错，教师才好引导和点拨，学生的疑惑才能解决，教学才会有效果。对学生常出错误的地方，我们期待学生早一点出现。当学生出现错误时，教师不必急于指正，可以让学生自己去探讨，自己悟出错误原因，从分析错误中学会反思。这样学生才能深化对知识的理解。只有教师对学生可能出错的地方做到心中有数，才能更好地应付学生的错误，防患于未然。

这是一道有陷阱的题，学生往往不考虑函数的定义域而直接用奇偶函数的定义解答：由题意得f（-x）=f（x），从而得出f（x）是偶函数。此时，教师可浇他们一盆冷水——答案错了。一开始学生还不服气，坚持认为自己的解法没错。学生的质疑、反对，能够使思维总是处于活跃状态。这正是教学所需要的。接下来，教师让学生自己找错误的原因，认真地思考、讨论。学生发现，原来是忽略了一个重要条件——定义域。函数的定义域不关于原点对称，所以它是一个非奇非偶函数。

设置陷阱让学生出错，是为了学生能早一点改正错误。学生出错后，让他们自己找出错误的原因，更能发现自己的不严谨和不细心，就更能警示自己：“不要定式思维，要缜密思考，注意隐含条件，不要再犯类似错误！”这比教师苦口婆心地反复提示效果要好得多。

三、教师“出错”，学生找错

一些学生常出的错误，如果直接提醒，往往不能引起他们的重视。教师不妨在板演的过程中故意给出一个错误的演算，通过貌似正确的推理得出似乎合理的结论。这时，一些细心的学生会发现老师的错误，当然会非常有成就感，上课也会更专注。如此故意展示错误，让学生意外发现错误，引起讨论与探究，学生会为自己这种意外的发现感到惊喜，从而主动寻找正确的解法，教学效果也会更好。

教师故意板演错误的求解过程：

解：由基本不等式得：原式≥22+22=8，所以原式的最小值为8。

一开始学生觉得没错，但慢慢地出现了异议，指出老师的解法有问题。“老师也会出错吗？”平静的课堂一下子热闹了。学生在相互交流中终于发现了错误，指出“=”取不到。学生经过努力，终于得到了正解。原式的最小值为（a=b=时取得）。

教师故意出错，相当于给学生打了一次“预防针”。学生找到错误，无形中提高了自己的“免疫力”，大大减少了以后犯错误的几率。

四、反例纠错，错出智慧

教师在教学中，要说明一个命题正确，必须在给定的条件下，严格地用逻辑推理的方法推出，但要说明一个命题错误，只要举一个反例即可。由于定式思维的影响，学生经常会遇到一些难以判断的错误命题，此时一个反例常常会让学生茅塞顿开，反例能够起到点石成金的作用。

五、作业找错，改变批改方法

作业能及时反馈教学的效果，有效地解决作业中的错误，有利于及时调节教学方式。传统的教师“全批全改”作业的方式，形式单一，且效率低，教师可改变一下作业的批改方式。

随堂改：对于“概念型”或“答案型”的简单题目，可以在课堂上让学生自己改，自己分析出错误原因。

变形改：师生互换，教师做作业，学生改作业。教师精选一些易错题组成一份“变形作业”，“有心机”地去做这份作业，将学生常见的错误在作业中展示出来。做完后，将“变形作业”印发给学生，由学生评改。学生们长期被老师评价，终于有机会评价老师了，会非常认真和积极地批改老师的作业，努力地寻找老师的错误，也仿照老师修改这些错误。这样的过程更有利于学生形成严谨的思维，大大提高辨错能力和解题能力。

评语改：传统的“√”或“×”会让学生乏味，在学生出错的关键地方提示一下，指出错因，会有事半功倍的效果。如：“公式用错”“解法不全”“没考虑定义域”等。

六、建立《错题反思录》，杜绝一错再错

事实上，很多学生都制作过错题本，但却没有用好它，只是机械地抄写错题与答案，缺少对错题的反思与总结，日后也不会翻阅做过的错题，导致错误一犯再犯。因此，教师要求学生建立的不只是错题本，而应该是《错题反思录》。

《错题反思录》主要记三类题。一是不会做的题。这些题说明自己存在学习漏洞，需要补全。二是会做但做错了的题。这些题反映了自己的不细心之处，必须要找出问题所在，不能一错再错。三是模棱两可的题。这说明自己对题目的理解还不够透彻，需要进行强化。记录好这些错题后，最重要的是，要在每个错题后面做好四个反思：1.属于哪个知识点？2.我为什么会出错？3.应该如何做？4.有没有更简单的方法？

除此之外，教师还要定期给学生上“错题反思课”，让学生专门整理错题，将已经会了的题从中删去，并要学生将经典错题反复温习。《错题反思录》能让学生从被动地“要我学”变成“我要学”，很好地避免一错再错。

七、以错结尾，耐人寻味

有时课的结尾不妨以错误而终，借错给学生制造悬念，留下思考的问题，为下一次课埋下伏笔。

例如，已知（x+2）2+=1，求x2+y2的取值范围。学生错解为

教师可告诉学生答案错了，学生很想知道错在哪。这时，教师可说：“欲知后事如何，且听下回分解。”学生意犹未尽，回味无穷，激发了课后的思考及对下次课的期待。

英国心理学家贝恩布里奇说：“差错人皆有之，作为教师不利用是不能原谅的。”只有让学生在错处“摔跤”“碰钉子”，充分暴露自己的不足，才能在以后的学习中反败为胜。错误是数学教学中的有效资源，如果教师能结合自己的教学机智好好利用，数学教学就会更有效。

（作者单位：郴州市湘南中学）