在知识更深处让学生明理

罗鸣亮

英国学者P.Ernest说过：“数学教学的问题并不在于寻找最好的教学方式，而在于明白数学是什么……如果不正视数学知识的本质问题，便解决不了教学上的争议。”数学知识的本质，既表现为隐藏在客观事物背后的数学知识、数学规律，又表现为隐藏在数学知识背后的本质属性。因此，作为一名小学数学教师，理应对数学知识的产生、性质以及结构有所了解，理应理解数学知识内涵、掌握数学知识本质的呈现方式，并通过数学课堂引领学生深入数学本质，明确知识产生之理。

一、体验知识产生之理

数学知识包括数学概念和数学规则，而数学概念是数学知识的“细胞”，是学好数学知识的关键。学好数学概念，就意味着掌握了一类对象的本质属性。在小学数学中，很多概念都有丰富的形成过程。当我们的教学只是教数学“定义”时，其教学过程必然是知识模仿、记忆与强化训练，学生根本无法理解知识本质。只有让学生经历知识产生的必要性、充分感知、体验知识的产生过程才能理解知识的本质，把握知识之间的本质联系。

例如，在教学《小数的初步认识》一课时，教师都认为这一知识学生已有生活经验，不需要怎么教学生就会了，导致学生学习后仍对小数的认识不深刻，对小数的理解也说不出个所以然来。课到最后，学生仍存在困惑：“我们都学习了整数，为什么还要学习小数”、“为什么米就是0.1米呢”。追溯小数的产生，我们知道，人们在度量物体的过程中，总是把容易感知、经常接触的量作为合适的单位，如：一尺、一斤、一元等，可是，由于日常生活需要，还需要比“1”更小的计量单位。于是根据十进制发展出尺以下的寸、分；斤以下的两、钱；元以下的角、分等。根据小数的产生过程，我们在教学中应从实际测量活动入手，让学生在自主测量物体的时候，发现量得的长度会比整数米多一些或者少一些的度量情况，产生需要用新的数来表示的需求。这一过程，让学生于活动体验中，深刻感悟小数产生的必要性。此外，小数本质是十进制分数，是对整数的延伸。这一本质教师不能简单地告知，而要在教学中联系生活中的货币、长度单位，借助米尺、人民币等实物，让学生根据已有的知识经验，借助米、分米、厘米和元、角、分的十进关系，来帮助理解小数的十进关系。商品价格和物品长度学生在生活中已经有充分的认识，认识一位小数时，教师可以由商品价格引入，引导学生联系生活经验，发现：1元=10角，所以元=0.1元=1角，通过把1元平均分成10份，表示出零点几元的活动，初步感知小数的意义；再到以“米”为单位表示几分米的数量，进一步积累对小数意义的感知。在此基础上，出示用正方形表示的“1”，并通过分一分、涂一涂等活动，引导学生学会一位小数的图形表征方法，获得对小数意义的理解。这样教学，不但能帮助学生建立“零点几就表示十分之几”的认识，还有利于学生深刻感受分数、整数和小数的内在联系，促进了学生对小数知识本质的深入理解，使得知识学习深刻而有意义。

二、追溯知识本源之理

数学知识有着脉络明晰的逻辑起点，它不是一个个单独的个体，它是由无数的知识点串成的一个知识体系。在不同的知识点中，都能找到连接新旧知识的生长点。因此，我们应该而且必须引领学生回溯知识的本源，纠其根本，洞察数学知识的萌芽点、连接点和生长点；要立足于知识的生长点，让学生在新旧知识的联系中，引发思考，联通新旧知识，从而把握知识本质。

例如，人教版四年级下册《角的度量》一课，追溯度量这一知识本源，就是所要度量的物体里含有多少个单位个体的数量。为此，度量角就是通过确立一个统一的单位作为标准对所要度量的角进行比较，从而得到的一个具体的“数”，这个“数”就是对角大小的一种描述。现实教学中，许多教师却总遇到这样的困惑：不管怎么教，依然会出现一部分学生对用量角器量角这一技能无法正确掌握。有的教师甚至总结出“中心对顶点，零线对一边，再看另一边”的口诀，学生解决问题却依然还是错误不断。深究其因，是没有把握度量的本源去引发学生深入思考而导致的错误。

回顾已有度量这一知识体系中，学生已经学会度量长度、面积、时间等相关知识，教师要唤醒学生已有的认知，促使其深入思考角的度量和已学过的度量有什么相同的联系，从而发现：要度量角，首先要有角的度量单位。再用它来看看所要度量的角含有几个这样的单位，这样才能度量角的大小。角的度量单位是1°，所要度量的角含有几个1°就是几度角，这才是度量角的本源。明确度量本源后，教师让学生用脑海里所建立的1°角及10°角去估一估，所要度量的角大约几度。“估角”其实是让学生利用度量的本源去思考如何量角，是量角方法的雏形，同时也让学生在量角之前就对这个角的度数范围有一个比较合理的估计。教师还可结合量角的具体活动，让学生进一步感知角的度量和长度、面积的度量本源是相同的，都要做到零刻度对齐，看终点指着几就是表示有多少个这样的计量单位。从知识的本源去把握度量的道理，能让学生更准确地掌握量角技能。

三、挖掘规则制定之理

在小学数学学习内容中，存在着大量的四则运算法则、定律、性质、公式等规则。数学规则是数学知识的重要组成部分，作为一名小学数学教师，对所教的最基础的数学知识，不仅必须从数学的视角切实知道它是什么，还需真正明白其为什么，以明确其规定的合理性和必要性。

例如，教学《笔算除法》一课，计算法则提到“从高位除起，除到哪一位，商就写在哪一位”。对于这个“从高位除起”的法则，大家已经是形成共识的，认为依法则来教学即可，并无对这一法则产生质疑或者追问。可是，回顾之前的笔算学习，笔算加法、减法、乘法都从低位算起，而除法却要从高位算起呢？这样的规定是缘何道理？笔算除法是否可以从低位算起呢？这些问题的背后就是除法法则制定的本质。其实笔算除法不管从高位或者从低位算起都是可以的，可是从低位算起，如果碰到十位、百位等数位上的数不能一次性整除，需要两次或者多次计算，使得计算过程较为繁琐（如图1）。从高位算起，其不能被整除的数，也就是余下来的数可以和下一数位上的数合起来一起计算，其计算过程较为简单明了（如图2）。这就是为什么笔算除法规定“从高位算起”背后的道理。这一教学过程，不仅让学生明理，也让其感受到数学知识的简洁美，提升学生数学学习的兴趣。

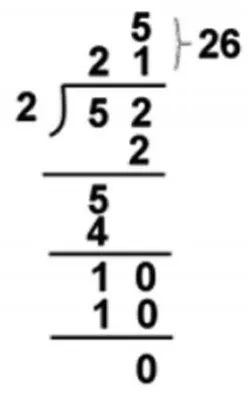
图1

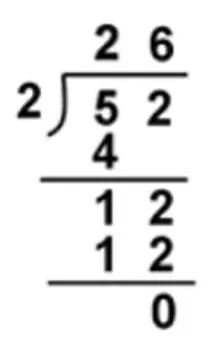
图2

数学知识都是前人的创造，每个知识的背后都有着科学的、严谨的道理，这就是知识的本质。教师自己要掌握知识本质，课堂要留给学生充足的时间，让学生去深入体会数学知识的本质，感受知识背后的道理，促进学生真正地把握知识、驾驭知识，进而推动数学课堂教学向纵深发展。