形状记忆合金悬臂梁振动固有特性试验

段　楠,滕英元,张业伟,方　勃,张　振

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)



形状记忆合金悬臂梁振动固有特性试验

段楠,滕英元,张业伟,方勃,张振

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

摘要：形状记忆合金作为一种新型的功能性材料，以其高阻尼特性被广泛的研究，并在结构振动控制方面取得了一定的应用。本文以形状记忆合金悬臂梁作为研究对象，以试验的方式测得形状记忆合金悬臂梁固定端和自由端的响应信号，从而得到其频率响应函数。然后，通过LMS Test Lab模态分析模块的PolyMAX法进行模态识别，得到形状记忆合金悬臂梁的固有频率和模态阻尼比。实验结果表明，在试验模拟工况下，形状记忆合金悬臂梁在10—65Hz的频率范围内能够很好的减弱振动源对该悬臂梁自由端的影响。

关键词：形状记忆合金悬臂梁；频率响应函数；PolyMAX；固有频率；模态阻尼比

形状记忆合金是(Shape Memory Alloys，即SMA)，是一种能够在温度或应力诱导下产生明显相变的功能性合金材料；并且，通过改变相应的温度或应力条件，形状记忆合金能从看似永久的变形下恢复到原来的形状。NiTi，NiTiCu，CuAlNi是三种常见的形状记忆合金[1]。1963年美国海军武器实验室发现近等原子比NiTi合金的形状记忆效应，是形状记忆合金作为新型功能材料被认识和研究的开始。此后，各国学者和研究人员就没停止对形状记忆效应(SME)、超弹性(SE)及高阻尼特性等形状记忆合金性能的研究[2-7]。形状记忆合金对于温度和应力变化十分敏感，在温度恒定时，其结构刚度和材料的弹性模量会随着结构的应力改变而变化，使其能应用于结构的隔振减振[8]。

Baz等[9]从理论和试验方面验证了柔性悬臂梁的弯曲振动能用形状记忆合金进行很好地控制。Rogers等[10]提出了一种将在复合材料结构中埋入形状记忆合金丝，通过形状记忆合金的特性改善复合材料结构的力学性能以及固有振动特性的思想。王振清等[11]以SMA的细观力学本构模型、振动理论以及复合材料力学为基础，研究了含形状记忆合金的复合材料梁的振动特性，建立了复合梁的固有频率与温度的方程，并利用数值结果表明SMA对梁振动行为的主动控制的有效性。李忠献等[12]建立了以形状记忆合金丝作为驱动器，抑制钢制悬臂梁的振动的主动控制系统模型，并通过数值模拟表明，该主动振动控制系统能有效地抑制悬臂梁的振动。邹静等[13]利用有限元法分析了含有形状记忆合金纤维的层合板，证明SMA纤维能很强的调节和控制层合板的自振频率和弯曲。张清泉等[14]研究了形状记忆合金梁分别在自由振动和受迫振动下的动力稳定性。秦慧增等[15]研究了含形状记忆合金薄层的简支梁的频响特性，提出了求解含SMA简支梁横向稳态频响的数学模型。Zhou等[16]利用对SMA阻尼器下简支梁的动力学行为的研究，表明了SMA阻尼器对简支梁的振动有良好的抑制作用。目前，对于形状记忆合金的理论及试验研究，主要是以丝材和薄膜作为结构的附加物或复合材料组分为研究对象[12-15]，没有以形状记忆合金(TiNiCu)板件为试验对象的相关研究。因此，以形状记忆合金自身作为减振隔振平台的相关研究是值得进行的。

本文主要使用振动台对形状记忆合金悬臂梁进行扫频，使用LMS公司的Test Lab软件进行响应信号采集，得到形状记忆合金悬臂梁工作状态下的频率响应函数(Frequency Response Function。即FRF)，再由POLYMAX算法进行模态识别[17-21]，得出形状记忆合金悬臂梁工作模态的模态频率及模态阻尼比。

1试验原理

1.1试验方法

根据悬臂梁的尺寸及安装到振动台上的方式，确定在悬臂梁及工装上选择两个点作为测量点，振动台面上一个点作为控制点，在三个点的位置粘贴加速度传感器，如图2所示。振动台面，通过直接与振动台扩展台面连接的加速度传感器、LMS测试系统、功放以及振动台构成了闭环控制回路，用闭环控制回路控制振动台面，使振动台准确的按照LMS测试系统设定的频率—响应谱线进行扫频，如图1所示。

在试验过程中同时测量形状记忆合金悬臂梁的输入和输出信号，即工装上的响应信号和形状记忆合金悬臂梁自由端的响应信号(如图2)，这样就能得到形状记忆合金悬臂梁在工作工况下的频率响应函数(FRF)，从而确定形状记忆合金悬臂梁的工作模态参数，如固有频率及模态阻尼比。

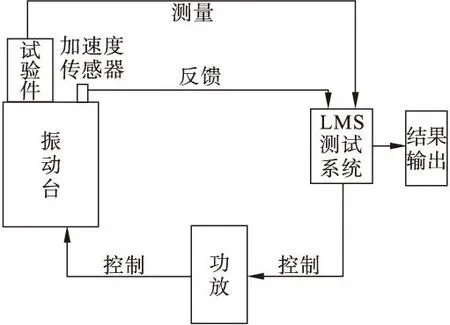
图1　试验原理框图

1.2试件材料及安装

试验中使用的形状记忆合金为TiNiCu合金，试件基本尺寸：整件长度160 mm、宽度12.5 mm、厚2 mm；安装完成后悬臂长度为120 mm。

试件通过工装安装在振动台垂向扩展台面上，工装的作用是将试件固定成悬臂梁并与振动台扩展台面连接，以达到试验要求的工况。并在悬臂梁自由端和固定端的工装上粘贴上加速度传感器，用来采集相应的数据。在扩展台面上靠近工装的位置粘贴第三个传感器，用作反馈作用，以实现多台面振动的闭环控制。试件及设备安装完成后的效果如图2所示。试验用到的设备在表1中列出。

表1　试验所用设备列表

图2　试验工况

2试验结果分析

2.1试验数据采集

试验中，设置振动台以2 g的加速度从5 Hz到200 Hz进行正弦扫频，图3中的2 g位置的平直线条即为设置的理想控制谱线；图3中的带有波动的线条为试验过程中实际测量到的振动台垂向台面的实际谱线，从图中可以看到实际的谱线和理想的控制谱线非常接近，误差非常小。

试验过程中，通过测量形状记忆合金悬臂梁自由端和固定端的响应数据，得到其频率响应函数(FRF)如图4所示。以图3所示频谱进行多次扫频试验，每次试验的FRF都与图4所示FRF曲线极度吻合，最大误差小于2%。

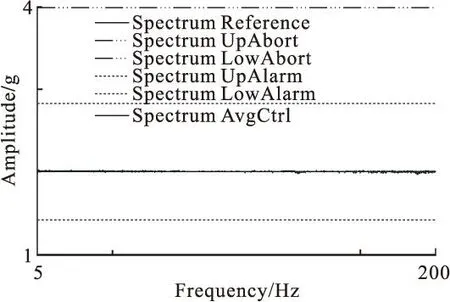
图3　扫频频谱

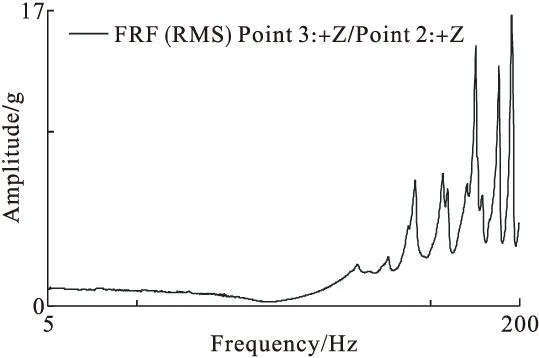
图4　形状记忆合金悬臂梁频率响应函数(FRF)

2.2数据处理

通过图4所示频率响应函数，使用LMS Test Lab 13A中Modal Analysis模块中的PolyMAX算法，识别形状记忆合金悬臂梁的模态参数，即固有频率和模态阻尼比[22]。

PolyMAX法是以频率响应函数(FRF)为基础，其数学模型为：直角矩阵分式与多项式系数矩阵：

(1)

Z=e-jωΔt

(2)

式中：[βr]是分子矩阵多项式系数；

[αr]是分母矩阵多项式系数；

Δt为采样间隔；

P是数学模型阶次；

Z是多项式基函数。

PolyMAX法设βr、αr为实值系数。

求极点和模态参与因子：在式(1)的基础上得到系统的极点和模态参与因子。

[V]=[V][Λ]

(3)

参照最小二乘法复指数(LSCF)法，在求和的频响函数图上确定稳态图，计算出响应的极点和模态参与因子，如果模态频率和模态阻尼比在规定的容差范围内不随p的不同而变化，就在求和频响函数图上标注“s”。由此得到的稳态图比最小二乘法复指数(LSCF)法得到的稳态图更清晰可靠。

识别出形状记忆合金悬臂梁200Hz以下的固有频率及模态阻尼比在表2中列出。

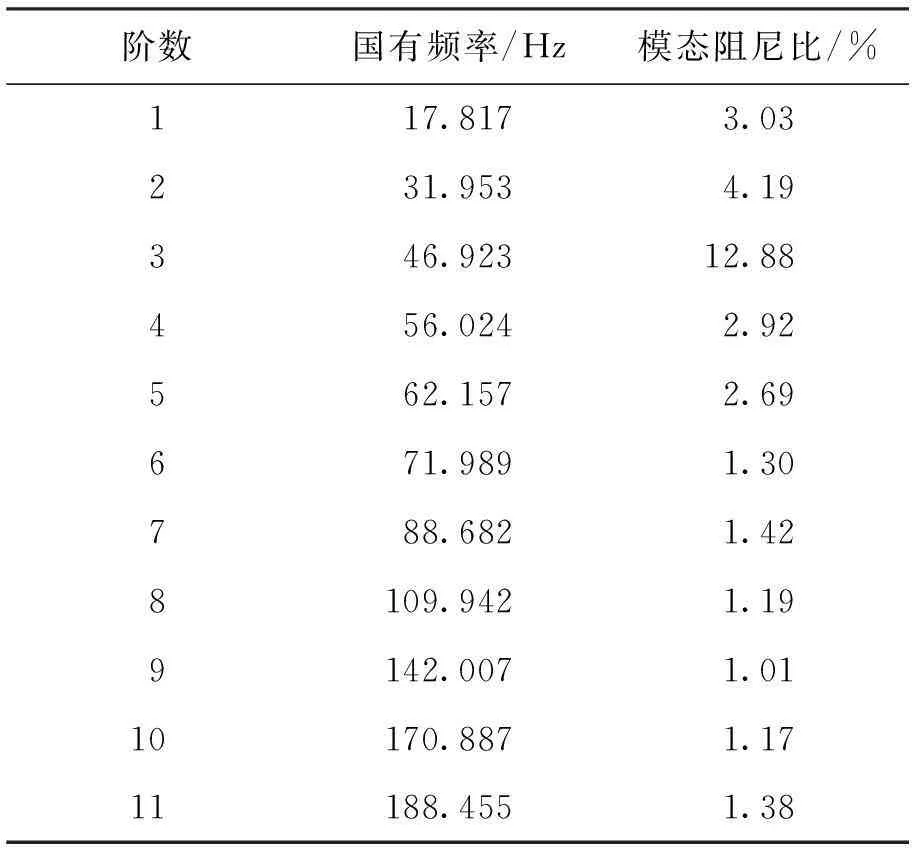
表2　SMA悬臂梁固有频率和模态阻尼比

利用PolyMAX算法的分析，识别在图3所示的扫频条件下，形状记忆合金悬臂梁具有如表2所列出的11阶模态。

(1)从表2可看出，在该试验条件下，形状记忆合金悬臂梁在各阶模态都具有较大的模态阻尼比，其模态阻尼比远高于一般的金属材料(0.01%～0.1%)；

(2)试验数据表明，形状记忆合金悬臂梁在低频段(10～65 Hz)表现出更好的阻尼性能，其模态阻尼比都在2.5%以上，尤其是在第三阶模态时，其阻尼比高达12.88%，甚至比一些阻尼橡胶的阻尼比(大于10%)更大。

3结论

本文以试验的方式研究了形状记忆合金悬臂梁在受迫振动情况下的振动固有特性。测量该类悬臂梁的响应数据，得到该类悬臂梁在频率为5～200 Hz及加速度为2 g的情况下做受迫振动的频率响应函数；并对其模态数据进行了分析。试验研究表明：

(1)在试验模拟的动力学环境下，该类形状记忆合金悬臂梁在整个工作频域内(5～200 Hz)都能够很好的抑制振动能量从振动源向工作点(梁的自由端)传递，这种抑制作用在低频段(10～65 Hz)更加显著；特别是在第三阶模态时，其阻尼能力更是超过一般的阻尼橡胶，表现出很强的吸振能量；

(2)试验结果表明，该类形状记忆合金悬臂梁在与试验条件接近的动力学环境下能很好减弱振动源对梁的自由端的影响，其能够作为一种减振平台，减弱振动源对相关设备(仪器仪表等)的损伤。并且，由于形状记忆合金不存在阻尼橡胶的耐腐蚀性差，易老化等缺点，使该类悬臂梁减振平台能够应用在很多传统阻尼橡胶不适用的环境中。

参考文献(References)：

[1]OTSUKA K,WAYMAN CM.(Eds)Shape memory materials[M].Cambridge：Cambridge University Press,1999.

[2]杨杰,吴月华.形状记忆合金及其应用[M].北京：中国科技大学出版社,1993.

[3]FENG Z C,LID Z.Dynamics of mechanical system with a shape memory alloy bar[J].Journal of Intelligent Material System and Structures,1996(7):399-410.

[4]CAO W,CUDNEY H H,WASER R.Smart Materials and Structures[J].Proceedings of the National Academy of Sciences,1999,96(15):8330-8331.

[5]超连城,蔡伟,郑玉峰.合金的形状记忆效应与超弹性[M].北京:国防工业出版社,2002:52-66.

[6]赵祥,王社良,周福霖，等.NiTi形状记忆合金材料力学性能的试验研究[J].中国科技论文,2012(2):101-106.

[7]DOLCE M,CARDONE D,Marnetto R.Implementation and testing of passive control device based on shape memory alloys[J].EeathquakeEng Struct Dyn,2000,29(7):945-968.

[8]王永军.含形状记忆合金复合结构振动特性研究[D].哈尔滨：哈尔滨工程大学,2010.

[9]BAZ A，IMAM K，MCCOY J.Active vibration control of flexible beams using shape memory actuators[J].Journal of Sound and Vibration，1990，40(3)：437-456.

[10]ROGERS C A，LIANG C，JIA J.Structural modification of simply-support laminated plates using embedded shape memory alloy fibers[J].Computer & Structures，1991(5-6)，38：569-680.

[11]王振清,王永军,周博.形状记忆合金复合梁的振动特性[J].哈尔滨工程大学学报,2011(4):434-438.

[12]李忠献,刘建涛,陈海泉.形状记忆合金复合梁的主动振动控制研究[C].南京:第六届全国地震工程学会会议,2002.

[13]邹静,钟伟芳,王兴光.含形状记忆合金纤维的复合材料层合板的弯曲及自由振动的有限元分析[J].固体力学学报,2000(1):27-32.

[14]张清泉,李映辉,姚进.形状记忆合金梁动力稳定性及混沌运动[J].四川大学学报(工程科学版),2004(5):30-34.

[15]秦惠增,任勇生.含形状记忆合金(SMA)层柔性梁的振动频响特性[J].机械强度,2002(1):45-48+115.

[16]ZHOU B，LIU Y，ZOU G，et a1.Study on structural vibration control by using shape memory alloy[J].Key Engineeging Materials，2010(417/418)：229-232.

[17]高云凯,冯海星,马芳武，等.基于PolyMAX的声固耦合模态试验研究[J].振动与冲击,2013(2):158-163.

[18]王佳,潘宏侠,杨晓波.基于PolyMAX法的齿轮箱试验模态分析[J].机械传动,2013(2):66-69+75.

[19]孙鑫晖,郝木明,王淮维.PolyMAX模态参数识别算法的快速实现[J].振动与冲击,2011(10):6-8+18.

[20]刘辉,潘宏侠.基于PolyMAX方法的齿轮箱计算模态与实验模态对比分析[J].煤矿机械,2014(1):67-70.

[21]谢小平,韩旭,吴长德，等.基于PolyMAX方法的某轿车白车身实验模态分析[J].汽车工程,2009(5):440-443+447.

[22]李青霞,任焱晞,安宏伟.PolyMax方法在桥梁工作模态分析中的应用[J].新技术新工艺,2008(7):21-23+1.

(责任编辑：刘划英文审校：隋华)

Experiment of inherent characteristics of vibration of the shape memory alloy cantilever beam

DUAN Nan，TENG Ying-yuan，ZHANG Ye-wei，FANG Bo，ZHANG Zhen

(Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China)

Abstract：The shape memory alloy,as a novel functional material,is widely studied and has been applied tothe vibration control of structure due to its high damping characteristics.In this paper,the shape memory alloy cantilever beam is used as the research subject.The response signal of the fixed end and free end of the SMA cantilever beam is measured by experiments,and the frequency response function of the SMA cantilever beam is calculated.Moreover,the modal identification is carried out using PolyMAX method of modal analysis module of the LMS Test Lab,and the natural frequency and modal damping ratio of the SMA cantilever beam are attained.As the experimental results show,under the condition of experiment simulation,the SMA cantilever beam can effectively weaken the impact of vibration source on the end of beam in the frequency range of 10 to 65 Hz.

Key words：SMA cantilever beam；frequency response function；PolyMAX；natural frequency；modal damping ratio

doi:10.3969/j.issn.2095-1248.2016.01.006

中图分类号：TG139.6

文献标志码：A

文章编号：2095-1248(2016)01-0028-04

作者简介：段楠(1990-)，男，河南镇平人，硕士研究生，主要研究方向：形状记忆合金在整星隔振系统中的应用，E-mail：tupolev160@126.com;滕英元(1963-)男，辽宁沈阳人，教授，主要研究方向：材料微观力学行为模拟及智能材料物理性质和力学行为研究，E-mail：yyteng2005@aliyun.com。

基金项目：国家自然科学基金(项目编号：11402151)；辽宁省自然科学基金(项目编号：2015020106；2013024005)

收稿日期：2015-09-24