密封动力特性影响因素CFD数值分析

孙　丹，王　双，艾延廷，王克明，胡广阳，刘宁宁

(1.沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136； 2.辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136;

3.中航工业沈阳发动机设计研究所 第5研究室，沈阳 110015)



航空宇航工程

密封动力特性影响因素CFD数值分析

孙丹1,2，王双1,2，艾延廷1,2，王克明1,2，胡广阳3，刘宁宁1,2

(1.沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136； 2.辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136;

3.中航工业沈阳发动机设计研究所 第5研究室，沈阳 110015)

摘要：研究了CFD旋转坐标系技术，应用旋转坐标系将非定常流动问题转化成定常问题，建立迷宫密封动力特性求解模型，对密封流场及密封动力特性系数进行求解研究。计算进出口压比、转速、预旋等不同条件下密封的动力特性系数及涡动系数，研究了密封动力特性的影响因素，在数值计算的基础上，进一步分析了密封气流激振力的影响因素。研究表明，随着进口压力与转速的增加，交叉刚度系数k增加，直接阻尼系数C减小，涡动系数增加，对转子稳定性不利。密封内流体的周向流动是产生密封气流激振力的重要原因。

关键词：密封；动力特性；CFD；旋转坐标系；数值分析

随着航空发动机等旋转机械向高性能、大容量、高参数方向发展，密封气流激振力对旋转机械转子系统稳定性的影响愈来愈大，密封气流激振成为引起旋转机械转子失稳的重要因素[1-4]。密封的动力特性系数是评价航空发动机等旋转机械转子稳定性的重要参数[5-8]。传统的迷宫密封动力特性计算是以整体流动理论为基础的双控体法。研究表明，双控体法模型不能准确描述密封中的回流，计算误差较大，且不适用于计算复杂密封模型[9]。近年来，随着计算机技术的发展，研究者们开始CFD数值计算的研究。国外Moore[10]利用商用软件SCISEAL成功计算了具有八个静子齿的迷宫密封动特性，Toshio[11]应用CFD软件Tascflow计算分析了锥形直通齿迷宫密封模型的动力特性系数。国内很多学者[12-14]也开始采用CFD数值模拟的方法研究密封静力与动力特性。

本文应用CFD旋转坐标系技术建立迷宫密封动力特性求解模型，对密封流场及动力特性系数进行求解研究，分析了转速、进出口压比、预旋等因素对迷宫密封动力特性系数及涡动系数的影响，在数值计算的基础上进一步分析了密封气流激振力的影响因素。

1密封动力特性模型及稳定性分析

1.1密封动力特性模型

当转子在静平衡位置受到位移或速度扰动时，密封中流体对转子的作用力可由动力特性系数与转子位移、速度线性化表示为

(1)

如图1所示，气流作用在转子上，气流力就会发生变化，当扰动量是微小量时，将气流力分解为水平、垂直两个分量Fx和Fy，并对扰动参数如位移x、y作Taylor展开，保留一阶分量，气流力可近似地作为转子微小位移和速度的线性函数。

工程计算中假设支撑各向同性，本文密封动力特性求解模型均假设转子同心涡动。在同心涡动中，密封腔中静态流动参数沿周向分布均匀，动力特性系数中直接项相等，交叉项幅值相等，符号相反，即Kxx=Kyy=K，Kxy=-Kyx=k，Cxx=Cyy=C，Cxy=-Cyx=c，代入式(1)中，则气流力可表示为

(2)

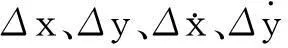
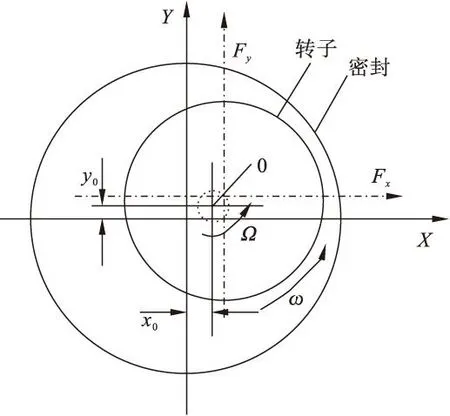
图1　密封动力特性模型

1.2密封动力特性对转子稳定性影响分析

根据文献[15]假设转子做椭圆型涡动，运动规律为

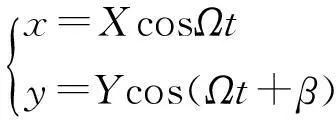
(3)

在转子一周涡动中，密封气流力对转子做功为

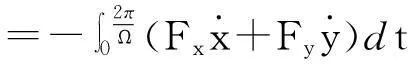
=π(Kyx-Kxy)XYsinβ-πΩ(Cxy+Cyx)XYcosβ-πΩcxxX2-πΩcyyY2

(4)

当同心涡动时，将动力特性之间关系代入式(4)，可做简化得

Wf=-2πkXYsinβ-2πΩcXYsinβ-πΩc(X2+Y2)

(5)

由式(5)可看出，主刚度系数K对应的弹性力为保守力，在轴心一周的涡动中作的总功为零，而与主阻尼系数对应的阻尼力恒作负功，消耗能量。交叉刚度系数k与交叉阻尼系数c为非保守力，在转子涡动一周中，做功可为正，也可为负，这取决于涡动轨迹形状、动力系数的大小和正负。如果在转子一周涡动中，输入系统的能量小于各种阻尼消耗的能量，那么涡动就会越来越小，转子系统趋于稳定。反之，系统就是不稳定的。

由于本文研究密封模型将转子涡动轨迹简化为圆周轨迹运动，则有X=Y=r0，β=90°，代入式(5)得

(6)

由式(6)可以看出，当k<ΩC时，W<0，流体从转子吸收能量，涡动减弱，系统趋于稳定。而当k>ΩC时，W>0 ，流体对转子做功，转子能量增加，涡动增强，系统趋于失稳。当k=ΩC时，W=0 ，转子系统处于平衡状态，涡动强度保持不变。因此为了增加转子密封系统的稳定性，避免发生自激振动，应尽量减小交叉刚度系数值，增加主阻尼系数值。

因此可用涡动系数Ωf判定转子稳定性[8]

Ωf=k/ΩC

(7)

涡动系数Ωf的值越小，转子稳定性越好。

2密封动力特性CFD求解方法

在静止坐标系中，由于转子的涡动，导致迷宫密封中的流场是非定常的，在静止坐标系下进行CFD计算就需使用动网格技术进行非稳态求解，求解比较复杂。针对该问题，本文应用CFD旋转坐标系技术，以旋转频率为Ω的旋转坐标系观察流场，则转子处于固定位置，并把这种情况作为稳态处理。图2表示旋转坐标系以及在旋转坐标系下的坐标转换，X-Y是原有的静止坐标系，τ-r是旋转坐标系，即将坐标系固连于涡动转子轴心以涡动转速旋转。在旋转坐标系下，将坐标系建立在转子轴心，这样计算区域不变，将不稳定问题转化为稳定问题，消除控制方程的时间相关项。在旋转坐标系下，静子壁面将以相反的方向旋转，转子壁面围绕轴心旋转的相对角速度为ω-Ω，密封壁面围绕原点旋转的相对角速度为-Ω。

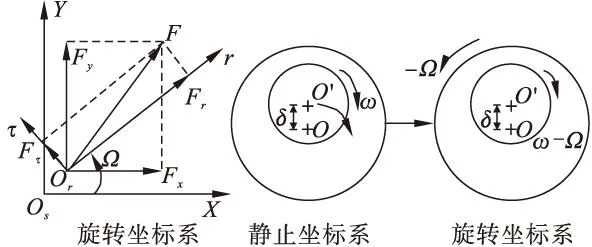
图2　旋转坐标系及坐标转换

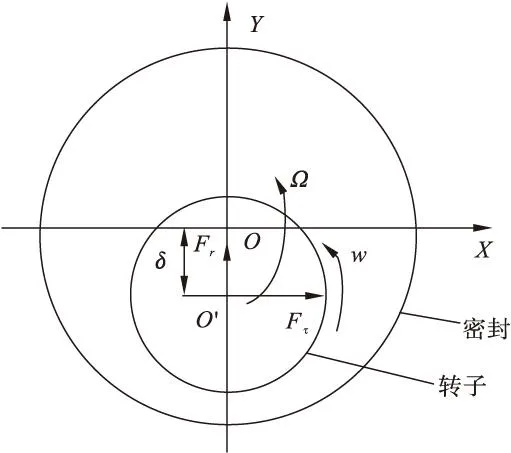
图3　密封径向力、切向力模型

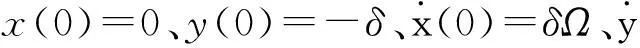
(8)

由式(8)可以看出，转子静偏心为零，当转子在偏心位置较小轨迹涡动时，密封对转子的径向力和切向力与涡动角速度Ω成线性关系。切向力Fτ是促使转子涡动的激振力来源，其由交叉刚度k和直接阻尼C决定，可以改变转子的涡动频率，促使转子失稳。交叉刚度增加，转子稳定性下降；直接阻尼增加，转子稳定性提高。

要确定迷宫密封动力特性系数，首先要计算密封中流体作用在转子上的切向力Fτ和径向力Fr。求解Fτ和Fr的关键是在一定边界条件下，计算密封中转子壁面的压力分布，通过积分转子表面压力求得切向力Fτ和径向力Fr。计算得到不同涡动角速度Ω下气流力Fτ、Fr，通过线性拟合得到气流力随涡动角速度Ω之间的线性方程，即可得出密封的动力特性系数。

3迷宫密封动力特性数值求解

3.1求解模型

为了验证本文CFD旋转坐标系动力特性求解模型的准确性，计算模型首先取自Toshio[11]的压缩机叶轮入口迷宫密封模型。Toshio应用CFD软件Tascflow对密封流场及动力特性系数进行了数值求解，并与控制体模型DYNLAB计算结果相比较，该密封模型工况参数如表1所示。

表1　外文密封模型工况参数

3.2求解模型网格划分

该文密封模型的静子带有5个锥形直齿，转子光滑，密封的几何参数与网格划分区域及最终网格模型如图4 所示。为了细化流动特性变化大的近壁面区域，相邻两节点间距比为1.1，增加在近壁面处网格密度。取密封间隙的10%作为转子涡动半径，在偏心状态下划成三维网格。将密封求解模型腔中网格划分为3个区域，为了得到合适的网格密度，研究了网格密度对计算结果的影响，计算分析并考虑计算机能力和计算时间等因素对三维模型进行网格划分，本文将网格密度n1、n2、n3、n4、n5分别确定为15、25、50、10、48，由此得到的密封模型轴向网格剖面图如图4所示。

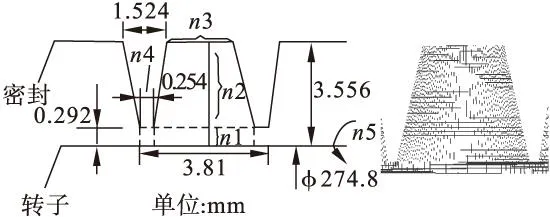
图4　模型尺寸与网格划分区域及网格模型

3.3求解结果验证

(1)速度场

图5给出根据求解模型得到的密封流场的轴向剖面速度矢量图，由图中可以明显看出迷宫密封中的流场分为两个区域，即齿顶处的射流区和密封腔中的回流区，正是齿顶的这种节流和密封腔内的动能耗散起到了密封作用。

图5　轴向剖面速度矢量图

(2)压力场

图6显示了密封内流场压力沿轴向压力呈现阶梯降低的分布规律，由图中可以看出压力降低主要发生在密封齿顶处，在密封腔内的压力值基本相等。

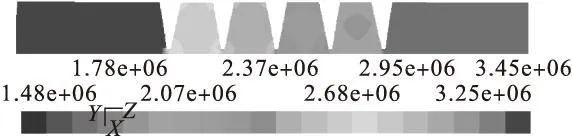
图6　轴向剖面压力分布图

表2给出了与Tascflow软件计算泄漏量结果相比较，控制体模型DYNLAB与本文Fluent软件计算结果的相对误差。由表中数据可以看出，Fluent软件求解模型与Tascflow软件求解模型计算结果相吻合。与CFD软件计算结果相比，控制体模型DYNLAB计算偏差较大。这是由于控制体模型采用的是半经验公式，其中的动能系数和流动系数的取值对计算结果影响较大。

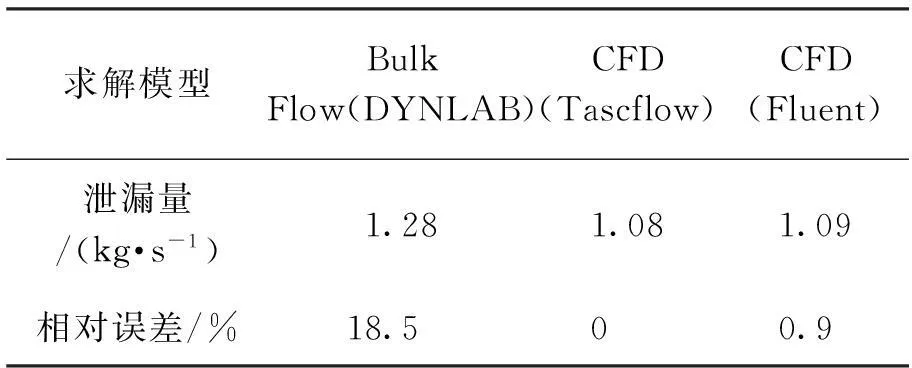
表2　泄漏量比较

(3)动力特性系数

本文分别计算转子涡动角速度为0 rad/s、290.5 rad/s、581 rad/s、871.4 rad/s、1 162 rad/s下密封内气流的切向力及径向力，得到其与涡动角速度的关系如图7所示。由该图可以看出，在静偏心为零，转子在静偏心位置较小轨迹涡动时，密封内气流对转子的气流力与涡动半径的比值与涡动角速度成线性关系。CFD求解模型计算结果与整体流DYNLAB求解模型结果具有相同的变化趋势，但CFD求解模型的气流力计算值要大于整体流模型。

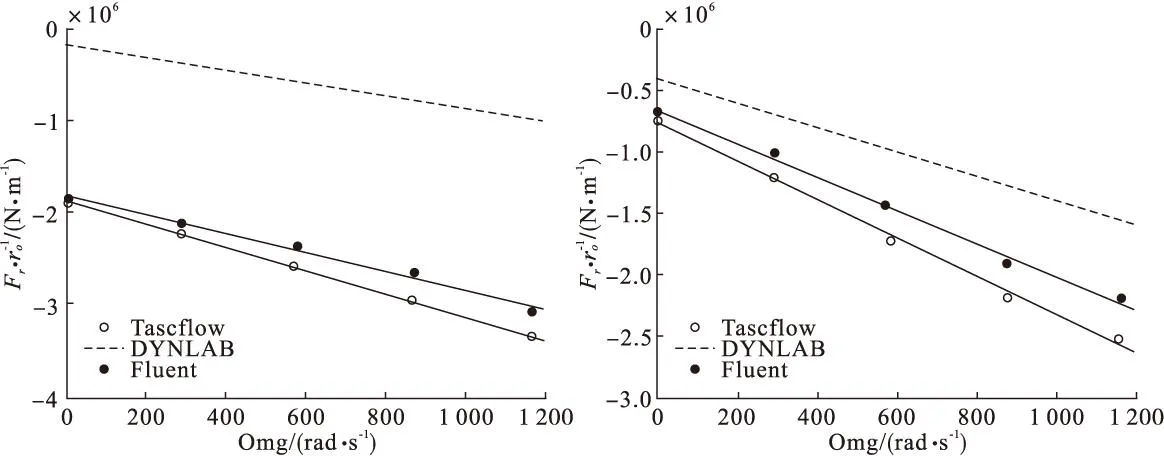
图7　径向力、切向力与涡动半径之比随涡动角速度之间关系

根据式(8)，通过CFD求解方法计算得到不同涡动角速度条件下的密封气流力，通过线性拟合得到密封气流力与涡动角速度之间的线性方程，即可求出密封的刚度系数及阻尼系数。表3给出了由径向力、切向力与涡动半径之比随涡动角速度之间关系计算得出的动力特性系数，由表中数据可以看出，本文建立的Fluent软件求解模型与Tascflow求解模型计算结果比较接近，但两者与整体流DYNLAB求解模型的结果相差较大。这是由于整体流DYNLAB求解模型是建立在一系列简化基础上，没有考虑密封流场的回流，该模型求解误差较大。

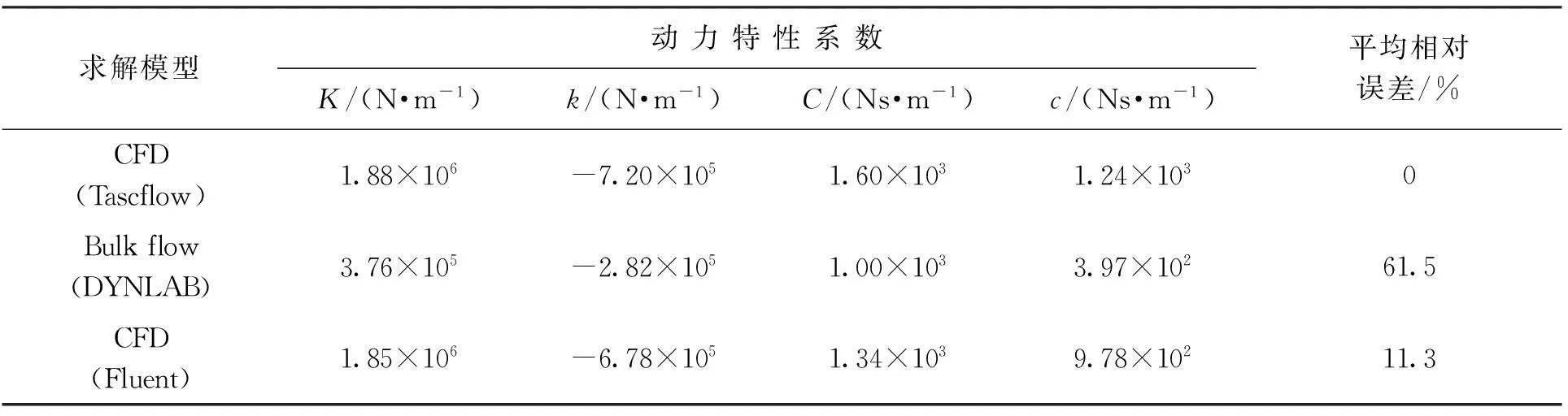
表3　动力特性系数计算结果比较

4迷宫密封动力特性影响因素分析

4.1进气压力对密封动力特性的影响

本文计算了无进口预旋速度、转速为3 000 r/min，出口压力为1.724 MPa，不同进口压力下密封的动力特性系数。图8给出了交叉刚度、直接阻尼及由此得出的涡动系数与进口压力之间关系。由图中可以看出，当出口压力一定时，随着进口压力的增加，交叉刚度系数k增加，直接阻尼系数C减小。由此求出的涡动系数增加，对转子稳定性不利。

4.2转速对密封动力特性的影响

图9给出了无进口预旋速度、进口压力为3.447 MPa、出口压力为1.724 MPa下交叉刚度、直接阻尼及由此得出的涡动系数与转速之间关系。由图中可以看出，随着转速增加，交叉刚度k增加、直接阻尼C减小，由此得出的涡动系数增加，转速升高对转子稳定性不利

4.3预旋对密封动力特性的影响

在旋转机械中，当气体进入密封之前往往有一定的预旋速度，进入密封腔室后由于动能并不能完全损失，因此气体在密封腔中不仅有沿轴向的流动，还以较大的周向速度围绕转子流动，对密封的稳定性产生一定影响。本文计算了转速在3 000 r/min下，进口压力为3.447 MPa，出口压力为1.724 MPa，预旋速度分别为-5 m/s、0 m/s、5 m/s、8 m/s下密封压力分布及径向、切向气流力，预旋速度为负代表与转子旋转方向相反，正值代表与转子旋转方向相同。为了分析预旋速度对密封周向压力高点在轴向方向上的影响，将密封模型沿轴向截取5个截面，如图10所示。

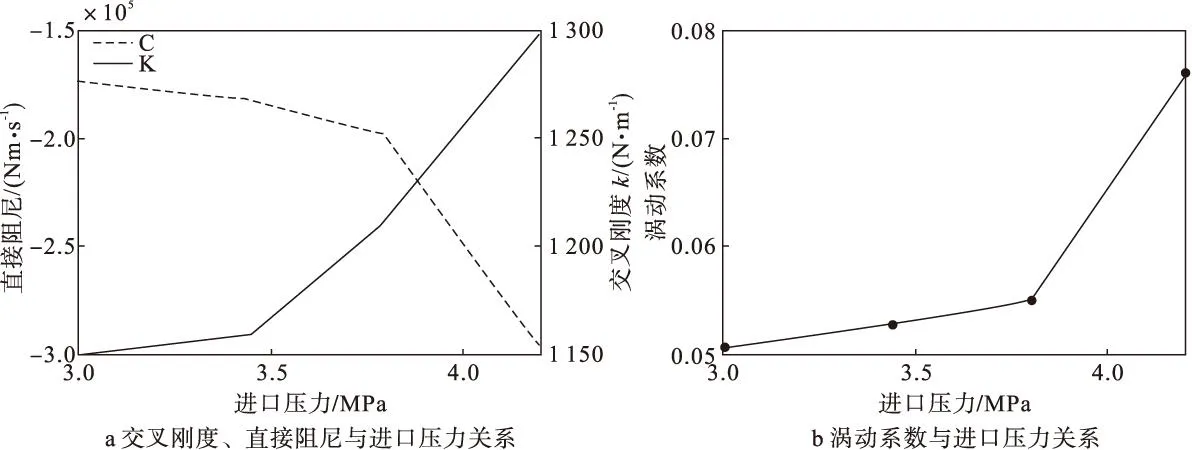
图8　进口压力对密封稳定性影响

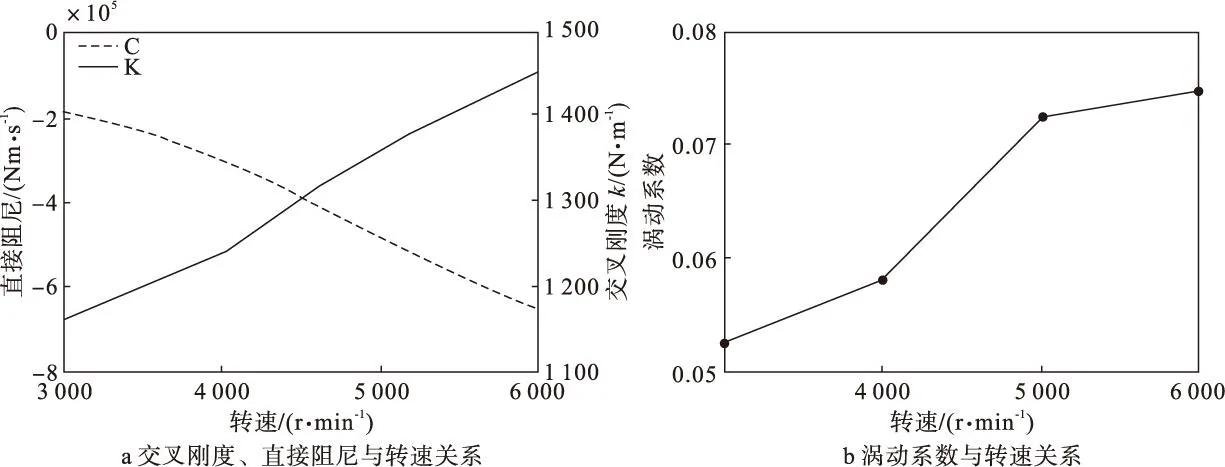
图9　转速对密封稳定性影响

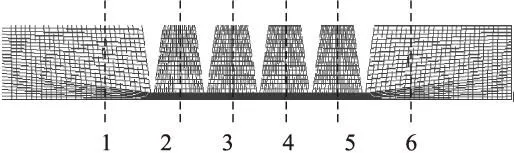
图10　轴向截面

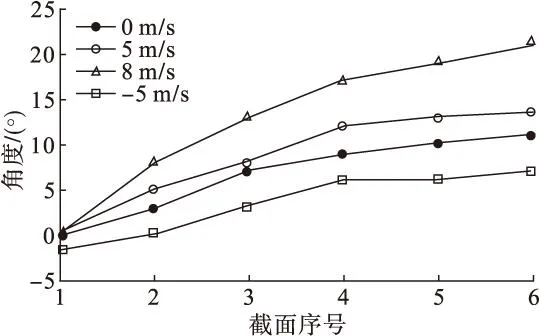
图11　轴向截面压力高点变化

图11给出了在不同进口预旋速度下的各个截面周向压力高点的变化，定义0°为密封最小间隙处，由图中可以看出，密封内流场的周向压力高点沿轴向方向上发生偏移，这是由于密封内气体产生周向流动以及由此而产生的螺旋形效应造成的。随着预旋速度的增加，沿轴向密封周向压力高点偏移的角度差在逐渐增大，负的预旋速度得到的轴向压力高点偏移量最小。

图12给出了预旋速度对密封稳定性影响。由图中数据可以看出，随着预旋速度的增加，交叉刚度显着增加。涡动系数随入口预旋速度的增加而逐渐增大，可见在迷宫密封入口的正向预旋不利于转子的稳定，在密封入口加反预旋是改善转子稳定性的有效方法。

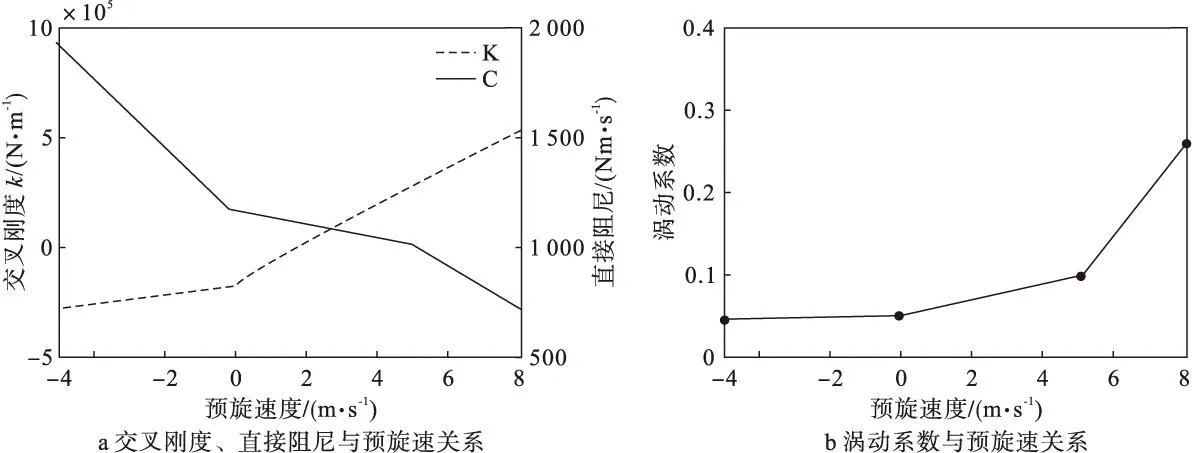
图12　预旋速度对密封稳定性影响

5结论

本文研究了CFD旋转坐标系技术，将坐标固连于涡动转子轴心的旋转坐标系，将非定常流动问题转化成定常问题，建立迷宫密封动力特性CFD求解模型，对密封流场及密封动力特性系数进行求解研究，得出以下结论：

(1)通过对密封动力特性的影响因素分析表明，随着进口压力与转速的增加，交叉刚度系数k增加，直接阻尼系数C减小，涡动系数增加，对转子稳定性不利；

(2)入口预旋交叉刚度的主要影响因素，入口预旋越大交叉刚度越大。减小周向速度可以提高转子的稳定性，密封内流体的周向流动是产生密封气流激振力的重要原因。

参考文献(References)：

[1]TIWARI R，MANIKANDAN S，DUIVEDY S K.A review of the experimental estimation of the rotor dynamics parameters of seals[J].The Shock and Vibration Digest,2005，37(4):261-284.

[2]何立东，高金吉，金琰，等.三维转子密封系统气流激振的研究[J].机械工程学报，2003，39(3)：100-104.

[3]郎骥，杨建刚，曹浩.可倾/固定密封内流体激振力计算与试验比较[J].机械工程学报，2013，49(3)：101-105.

[4]冷小磊，孟光，赵三星，等.气流激振力作用下碰磨转子的分叉现象[J].汽轮机技术，2006，48(1)：1-6.

[5]SUN D，YANG J G，GUO R,et al.A trigonometric series expansion based method for the research of static and dynamic characteristics of eccentric seals[J].Journal of Mechanical Science and Technology，2014，28(6)：2111- 2120.

[6]李志刚，李军，丰镇平.袋型阻尼密封转子动力特性的多频单向涡动预测模型[J].西安交通大学学报，2012，46(5)：13-18.

[7]晏鑫，李军，丰镇平.蜂窝密封内流动传热及转子动力特性的研究进展[J].力学进展，2011，41(2)：201-216.

[8]张晓旭，李雪松，王路遥，等.直通齿和交错齿迷宫密封流场与动特性的比较[J].工程热物理学报，2014，35(6)：1083-1086.

[9]曹树谦，陈予恕.现代密封转子动力学研究综述，工程力学[J].2009，26(SⅡ):68-79.

[10]MOORE，J.JEFFREY.Three dimensional CFD rotordynamic analysis of gas labyrinth seals[J].Journal of Vibration and Acoustics，2003，125：427-433.

[11]TOSHIO HIRANO，ZENGLIN GUO，R.Gordon Kirk.Application of computation fluid dynamics analysis for rotating machinery part II：labyrinth seal analysis[J].Journal of Engineering for Gas Turbines and Power，2005，127(4)：820-826.

[12]孙丹，肖忠会，郑铁生,等.密封切向气流力与径向气流力影响因素研究[J].润滑与密封，2013，38(9)：33-36.

[13]孙丹.旋转机械微小间隙内流体动力特性分析与试验研究[D].南京：东南大学，2011.

[14]韩强，李忠刚.汽轮机组迷宫密封泄漏量及气动特性三维CFD数值模拟研究[J].电站系统工程，2013，29(5)：12-14.

[15]钟一谔，何衍宗，王正,等.转子动力学[M].北京：清华大学出版社，1987.

(责任编辑：宋丽萍英文审校：隋华)

CFD numerical analysis of influence factors of seal rotordynamic characteristics

SUN Dan1,2，WANG Shuang1,2，AI Yan-ting1,2，WANG Ke-ming1,2，HU Guang-yang3，LIU Ning-ning1,2

(1.Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China; 2.Liaoning Key Lab of Advanced Test Technology for Aerospace Propulsion System，Shenyang 110136,China； 3.The 5thResearch Department,AVIC Shenyang Engine Design and Research Institute,Shenyang 110015,China)

Abstract：The Moving Reference Frame technology was studied in the paper by transforming unsteady flow into steady one using Moving Reference Frame method.The rotordynamic characteristics of labyrinth seal models were set up to evaluate the seal rotordynamic characteristics and flow field characteristics.The seal rotordynamic characteristics and whirl coefficients under different pressure ratios,rotational speeds,and pre-rotation conditions were evaluated to study the influence factors of seal rotordynamic characteristics,and the influence factors of exciting force produced by seal air flow were further analyzed on the basis of numerical calculations.The results,which are unfavorable for the stability of the rotor,show that with the increase of the inlet pressure and rotational speed,the cross stiffness coefficient k increases,the direct damping C decreases,and the whirl coefficient increases,and the seal fluid circumferential flow is the main cause of the seal airflow exciting force.

Key words：seal;rotordynamic characteristics;CFD;moving reference frame;numerical analysis

doi:10.3969/j.issn.2095-1248.2016.01.001

中图分类号：TK263.0242

文献标志码：A

文章编号：2095-1248(2016)01-0001-07

作者简介：孙丹(1981-)，男，辽宁丹东人，副教授，主要研究方向：旋转机械密封与滑动轴承流体激振理论与实验研究，E-mail：phd_sundan@163.com。

基金项目：国家自然科学基金(项目编号：11302133)；航空科学基金(项目编号：20140454003)；辽宁省自然科学基金(项目编号：2015020113)

收稿日期：2015-03-26