Reddy修正偶应力模型及层合板热尺度效应

吴　穹，吴　振

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，辽宁 沈阳 110136)



Reddy修正偶应力模型及层合板热尺度效应

吴穹，吴振

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，辽宁 沈阳 110136)

摘要：引入纤维和基体材料的材料尺度参数，提出了适于分析复合材料层合板热尺度效应的Reddy修正偶应力理论。此理论中将转角矢量看作独立变量，曲率张量不再对称，但可以退化为各向同性的修正偶应力。使用Reddy位移场模式，考虑温度在x轴、y轴方向引起的热应变，分析了简支板的热弯曲问题。数值结果表明，对于细观复合材料层合板热弯曲问题，材料的尺度效应不能忽略。

关键词：Reddy型修正偶应力理论；复合材料层合板；热弯曲；尺度效应

实验表明[1-2]，当金属材料尺寸进入微米量级时，材料的强度和刚度有所增强，这种现象被称为尺度效应。经典连续体力学无法解释该现象，为了分析尺度效应，各国学者相继发展了偶应力理论及应变梯度理论。上世纪60年代，Mindlin等人[3-5]提出了简化的偶应力模型。2002年，Yang等[6]重新定义曲率张量，引入偶应力力矩平衡方程，使得应变张量与应力张量对称，因而本构关系中只需引入一个材料尺度参数。2006年Park和Gao[7]研究了修正偶应力的Bernoulli-Euler梁模型。2008年Ma等[8]建立了Timoshenko梁模型。Tsiatas[9]在2009年建立了偶应力Kirchhoff板模型。2011年，Ma等[10]基于修正偶应力建立了Mindlin板模型。2012年，Alireza Nateghi等[11]研究了基于修正偶应力的功能梯度梁的热尺度效应。同年，M.Simsek等[12]对功能梯度Timoshenko梁作了静弯曲分析。2012年，Asari等[13]基于修正偶应力对功能梯度Timoshenko梁做了热后屈曲的尺度效应分析。2012年，陈万吉等[14]定义新的曲率张量并建立复合材料层合板的本构关系，认为新的曲率张量不再对称，但可以与各向同性的曲率张量等价；建立了Reddy层合梁模型[15]，根据新修正偶应力分析复合材料层合梁的自由振动问题[16]；2013年基于该理论用整体局部位移模式建立层合梁模型[17]。综上所述，各国学者基于修正偶应力分析了复合材料弯曲和自由振动问题，然而没有涉及复合材料层合板热尺度效应。基于此，本文推导了考虑热应变的修正偶应力理论，并基于修正偶应力分析复合材料层合板热尺度效应。

2理论模型

2.1位移模型

为了得到Reddy理论，首先使用如下初始位移场：

u(x,y,z)=u0(x,y)+zu1(x,y)+z2u2(x,y)+z3u3(x,y)

v(x,y,z)=v0(x,y)+zv1(x,y)+z2v2(x,y)+z3v3(x,y)

v(x,y,z)=w0(x,y)

(1)

其中，u0、v0和w0表示中面上点(x,y)的位移；u1和v1表示中面法线关于y轴和x轴的转角；u2、u3、v2和v3是沿z坐标的三次展开项。

通过使用横向剪切自由表面条件，Reddy理论最终位移场可写为

w(x,y,z)=w0(x,y)

(2)

温度场如下：

ΔT=f(z)T(x,y)

(3)

其中，f(z)为沿厚度方向分布的温度构形，T(x,y)为面内温度分布函数。

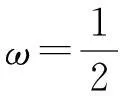
ωz=0

(4)

2.2新修正偶应力及本构关系

Yang等[6]提出的修正偶应力中，应变张量和曲率张量是对称的，定义如下：

(5)

应力张量和偶应力张量定义如下：

(6)

(7)

(8)

其中，

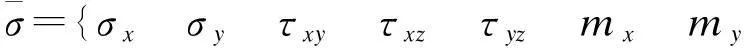
mxymyx}T

(9)

(10)

={εx-αxΔTεy-αyΔTγxyγxzγyzχx

χyxxyχyx}T

(11)

αx，αy分别表示沿x轴方向和y轴方向的热膨胀系数；

(12)

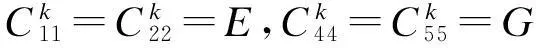
经坐标变换，第k层在整体坐标中的应力应变关系

(13)

其中，Qk=TkTCkTk,Tk为坐标转换矩阵。

(14)

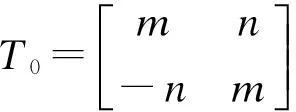
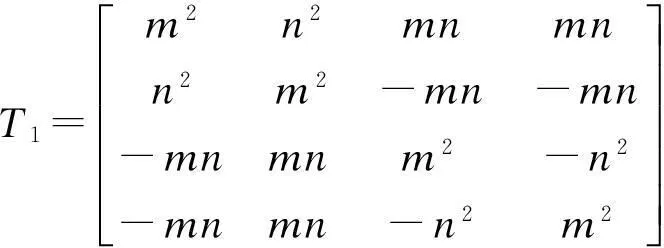
m=cosφk,n=sinφk。

2.3平衡方程

根据最小势能原理，可得到平衡方程。最小势能原理可写为，

δπp=δU-δW=0

(15)

(16)

δW=∫Ωf δudv+∫∂ΩV δuds

(17)

其中，δπp表示弹性体总的势能，δU和δW分别表示弹性体应变能和外力所做的功，f为层合板上的体力，V为在板边界处的边界力。只考虑受热载荷的影响，外载荷不再考虑，故f=V=0。

把公式(2)带入几何方程，得到宏观部分的应变，同时将公式(4)带入(5)中得到偶应力部分应变。最终都带入式子(16)中，利用变分得到平衡方程，如下：

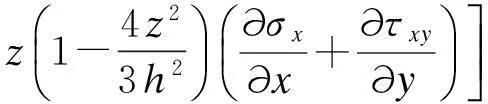
(18)

对四边简支板，位移边界条件

在x=0和x=L处，v0=0，v1=0，w0=0

在y=0和y=L处，u0=0，u1=0，w0=0

2.4解析解

在横截面(y,z)纤维断面与基体相互作用，纤维相当于是夹杂，其材料尺度参数远大于在截面(x,z)中以长纤维和基体作为夹杂的材料尺度参数[14]，即b≫m。因此对于复合材料层合板，可以假设m=0，以简化刚度矩阵。

由式子(12)和(14)，得到整体坐标中的刚度系数，如下：

(19)

为满足四边简支方板的边界条件，根据Navier方法，位移u0、u1、v0、v1和w0都以含未知系数的双傅里叶级数展开。各位移函数表示如下：

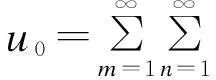
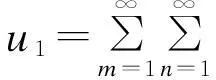
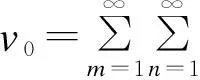
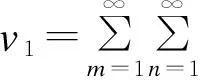
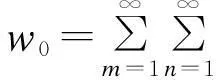
(20)

将式子(19)中的刚度系数归到式子(13)的矩阵Qk中，然后将式子(13)、(20)带入到(18)中，最终可得到式子(20)中各项系数。

3算例

为了验证微观尺度下复合材料层合板的尺度效应，采用[0°/90°/0°]正交铺设的四边简支方板。长度L=200μm,板厚h=25μm，材料的属性参数：E1/E2=15,E2=10GPa，G12/E2=0.5,G22/E2=0.335 6,υ12=0.3,υ22=0.49,αx=0.015×10-6/K,αy=1×10-6/K。

取在截面(x=L/2，y=L/2)的主应力，应力表达式如下：

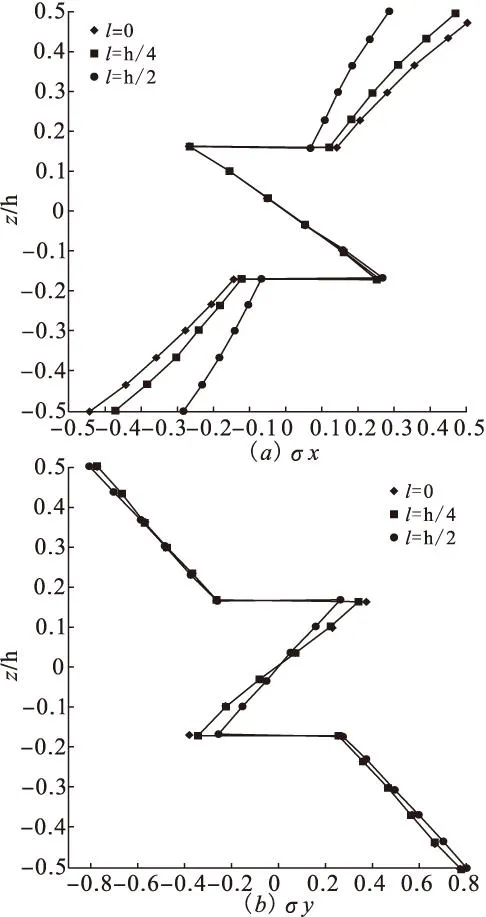
图1　在板(x=L/2,y=L/2)处的主应力δx和δy

图2给出了横向位移分布。在图中可以看到偶应力理论下板的变形要小于经典弹性力学中板的变形。

图3分别给出了层合板在x=L/2和y=L/2处板的转角。在图中可以看到随着尺度参数的增大板的转角在减小(逆时针为正)。

数值结果表明，复合材料进入细观尺度时，材料的尺度效应不能忽略。

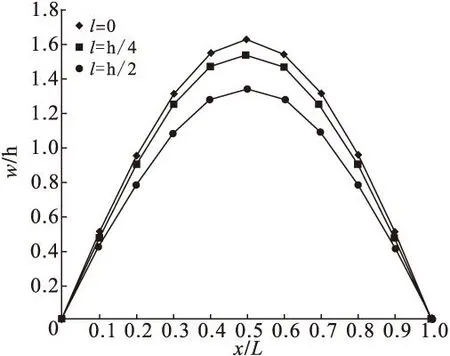
图2　横向位移(y=L/2)

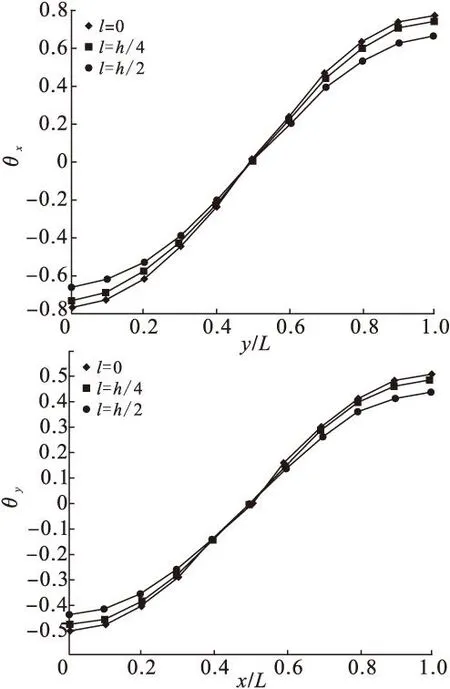
图3　转角(x=L/2、y=L/2)

4总结

参考文献(References)：

[1]FLECK N A,MULLER G M,ASHBY MF,et al.Strain gradient plasticity:theory and experiment[J].Acta Metall Mater,1994,42(2):475-487.

[2]LAM D C,YANG F,CHONG A C M,et al.Experiments and theory in strain gradient elasticity[J].Mech Phys Solids,2003,51(8):1477-508.

[3]MINDLIN R D,TIERSTEN H F.Effects of couple stresses in linear elasticity[J].Archive for Rational Mechanics and Analysis,1962,11(11):415-448.

[4]TIUPIN R A.Elastic materials with couple stresses[J].Arch Rational Mech Anal,1962,11(1):385-414.

[5]MINDLIN R D.Influence of couple-stresses on stress concentrations[J].Experimental Mechan-ics,1962,3(1):1-7.

[6]YANG F,CHONG A M,Lam D C C,et al.Couple stress based strain gradient theory for elasticity[J].International Journal of Solids and Structures,2002,39(10):2731-2743.

[7]PARK S K,GAO X L.Bernoulli-Euler beam model based on a modified couple stress theory[J].Micromech Microeng 2006;16(11):2355-2359.

[8]MA H M,GAO X L,Reddy J N.A microstructure dependent Timoshenko beam model basedon a modified couple stress theory[J].Journal of the Mechanics and Physics of Solids,2008,56(12):3379-3391.

[9]TSIATAS G C.A new Kirchhoff plate model based on a modified couple stress theory[J].International Journal of Solids and Structures,2009,46(13):2757-2764.

[10]MA HM,GAO X L,REDDY J N.A non-classical Mindlin plate model based on a modified coup-le stress theory[J],2011(220):217-235.

[11]ALIREZA N,MAZAHER S.Thermal effect on size dependent behavior of functionally graded microbeams based on modified couple stress theory[J].Composite Structure,2012，8:97-110.

[12]SIMSEK M,OCATURK T K,AKBAS S D.Static bending of a functionally graded microscale Timoshenko beam based on the modified couple stress theory.Composite Structures,2013，95(1):740-747.

[13]ANSARI R,FAGHIH M ,GHOLAMI S R,et al.Thermal postbuckling behavior of size-dependent functionally graded Timoshenko microbeams[J].International Journal of Non-Linear Mechani-cs,2013,50(50):127-135.

[14]CHEN W J,MA X,LI L.A model of composite laminated Reddy plate based on a new modified couple stress theory[J].Composite Structures,2012,94(7):2143-2156.

[15]CHEN W J,CHEN W W,SZE K Y.A model of composite laminate Reddy beam based on a modified couple stress theory[J].Composite Structures,2012,94(8):2599-2609.

[16]CHEN W J,LI X P.Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory[J].Arch Appl Mech,2012,83(3):431-444.

[17]CHEN W J,SI J L.A model of composite laminated beam based on the global-local theory andnew modified couple stress theory[J].Composite Structures,2013,103(3):99-107.

(责任编辑：宋丽萍英文审校：隋华)

Thermal size effect of laminated composite plate based on Reddy-type modified couple stress theory

WU Qiong,WU Zhen

(Key Laboratory of Liaoning Province for Composite Structural Analysis of Aircraft and Simulation,Shenyang Aerospace University,Shenyang 110136,China)

Abstract：By introducing material length scale parameter of fiber and matrix,a Reddy-type modified couple stress theory is developed to analyze the thermal size effect of composite laminated plate.In the proposed model,the rotation vectors are considered as independent variables,and curvature tensor is asymmetric.However,this model is still adaptable to the isotropic material.By considering thermal strain induced by temperature in X-axis and Y-axis,the thermal bending of simply-supported plate is analyzed by using the Reddy-type modified couple stress model.Numerical results show that the size effect of material has to be considered for the thermal bending of laminated composite micro-plate.

Key words：Reddy-type modified couple stress theory;laminated composite plate;thermal bending;size effect

doi:10.3969/j.issn.2095-1248.2016.01.003

中图分类号：TP391.7; V261.2

文献标志码：A

文章编号：2095-1248(2016)01-0013-05

作者简介：吴穹(1990-)，男，辽宁沈阳人，硕士研究生，主要研究方向：多层度层合板热分析，E-mail:705180054@qq.com；吴振(1977-)男，黑龙江佳木斯人，博士，教授，博士生导师，主要研究方向：复合材料力学研究，E-mail: wuzhenhk@163.com。

基金项目：国家自然科学基金(项目编号：11272217)

收稿日期：2015-03-10