基于裂缝模拟的悬臂梁结构健康监测研究

那 磊

煤炭工业规划设计研究院有限公司 北京 100120

1 前言

结构健康监测是一个监测结构损伤的过程，这一过程是利用传感器采集结构动态响应数据来观察结构状态，从收集到的数据中提取出结构损伤的特征，进而，结构当前健康状况可以通过对该特征分析来确定。由于结构损伤引起的结构特性变化对结构动力性能有影响，因此可以通过量化结构动力特性的变化来对结构损伤进行识别。此外，利用结构振动测试方法可以有效监测结构损伤。根据结构健康监测理论，结构特征的变化会引起模型监测数据参数的变化。

目前已有大量的研究利用理论计算对不同梁的固有频率进行计算。本文旨在研究和分析线性和弹性悬臂梁的一阶和二阶固有频率衰减与不同裂缝位置、宽度和高度之间的关系，利用有限元分析软件ANSYS对不同裂缝参数引起的两个固有频率进行计算分析。进而，利用计算结果和相应变化关系作为基本数据库，为今后评估裂缝位置和尺寸提供数据支持和理论依据，达到结构健康监测的目的。

2 建模分析及结果分析

2.1 模型建立及模态分析

结构健康监测概念和理论研究需要依靠一个合理的研究系统。基于振动的结构健康监测原理，本文设立一根一端固定一端自由的等截面矩形截面钢悬臂梁模型，该梁长2m，宽0.2m，高0.2m，本次模拟为线性系统且处于弹性形变。该梁的弹性模量为2.068×1011 N/m，泊松比为0.33，容重为7850kg/m3。此外，建立一个有裂缝的悬臂梁模型，裂缝在靠近支座处的梁上表面。在模型中逐渐调整裂缝的位置、宽度和高度，以调查确定梁的固有频率是否随着不同裂缝参数改变。实际工程中，裂缝的几何结构相对较复杂，为方便模拟，本文对裂缝形状进行相应简化处理。不同荷载引起的裂缝形状基本为倒三角形，靠近支座处倒三角一侧呈垂直状，但在实际模拟中倒三角裂缝存在网格划分问题，很难控制斜边附近单元的网格密度。因此，将用等效矩形裂缝代替模拟真实倒三角裂缝形状。这里用L表示裂缝与悬臂梁支座距离，W表示裂缝宽度，D表示裂缝高度。在模型中模拟裂缝的基本原理和途径是局部刚度削弱，通过削弱裂缝处一个或一些单元的刚度来实现裂缝的模拟。

利用有限元分析软件ANSYS对悬臂梁的裂缝进行模拟时，将采用PLANE 182单元代替BEAM 3单元，且将该悬臂梁模型视为二维模型。在ANSYS软件中快速建立悬臂梁模型时，首先选择相应的单元类型和是常数；其次建立材料模型，本项目中材料模型是弹性的和线性各向同性的；最后用关键点表示悬臂梁矩形截面的顶点。在此基础上，削弱需要出现的裂缝位置处的单元刚度，实现裂缝的模拟。

2.2 ANSYS分析结果的收敛判别

2.2.1 无裂缝梁固有频率的收敛判别

为了比较裂缝出现前后悬臂梁的固有频率的变化，首先需要有无裂缝梁的固有频率。在ANSYS软件中，根据前一节所述的有限元分析方法，对模型进行网格划分，进而分析出固有频率值。然而，由于网格划分密度没有标准的判定标准，因此需要借助收敛判别方式。从有限元分析的观点来看，系统单元越离散，结果就越准确。但是，当网格划分密度到达一定临界值后，结果的变化会越来越小，可以忽略不计。因此，为了完成无裂缝梁固有频率的收敛判别，首先设定网格尺寸为0.1×0.1m，得到前两阶固有频率，随后逐渐减小网格尺寸至最小尺寸为0.005×0.005m，得到相应的前两阶固有频率值，见表2.1。

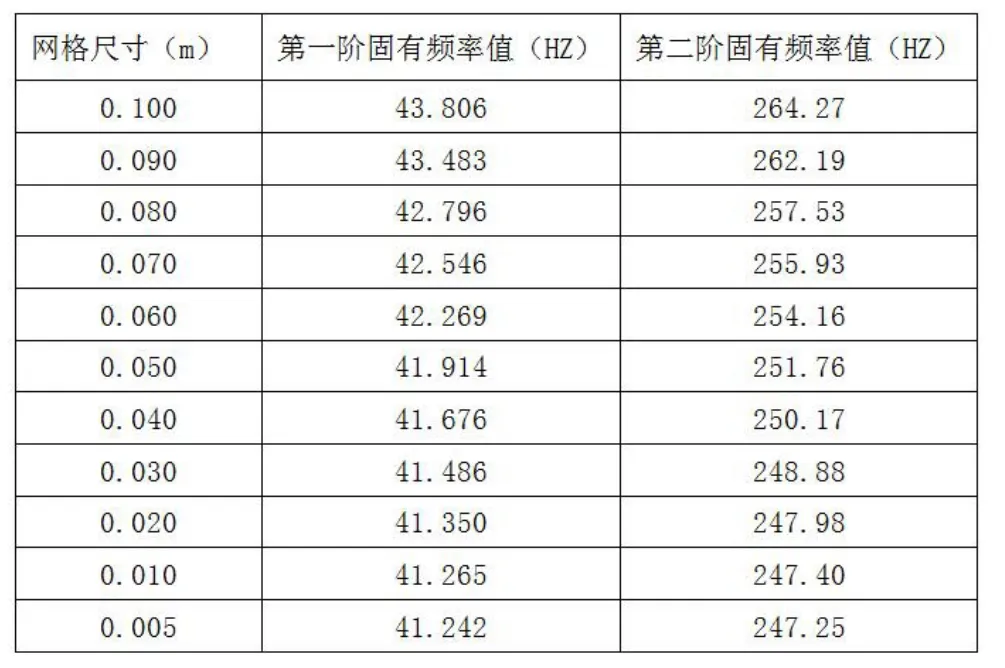
表2 .1 不同网格尺寸情况下无裂缝梁前两阶固有频率

图2 .1 无裂缝梁第一阶和第二阶固有频率收敛

从图2.1可看出前两阶固有频率随着网格尺寸划分不同而变化，在初始阶段，当网格尺寸较大时，前两阶固有频率的变化相对较明显，然而随着网格尺寸越来越小，在相应位置图形切线的斜率逐渐减小并趋近于零，图形收敛到水平渐近线。换言之，这时固有频率的减小量可忽略不计。因此，无裂缝梁的前两阶固有频率值分别为41.265Hz和247.40Hz。

2.2.2 有裂缝梁固有频率的收敛判别

悬臂梁的裂缝形式种类繁多，包括不同的裂缝位置、裂缝宽度和高度，也将对应不同的第一与第二阶固有频率。选取几个典型的裂缝参数进行相应的固有频率收敛判别，若选取的裂缝参数对应的临界网格尺寸相同，则可判定该网格尺寸可适用于其他不同裂缝参数。本节选取以下三种裂缝参数进行分析研究:（1）悬臂梁裂缝参数：位置L为0.040m，宽度W为0.010m，高度为0.020m；（2）悬臂梁裂缝参数：位置L为1.000m，宽度W为0.025m，高度为0.100m；（3）悬臂梁裂缝参数：位置L为1.800m，宽度W为0.050m，高度为0.050m。采用上述裂缝参数，利用ANSYS软件分析对应的第一与第二阶固有频率，结果见表2.2。

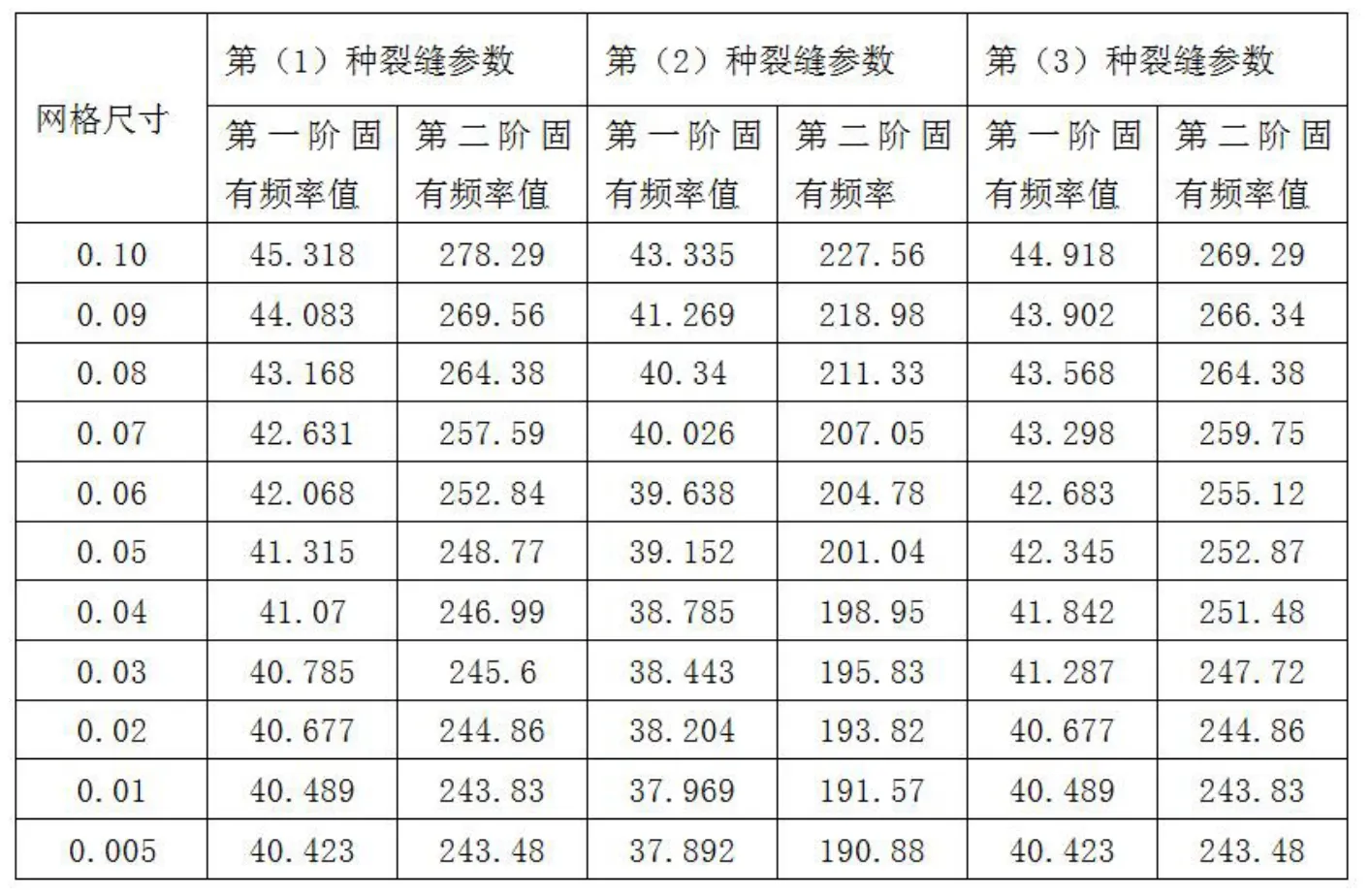
表2 .2 三种裂缝参数情况下第一阶和第二阶固有频率

根据表格显示，无论采用那种裂缝参数，前两阶固有频率的变化趋势大致相同，且三种裂缝参数下两个固有频率的临界网格尺寸均为0.01m。因此，从逻辑上可推断出任何裂缝的临界网格尺寸应为0.01m。

2.3 固有频率与裂缝位置、宽度及高度变化的关系

本节在设置裂缝的位置、宽度或高度为唯一变量的情况下，利用ANSYS软件计算分析出相应的固有频率值，各唯一变量的设置及对应固有频率值详见表2.3。通过结算结果可以分析并建立各唯一变量与前两阶固有频率间的变化关系图（此处省略图表），不难发现，裂缝宽度和高度越大，前两阶固有频率越小，而裂缝离支座端越远，第一阶固有频率越大，第二阶固有频率则呈正弦波型，在0.5m和1.9m处为波峰，在0.05m和1.0m处为波谷。

表2 .3 不同裂缝参数对应的第一与第二阶固有频率值

为更直观的表达裂缝出现前后固有频率的变化，通过引入固有频率折减的概念（即出现裂缝后与出现裂缝前的固有频率比值），依据上述分析结果，可建立单一裂缝变量与固有频率折减的关系。另外，为方便表达，定义一些符号，例如分别为裂缝距离（L）为单一变量时裂缝出现后、裂缝出现前第一阶固有频率值，其余符号定义规则类同。根据ANSYS计算结果，绘制出关系图见图2.2～2.4。结果表明，随着裂缝位置与支座端距离的增大，第一阶固有频率折减增大，此外，第二阶固有频率折减的变化呈正弦波形，但与之不同的是在第二个波谷后折减量不再减小；裂缝宽度增大与第一阶、第二阶固有频率折减均呈线性关系，而第二阶固有频率的折减比第一阶要小，折减变化率也低；而随着裂缝高度增大，第一阶固有频率折减变化趋势呈类抛物线状，且折减变化率越来越大，第二阶固有频率折减与裂缝高度变化的关系基本呈直线，有类抛物线的趋势。

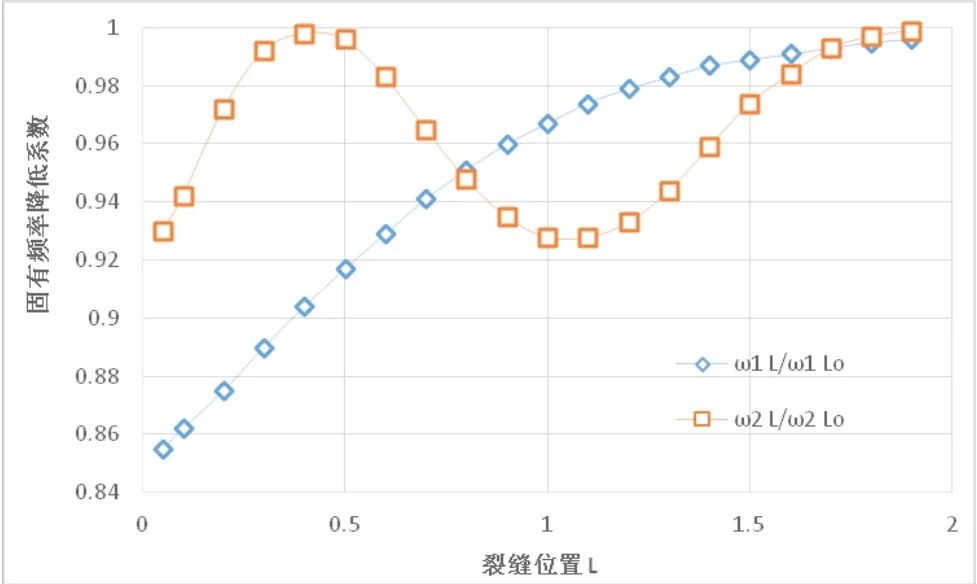
图2 .2 裂缝位置变化与固有频率折减的关系

图2 .3 裂缝宽度变化与固有频率折减的关系

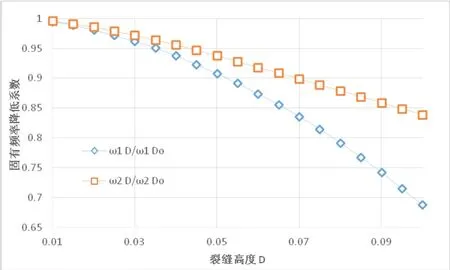
图2 .4 裂缝高度变化与固有频率折减的关系

此外，在分析单一裂缝参数变量与固有频率折减的关系的基础上，为更全面地反映不同裂缝对固有频率折减的影响，可以延展至两种裂缝参数共同变化对固有频率折减的影响（此处忽略图表）。经过分析，当裂缝宽度和高度同时增加时，固有频率均会折减，但第一阶固有频率折减程度较第二阶更大，换言之，相同的裂缝参数下，第一阶固有频率折减较第二阶更严重。另外，随着裂缝高度的增加，裂缝宽度相对较大的梁第一阶和第二阶固有频率的折减速度高于裂缝宽度较小的梁。但是研究发现，相对于裂缝宽度较大的梁，裂缝宽度较小的梁的第二阶固有频率折减量明显较大。除此之外，对于任何裂缝宽度和高度，随着裂缝距离支座端的距离增加，第一阶固有频率均会减小，然而第二阶固有频率不会随裂缝距支座端的距离增大而连续减小。综上所述，当裂缝位置确定时，第一阶和第二阶固有频率的变化足以用来进行裂缝宽度和高度的识别，然而由于固有频率变化的随机性，还不足以对裂缝位置进行估计和识别。因此，未来的研究可致力于评估不同裂缝位置损伤结构的前三阶或更多固有频率上，用更多的结构特性参数数据支撑结构健康监测体系。

4 小结

本文中提到的分析过程为结构健康监测的逆程序，该程序为利用所提供的裂缝位置、宽度和高度评估结构的固有频率，从而可根据裂缝梁的固有频率值评估裂缝的位置、宽度和高度，进行反向推导。该程序可推广并应用在结构健康监测中。然而，这个方法有一定局限性，第一裂缝位置在现有研究数据中很难评估，第二由于ANSYS软件网格划分的操作误差，在裂缝相对较小的情况下固有频率的变化很难准确量化。这些问题是我们今后研究的重点。