精心设计课堂练习 努力打造高效课堂

福建武夷山市崇安小学（354300）彭娟华



精心设计课堂练习努力打造高效课堂

福建武夷山市崇安小学（354300）彭娟华

［摘要］根据儿童的认知规律，精心设计课堂有效练习，打造出高效的数学课堂。精心设计简约的练习，让练习内容丰富；精心设计有趣的练习，让练习充满活力；精心设计综合性的练习，让练习彰显成效；精心设计阶梯性的练习，让练习彰显时效；精心设计实践性的练习，让练习凸显数学的价值；精心设计留白练习，让练习彰显精彩。

［关键词］设计高效课堂练习

随着课程标准的实施，有效教学理念已渗透到教学的各个方面，如何精心设计课堂练习，打造高效课堂是教师面临的问题。随着我校《小学数学课堂教学中练习设计的有效性策略研究》课题的开展，我们组织了教研活动、教学沙龙、听常态课、学生问卷等实践活动。随着一系列实践活动的完成，数学课堂练习设计的盲目性和随意性问题日益突显，归纳起来有以下四方面：（1）练习的设计没有目的，常常是重复单调，杂乱无章的；（2）多是“一刀切”，没有层次性的练习；（3）侧重书面练习，很少创造出符合学生生活实际的练习；（4）重视技能训练，忽视思维能力的培养。

针对以上存在的问题，结合教学实践，我认为：在教学中，教师必须要认真钻研教材，把握教材的知识结构，挖掘教材的潜在知识点，根据儿童的认知规律，精心设计有效的课堂练习，打造出高效的数学课堂。

一、精心设计简约的练习，让练习丰盈内涵

莎士比亚说：“精练是智慧的灵魂。”为了能够解放学生的双手和大脑，让他们能轻松愉悦地学习，不被题海所淹没，教师就要根据教学内容和本班学生的实际情况，精心设计出简约的课堂练习，即有针对性、递进性、综合性的题目，尽量做到一题多解，一题多用，一题多变，力求达到在简约中求多变的效果。

例如，在教学“平行四边形的面积”时，我设计了一道题：

（1）小区内有一个平行四边形的花圃，你能求出它的面积吗？

（2）求出边长为5m的这条边所对应的高。

（3）这道题的第（1）、第（2）问有什么共同的地方，又有什么不同的地方？如果小区物业要给这块平行四边形的花圃重新铺上草坪，每平方米需要6元，铺这块地一共需要多少元？如果要在这个花圃里种月季花，每4平方米种一株，一共可以种多少株？

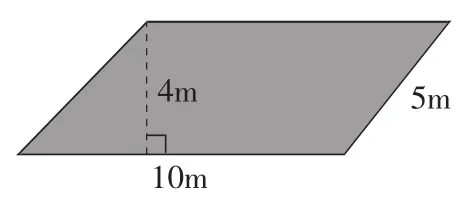
本节课的第一个学习目标是让学生灵活运用平行四边形的一组相对应的底和高计算平行四边形的面积。如图所示，已知一组相对应的底和高，学生通过审题和思考，很快就能求出第（1）问。第二个学习目标是让学生能根据已知的两个量求第三个量，并能解决简单的实际问题。对于第（2）问，根据已知条件，能求出平行四边形的面积，再通过题中给的另一底边的长，求出对应的高。第（3）问让学生反思：这道题的第（1）、第（2）问有什么共同的地方，又有什么不同的地方？

可见，围绕教学目标，设计不同层次的练习，并将数学知识放在具体的问题情境中，既能激发学生的求知欲望，也能培养学生解决实际问题的能力。

二、精心设计有趣的练习，让练习充满活力

数学源于生活，又用于生活。由于小学生天性好玩、好动，因此在结课阶段，学生的积极性减弱，注意力也不够集中。这时内容枯燥、形式单一的练习会使学生产生厌烦情绪，而富有创意，形式新颖，并有一定趣味性的练习，才能使学生情绪高涨，把“要我学”的心态调整为“我要学”。

例如在教学“2、3、5的倍数”时，我在课堂上设计这样的练习：放一把豆子在桌子上，让学生用自己喜欢的方法数一数。几分钟后，我问：“豆子数完了吗，说说你们是用什么方法数的。”生1：“老师，我认为2个2个地数又快又对。”“不对。”生2站起来说，“5个5个地数更快。”教室里顿时热闹起来：“2个2个地数更快”“5个5个地数更快”，两种声音此起彼伏。这时，我又抛出一个问题：“有没有人认为3个3个地数又快又对的？”生3说：“3个3个地数不好数，容易出错。”我趁机再问：“为什么会觉得2个2个或5个5个地数又对又快，而3个3个地数却不容易呢？”学生陷入了沉思，忽然生4站起来说：“2和5的倍数，个位上都有特征，我们好记、也好数，可3的倍数个位上没有特征，我们不容易数。”大家听完都不约而同地鼓起掌来。

在这里，数豆子的方法把枯燥的练习变得有趣，课堂变得特别活跃。

三、精心设计综合性的练习，让练习彰显成效

小学生学习数学，往往会产生思维定式，学习了分数乘法应用题，所有的题目都用乘法做，学习了分数除法应用题，所有的题目就用除法做。然而当不同类型的问题综合在一起时，学生就手足无措了。因此，练习的设计要考虑与前后知识相互联系，瞻前顾后，做到新旧知识不断交替出现，使学生能把掌握的新知识纳入已有的知识体系，又能让旧知识得到巩固，不断提高学生的综合能力。

例如，学习“分数除法”后，学生做题时往往不分析条件，就直接用数量除以分数得出总量。因此，我设计了两道题：

为了让学生在比较、分析中找到分数乘法应用题与除法应用题的异同，加深理解，我运用画线段图和寻找等量关系的方法给学生讲解，达到了理想的学习效果。因此设计练习时，就要设计一些对比性强的练习，让学生辨别、分析、比较，找出异同点，加深认识，使知识达到内化的程度。

四、精心设计阶梯性的练习，让练习彰显时效

在设计练习题时，不仅要考虑教学内容，而且要考虑学生的知识水平、认知能力与生活实际。不但要有基础训练，还要设计综合型的、拓展型的题目。这样，后进生能巩固基础，中等生不断提高，优等生综合能力更强，所有的学生都得到不同的发展，体现出练习的最佳效果。

例如在教学“圆的面积”时，我设计了以下练习：

（一）判断。

1．圆的半径越长，圆的面积就越大。（）

2．周长相等的两个圆，面积也一定相等。（）

（二）只列式不计算。

1．半径是3分米，求圆的面积。

2．直径是8分米，求圆的面积。

3．周长是12．56米，求圆的面积。

（三）解决问题。

1．一个圆形旱冰场的直径是30米，扩建后，半径增加5米。扩建后的旱冰场的面积比原来增加了多少平方米？

2．在一个长8厘米、宽6厘米的长方形纸里剪下一个最大的半圆，这个半圆的面积是多少平方厘米？

通过这几个类型不同、难度逐层递进的练习，学生加深了对圆面积的理解，掌握了圆面积的计算公式，增加了综合运用所学知识解决实际问题的能力，从而对数学学习更有信心，更加积极主动。

五、精心设计实践性的练习，让练习凸显数学的价值

设计练习不应只停留在巩固知识上，更重要的是要让学生学以致用，给学生提供实践活动的机会，培养学生乐于动手、勤于实践的意识和习惯。

实践性作业主要有：（1）动手操作型。教学“圆的面积”一课后，我设计了一道练习题：一张长15厘米，宽10厘米的长方形卡纸，用来剪裁直径是4厘米的圆形，最多能剪几个？我让学生先动手在本子上画一画，试试能画几个，再让学生拿出纸张来剪一剪。通过动手操作，避免了学生用长方形的面积除以圆的面积来解题的错误。（2）调查整理型。如调查家中的各项开支情况，或是调查一分钟内学校门口经过的车辆，再从调查得到的信息中进行整理与分析，想想从中得到哪些数学信息，可以提出哪些数学问题。（3）研究记录型。鼓励学生把自己在生活中发现的数学问题用写日记或手抄报的形式记下来。

小学生的思维以具体形象思维为主，数学教学中要多让学生动手操作，发挥小学生形象思维的优势，实现课堂教学目标。

六、精心设计留白练习，让练习彰显精彩

教师要适量地设计课堂练习，必要时可适当留白。留白是教师在某些环节留一定的悬念，让学生去探索、体验、思考和解答。巧妙的留白，能起到无声胜有声、言已尽而意无穷的效果。

例如教学“三角形的内角和”时，学生验证了三角形的内角和是180°，并能应用其解决实际问题后，我让学生听着音乐，感受不同的“三角形的内角和是180°”的验证方法，并让学生再想想还有什么问题？这时一个学生问：“老师，四边形的内角和是多少度呢？”另一个学生很快答道：“长方形和正方形四个角都是直角，四个直角加起来是360°，长方形和正方形也是四边形，所以说四边形的内角和应该是360°。”于是我说：“你能用这种方法分析得出四边形的内角和是360°，真不错！还能在本子上画一些非特殊的四边形进一步验证吗？”学生经探究和讨论后得出：把一个四边形分成两个三角形，由于每个三角形的内角和是180°，所以四边形的内角和是360°。接下来学生在操作、分析、讨论中，还得出了五边形、六边形等内角和的特征，把整节课推向了高潮。

虽然教师在备课时不能预见课堂上的所有细节，但是留有一定的“空白”，引导学生进行思考，会得到许多意想不到的惊喜，课堂教学也会充满活力并彰显别样的精彩。

设计练习是一门学问，需要我们不断探索和改进教学方法，做到“少、精、活”。总之，只要我们精心设计有效的课堂练习，让学生既尝到成功的喜悦，又受到错误的警醒；既学得生动，又学得扎实；既发展思维，又培养能力，就是最高效的数学课堂。

（责编莫秋鸿）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）01-058