浅谈《几何画板》在初中数学教学中的应用

沈琦

【摘要】 初中数学教学的最大难点，莫过于函数和几何这两大板块，其概念的抽象以及动态的变化过程，都给教师的教学、学生的学习，带来了很大的困难.因此，运用信息技术辅助教学，引起了越来越多教师的重视.在众多的教学软件中，《几何画板》因其图形编辑方面的优势，受到许多教师的喜爱.运用《几何画板》，能更好地激发学生学习的热情，切实有效地提高课堂教学的效率.

【关键词】 几何画板；初中数学教学；二次函数；变式教学

数学课程标准指出：教师要充分考虑信息技术对数学学习内容和方式的影响，开发并向学生提供丰富的学习资源，把现代信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式，使学生乐意并有可能投入到现实地、探索性地数学活动中去.就数学学科而言，尤其是几何以及涉及图像的函数教学，《几何画板》具有不可替代的优越性.下面，笔者结合自己在教学中的例子，谈一点体会.

一、利用《几何画板》研究二次函数y = ax2及y = a（x + m）2的平移

二次函数的平移，是对数形结合思想的集中体现，传统的教学方法中，教师会引导学生先将y = ax2及y = a（x + m）2的图像画出，然后逐一进行类比，通过观察它们的异同，寻找其中的变化规律.这种教学方法的弊端是：

① 要作多个函数的图像，课堂效率较低；且对函数性质的认识受限于图像是否画得足够规范；

② 无法有效地从运动的观点来揭示问题的本质，学生往往一知半解，容易形成教师的“一言堂”.尤其是对图像平移“左加右减”这一规律的认识，往往容易与坐标平移“左减右加”相互混淆，教学效果不佳.

利用《几何画板》，可以有效解决这些问题，以下是笔者上课的片段：

片段1：利用《几何画板》研究抛物线y = x2，y=（x + 2）2以及y = （x - 2）2之间的关系.

第一步：利用“绘图”菜单下的“定义坐标系”功能建立平面直角坐标系，再利用“绘制新函数”功能构造任意直线（如直线y = -2）；

第二步：在平面直角坐标系中绘制以下三点A（-2，-2）、B（2，-2）、C（0，-2），以及在直线y = -2上的任意一点M，度量出点M的横坐标XM；

第三步：依次在坐标系中，绘制二次函数y = （x + xm）2，y = （x + 2）2以及y = （x - 2）2的图像；

第四步：依次选中M点和A点，利用“编辑”菜单下“操作类按钮”构造“移动”按钮，将其改名为“右移”；依次选中M点和B点，构造“左移”按钮；选中M点和C点，构造“还原”按钮.（如图1）

此时，教师通过对“左移”、“右移”、“还原”三个按钮的控制，提出以下问题：

师：在平移的过程中，抛物线的什么不变？什么发生了改变？

生1：开口方向不变.

生2：顶点坐标和对称轴发生了改变.

师：抛物线y = （x + 2）2的顶点坐标和对称轴分别是什么？

生3：顶点坐标是（-2，0），对称轴是直线x = -2.

师：抛物线y = x2向哪个方向平移多少个单位，可以得到抛物线y = （x - 2）2？

生：向右平移2个单位.

紧接着，我与学生一起概括了抛物线y = a（x + m）2的性质，以及它与抛物线y = ax2的关系.通过对这一动态过程的观察，学生很容易地得出m的值对整个平移过程中的影响，直观明了，易于理解，也就印象深刻.

二、利用《几何画板》进行变式教学

初中数学提倡变式教学，教师通常在保持教学内容核心本质不变的前提下，改变其外在的某些属性，引导学生从不同的角度去换位思考，从而更准确的认识所学知识点的本质和内涵.以图形教学为例，教师可以从变换问题的条件和结论，或者对图形作间隔、缺损、重叠、交错等方式的处理，来达到变式教学的目的.

在传统的课堂中，教师为了进行变式教学，往往需要耗费许多宝贵的时间来大量地板书作图，而画出来的图形有时不够准确，又都是静态的，容易掩盖一些内在规律，也就很难真正引起学生主动探究的欲望，教学效果大打折扣.

《几何画板》作为一种专门研究动态几何的教学软件，在这方面有着明显的优势.下面是笔者关于《三角形的中位线》一课中的一道课本练习题的教学过程.

片段2：首先，教师利用几何画板，出示原题以及相关图形.（如图1）

求证：顺次连接四边形四条边的中点，所得的四边形是平行四边形.

并引导学生通过联结四边形对角线，利用三角形中位线定理完成证明.

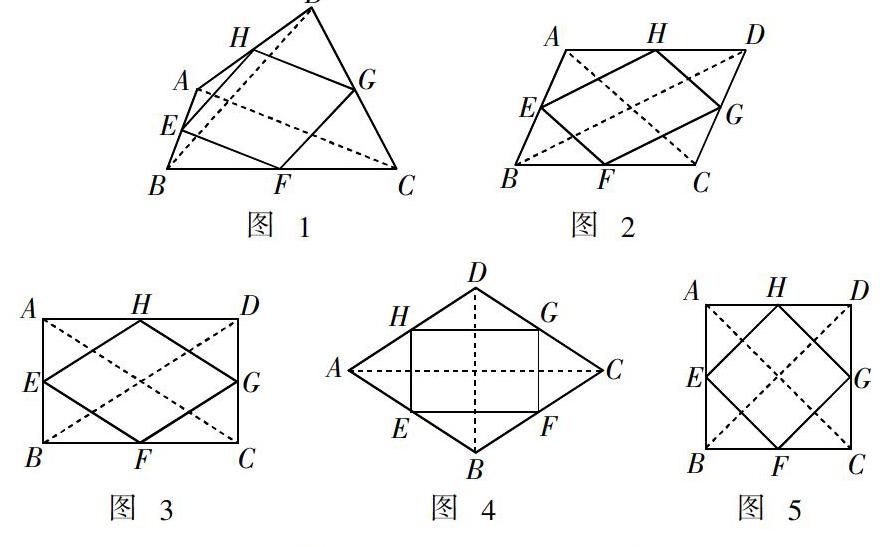
接下来，开始进行变式教学：（如图2～5）

变式一：若四边形ABCD是平行四边形，则四边形EFGH是什么形状的图形？

变式二：若四边形ABCD是矩形，则四边形EFGH是什么形状的图形？

变式三：若四边形ABCD是菱形，则四边形EFGH是什么形状的图形？

变式四：若四边形ABCD是正方形，则四边形EFGH是什么形状的图形？

此时教师进一步提问：四边形EFGH的形状与四边形ABCD的什么因素有关？并运用几何画板不断变换四边形ABCD的形状，只保持对角线相等或垂直.从而总结得出：四边形EFGH的形状是由四边形ABCD对角线的关系所决定的.

在这节课的教学过程中，教师事先利用《几何画板》制作好教学课件，将问题逐一展示，不断深入挖掘问题的本质，《几何画板》处理信息量大、图形显示鲜明准确的优点得到了淋漓尽致的体现.

在以上两个例子中，充分体现了运用《几何画板》辅助教学的两个优势：

1. 培养学习兴趣，提高教学效率

美国教育家布卢姆早就说过：学习的最大动力，是对学习材料的兴趣.有时，总是有些无法入门的感觉，久而久之，还容易产生畏惧心理，究其原因，首先是这部分内容过于抽象，不易理解.其次，在学习方式上，它与其他内容也有很大的不同，一味地埋头计算是很难学好的.尤其是函数的性质，死记硬背往往容易将几个函数的性质混淆在一起.事实上，教材在处理函数性质时，知识的建构也始终是围绕图形来展开的.在探究函数性质的过程中，需要学生和老师一起，绘制大量的图形，然而利用黑板的传统教学中，基本只能处理静态的函数图像，无法将运动的过程演示出来.学生在学习时，往往只能依靠自己的抽象思维，一旦无法透彻理解，就只能将老师讲的结论强行记住，教学效果自然不佳.通过使用《几何画板》，既可以让教师节省大量的绘图时间，又能动态的展示函数图像的形成以及变化过程.教师还可以将几个函数的图像事先画在一个屏幕上，引导学生对这些图形进行对比和分析，教学效率的提升是显而易见的.如果条件允许，教师还可以教学生操作《几何画板》的基本方法，引导学生自主探究一些课本中的简单问题.从而更能激发学生学习的热情，有助于发挥学生的主体性、积极性和创造性.在这个过程中，学生能更深切地认识到，数与形相结合，才是学好函数的最重要的途径.

2. 深入变式教学，扩大课堂容量

新课改的不断深入，告诉我们要注重培养学生应变能力，创新能力.而“变式教学”是实现这一目标的有效途径之一.通过“变式教学”，一题多变，一题多解，使学生对原先陈旧的问题产生一种新鲜感，从而产生浓厚的学习兴趣，更好地参与到课堂学习中去.几何的变式教学中，往往需要对现有的图形作出各种改变，无论是时间还是空间上，都会加大教师教学的难度.使用《几何画板》，教师可以轻易地解决这个难题.教师可以事先利用《几何画板》画好图形，然后根据教学设计的需要，随意改变原题的题设和结论，同时改变图形的结构，而不必重新再画图形.在进行问题的小结时，还可以将之前出现的各种情况一并展示给学生，从而使学生对问题本质的把握更加深刻.

华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”.《几何画板》在教学中的使用，能有效地将抽象的数学知识形象化，扩大知识的内涵，丰富教师讲课的方式，减轻学生学习的困难.利用《几何画板》，更能提高学生对学习的兴趣，培养学生善于观察、勤于总结、自主学习、探究问题的习惯.当然，作为一种辅助教师教学的工具.它也一定有其局限性.事实上，任何教学辅助软件，都不能取代教师本身在课堂中的作用.一个再好的课件，如果没有高水平的教师去驾驭它的话，充其量也不过是一个精美的图形软件而已，《几何画板》当然也无法例外.因此，教师必须处理好两者之间的平衡关系，在教学中应更加认真地专研教材，仔细备课，真正地做好课件，用好课件，发挥它最大的教学功能.