基于APOS理论的函数单调性概念教学设计

刘吉顺

摘 要：APOS是美国学者杜宾斯基提出的关于数学概念学习的学习理论，主要是在传统教学的基础上，通过APOS理论设计函数的单调性概念教学，从而制作出成熟的教学方案，为函数概念教学提供理论依据。

关键词：APOS；函数单调性；教学设计

随着教学理论的发展，诸多新颖的教学设计融入当前的教学过程中来，其中，APOS理论能够通过阶段模式多快好省地解决函数单调性等数学难题，是行之有效的教学设计方法，值得推广应用。

一、APOS的含义

APOS是美国学者杜宾斯基提出的有关数学概念学习的学习理论，其认为，学生学习数学需要经过四个阶段，即操作阶段、过程阶段、对象阶段以及图式阶段，该理论不仅表明学生的学习构建过程，还对构建层次分别说明。

操作阶段主要是促使学生明确问题概念和背景之間的关系；过程阶段主要是学生概括思考的过程，通过思维内化从而明确概念性质；对象阶段是经过明确概念本质，将其予以压缩，并且赋予形式化的符号及定义，从而演变为思维对象，从而在学习过程中创建新活动；图式阶段是在长时间学习后予以完善，刚开始的图式包括符号、定义以及特例等抽象过程，随后建立起图形、规则与其他概念的关联，从而逐渐演变成综合的心理图式。

二、函数单调性概念数学设计

（一）设计说明

作为函数章节中最重要的性质——单调性，不仅是学习的重点，更是学习的难点，由于单调性定义较为晦涩难懂，因此，对于学生而言学习并不轻松，学生认知函数单调性的困难主要包括：（1）函数图像的升降被函数符号代替，将直观转变为抽象学生并不能够完全适应，极难把握。（2）证明函数单调性必须应用单调性定义，如果对定义没有一个深刻的认识，将会致使学生在解题过程中存在诸多问题。

（二）教学过程设计

1.操作阶段

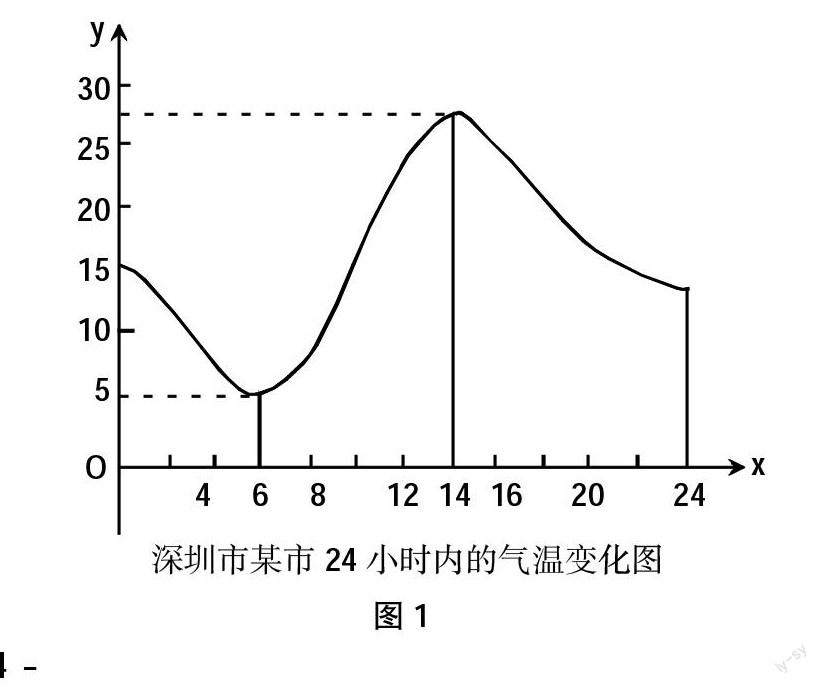
教师需要创造问题情境，对思考问题进行模拟，比如深圳某市24 h气温变化图，如图1所示：

教师需要引导学生看明图中所给的信息，并且总结信息，进行思考。

例如，教师询问：（1）该图显示哪日的温度最低？哪日的温度最高？（2）某日的某时的具体气温能否看出？（3）哪些时间段温度有上升的趋势？哪些时间段有下降的趋势？

[设计意图]通过简单的气温变化图，对函数的单调性予以简要说明，比如温度趋势对应函数的递增和递减，定位为y随着x的减小而减小以及y随着x增大而增大。

2.过程阶段

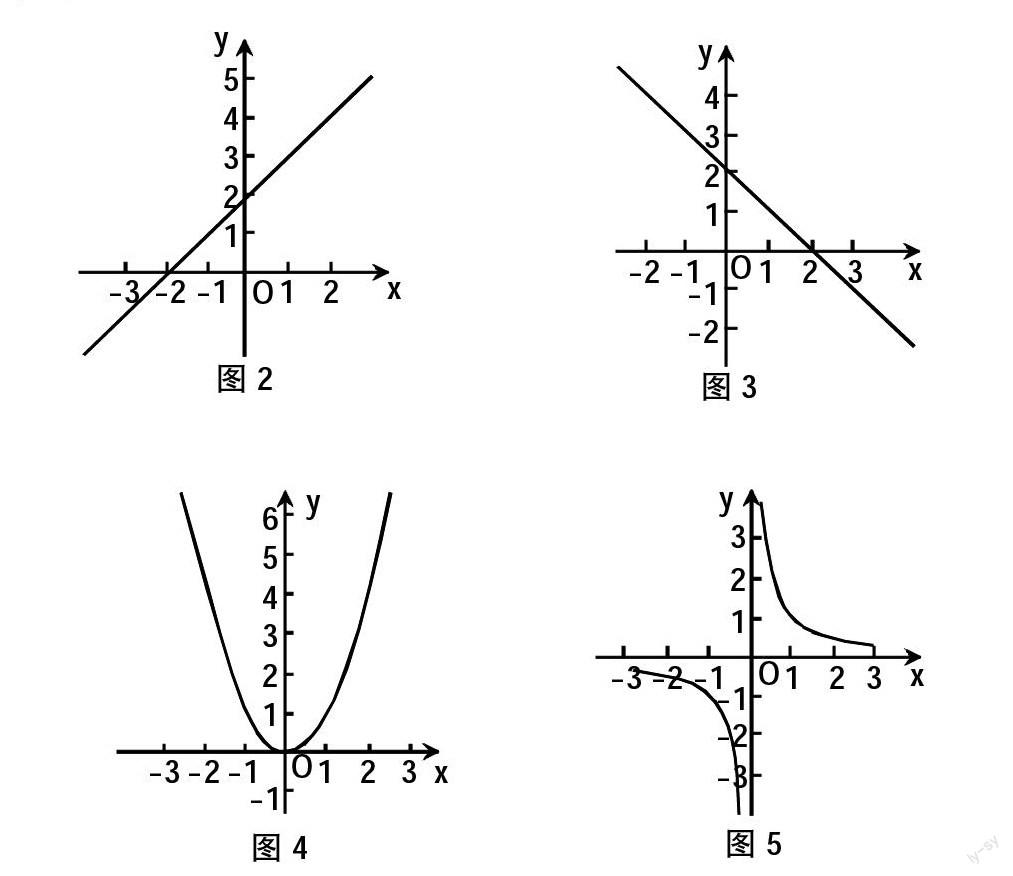
过程1：将函数y=x+2（如图2），y=-x+2（如图3），y=x2（如图4），y=（如图5），对其自变量变化过程中函数值的变化规律予以分析。

在向学生说明图像单调性过程中，必须强调是处于某个区间的单调性，从而促使学生明确单调性的局部特征，不得存在概念盲点。

过程2：用浅显易懂的话讲明增函数及减函数。

[设计意图]通过直观的表达出单调性的概念，从而实现描述性认知的目的。

过程3：直观到抽象

如何证明f（x）=x2在区间[0，∞）是增函数？

（1）任意在区间[0，∞）中取两个值，比如3和4，由于3<4，因此f（x）=x2在区间[0，∞）是增函数。

（2）根据（1）算法选取若干组予以验证，结果均满足条件，因此f（x）=x2在区间[0，∞）是增函数。

（3）选取任意数值x1，x2∈[0，∞），x2>x1，又因为x22>x12，所以

f（x）=x2在区间[0，∞）是增函数。

教师询问：怎样通过精准的数学符号对函数单调性予以定义？

师生共同探讨，从而明确增减函数的定义，并且强化学生对增减函数的理解。

[设计意图]强调自变量在区间的任意性，并且对函数加以验证，信息分析数学符号的严谨性。

3.对象阶段

判断命题真假。

（1）y=，由于f（-2）

（2）如果f（x）满足f（3）

（3）假如函数在（2，4]区间和（4，6）区间均为增函数，那么函数f（x）在区间（2，6）也为增函数。

[设计意图]通过反例的形式强调单调性定义域中存在的诸多问题。

4.图式阶段

证明函数在区间是增函数。

[设计意图]对证明函数单调性的步骤进行归纳：设元、作差、变形、断号、定论。

三、注意问题

操作阶段：在设置问题情境时需要适宜经典，确保行之有效。

过程阶段：通过思维深入引导，有针对性地升华“对象”，教师在此过程中询问“是什么”以及“为什么”“怎么样”等，并且留给学生足够的时间去思考探索。

对象阶段：对概念的本质特征深入了解，要求学生能够将概念抽象化，逐渐形成心理表象，并且加深对概念的认知和理解，在教学过程中通过反例、变式引起学生思考，并且对其不断优化

调整。

图式阶段：通过多次操作将学生“对象”层次转变为“图示”层次，并且通过多种方式促使学生理解“对象”，不能一蹴而就。

总而言之，基于APOS理论，能够有益于函数单调性的概念教学，而且能够在多学科多领域中融会贯通，值得推广应用。

参考文献：

[1]高波.基于APOS理论的职高数学概念课教学设计探析：以《函数的概念》为例[J].考试周刊，2014（11）：45-46.

[2]贺明荣.基于多元表征理论的函数单调性教学设计[J].上海中学数学，2013（12）：1-3.

[3]孟世才.基于APOS理论的中学函数概念的教学研究[J].教学与管理：理论版，2011（21）：95-96.

编辑 韩 晓