以变显质

张同刚

摘 要：在初中数学的教学过程中，变式教学是一种科学合理的教学方法。通过“变”发现数学“不变”的本质，有效提升初中数学教学质量。基于此，首先探究变式教学应遵循的原则，然后探究变式教学法在数学教学过程中的应用策略。

关键词：变式教学；初中数学；教学质量

所谓数学变式教学，主要是引导学生对多变的数学问题进行探索思考，了解其变化规律，发现其中不变的本质的一种教学方法。运用变式教学，可以起到一题多用的作用，有效增强数学知识的创新性和趣味性，充分调动学生的求知欲和好奇心，让他们能够积极主动地去学习和思考，进而掌握科学合理的分析方法。通过“变”发现数学“不变”的本质，有效提升初中数学教学质量。对此，笔者简单论述如下：

一、变式教学应遵循的原则

在初中数学教学过程中应用变式教学，为了达到预期的教学效果，则必须遵循以下几个原则：（1）题目的引申应合适有度。在初中数学的实际教学过程中，如若盲目引申题目，则会加重学生的学习负担，让其产生负面的学习情绪。因此，在初中数学变式教学中，应该根据学生的实际学情和教材内容合理引申习题例题的内容和方式，以此调动学生的学习兴趣，激发学生的学习灵感，从而有效提升学生的学习水平。（2）根据学生接受能力制订教学目标。在应用变式教学方法时，应以学生掌握基础知识和接受知识的能力为前提，制订相应合理的教学目标，这样才能够取得更好的教学效果。（3）以调动学生的主观能动性为目的。在应用变式教学法的实际过程中，主要是老师引导学生去理解“变”的知识点，让学生在“多变”的教学过程中掌握分析方法，有效提升自己的理解能力。

二、变式教学法的应用策略

（一）强化习题变式训练，引导学生总结解题思路

在初中数学知识的学习中，习题练习是非常重要的一个环节，很多数学思维方法都融于例题里面。因此，通过加强习题变式训练，能够引导学生从众多的习题中深入掌握知识点，从而总结出清晰的解题思路。其中，在所有习题练习中，填空题是较为常见的一种题型，所以可以以选择题为例进行变式教学。

例如：通过设计一个问题“将一米的绳子先截去一半，然后再将剩下的绳子截去一半，按照这样的要求，要想最后剩下的绳子不足一厘米，总共需要截多少次？”根据这个问题，可应用变式教学法转换题目：“将一根木头长设置为a米，先截去全长的，再截去剩下木头长的，问最后剩下的木头长度是多少？”通过变式教学法转换问题，不仅能够让学生快速找到解决问题的方法，而且也锻炼了学生的思维方式。

（二）合理运用正例变式和反例变式，灵活掌握数学学习法

在初中数学的学习过程中，通常例子原型及变式主要为正例变式的主要体现模式，但在运用正例变式的过程中，学生很容易将一些典型的特征错误地看成为本质特征，以致无法准确掌握概念的本质属性。除此之外，对于一些概念的例子，其本质属性都相同，但如果想准确掌握概念本质特征，仅仅从原型的标准特征入手是完全不够的。因此，在初中数学的实际教学过程中，不仅要充分运用正例变式之外，还需要灵活运用反例变式。

例如：针对“若a2=b2，则a=b。”这个命题是否正确？为了能够快速准确地得出正确的答案，老师则可指导学生从a2与a的关系入手进行判断，明确区分两者的本质特征和非本质特征，这样学生则可以轻松地举出反例。

（三）合理改变对象的存在背景，帮助学生深入了解知识点

在数学变式教学法的应用过程中，应根据对象的存在背景进行合理改变，从而帮助学生深入了解知识点。其中，对象存在背景的改变主要以关键词和相似情景的变换上。

例如：在学习双曲线和椭圆相关概念时，老师则可以指导学生准确捕捉概念里的关键变化词，再将椭圆背景和圆的背景进行合理替换，这样则有利于让学生更加深入地了解和掌握相关知识点。

（四）例题变式教学的具体应用，引导学生多角度理解知识点

在初中数学的学习过程中，其各个知识点、解题技能和方法、解题思想主要是通过例题连接在一起，所以进行例题变式教学具有很重要的作用。因此，在初中例题的教学过程中，可将相关例题进行合理变式，从而引导学生能够从多角度、多层次理解知识点。

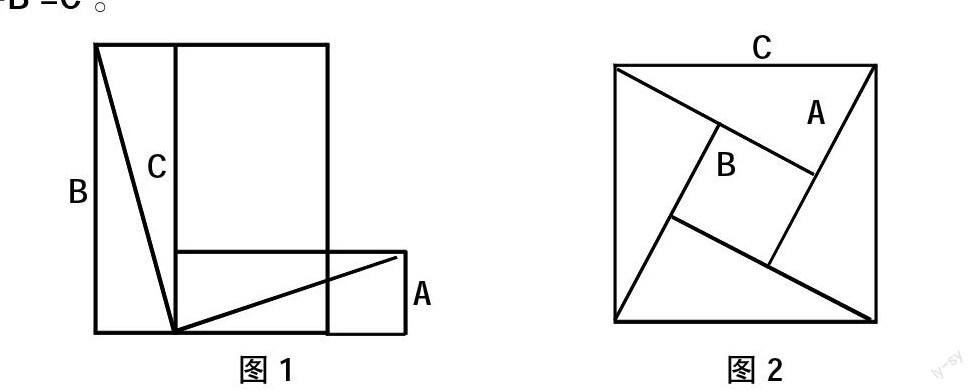
例如：在学习“勾股定理”理论时，老师可将理论融入直角三角形中，得出“两条直角边的平方和等于斜边的平方”。因此，将直角三角形的两直角边的长分别设置为A、B，斜边边长为C，求解出A2+B2=C2。

在上面的图中，其图1主要是边长为A、B的两个正方形连接在一起，S=A2+B2；而图2则主要是由4个全等直角三角形和1个小正方形组成，如若将其中两个三角形移动到图2中，则可以得到一个边长为C的正方形，所以得出A2+B2=C2，从而得出勾股定理的结论。

综上所述，初中数学变式教学法只是简单地改变问题的形式，而并没有改变问题的本质，且能够使问题更加清晰明确地呈现出来，从而帮助学生深入理解数学知识点，从本质上看待数学问题，进而培养学生敏捷的數学思维。因此，在初中数学的实际教学过程中，老师应该有意识地引导学生从“变”的现象中发现“不变”的本质，提高学生的学习效率。

参考文献：

[1]王朝晖.初中数学教学中变式教学的应用探讨[J].数学学习与研究：教研版，2015（04）：38.

[2]宋旭.浅谈初中数学发散思维与变式教学的策略[J].俪人：教师，2015（12）：340.

编辑 谢尾合