一道高等代数考题的命题思路及分析

谢启鸿

(复旦大学数学科学学院，上海200433)



一道高等代数考题的命题思路及分析

谢启鸿

(复旦大学数学科学学院，上海200433)

[摘要]给出了复旦大学数学科学学院2013-2014学年第二学期高等代数II期末考试一道压轴题的命题思路及分析.

[关键词]实对称阵； 半正定矩阵； 特征值； 反交换性

复旦大学数学科学学院代数组在每学期高等代数期末考试的命题过程中， 特别是在最后两道压轴题的命题方面， 首先一直坚持自主创新命题， 决不滥用陈题; 其次着重考察学生对高等代数最核心内容的理解与掌握， 并在解题技巧的运用方面保持一定的难度; 最后命题具有某种开放性， 能激发学生综合运用各种知识点进行解答， 形成一题多解的局面. 本文将以复旦大学数学科学学院2013-2014学年第二学期高等代数II期末考试一道压轴题为例， 详细阐述其命题思路及分析.

笔者认为高等代数II最核心的内容， 从几何的角度来看应该是内积空间理论， 从代数的角度来看应该是矩阵的正定性理论以及实正规阵的正交相似标准形理论. 因此， 高等代数II期末考试的最后两道压轴题应该在这一范围内命题. 在开始具体的命题探索之前， 我们还将遵循以下三个出发点.

出发点1相抵标准形、相似标准形和合同标准形是处理矩阵问题的重要工具. 若给定的矩阵问题在相抵、相似或合同关系下具有某种不变性， 则可以把问题化为其中一个或几个矩阵是标准形的情形进行讨论. 下面将通过两道例题来说明上述化简问题的技巧， 我们的第一个出发点是希望考察学生对这一技巧的掌握和运用.

例1设A，B，C分别是m×m，n×n，m×n矩阵， 满足AC=CB且C的秩为r. 求证: A和B至少有r个相同的特征值.

证设P为m阶非异阵， Q为n阶非异阵， 使得

为相抵标准形. 在等式AC=CB的两边同时左乘P， 右乘Q可得

(PAP-1)(PCQ)=(PCQ)(Q-1BQ).

(1)

因为相似矩阵有相同的特征值， 故由 (1) 式不妨一开始就假设C是相抵标准形

设

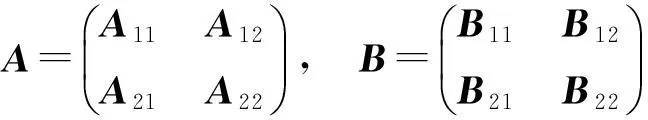
为相应的分块， 代入AC=CB可得

即有A11=B11， A21=O， B12=O. 因此

例2设A，B是n阶方阵且满足AB=BA=O， rank(A)=rank(A2)， 求证:

rank(A+B)=rank(A)+rank(B).

证设P为n阶非异阵， 使得P-1AP为Jordan标准形. 在等式AB=BA=O的两边同时左乘P-1， 右乘P可得

(P-1AP)(P-1BP)=(P-1BP)(P-1AP)=O.

同理可证对A，B同时作相似变换也不改变秩的条件和结论， 故不妨一开始就假设A是Jordan标准形. 由rank(A)=rank(A2)知A的关于零特征值的Jordan块都是1阶的， 故可设

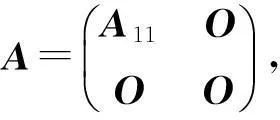
其中A11是非异阵. 设

为相应的分块， 代入AB=BA=O可得B11，B12，B21都是零矩阵， 从而

由此即得结论.

出发点2希望考察学生对矩阵的正定性 (半正定性) 与特征值之间关系的掌握和运用. 众所周知， 实对称阵A是正定 (半正定) 矩阵的充分必要条件是A的特征值全为正实数 (非负实数). 进一步， 还有如下结论.

例3设A，B为n阶实对称阵， 求证:

(i) 若A，B均为正定矩阵， 则AB的特征值全为正实数;

(ii) 若A，B均为半正定矩阵， 则AB的特征值全为非负实数; 且AB的特征值全为零的充分必要条件是AB=O.

证只证明 (ii). 由于A为半正定矩阵， 故存在n阶实方阵C， 使得A=C′C. 由教材 [1] 的习题6.1.8知AB=C′CB与CBC′有相同的特征值. 由B的半正定性可得CBC′也是半正定矩阵， 从而其特征值全为非负实数， 即AB的特征值全为非负实数. 若AB的特征值全为零， 则CBC′的特征值全为零， 从而CBC′=O. 由于B为半正定矩阵， 故存在n阶实方阵D， 使得B=DD′， 从而有等式

O=CBC′=C(DD′)C′=(CD)(CD)′，

两边同时取迹可得CD=O. 因此

AB=(C′C)(DD′)=C′(CD)D′=O.

出发点3希望考察学生对由矩阵乘法交换性诱导出来的相关性质的掌握和运用. 当n阶复方阵A，B乘法可交换时， 有许多良好的性质. 例如， (A+B)m可用二项式定理进行展开; A，B有公共的特征向量; A，B可以同时上三角化; 若A，B都可对角化， 则A，B可以同时对角化. 进一步， 我们还有如下结论.

例4设A，B为n阶实对称阵 (实正规阵)， 若AB=BA， 则存在n阶正交矩阵P， 使得P′AP和P′BP都是对角阵 (实正规阵的正交相似标准形).

证参考教材 [1] 的习题9.5.10和习题9.7.3.

相比之下， 矩阵乘法的反交换性给与的性质却较少. 例如， 由AB=-BA一般推不出A，B有公共的特征向量.

命题思路设A，B均为n阶半正定实对称阵， 则由例3(ii) 知AB的特征值全为非负实数， BA的特征值也全为非负实数. 若进一步假设A，B反交换， 即AB=-BA或AB+BA=O， 则AB的特征值全为零. 再次由例3(ii) 知AB=BA=O， 又由例4知A，B可同时正交对角化， 这就是要达到的结论. 经过进一步的分析发现， 可以把A，B的半正定性弱化为其中一个是半正定矩阵即可达到相同的结论. 经过上述的命题思考， 可得到如下题目， 它是复旦大学数学科学学院2013-2014学年第二学期高等代数Ⅱ期末考试的第七大题.

例5设A，B是n阶实对称阵且AB+BA=O. 证明: 若A是半正定矩阵， 则存在正交矩阵P， 使得

P′AP=diag{λ1，…，λr，0，…，0}，P′BP=diag{0，…，0，μr+1，…，μn}.

(2)

命题分析后经统计发现， 复旦大学数学科学学院13级本科生中有30%左右的学生能完整正确地给出本题的证明. 值得一提的是， 学生们共给出了四种不同的证法， 这些证法不仅契合了我们命题时的出发点， 而且还有一种证法完全出乎我们的意料之外. 现将这些证法分述如下. 证法一运用了出发点1中提到的化简技巧.

证法1(利用实对称阵的正交相似标准形理论)由于A是半正定实对称阵， 故存在正交矩阵P， 使得

P′AP=diag{λ1，…，λr，0，…，0}，

其中λi>0(1≤i≤r)，r=rank(A). 在等式AB+BA=O的两边同时左乘P′， 右乘P可得

(P′AP)(P′BP)+(P′BP)(P′AP)=O.

因为结论也在正交相似下保持不变， 所以不妨一开始就假设A是正交相似标准形

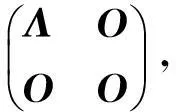
其中Λ=diag{λ1，…，λr}. 设

为相应的分块， 代入AB+BA=O中可得

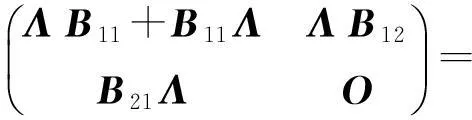
设B11=(bij)1≤i，j≤r， 则

由λi>0 (1≤i≤r)可得bij=0 (1≤i，j≤r)， 即B11=O. 再由Λ的非异性易得B12，B21都是零矩阵， 从而B=diag{O，B22}. 由于B22为实对称阵， 故存在n-r阶正交矩阵Q， 使得

Q′B22Q=diag{μr+1，…，μn}.

令P=diag{Ir，Q}， 则P为n阶正交矩阵使得 (2) 式成立.

虽然反交换的矩阵不一定有公共的特征向量， 但A的半正定性使得我们只需把问题限制在零特征值的特征子空间上讨论即可 (这正是出发点2所强调的)， 此时A，B的反交换性就变成了交换性， 这就是证法二的主要思路.

证法2 (利用不变子空间理论)将问题转化成几何的语言: 设V为欧氏空间，φ为半正定自伴随算子，ψ为自伴随算子且φψ+ψφ=0， 证明存在V的一组标准正交基， 使得φ，ψ在这组基下的表示矩阵为 (2) 式中的对角阵.

设φ的全体不同特征值为λ1，…，λk， 对应的特征子空间为V1，…，Vk， 则λi≥0且

V=V1⊥…⊥Vk.

任取非零向量α∈Vi， 则φ(α)=λiα. 在φψ+ψφ=0两边同时作用α可得

φ(ψ(α))=-λiψ(α).

如果能直接证明AB=O， 则AB=BA=O， 由例4即可得到要证的 (2) 式 (这正是出发点3 所强调的). 接着给出证法3.

证法3(利用实反对称阵的正交相似标准形理论)注意到

(AB)′=B′A′=BA=-AB，

即AB是实反对称阵.可断言AB=O. 用反证法， 若AB为非零实反对称阵， 则存在n阶正交矩阵P， 使得

其中bi≠0 (1≤i≤r)，r≥1. 设P的前两个列向量为α1，α2， 则有

ABα1=-b1α2，ABα2=b1α1.

由A的半正定性可得

α′1BABα1=-b1α′1Bα2≥0，

α′2BABα2=b1α′2Bα1=b1α′1Bα2≥0，

从而有

α′1BABα1=-b1α′1Bα2=0.

再次由A的半正定性可知， 存在n阶实方阵C， 使得A=C′C. 因此我们有

0=α′1BABα1=α′1BC′CBα1=(CBα1)′(CBα1)，

故CBα1=0， 从而

ABα1=C′CBα1=0，

于是b1α2=0， 这与b1≠0， α2≠0矛盾. 因此AB=BA=O， 由例4知A，B可同时正交对角化， 从而结论即得.

虽然上述方法证明了A，B可同时正交对角化， 但证明AB=O的过程过于技巧化， 能想到实属不易. 然而， 复旦大学数学科学学院13级一位同学却另辟蹊径， 利用A2，B可同时正交对角化来进行证明， 这种方法来的更自然， 也很巧妙， 让我们任课老师赞叹不已.

证法4(利用半正定矩阵的算术平方根)由AB=-BA，可得

A2B=-ABA=BA2，

即A2与B可交换. 由例4知存在n阶正交矩阵P， 使得

(3)

其中λi>0 (1≤i≤r)， r=rank(A). 注意到

P′A2P=(P′AP)2=diag{λ1，…，λr，0，…，0}2，

由于A是半正定矩阵， 故P′AP与diag{λ1，…，λr，0，…，0}都是P′A2P的算术平方根. 由半正定矩阵算术平方根的唯一性 (参考教材 [1] 的推论9.8.2) 可得

P′AP=diag{λ1，…，λr，0，…，0}.

(4)

将 (3) 式和 (4) 式代入AB+BA=O中可得μ1=…=μr=0， 结论得证.

高等代数是数学系本科生的基础课程之一， 所授内容均相对成熟和固定. 如何通过期末考试等形式更好的考察学生对所授知识的理解和掌握， 切实起到引领学生进行有效学习的指挥棒的作用， 这是一个值得研究的课题. 复旦大学数学科学学院代数组在高等代数的命题方面进行了多年的探索 (参考论文 [2])， 本文所阐述考题的命题思路及分析正是在这一探索过程中得到的一些经验和体会， 希望同行专家多多指正.

致谢在本文的撰写过程中， 得到了复旦大学数学科学学院姚慕生教授、吴泉水教授、朱胜林教授的热心指导和大力斧正， 在此谨表示衷心的感谢.

[参考文献]

[1]姚慕生， 吴泉水， 谢启鸿. 高等代数学[M].3版.上海: 复旦大学出版社， 2014.

[2]谢启鸿. 浅谈高等代数命题中的若干技巧[J]. 大学数学， 2013， 29(3): 127-130.

The Analysis of Setting an Examination Question in Advanced Algebra

XIEQi-hong

(School of Mathematical Sciences， Fudan University， Shanghai 200433， China)

Abstract:We illustrate the analysis of setting the last question of the final examination of Advanced Algebra II in the second semester of the 2013-2014 school year in Fudan University.

Key words:real symmetric matrix; positive semi-definite matrix; eigenvalue; anti-commutativity

[基金项目]复旦大学数学科学学院数学类基础课程教学团队(国家级)项目

[收稿日期]2014-04-28

[中图分类号]O151.21

[文献标识码]C

[文章编号]1672-1454(2015)01-0070-05