一种方阵的反问题解
杨恩孝,许佰雁
(长春光华学院基础部,吉林长春130033)
给定一个方阵,可求其特征值和特征向量,且特征值和特征向量具有一些很好的性质。但反过来,若已知某方阵的特征值和对应的特征向量,如何求出原矩阵呢?这类问题,我们称之为矩阵反问题[1-3]。主要根据特征值的某些特点,给出一种反求矩阵的具体方法,并举例验证。
1 n阶方阵有n个不同的特征值
定理1若n阶方阵A有n个互不相同的特征值λ1,λ2,…,λn,与其对应的特征向量分别为α1,α2,…,αn,则存在可逆矩阵P,使得方阵
A=PΛP-1,
证明由矩阵特征值的性质知,属于不同特征值的特征向量必无关,故 α1,α2,…,αn无关。令P=(α1,α2,…,αn),则 P 可逆。又因为 Aαi=λiαi(i=1,2,…,n),故

即AP=PΛ,其中

例1已知某三阶方阵A的特征值分别为λ1=1,λ2=-1,λ3=2 ,对应的特征向量为 α1=(1,0,-1)T,α2=(0,0,1)T,α3=(2,1,-2)T,求矩阵A。
解由于特征值互不相同,故矩阵P可逆,则

由上述定理知:
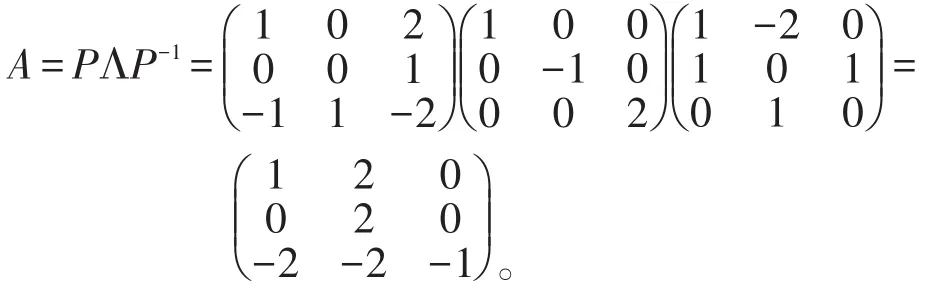
2 n阶方阵有多个重特征值
定理2若n阶方阵A有m个互不相同的特征值 λ1,λ2,…,λm,其中 λ1为 k1重、λ2为 k2重、…、λm为km重,k1+k2+…+km=n。不同的特征值具有与重数相同的个数的特征向量,分别为α1,α2,…,αk1,β1,β2,…,βk2,…,γ1,γ2,…,γkm则
A=PΛP-1,
其中P=(α1,α2,…,αk1,β1,β2,…,βk2,…,γ1,γ2,…,γkm),
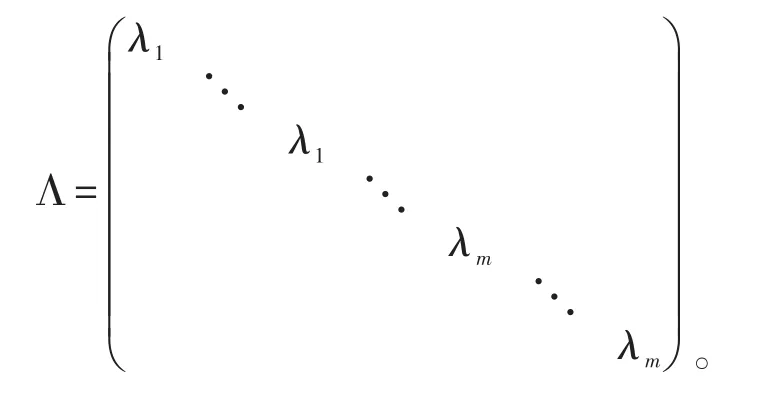
证明同定理1。
例2已知某三阶方阵A的特征值分别为λ1=λ2=1,λ3=-2 ,对应的特征向量分别为α1=(-2,0,1)T,α2=(0,0,1)T,α3=(-1,1,1)T,求矩阵 A。
解令
由于特征值互不相同,故矩阵P可逆,则

由上述定理知,
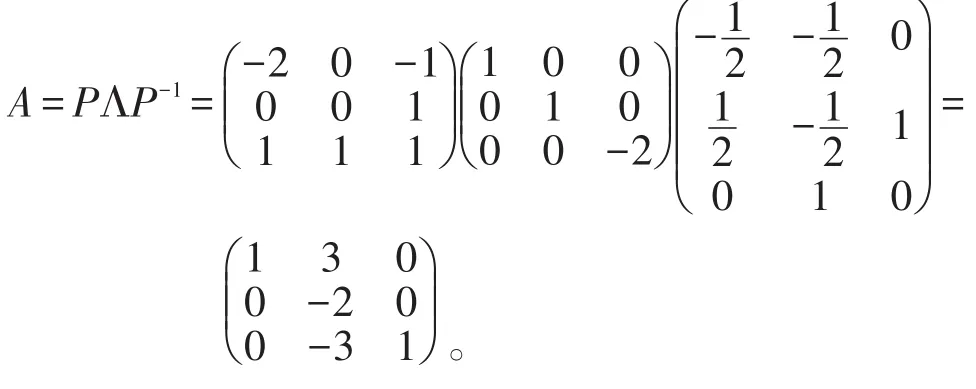
3 n阶实对称方阵有多个重特征值
说明:n阶实对称方阵有n个互不相同特征值时的结论同定理1。
引理1设n阶实对称矩阵 A的特征值为λ1,λ2,其重数分别为1,n-1,与 λ1特征值对应的特征向量为α1,则

引理2设n阶实对称矩阵 A的特征值为λ1,λ2,其重数分别为k,n-k,与λ1特征值对应的k个两两正交的单位特征向量为α1,α2,…,αk,则

上述引理(见文献3)只给出了n阶实对称方阵有2个互不相同特征值时的结论,下面我们给出3个不同特征值的结论。
定理3设n阶实对称矩阵 A的特征值为λ1,λ2,λ3,其重数分别为 k1,k2,k3,与 λ1特征值对应的k1个两两正交的单位特征向量为α1,α2,…,αk1,与λ2特征值对应的k2个两两正交的单位特征向量为β1,β2,…,βk2,则

证明不妨设与λ3特征值对应的k3个两两正交的单位特征向量为 γ1,γ2,…,γk3,有实对称矩阵特征向量的性质,现在所有的特征向量都是单位正交向量。令
P=(α1,α2,…,αk1,β1,β2,…,βk2,γ1,γ2,…,γk3),则

所以


例3已知5阶实对称矩阵A的特征值为1,1,2,2,10,对应于特征值λ1=1的特征向量为X1=(- 2,1,0,0,0)T,X2=(2 ,0,1,0,0)T,对应于特征值λ2=2的特征向量为X3=(0 ,0,0,1,0)T,X4=(0 ,0,0,0,1)T,求实对称矩阵A。
解由于属于特征值λ1=1的两个特征向量无关,但不正交。故由施密特正交化方法,令X1′=X1=(- 2,1,0,0,0)T,则

令
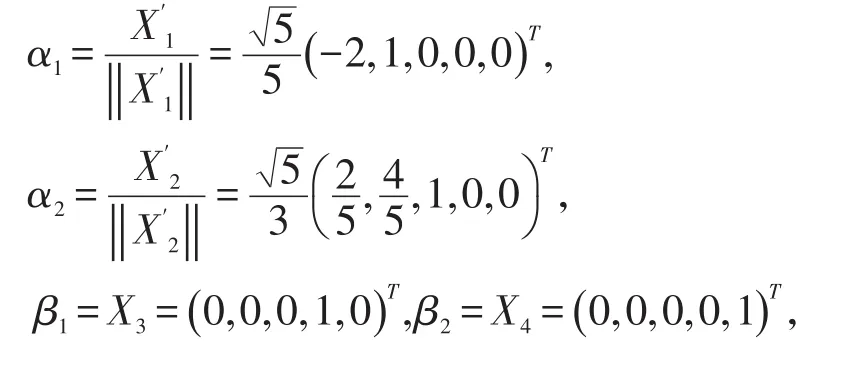
由定理3,可知

定理3还可以推广到特征值为3个以上,利用此方法可以解决矩阵的反问题。

