离散数学教学改革浅谈

王也洲，　杨　春，　黄廷祝，　李艳馥

(1. 电子科技大学数学科学学院，四川成都611731； 2. 高等教育出版社理工事业部，北京100120)



离散数学教学改革浅谈

王也洲1，杨春1，黄廷祝1，李艳馥2

(1. 电子科技大学数学科学学院，四川成都611731； 2. 高等教育出版社理工事业部，北京100120)

[摘要]针对如何提高《离散数学》教学水平问题，提出了“赋予逻辑符号生动语言，激发学生学习兴趣”、“多角度讲解关系运算，启发学生发散思维”、“数学文化融入课堂教学，拓宽学生知识层面”的教学改革措施.

[关键词]离散数学； 教学改革； 数学文化

1引言

《离散数学》是高等院校计算机及通信专业的一门专业核心课程，主要研究有限个或无限个离散变量之间的关系及结构特征.该课程基础性强，对学生知识与能力的培养至关重要.此外，该课程具有概念多、结构散、内容抽象、理论性强的特点，给教师的日常教学和学生的平时学习带来一定的困难.因此，如何改进教学方法、提高教学水平逐渐成为一个非常有价值的研究问题.国内一些学者经过大胆尝试、努力钻研，已在这方面取得了一些不错的成绩，譬如，肖利芳、段梅[1]提出“以学生为主导，以教师为辅，结合实际问题考核”的教学模式；刘海英[2]得出“以教师、学生、媒体、教学内容为教学四要素，建设离散数学网络课程”的教学方法.

近几年来为加强创新人才培养，我们在《离散数学》课程的教学实践中也做了大量的探索与改革，获得了一定的方法，总结了一定的经验，也取得了一定的成效.下面就该课程教学改革中所实施的一些具体方法谈一些体会.

2赋予逻辑符号生动语言，激发学生学习兴趣

数理逻辑是一门研究演绎推理的学科，是数学基础理论不可缺少的一个组成部分.它采用数学符号化的方法， 给出推理规则来建立推理体系，进而讨论推理体系的一致性、可靠性和完备性等.

数理逻辑部分，公式繁多，不宜记忆，学生难以接受，但它是培养学生逻辑推理能力的重要内容.因此在离散数学教学中，数理逻辑部分是教学的重点之一.针对数理逻辑部分的教学，蹇柯[3]提出了“设置悬疑、深入生活、注重类比”的教学理念，加深了学生对数理逻辑的理解，教学效果得到明显提高.

经过多年的教学，我们发现林林总总的符号、形式多样化的公式并非枯燥无味，难以琢磨，相反可以用形象的语言来表达.下面，我们从若干方面来加以说明.

2.1　“说了算”与“算说了”

在析取式中，只要有一个公式为真，则整体为真，而永假式的出现并不影响析取式的真值.因此，公式“G∨1=1”可以描述为：永真式在析取式中“说了算”；公式“G∨0=G”可以描述为：永假式在析取式中“算说了”.

只有各个公式的真值均为真时，合取式的真值才为真；只要有一个公式真值为假，则整个合取式真值为假.因此，公式“G∧1=G”可以描述为：永真式在合取式中“算说了”；公式“G∧0=0”可以描述为：永假式在合取式中“说了算”.

“说了算”，表示起决定性作用；“算说了”，表示不影响最终结果.“说了算”与“算说了”这样一种教学技巧，不仅可以帮助学生记忆这四个基本等价公式，而且有助于学生理解公式的判定和主范式的求解.

在公式的判定问题中，我们实际只需要关心“说了算”的子公式，而“算说了”的子公式完全可以置之不理.

在主析取范式与主合取范式的求解过程中，我们需要去掉析取范式中所有永假公式的短语和合取范式中所有永真公式的子句，实则我们需要去掉的是“算说了”的子公式.

2.2　基本蕴含关系的自然语言解释

在命题逻辑的推理理论中，15个基本蕴含关系发挥着极其重要的作用.在通常的教材中，只是简单地罗列出这些基本蕴含关系，并没有给出详细的证明.虽然，利用真值表技术不难给出每个蕴含关系的详细证明，但不适合于在课堂上开展这项工作.如何利用较短的时间向学生们解释清楚这些蕴含关系的内涵，同时希望学生能够正确理解和熟练掌握是值得教学工作者思考的一个问题.

既然逻辑学是研究人的思维形式和规律的科学，那么现有的这些符号体系一定可以用人类的自然语言来解释.通过仔细研究，我们合理地给出了15个基本蕴含关系的语言解释，由于篇幅限制，我们这里只列举一些不太容易理解的蕴含关系.

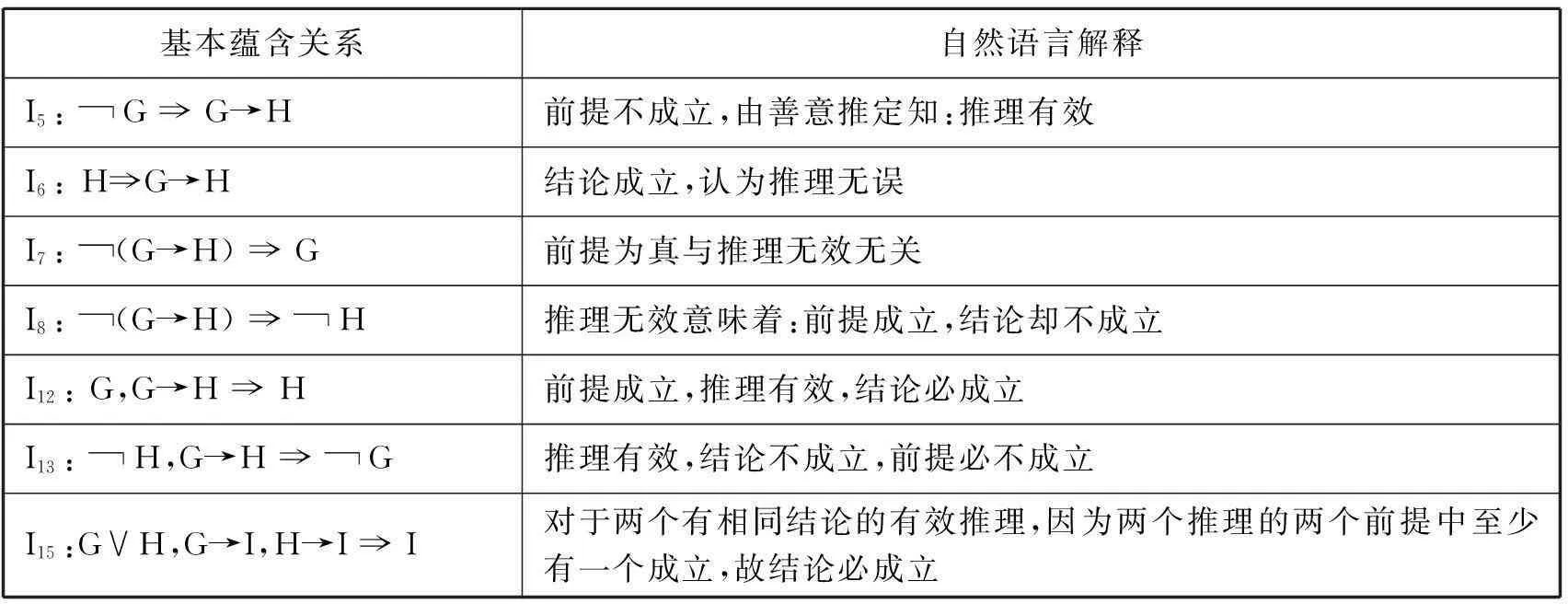
表1　基本蕴含关系与语言解释

谓词逻辑与命题逻辑相比，由于谓词逻辑引入了全称量词与存在量词，使得谓词逻辑的推理规律要比命题逻辑的推理规律复杂的多.但即便如此，只要善于思考，也不难找到谓词逻辑推理规律的自然解释.下面以两条推理规律为例，做一个简单介绍.

假设G(x)，H(x)是只含自由变元x的公式，则在全总个体域中，

(∀x)G(x)∨(∀x)H(x)⟹(∀x)(G(x)∨H(x))

可以解释为：要么G(x)对所有x成立，要么H(x)对所有x成立，那么对每一个x，G(x)与H(x)至少有一个成立.

类似地，(∀x)(G(x)→H(x))⟹(∀x)G(x)→(∀x)H(x)可以形象地解释为：在每个x处，只要G(x)成立，便可得到H(x)也成立，因此当G(x)对所有x成立时，自然可以推出H(x)对所有x也成立.

在教学实践中，我们发现对抽象的数学符号及公式赋予生动的语言，可以使得学生对理论问题产生浓厚的学习兴趣，进一步可以激发学生主动探索数学理论与客观世界之间的内在联系.

3多角度讲解关系运算，启发学生发散思维

关系理论最早出现在德国数学家Felix Hausdorff于1914年编写的著作《集论基础》的序型理论中，它与集合论、数理逻辑以及组合数学、图论、布尔代数等都有密切联系.

关系运算是关系理论的一个重要组成部分，如何让学生正确理解和熟练掌握各种关系运算是离散数学教学改革的一个重点.在这方面，总结出“从定义严格证明”、“从关系矩阵简洁证明”、“从关系图直观理解”的教学方法.下面，以“关系的复合运算满足结合律”为例来加以说明.

例设A，B，C和D是任意四个非空集合，R⊆A×B，S⊆B×C，T⊆C×D，则

(R∘S)∘T=R∘(S∘T).

从定义严格证明关系是以序偶为元素的特殊集合，关系进行运算之后的结果仍然是集合，所以该结论实际上是要证明两个集合相等，从而只需证明等式两端的集合相互包含即可.

对∀〈a，d〉∈(R∘S)∘T，由“∘”的定义知，存在c∈C，使得〈a，c〉∈R∘S且〈c，d〉∈T.

又因为〈a，c〉∈R∘S，所以存在b∈B，使得〈a，b〉∈R且〈b，c〉∈S.因为〈b，c〉∈S且〈c，d〉∈T，由“∘”的定义知，〈b，d〉∈S∘T；又由〈a，b〉∈R，进而〈a，d〉∈R∘(S∘T).所以(R∘S)∘T⊆R∘(S∘T).

同理可证：R∘(S∘T)⊆(R∘S)∘T.

从关系矩阵简洁证明如果两个关系所对应的关系矩阵完全相等，则说明这两个关系也完全相等.因此，我们只需证明左右两端对应的关系矩阵相等即可.

利用布尔积满足结合律这条性质，很容易得到

M(R∘S)∘T=MR∘S⊙MT=(MR⊙MS)⊙M

=MR⊙(MS⊙MT)=MR⊙MS∘T=MR∘(S∘T).

从关系图直观理解两个关系进行复合运算体现在关系图上就好比是在对应的集合之间寻找通路.R∘S等效于借助集合B中的元素寻找A与C之间的通路，S∘T等效于通过集合C中的元素寻找B与D之间的通路.最终目标是通过中间集合B与C中的元素寻找集合A与D之间的通路，可以由以下两种方式来实现：

(i) 从A出发，借助B中元素间接达到C中某个元素；然后通过C与D之间的边直接到达D中某个元素，用数学语言来描述即为：(R∘S)∘T;

(ii) 从A出发，通过A与B之间的边直接到达B中某个元素；然后借助C中元素间接到达D中某个元素，用数学语言来描述即为：R∘(S∘T).

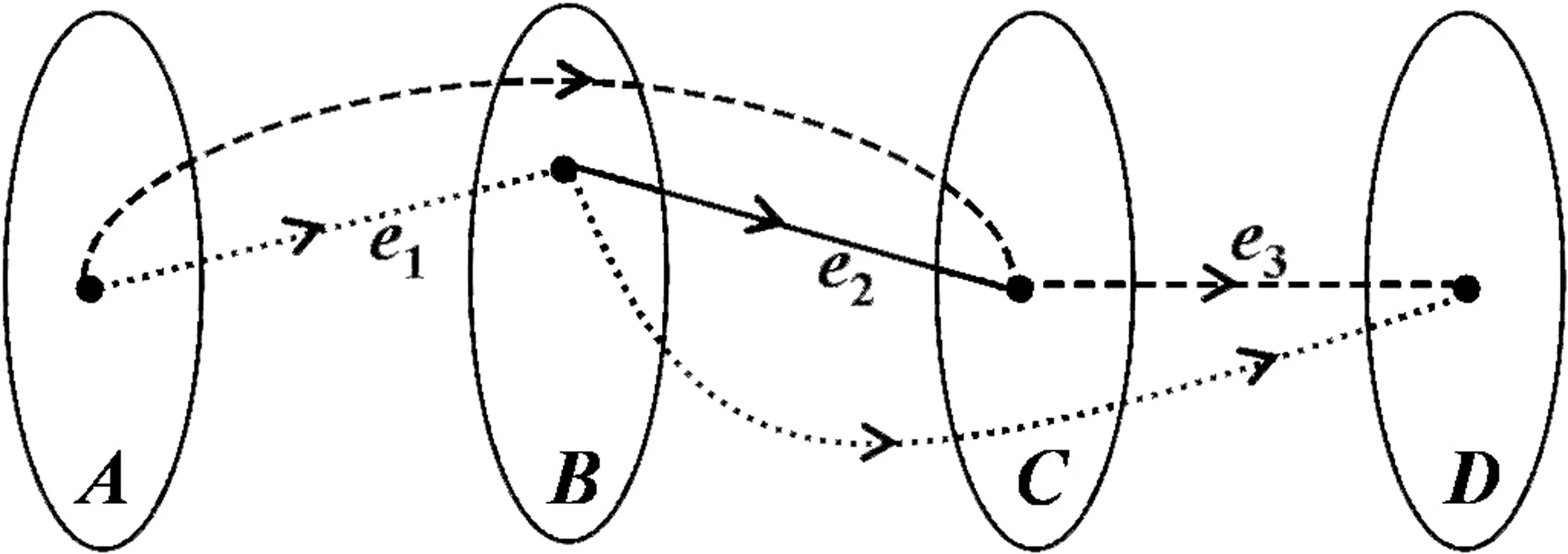
图1　寻找通路的两种方式

在图1中，用两种不同的虚线表示两种寻找通路的方式.从图中可以看出，两种方式经过的边完全相同，均为e1，e2和e3.两条通路只是表现形式不同，第一条通路把边e1和e2当成一个整体，第二条通路把边e2和e3看成一个整体，二者实则完全等同.

比较以上三种证明方法，不难看出：“按照定义证明”方法初等，过程严谨，但颇为繁琐，学生容易在证明过程中迷失方向；“按照关系矩阵证明”过程简洁，但要求学生首先掌握布尔积运算的一些性质；“按照关系图证明”形象直观，但缺乏严谨性.

三种方法各有利弊，若将三种方法结合起来讲解，譬如，先按照定义证明，使得学生有一个大致认识；再按照关系矩阵证明，可以进一步加深学生对问题的理解；最后从关系图证明，使得学生对问题的理解一目了然.这样一种循序渐进的讲解过程不仅有助于加深学生对问题的理解，而且有助于培养学生的发散思维.

以上方法也适用于关系的其他运算，如逆运算、幂运算、复合运算与逆运算的复合等，同时也适用于关系性质的讲解，由于篇幅限制，在此就不一一详细说明.

4数学文化融入课堂教学，拓宽学生知识层面

正如当代美国数学家、史学家、教育家Morris Kline[5]所说，“数学不仅是一种方法、一门艺术、一种语言，数学还是一门有着丰富内容的知识体系，其内容对自然科学家、社会科学家、哲学家、逻辑学家和艺术家十分有用，同时影响着政治家和神学家的学说；满足了人类探索宇宙的好奇心和对美妙音乐的冥想；有时甚至可能以难以察觉到的方式但无可置疑地影响着现代历史的进程.”

数学文化具有培养科学精神的价值，具有完善自我的人生价值，具有健全自我人格的价值，具有提升人类审美水平的价值.从这个意义上说，将数学文化融入到离散数学教学中，让更多的大学生，特别是非数学专业的本科生多了解点数学文化知识是很有必要的，也是非常重要的.

4.1　从哥尼斯堡七桥问题到中国邮递员问题

图论是离散数学的一个重要组成部分，为了激发学生学习图论的兴趣，在讲解到图论部分时，不可或缺地要介绍著名的哥尼斯堡七桥问题.这一事件不仅标志着图论学科的诞生，而且促进了拓扑学的萌芽.伟大数学家欧拉是这一事件的一位至关重要的当事人，他不仅成功地给出了该问题的一个否定回答，而且引领人类踏上欧拉图研究的征程.

基于欧拉图这一模型，1960年时任山东师范大学讲师的管梅谷先生提出了著名的中国邮递员问题.这一问题为我国在近代世界数学史上赢得了一席之地(在世界数学史上，冠以中国两字的数学概念及定理屈指可数，据我们所知，除了中国邮递员问题外，中国剩余定理代表了古代数学理论的一个高度).

以哥尼斯堡七桥问题为起点，游历中国邮递员问题，追溯中国剩余定理，从西方到东方，从近代到古代，这样一种教学方式不仅可以激发学生学习图论的兴趣，而且可以更好地让学生了解中国数学的发展，乃至世界数学的演绎.

4.2　谷歌Logo中的数学文化

枯燥的数学概念，难免会让学生感到烦躁，在讲解知识的同时，介绍数学家的生平，不失为引发学习兴趣的一种方法.在离散数学课程中，随处可见数学大师欧拉的杰作，比如握手定理、平面图的欧拉公式等.在讲解到这些结论时，重点介绍欧拉是一位多产的数学家，一生发表论文850余篇，在20世纪之前，欧拉是发表论文最多的数学家，紧随其后的是数学家柯西(发表论文789篇).这一记录被20世纪匈牙利数学家Erdos打破，其一生发表论文1525篇，他不仅是20世纪最伟大的数学家，也是人类历史上发表数学论文最多的数学家.

为了纪念欧拉这一伟大的数学家，著名互联网谷歌通常在欧拉诞辰之日，即4月15日这一天，会在其Logo中融入欧拉的许多数学成就，如图2所示.

图2　谷歌Logo中的数学文化

离散数学中，有很多知识点可以引出数学文化的讲解，比如集合论公理化体系建立过程中的“罗素悖论”、组合数学中的“斐波那契兔子问题”，数理逻辑中的“逻辑学家与生死门”的趣味故事等.

将数学文化融入课堂教学，有助于拓宽学生的知识层面，培养学生的人文精神.通过融入数学文化的内容，可以让学生更好地了解和体会数学的内涵，体会数学在人类文明进程中的影响和作用，可以带给学生一种新观念、新思维、新思想.

5结语

随着计算机科学与技术的发展，离散数学作为一门专业基础核心课程，其教学方式需要不断地研究、总结和创新.只有在教学过程中不断探索、深入实践、改进方法，才能更好地提高离散数学的教学质量.

[参考文献]

[1]肖利芳， 段梅. 离散数学教学模式的改进与创新[J]. 中国电力教育， 2014(11): 129—131.

[2]刘海英. 离散数学课程教学改革初探[J]. 赤峰学院学报， 2014， 30(6)：3—4.

[3]蹇柯. 离散数学中数理逻辑部分的教学方法刍议[J]. 课程教育研究， 2014(3): 254—255.

[4]傅彦， 顾小丰， 王庆先， 刘启和. 离散数学及其应用[M]. 北京: 高等教育出版社， 2013.

[5]克莱因.西方文化中的数学[M].上海: 复旦大学出版社， 2005.

Introduction to Teaching Reform on Discrete Mathematics

WANGYe-zhou1，YANGChun1，HUANGTing-zhu1，LIYan-fu2

(1.School of Mathematical Sciences，University of Electronic Science and Technology of China，Chengdu 611731，China;

2. Division of Science and Engineering， Higher Education Press， Beijing 100120， China)

Abstract:For the problem of raising the teaching level of Discrete Mathematics， we propose several concrete reform methods. They are respectively endowing the logic symbols with vivid description to attract students’ interests; explaining relation operations in many ways to enlighten students’ thoughts; infusing mathematical culture into teaching to broaden students’ knowledge.

Key words:discrete mathematics; teaching reform; mathematical culture

[基金项目]电子科技大学教育教学改革研究项目(2013XJYEL032)

[收稿日期]2014-10-10

[中图分类号]G642.0

[文献标识码]C

[文章编号]1672-1454(2015)01-0048-05