突破数学教学困境的策略性研究

温庆庆

【摘 要】现代教育所提倡的学生的主体性与全面发展被人们抛诸脑后，学生求知欲不强甚至产生厌学情绪，中学数学教学陷入一个尴尬困境，如何突破中学教学困境，解决这些教学难题成为一个至关重要的课题。本文就这一课题进行发现性的研究，并尝试对此提出具体的解决方案。

【关键词】教学改革 教学困境 求知欲 解题方法 数学思维

数学是一门锻炼人的思维模式与能力的学科，邱成桐说：“现代高能物理到了量子物理以后，很多内容根本无法做实验，在家用纸笔来算，这跟数学家想象的差不了多远，所以说数学在物理应用上有着不可思议的力量。”这话阐释了数学对于物理的重要作用。相比而言，伦琴在说明数学的重要性时则显得更加简单明了，他说：“第一是数学，第二是数学，第三是数学。”一句简单得不能再简单的话便将数学无可比拟的重要地位表露无遗。闻名世界的数学家华罗庚也说：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。”而一代枭雄拿破仑也说：“一个国家只有数学蓬勃发展，才能展现它国力的强大。数学的发展和至善与国家繁荣昌盛密切相关。”数学如此之重要，我们又怎能忽视它的教学与发展呢？

一、让学生爱上数学，增强学生的求知欲

中学数学教学不同于初级数学教学，它达到了一个新的阶段和高度，对于学生来说是新的课题与挑战，它需要学生付出时间与精力，并要求学生多动脑多思考，如若不然，学生的成绩很有可能会下滑、不尽如人意，继而容易产生厌学情绪，甚至产生放弃的念头。针对这种现象，教师应该多给予学生引导与帮助，让学生感觉自己不是孤独无助的，并且情况也不是那么的糟。

激发学生的求知欲，让学生爱上数学，可以让学生发现数学的“美”，让他们认识到其实数学并非什么洪水猛兽，相反它是神奇美妙的。想当年笔者也是数学的门外汉，而且对数学一直没感觉，但是换了一个数学老师后，这位数学老师总是能给我们呈现数学的奇妙，每道题他总能异于常人，给我们更精巧的方法。正所谓条条道路通罗马，而他所讲的方法总像当头棒喝，让你感叹，原来如此简单。长此以往，我们也在解题中感受到了每想到一种解题方法都犹如发现新大陆般的喜悦，并在此过程中逐渐爱上数学。

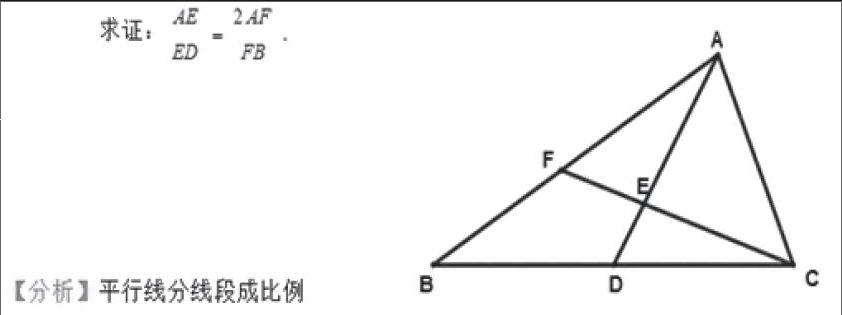
例如下面这道题中，解题方法就有很多种。解题思路有连接BE、过D作DM与CF平行并与AB相交于M、过D作DN与AB平行并与CF相较于N、过B作BG与CF平行并与AD的延长线相交于G、过B作BH与AD平行并与CF延长线相交于H、过A作AK与BC平行并与CF延长线相交于K、过A作AP与CF平行并与BC延长线相交于P，或者是过D作DP与AC平行并与CF延长线相交于P并交AB于Q。就这么一道题，解题思路便有八种之多，相信学生在学习之后定会惊叹数学的奇妙。其实这种数学题又岂止少数呢？

二、数学不只是解题，更要培养学生的数学思维

如果把数学比喻成一棵树，那么数学思维就是这棵树的根，毋庸置疑，只有根深才能叶茂。如果只是把数学当成是一门解题的学科，那么，题海无量，无论是老师抑或是学生，都将沉溺于无量题海之中难以自拔，其结局也不言而喻。数学是一门有思想有体系的学科，真正要教好学生，教师们要做的是培养学生的数学思维。授人以鱼不如授人以渔，学生终究是学生，他们需要老师的引导。相信当老师将一道题的解题方法告诉学生们时，只会有极少同学主动发现这一方法的解题思路，并吸收为己用。既然如此，教师就应该主动承担引导学生动脑思考的责任。

在上一道题中，八种解题方法都有着同一个目的，那就是证明题中论题。从这一目的出发，解题方法也自然而然想出，但是在这一过程中，起着最为关键作用的是数学思维，是数学思维主导并引导学生去发现这些连接线并解决这一道题。

再例如，一元二次方程的解题方法有公式法、直接开平方法、配方法和因式分解法，教会学生用不同的方法去解题，培养学生的数学思维可以使学生在遇到问题时学会从不同角度去思考与解决问题，而不是一条路走到黑也走不出来。这也能提高学生对数学学习的自信心，不至于对数学学习失去耐心。老师们要做学生的点灯人，点醒迷茫中的学生；老师们要做学生的指航灯，为学生的前行指明方向；老师们要做学生的引路人，引导学生形成正确的思维发展道路。

数学是树，树的枝叶不用太多，太多了学生会累而且效果也并不一定就好。再多的叶也是源于根，所以再多的叶的解题方法都在根上。同样的，再多的题都终将回归到数学思维上。做题不在于多，而在于精，明白解题思路，形成自己的数学思维，否则做再多的题也是无益的。