一种工业机器人动力学参数的辨识方法

一种工业机器人动力学参数的辨识方法*

丁亚东陈柏†吴洪涛申浩宇

(南京航空航天大学 江苏省精密与微细制造技术重点实验室， 江苏 南京 210016)

摘要：机器人动力学参数辨识方程随着关节的增多变得更加繁琐，关节数超过4个后，甚至难以获得准确的参数辨识方程.为此，文中提出一种分步辨识的方法.该方法每次辨识的惯性参数较少，辨识方程相对简单，计算量小，辨识累计误差小，能很好地实现对超过四自由度的关节机器人动力学参数的辨识.文中还以某型六自由度关节机器人为对象，设计了辨识实验，对分步辨识方法进行了验证.结果表明：在保有机器人关键动力学特性的情况下，文中方法能简单而有效地获得机器人的关键动力学参数.

关键词：工业机器人；动力学参数；分步辨识；辨识算法；轨迹优化

中图分类号：TP242

doi：10.3969/j.issn.1000-565X.2015.03.008

文章编号：1000-565X(2015)03-0057-09

收稿日期：2014-08-21

基金项目：* 国家自然科学基金资助项目(61471173)

作者简介：马丽红(1965-),女,博士,教授,主要从事图像视频信号处理、容错编码和数据隐藏、模式识别研究. E-mail: eelhma@scut.edu.cn

随着工业机器人向高速、高精度的方向发展，用户对工业机器人的控制精度提出了更高的要求.目前，大多数国产机器人仍使用简单的比例-积分-微分(PID)运动控制，并未考虑机器人的动力学特性，这就限制了机器人的精度和性能.之所以大多数控制器未考虑机器人的动力学特性，其中一个重要的原因是难以获得精准的动力学参数，而不精确的动力学参数不仅无法带来机器人性能的提高，甚至可能导致系统失稳.因此，获取精确的机器人动力学参数变得尤为重要[1-2].机器人结构的复杂性使得人们无法直接测量这些参数，而从CAD软件中得出的惯性参数由于未能对机器人每个零件进行精确建模而难以达到所需的精度.因此，基于实验的机器人参数辨识是唯一有效的获取精确动力学参数的方法[3-4].

机器人动力学参数辨识主要有两类方法：①采用一次性辨识全部惯性参数的方法得到机器人的动力学参数[5-6].该方法随着关节参数的增多，所用到的逆动力学辨识模型的符号表达式就越发复杂，需辨识的参数，关节的角位移、角速度、角加速度累积误差也会相应的增加，进而导致辨识难度加大，辨识精度降低，辨识轨迹的优化难度也相应增加.②简化辨识模型，一些研究者提出分开辨识机器人的惯性参数.Atkeson等[7]提出顺序辨识方法，每次辨识时只驱动部分关节轴.该方法所需的辨识次数繁多，每次辨识时未考虑连杆之间的耦合.Dutkiewicz等[8]只使用单个关节和两个关节同时运动来辨识惯性参数，由于已辨识的参数值在辨识剩余参数时被用作先验值，因而会产生累积误差.Vandanjon等[9]为避免此缺点，提出使用4条轨迹分别辨识出机器人的惯量矩、速度项、惯量积和重力项.Daemi等[10]提出先辨识每个连杆的摩擦模型，然后，在辨识机器人连杆惯性参数前补偿其对测量力矩的影响.然而，机器人操作环境的变化使得准确的摩擦补偿难以达到.

综合上述各类辨识方法，并鉴于机器人肘部1、2、3连杆和腕部4、5、6连杆惯性参数值的巨大差异，将机器人分为1、2、3关节和4、5、6关节两步辨识.4、5、6连杆惯性参数相对于1、2、3连杆惯性参数较小，其对1、2、3关节贡献的电机力矩很小，故而，由此辨识出来的1、2、3连杆的惯性参数和实际值非常接近；4、5、6连杆的惯性参数辨识结果与一次辨识结果一致；辨识的难度大大降低，辨识更具针对性且利于轨迹优化.针对上述分步辨识的方法，文中设计了辨识实验，验证了其可行性和正确性

1机器人动力学模型

用牛顿-欧拉法或拉格朗日法得出n自由度串联机器人的动力学方程：

(1)

(2)

式中，θdyn为10n×1的惯性参数向量，Φdyn为n×10n的观测矩阵.机器人关节力矩的线性特性大大简化了参数辨识过程[4,11-12].

方程(1)和(2)只包含了驱动连杆运动所需的关节力矩，而实际上，关节摩擦、电机转子的转动惯量等同样影响机器人的动态行为，需要消耗一定的电机力矩.其中，电机转子的转动惯量一般出厂给定，无须包括进辨识模型，只需将转子产生的惯性力矩补偿到力矩方程.尽管实际的关节摩擦模型在电机反转时是个复杂的非线性模型，但在机器人辨识应用中，综合考虑辨识效率、精度与成本，通常在参数线性化的摩擦模型中只考虑库伦摩擦和粘滞摩擦[13].关节i的摩擦力矩为

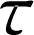
(3)

组合方程(2)和方程(3)得到完整的机器人惯性参数线性方程：

(4)

θsi=(Ixxi,Ixyi,Ixzi,Iyyi,Iyzi,Izzi,mirxi,miryi，mirzi,mi,fci,fvi)T

(5)

式中，Ixxi、Ixyi、Ixzi、Iyyi、Iyzi、Izzi为连杆i相对于坐标系i原点的惯性张量的各项，mirxi、miryi、mirzi为连杆i相对于坐标系i原点的一阶惯量矩(r为质心位置向量)，mi为连杆i的质量.

除摩擦参数外，机器人连杆的惯性参数称为经典惯性参数，但由于方程(4)中辨识矩阵Φs不是满秩矩阵，所以并不是每个惯性参数都对力矩有影响，只有部分惯性参数对机器人动态有影响.为此，在动力学方程中，通过一定的线性关系重组一些惯性参数或使用简单的封闭形式规则消去一些惯性参数来得到一组最小惯性参数十分必要[4,14].只包含最小惯性参数的动力学模型可表示为

(6)

2动力学参数辨识过程

机器人动力学参数辨识一般包含激励轨迹设计、数据采样及处理、参数估计和模型验证4个步骤.机器人动力学参数辨识过程可表述为：给定机器人关节激励轨迹，采集关节力矩和角位移数据，数据经过处理后带入到辨识方程中，便可得到机器人连杆的惯性参数.其流程如图1所示(Y是处理后的力矩向量).

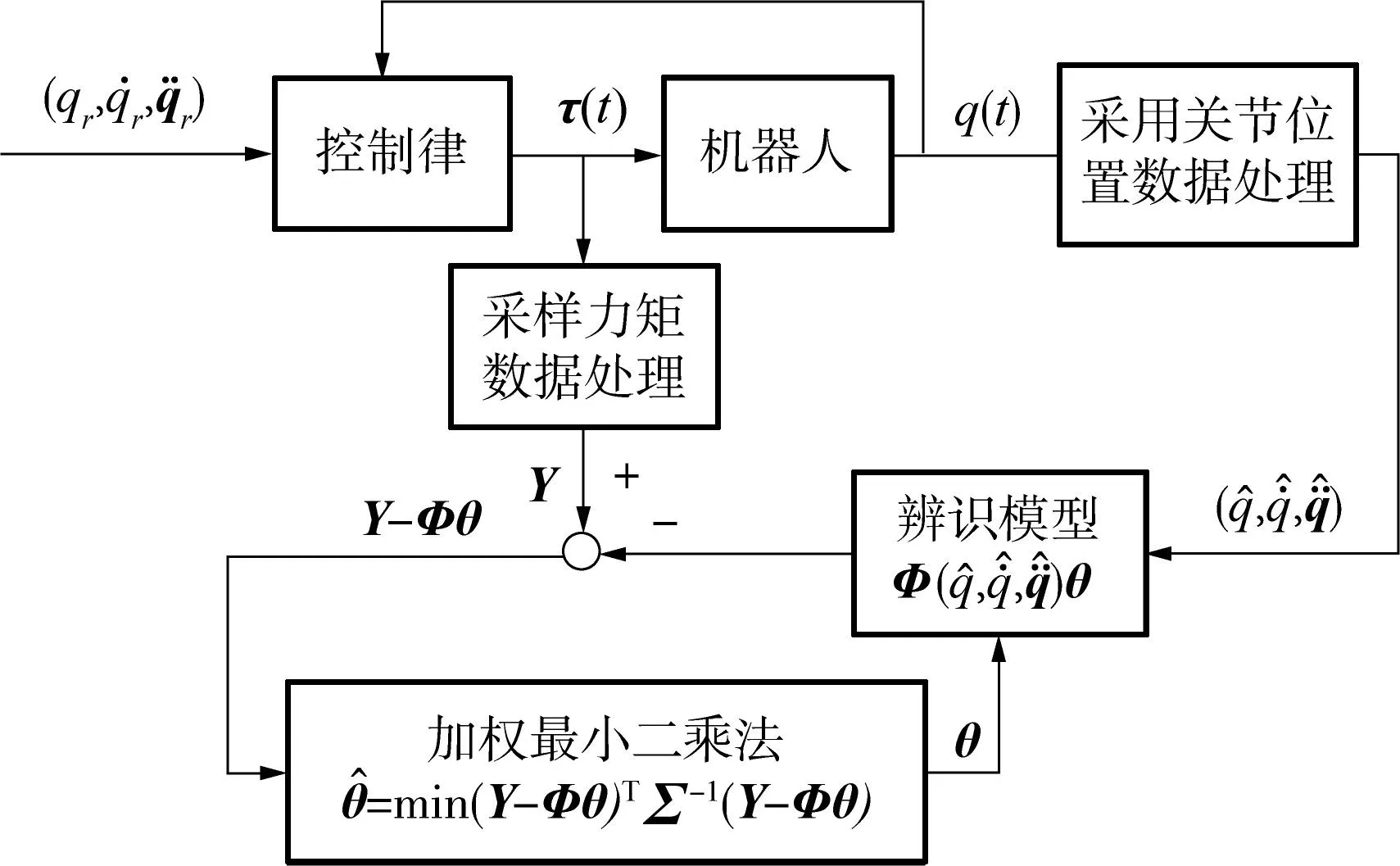
图1　机器人动力学参数辨识流程图 Fig.1　Flow chart of dynamic parameter identification of robots

2.1激励轨迹设计

未建模误差和测量数据的噪声等因素会降低辨识的精度.为提高参数估计的收敛率和抗噪声的能力，需要精心设计激励轨迹.首先要选取合适的指标函数来优化激励轨迹.文中采用文献[15]最小化观测矩阵的条件数作为轨迹优化的标准.通常，激励轨迹的设计主要考虑两个方面：①轨迹在有干扰的情况下是否能提供足够准确而快速的参数估计；②采集数据处理是否足够简单，而辨识结果又足够准确.文中采用Swevers等[16]提出的有限项周期性傅里叶级数轨迹，此轨迹由于在信号处理的种种优点而多次被应用于辨识实验.轨迹表达式为

(7)

式中：t为时间；ωf为基频；qi,0为关节位置补偿量；ai,k和bi,k分别为正弦和余弦函的幅值；D为傅里叶级数的谐波项数目，每个傅里叶级数包含2D+1个参数，分别对应于ai,kbi,kqi,0，即轨迹优化的自由度.轨迹优化受到关节位置、关节速度、关节加速度、工作空间、电机力矩等约束.因此，基于条件数优化准则的激励轨迹优化问题可描述为：

(8)

2.2采集数据的预处理

机器人跟踪激励轨迹时对关节位置和电机电流进行采集，电机电流通过转矩常数转换为电机力矩.由于所得到的数据含有一定的噪声，如果直接将采集的数据用于参数辨识，会降低辨识精度，因而需要对采集数据进行预处理.

由于文中采用的傅里叶级数轨迹所采集的数据具有周期性，因此可以通过对采集的数据进行平均化来提高信噪比[5,11]，改善数据的质量，即：

(9)

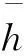
通常，关节速度和加速度无法直接测量，而对关节位置直接数值微分会放大测量中存在的噪声，因而采用文献[17]的解析法来得到角速度和角加速度.具体步骤为：①对平均化后的关节位置数据采用最小二乘法拟合成傅里叶级数；②对拟合的傅里叶级数进行求导，得到关节速度和加速度，此方法具有很好的降噪效果.

2.3参数估计方法

动力学模型(6)在机器人重复跟踪激励轨迹时，在N个时间点t1,t2,…,tN(nN>p+2n)对关节位置和电机力矩进行采样得到超静定线性方程：

(10)

式中，ΦN是nN×p的观测矩阵，N是nN×1的力矩向量，N是数据采样点.

方程(10)是个超静定线性方程，文中采用加权最小二乘法[15,17]来求解该方程，通过对测量力矩噪声协方差的逆矩阵进行加权，从而区分准确和不准确的数据来提高辨识精度.惯性参数θ的加权最小二乘估计：

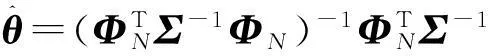
(11)

2.4模型验证

为验证辨识出的动力学参数的正确性，选取一条不同于激励轨迹的轨迹作为验证轨迹.用辨识出来的惯性参数预测验证轨迹的力矩，并对比验证轨迹力矩的测量值和预测值.实验验证过程如图2所示(me为辨识轨迹的测量力矩，为验证轨迹的测量力矩，pr为验证轨迹的预测力矩).

一般采用力矩测量值与预测值的残差均方根(RMS)来评定参数辨识的精度[5,12]:

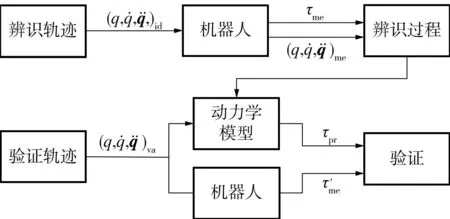
图2　实验验证流程图 Fig.2　Flow chart of experimental validation

(12)

3辨识和验证实验设计

为验证分步辨识的可行性和正确性，将实验分成5步.第1步，锁定4、5、6关节轴，驱动1、2、3关节轴跟踪辨识轨迹，辨识1、2、3连杆的惯性参数.第2步，为验证第1步辨识结果的正确性，驱动1、2、3关节轴跟踪另一条验证轨迹.用第1步辨识出的1、2、3连杆惯性参数来预测验证轨迹的力矩.第3步，为验证省略4、5、6连杆部分惯性参数对1、2、3关节力矩的影响是实际可行的，驱动全部关节轴跟踪激励轨迹，其中，1、2、3关节使用和第2步相同的轨迹，4、5、6关节可以使用任意轨迹，对比两次实验1、2、3关节力矩的差异.第4步，锁定2、3关节轴，驱动1、4、5、6关节轴跟踪辨识轨迹，辨识出4、5、6连杆的惯性参数.第5步，为对比一次性辨识方法和文中方法的辨识效果，驱动全部关节轴跟踪激励轨迹，通过比较两种方法预测力矩误差的大小说明两者的优劣.

4实验结果分析

图3所示为验证实验所用六自由度串联机器人，图4是对应的连杆坐标系.实验使用的傅里叶级数轨迹基频为0.05Hz (周期为20s)，由5项傅里叶级数组成.因此每个轨迹有11个系数需要优化，带宽为0.25Hz.数据的采样频率为1kHz，即一个轨迹周期有20000个采样数据.过多的数据会降低辨识的效率并引起不良数据的波动，因此文中从20000个采样点中等距抽取2000个点作为辨识所需的采样数据.每次实验时连续重复跟踪轨迹，等机器人的瞬态效应消失后采样50组关节位置和电机电流数据，经过处理后应用于辨识计算.表1给出了机器人的各关节的运动约束

图3　六自由度串联机器人 Fig.3　A 6-DOF serial robot

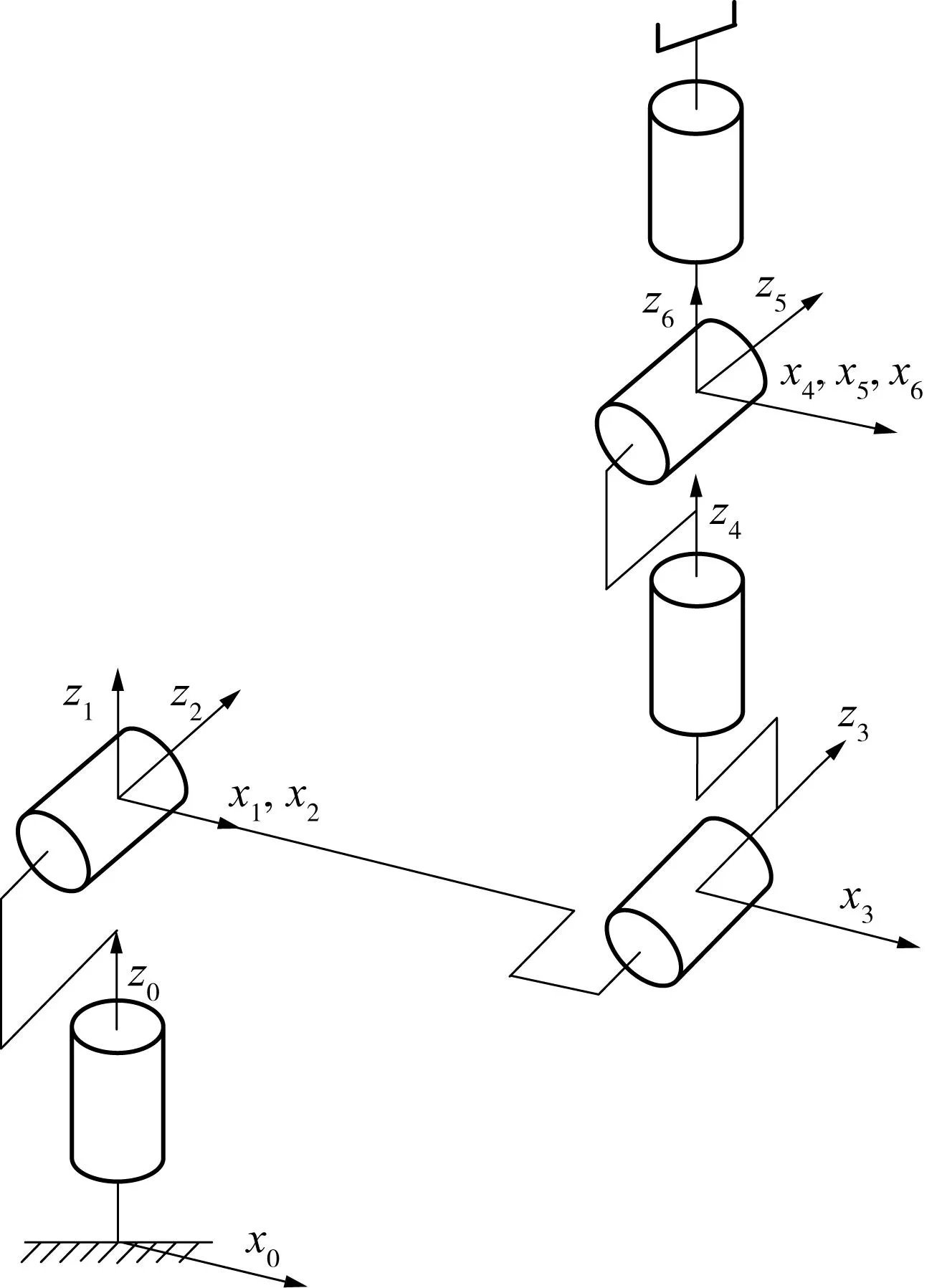
图4　机器人的连杆坐标图 Fig.4　Connecting rod the coordinate of the robot

表1机器人优化轨迹的各种约束
Table 1Constraints of robot trajectory optimization

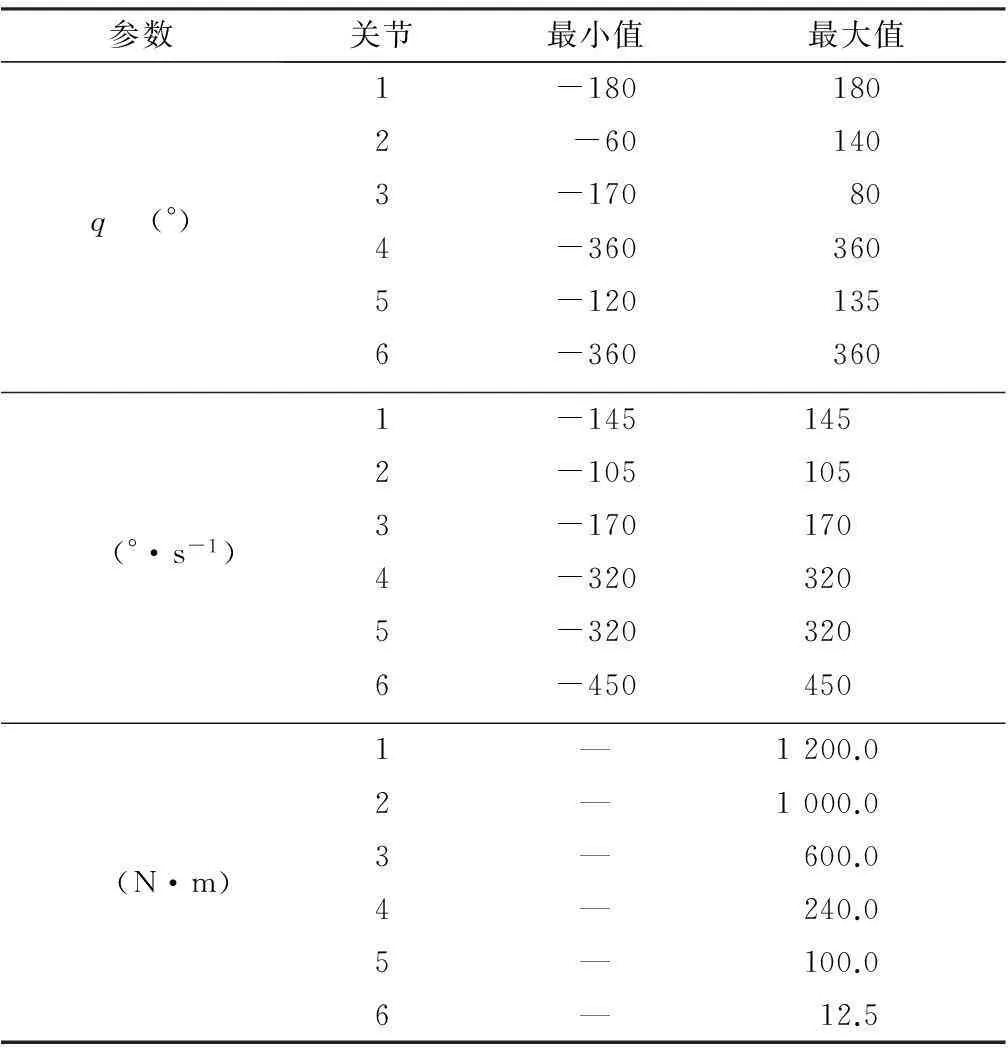
参数关节最小值最大值q(°)1-1801802-601403-170804-3603605-1201356-360360(°·s-1)1-1451452-1051053-1701704-3203205-3203206-450450(N·m)1—1200.02—1000.03—600.04—240.05—100.06—12.5

4.11、2、3关节辨识

为辨识出1、2、3连杆的惯性参数，给定1、2、3关节的激励轨迹，如图5所示 (省略其他激励轨迹).驱动1、2、3关节轴跟踪激励轨迹，辨识出1、2、3连杆的惯性参数，并比较测量力矩和预测力矩，如图6所示.由图6(c)可知，力矩预测误差小，仅在速度反转时出现误差峰值.摩擦模型在低速时无法复现复杂的动态摩擦行为可能是个关键因素.表2所示为辨识出的1、2、3连杆的惯性参数.

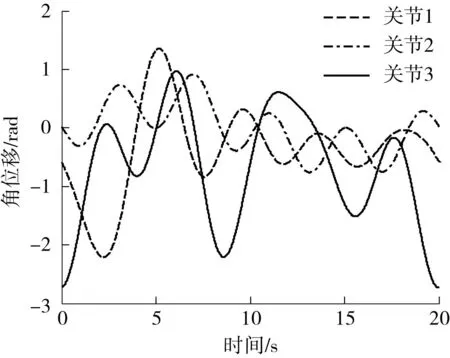
图5　1、2、3关节辨识轨迹 Fig.5　Identification trajectories of joints 1、2、3

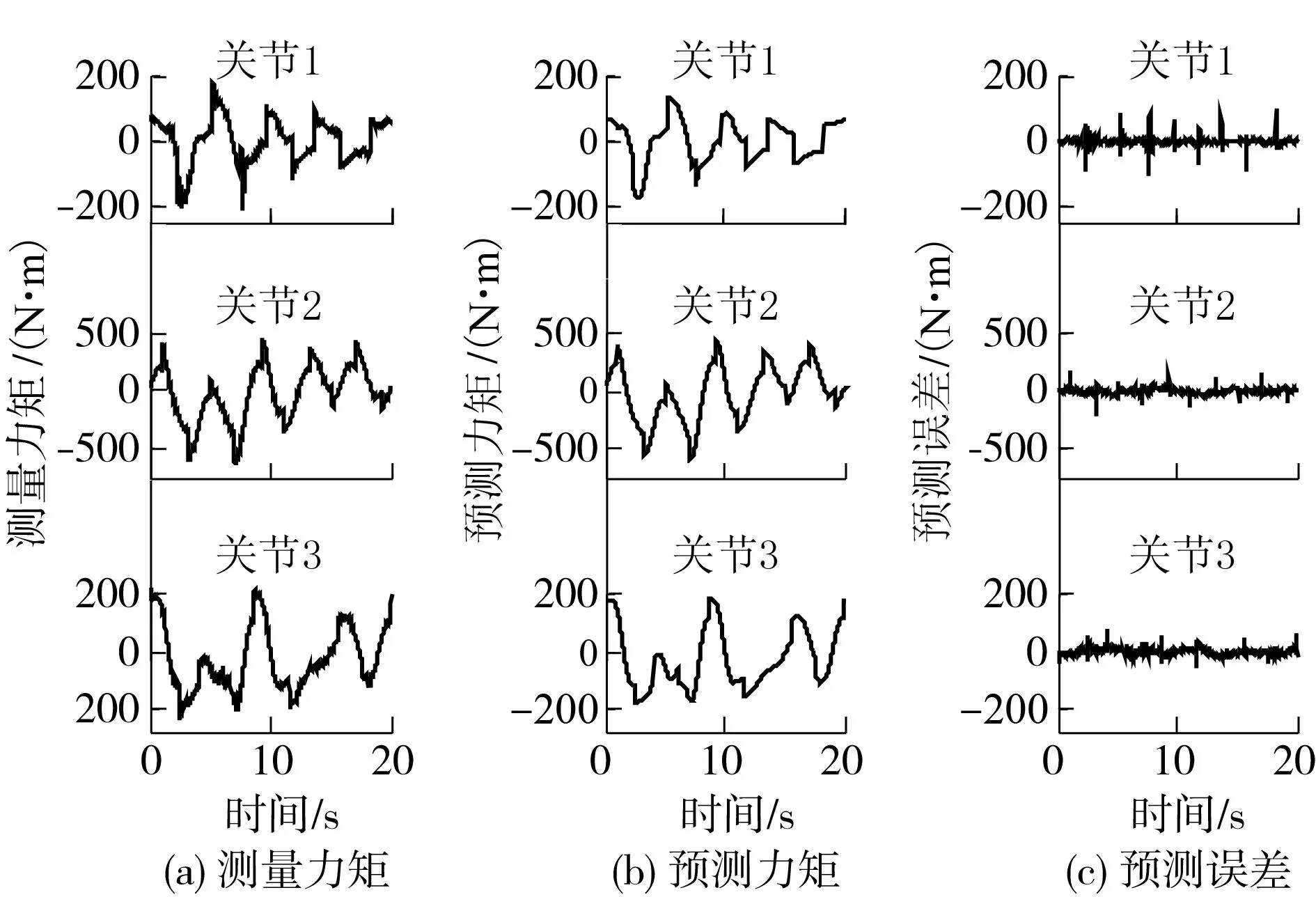
图6　1、2、3关节力矩测量值和预测值 Fig.6　Measured and predicted torques of joints 1、2、3

表21、2、3连杆的惯性参数值
Table 2Inertial parameter values of links 1、2、3

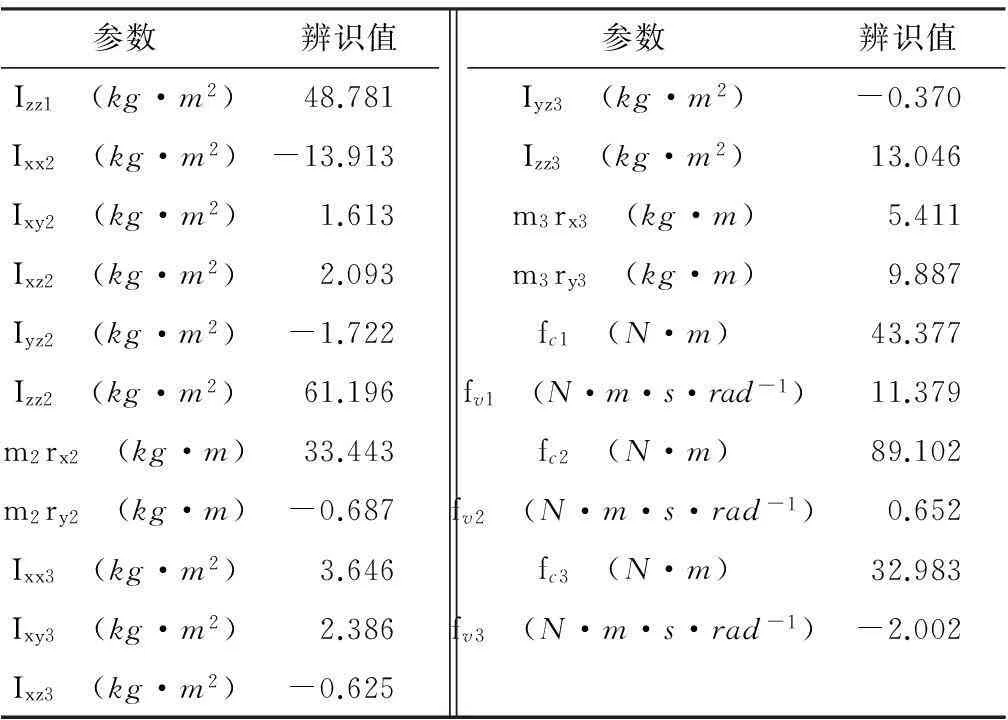
参数辨识值Izz1(kg·m2)48.781Ixx2(kg·m2)-13.913Ixy2(kg·m2)1.613Ixz2(kg·m2)2.093Iyz2(kg·m2)-1.722Izz2(kg·m2)61.196m2rx2(kg·m)33.443m2ry2(kg·m)-0.687Ixx3(kg·m2)3.646Ixy3(kg·m2)2.386Ixz3(kg·m2)-0.625参数辨识值Iyz3(kg·m2)-0.370Izz3(kg·m2)13.046m3rx3(kg·m)5.411m3ry3(kg·m)9.887fc1(N·m)43.377fv1(N·m·s·rad-1)11.379fc2(N·m)89.102fv2(N·m·s·rad-1)0.652fc3(N·m)32.983fv3(N·m·s·rad-1)-2.002

4.21、2、3关节验证

选取另一条轨迹作为验证轨迹，如图7所示.用辨识出的1、2、3连杆惯性参数来预测验证轨迹的力矩，并通过比较验证轨迹的测量力矩和预测力矩的误差来验证辨识结果.图8(c)中的力矩预测误差较小，说明辨识模型能够准确地预测机器人运动所需的力矩.

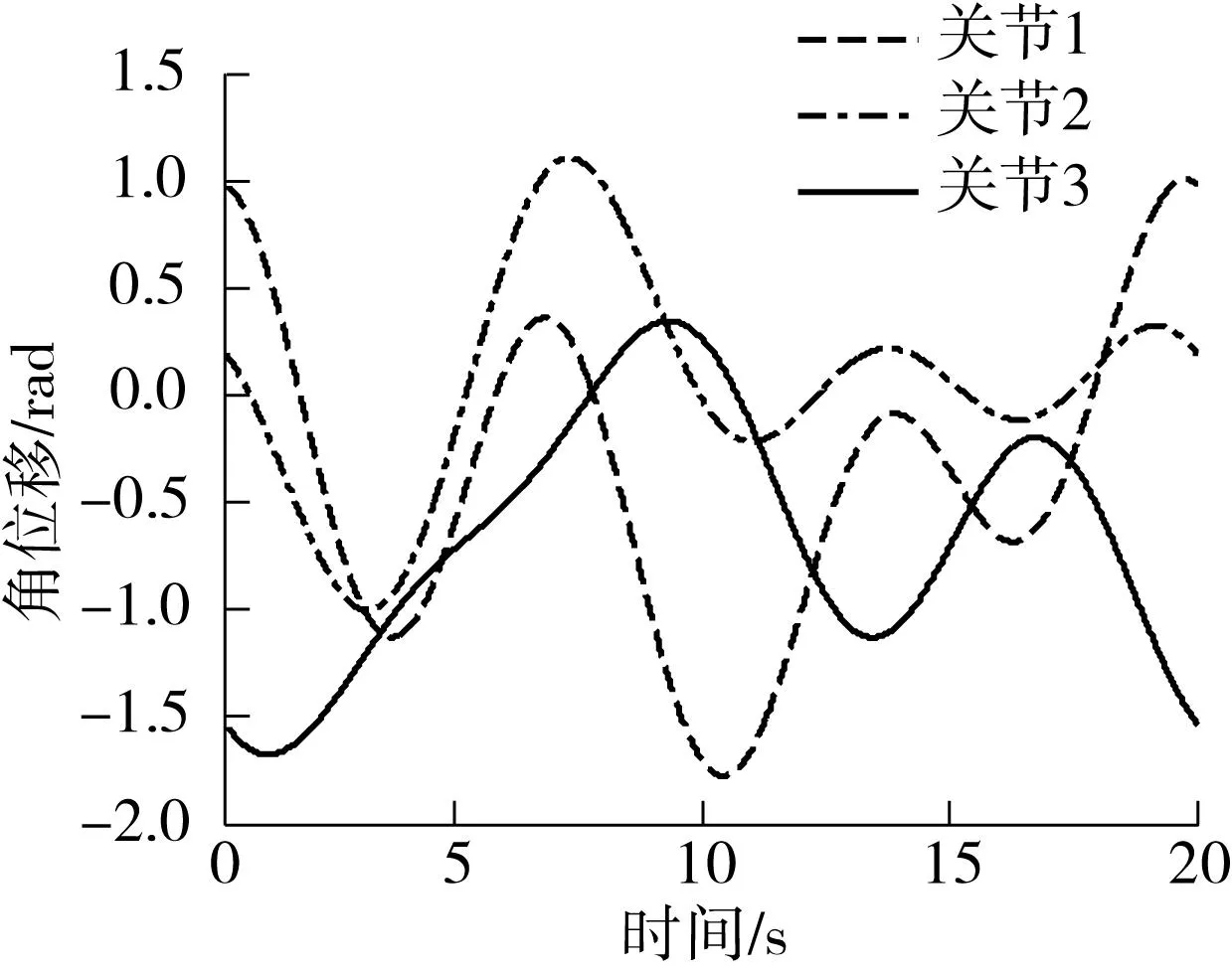
图7　1,2,3关节验证轨迹 Fig.7　Validation trajectories of joints 1,2,3

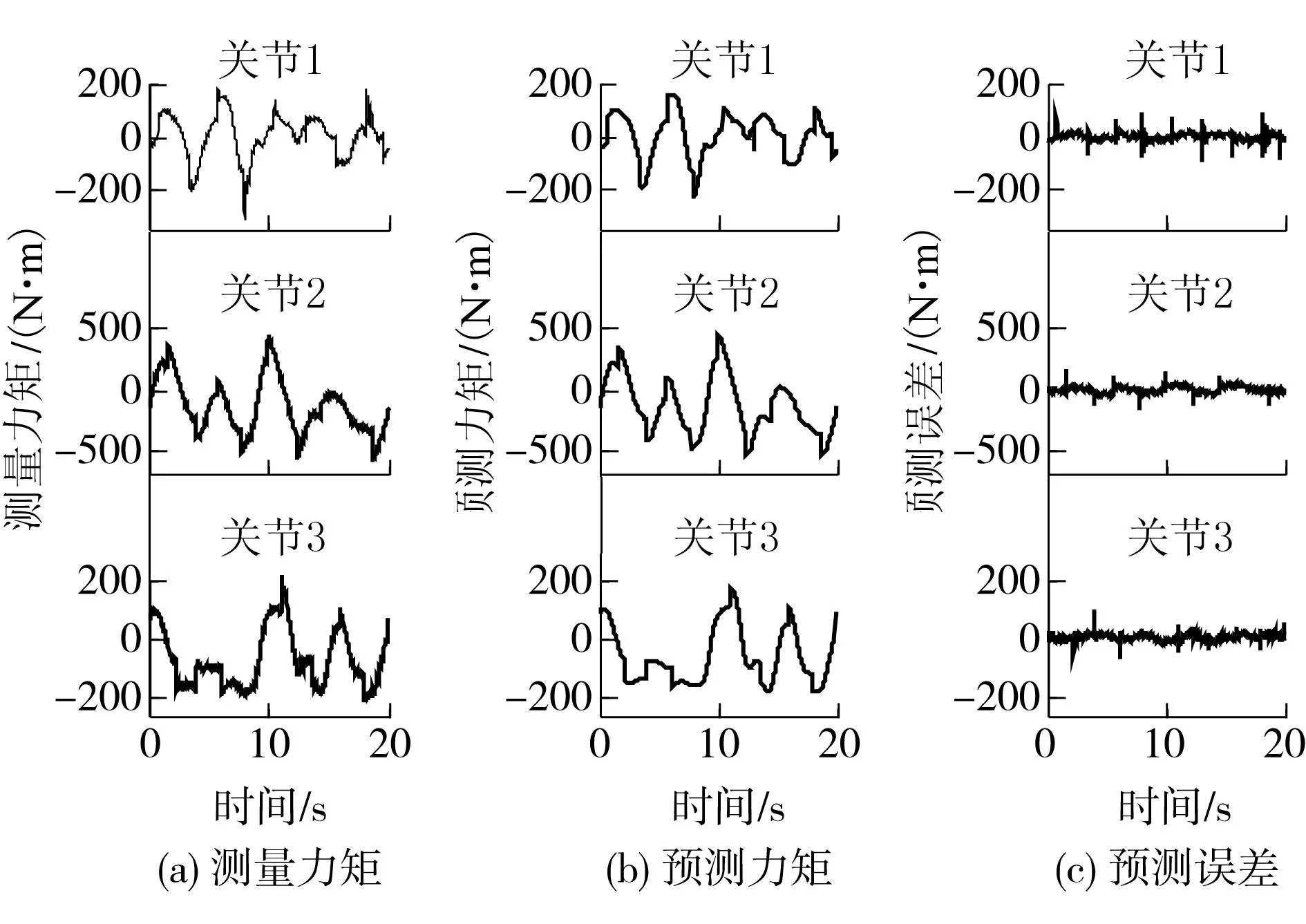
图8　1、2、3关节力矩预测的模型验证 Fig.8　Validation of the models used to predict torques of joints 1、2、3

4.3省略4、5、6连杆惯性参数的可行性

驱动全部关节轴，其中，1、2、3关节使用和前文同样的轨迹，以便对比两次实验的1、2、3关节力矩.4、5、6关节可以使用任意轨迹，但为体现4、5、6连杆惯性参数对1、2、3关节力矩的最大影响，使用具有较大速度和加速度的激励轨迹(三次项傅里叶级数轨迹).从图9的力矩对比可以看出两次实验1、2、3关节的力矩非常相近，说明省略4、5、6连杆惯性参数对1、2、3连杆力矩的影响具有实际可行性.

4.44、5、6关节辨识

驱动1、4、5、6关节轴跟踪辨识轨迹，只使用4、5、6关节力矩辨识出4、5、6连杆的惯性参数，并比较测量力矩和预测力矩.图10和表3表明：4、5、6关节辨识效果好.比较图6和图10可以看出：4、5、6关节力矩比1、2、3关节力矩小得多，体现了两者惯性参数值的差异性.表3所示为4、5、6连杆惯性参数的辨识值.对比表3和表2可以看出，1、2、3连杆惯性参数值和4、5、6连杆惯性参数值存在巨大差异性.此外，从表3可看出：4、5、6连杆的惯性参数值比摩擦系数值小很多，表现为摩擦力矩占据了大部分电机力矩，连杆惯性参数只贡献了很小的一部分电机力矩.4、5、6关节摩擦力矩对1、2、3关节力矩没有任何影响，因此4、5、6连杆惯性参数对1、2、3关节力矩的贡献很小.这进一步说明：对六自由度关节型机器人参数辨识时省略4、5、6连杆惯性参数对1、2、3关节力矩的影响是可行的.

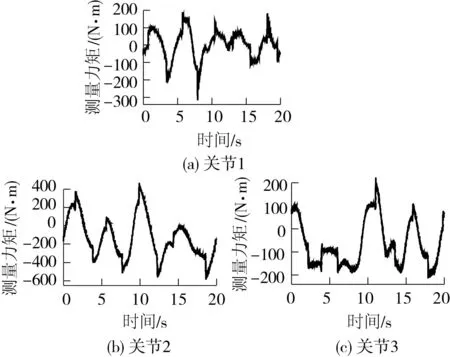
图9　两次实验1、2、3关节测量力矩对比 Fig.9　Comparison of the measured torque of joints 1、2、3 in two experiments

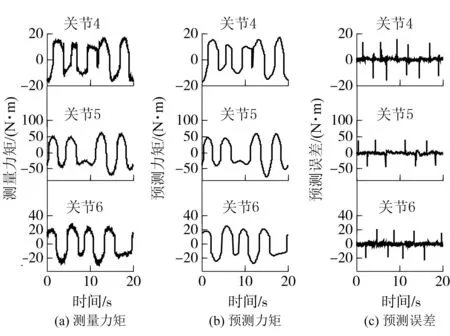
图10 　4、5、6关节力矩预测的模型验证 Fig.10　Validation of the models used to predict torques of joints 4、5、6

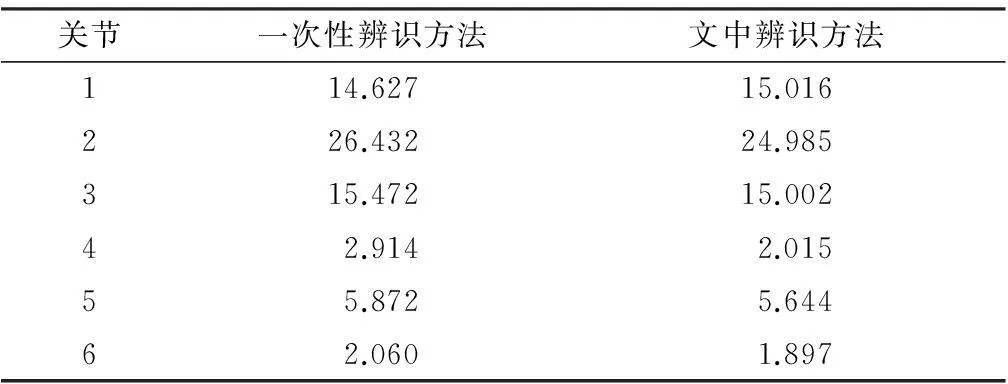
4.5分步辨识与一次性辨识方法对比

驱动全部关节轴跟踪激励轨迹，分别用分步辨识方法和一次性辨识方法的辨识结果进行力矩对比，图11、12分别为两种方法的预测力矩图.从图中可以看出，两种方法力矩预测的精度大致相同.表4对比了两种辨识方法各关节的力矩残差均方根.从表中可看出：两者大致相当，说明文中辨识方法可以得到好的估计结果.

表34、5、6连杆的惯性参数值Table 3Inertial parameter values of links 4、5、6

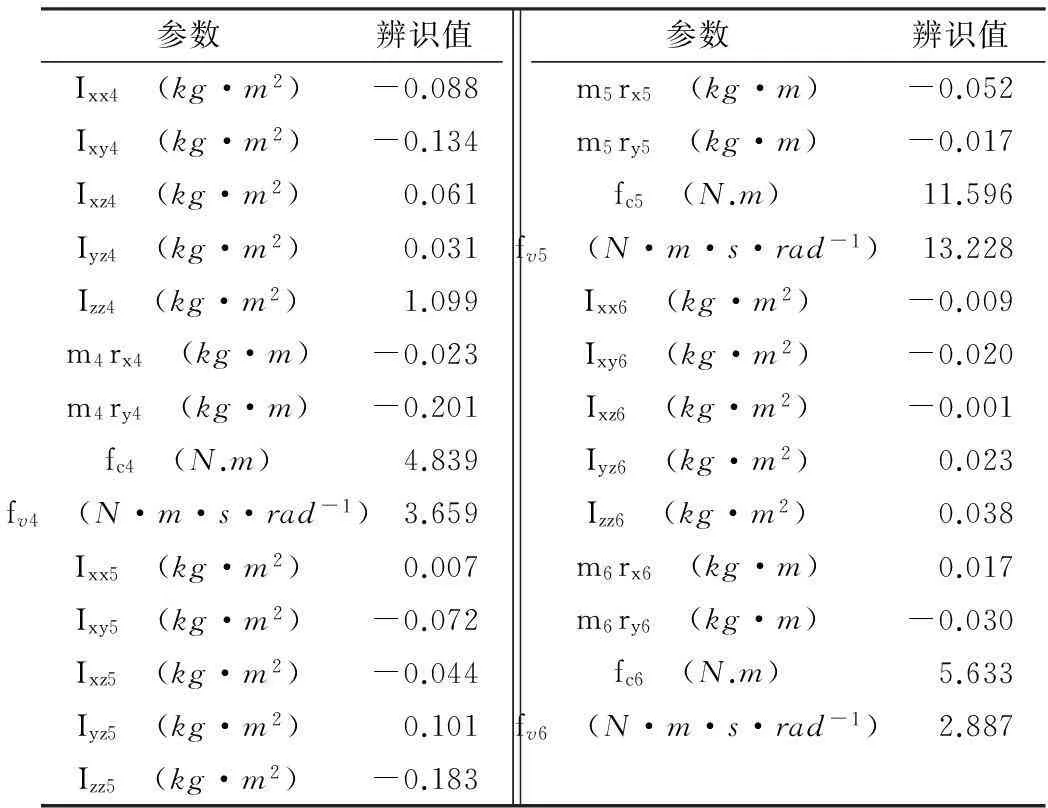
参数辨识值Ixx4(kg·m2)-0.088Ixy4(kg·m2)-0.134Ixz4(kg·m2)0.061Iyz4(kg·m2)0.031Izz4(kg·m2)1.099m4rx4(kg·m)-0.023m4ry4(kg·m)-0.201fc4(N.m)4.839fv4(N·m·s·rad-1)3.659Ixx5(kg·m2)0.007Ixy5(kg·m2)-0.072Ixz5(kg·m2)-0.044Iyz5(kg·m2)0.101Izz5(kg·m2)-0.183参数辨识值m5rx5(kg·m)-0.052m5ry5(kg·m)-0.017fc5(N.m)11.596fv5(N·m·s·rad-1)13.228Ixx6(kg·m2)-0.009Ixy6(kg·m2)-0.020Ixz6(kg·m2)-0.001Iyz6(kg·m2)0.023Izz6(kg·m2)0.038m6rx6(kg·m)0.017m6ry6(kg·m)-0.030fc6(N.m)5.633fv6(N·m·s·rad-1)2.887

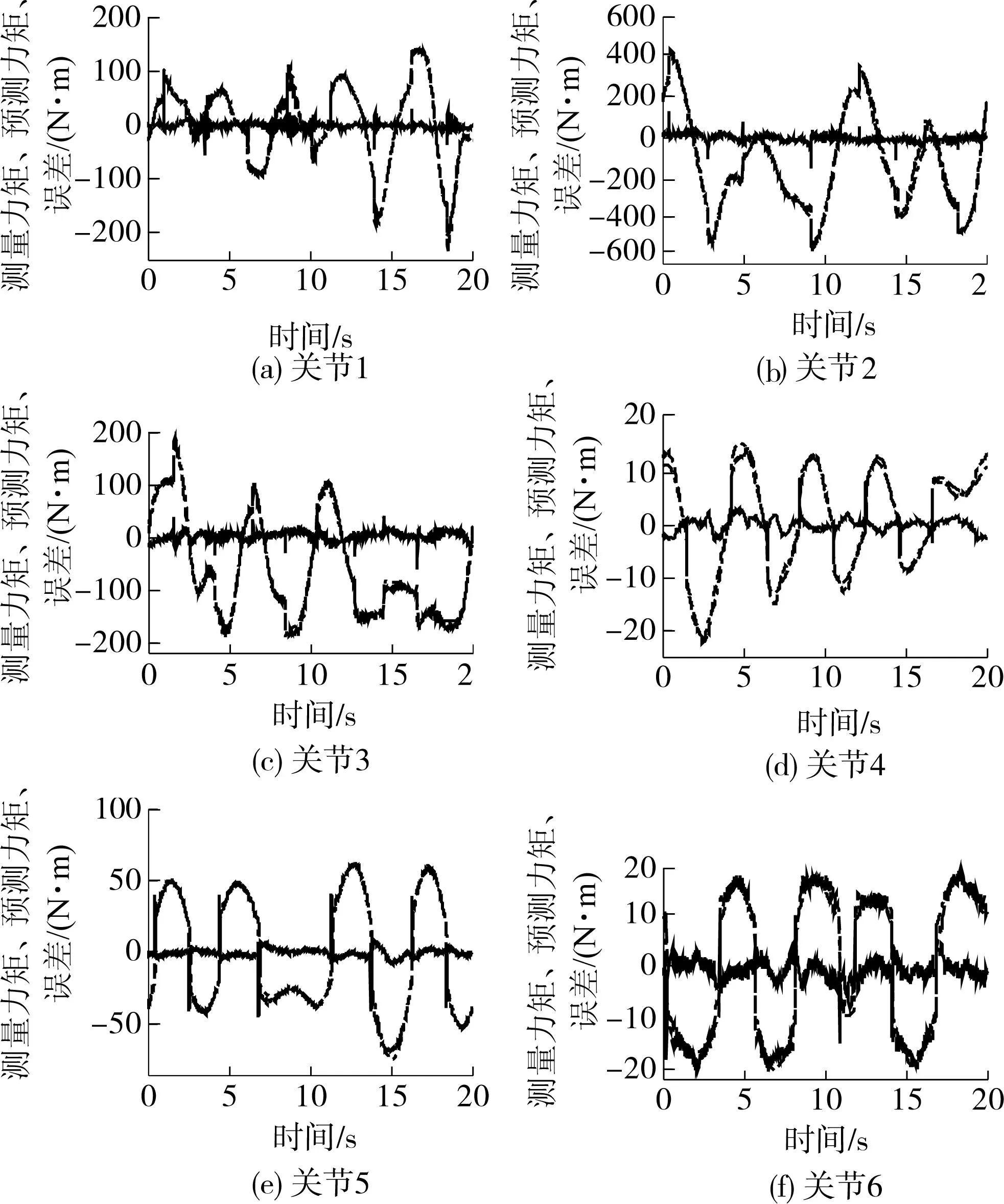
图11　一次性辨识获得的各关节预测力矩 Fig.11　Predicted torques of each joints by together identification method

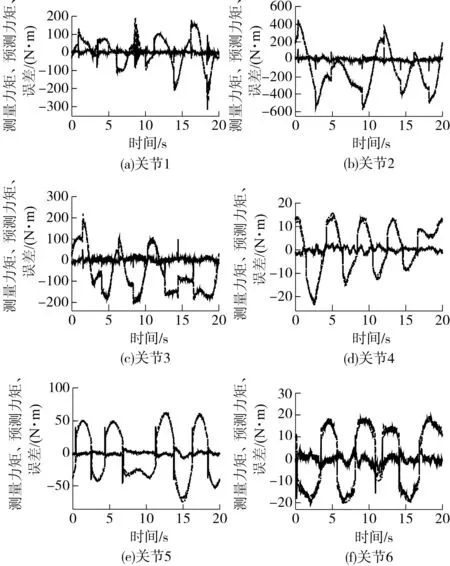
图12　分步辨识获得的各关节预测力矩 Fig.12　Predicted torques of each joints by step-by-step identification

为对比两种方法的计算效率，在同一台计算机和相同计算软件中分别完成了计算过程.计算机配置为：联想ThinkCentre E73台式机，Intel酷睿i3 4130双核处理器，2 G内存.计算软件Mathematica 8.0.在Mathematica中代入数据后求解辨识方程，得出辨识结果并给出计算时间.在文中辨识方法中，辨识1、2、3连杆惯性参数所用时间为8.917s，辨识4、5、6连杆惯性参数所用时间为24.119s，总时间为33.036s.一次性辨识方法所用时间为341.195s，约为文中辨识方法的10.3倍.可见，文中提出的辨识方法效率很高.

表4两种辨识方法的关节力距RMS对比

Table 4Comparison of RMS of joint torque by two identification methodsN·m

关节一次性辨识方法文中辨识方法114.62715.016226.43224.985315.47215.00242.9142.01555.8725.64462.0601.897

5结论

针对机器人动力学参数辨识的问题，在综合了一次性参数辨识和已有分步辨识方法后，提出了针对性的分步辨识方法，将肘关节和腕关节进行两次辨识，两次辨识得到机器人全部惯性参数.该方法大大简化了辨识模型，降低了辨识的难度，可行性好，辨识更具有针对性.文中设计了针对特定六自由度关节机器人1、2、3连杆惯性参数的辨识算法及实验，关节预测力矩与测量力矩结果对比显示：

(1)文中提出的方法能正确辨识相关惯性参数，依据辨识结果能高效、准确地实现对关节驱动力矩的预测.

(2)在辨识1、2、3连杆惯性参数时，忽略4、5、6连杆对1、2、3连杆的影响是可行而有效的.对于大多数腕关节惯性参数值较小的工业机器人来说，相对于一次性辨识所有连杆惯性参数，忽略关节4、5、6连杆惯性参数将更利于实现基于动力学模型的机器人控制.

参考文献：

[1]Wu Jun,Wang Jin-song,You Zheng.An overview of dynamic parameter identification of robots [J].Robotics and Computer-Integrated Manufacturing,2010,26(5):414-419.

[2]Brogardh T.Robot control overview:an industrial perspective [J].Modeling Identification and Control,2009,30(3):167-180.

[3]刘楚辉，姚宝国，柯映林．工业机器人切削加工离线编程研究 [J]．浙江大学学报：工学版，2010,44(3):426-431.

Liu Chu-hui,Yao Bao-guo,Ke Ying-lin.Study on off-line programming of industrial robot for cutting process [J].Journal of Zhejiang University:Engineering Science,2010,44(3):426-431.

[4]Qin Z K,Baron L,Birglen L.A new approach to the dynamic parameter identification of robotic manipulators [J].Robotica,2010,28(4):539-547.

[5]Swevers J,Verdonck W,Schutter D S.Dynamic model identification for industrial robots [J].IEEE Control Systems Magazine,2007,27(5):58-71.

[6]Rosillo N,Valera A,Benimeli F,et al.Real-time solving of dynamic problem in industrial robots [J].Industrial Robot:An International Journal,2011,38(2):119-129.

[7]Atkeson C,An C H,Hollerbach J M.Estimation of inertial parameters of manipulator loads and links [J].The International Journal of Robotics Research,1986,5(3):101-119.

[8]Dutkiewicz P,Kozlowski R K,Wroblewski W S.Experimental identification of robot and load dynamics parameters[C]∥Proceedings of the 2th Conference on Control Applications.Vancouver:IEEE,1993:767-776.

[9]Vandanjon P O,Gautier M,Desbats P.Identification of robots inertial parameters by means of spectrum analysis[C]∥Proceedings of the 1995 International Conference on Robotics and Automation.Nagoya:IEEE,1995:3033-3038.

[10]Daemi M,Heimann B.Separation of friction and rigid body identification for an industrial robot[C] ∥Proceedings of the 12th CISM-IFToMM Symposium on the Theory and Practice of Robots and Manipulators.Paris:IEEE，1998:35-42.

[11]Vuong N D,Ang M H.Dynamic model identification for industrial robots [J].Acta Plolytechnica Hungarica,2009,6(5):51-68.

[12]Calanca A,Capisani L M,Ferrara A,et al.MIMO closed loop identification of an industrial robot [J].IEEE Transactions on Control Systems Technology,2011,19(5):1214-1224.

[13]Grotjahn M,Daemi M,Heimann B.Friction and rigid body identification of robot dynamics [J].International Journal of Solids and Structures,2001,38(10):1889-1902.

[14]Benimeli F,Mata V,Valero F.A comparison between direct and indirect dynamic parameter identification methods in industrial robots [J].Robotica,2006,24(5):579-590.

[15]Bingul Z,Karahan O.Dynamic identification of Staubli RX-60 robot using PSO and LS methods [J].Expert Systems with Applications,2011,38(4):4136-4149.

[16]Swevers J,Ganseman C,Tukel D B,et al.Optimal robot excitation and identification [J].IEEE Transactions on Robotics and Automation,1997,13(5):730-740.

[17]Kinsheel A,Taha Z,Deboucha1 A,et al.Robust least square estimation of the CRS A465 robot arm’s dynamic model parameters [J].Journal of Mechanical Engineering Research,2012,4(3):89-99.

An Identification Method of Industrial Robot’s Dynamic Parameters

DingYa-dongChenBaiWuHong-taoShenHao-yu

(Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology, Nanjing University of Aeronautics and Astronautics,

Nanjing 210016, Jiangsu, China)

Abstract:As the identification equations for robots’dynamic parameters become very complicated with the increase of joints, it is difficult to obtain accurate equations of dynamic parameters when a robot is of more than four joints. In order to solve this problem, a step-by-step identification method is proposed. In this method, less inertial parame-ters should be identified in each step, which results in simpler identification equation, more efficient calculation and smaller accumulative error. Therefore, the parameter estimation can be achieved quite well for the robots with more than four joints. In order to validate the effectiveness of the proposed step-by-step identification method, a robot with six degrees of freedom is taken as an object to conduct the corresponding identification experiments. The results demonstrate that the proposed method is a simple but effective way to obtaining the key dynamic parameters of robots without changing their key dynamic characteristics.

Key words: industrial robot; dynamic parameter; step-by-step identification; identification algorithm; trajectory optimization

Foundation item: Supported by the National Natural Science Foundation of China(NSFC)(61471173)