硅压力传感器基座受力变形时的输出性能

硅压力传感器基座受力变形时的输出性能*

胡国清1龚小山1周永宏2邹崇2Jahangir Alam1

(1.华南理工大学 机械与汽车工程学院， 广东 广州 510640；

2.福建上润精密仪器有限公司， 福建 福州 350015)

摘要：为分析硅压力传感器基座受力变形对传感器输出性能的影响，首先利用弹性力学理论和板壳理论分析推导了压力传感器方形膜片应力分布,为力敏电阻在应变膜上的布置提供依据；再利用ANSYS进行分析模拟,探究了传感器基座结构变形对应变膜应力差的影响；然后针对减小基座受力变形对芯片受力的影响,对基座结构进行适当优化,并对比仿真分析的结果；最后通过实验测得优化前后的传感器输出数据.结果表明，传感器基座结构优化后，传感器硅芯片中心最大变形量从2.172μm降低到1.819μm，输出误差从0.95%下降到0.60%.

关键词：压力传感器；硅传感器；输出性能；有限元分析；结构优化

中图分类号：TH86

doi：10.3969/j.issn.1000-565X.2015.03.001

文章编号：1000-565X(2015)03-0009-06

收稿日期：2014-09-04

基金项目：* 国家自然科学基金资助项目(51175184)

作者简介：曹彪(1963-)，男，教授，博士生导师．主要从事数字化电源设备及智能控制研究．E-mail: mebcao@scut.edu.cn

目前硅压阻式压力传感器技术是传感器行业一项逐渐成熟的技术,硅压力传感器是微机电系统(MEMS)设备中主要的应用之一[1-2]；但其对精度和稳定性的要求比以往更加严格.

近年来,国内外广泛开展了关于硅压阻式压力传感器的研究以及针对热应力、封装应力、静压力等对传感器性能的影响来对压力传感器进行优化设计的研究.Bakhoum、Ferreira等[3-4]研究了能承受10MPa左右静压、测量范围为0.01～1.00MPa的硅压阻式压力差压传感器，并从边缘长度与厚度之比方面对传感器方膜片进行优化设计；据机械压力的不对称、方膜片面积与厚度之比及大量微机械工艺来设计压阻敏感部件的最优位置.Tsouti等[5]通过建立传感器芯片整体(包括基座、中间层等)的模型研究了结构参数对微机械电容式压力传感器性能的影响.Chou等[6]采用有限元方法研究了热应力和封装应力对硅基压阻式压力传感器的灵敏度和稳定性的影响.沈艳婷等[7]研究了静压对金属电容式差压变送器测量精度的影响,针对100、200、300、400kPa差压做了静压值为1、2、3、4MPa的静压测试,并用数学方法对输出结果进行修正.

硅压力传感器是一种发展很快的压阻式压力传感器，其采用了硅-硅直接键合和浓硼自终止腐蚀等技术,并将压敏电阻以惠斯通电桥的形式布置于硅应变膜上[8].文中首先利用弹性力学理论和板壳理论分析推导了方形膜片的应力分布；硅压力差压芯片中间较薄部分即硅杯底部可视为方形膜片，是主要承受压力并产生变形的部位；然后通过有限元分析软件ANSYS进行分析模拟,指导压敏电阻的位置布置，此时是单独分析硅芯片；之后探讨基座受力变形对芯片受力的影响，此时是分析粘接在基座上的硅芯片,对基座结构进行适当优化,并对比仿真分析的结果；最后对比实验测得的优化前后的传感器输出数据[9].在精度要求较高的情况下,传感器安装基座的变形对硅压力芯片的分布应力及变形量有直接影响,并达到了不能忽略的数量级,故文中在传感器应力分析时不仅对硅压力芯片进行分析模拟,还将传感器安装基座的受力变形考虑在内,最后以减小基座受力变形对芯片受力的影响为目的对基座结构进行了适当优化.

1方形膜应力分布理论分析

设方形膜片尺寸为a×b×h,如图1所示,在受到均匀压力p且周边固支的情况下,若绕度远小于膜片厚度,可认为满足小绕度理论.结合薄板弯曲理论,薄板内弯曲应力为：

(1)

式中：w为膜上任一点(x,y,z)绕度,z为以应变膜中面为xOy面的任一点竖坐标；σx为方膜横向应力；σy为方膜纵向应力；E、μ为材料弹性模量和泊松比.

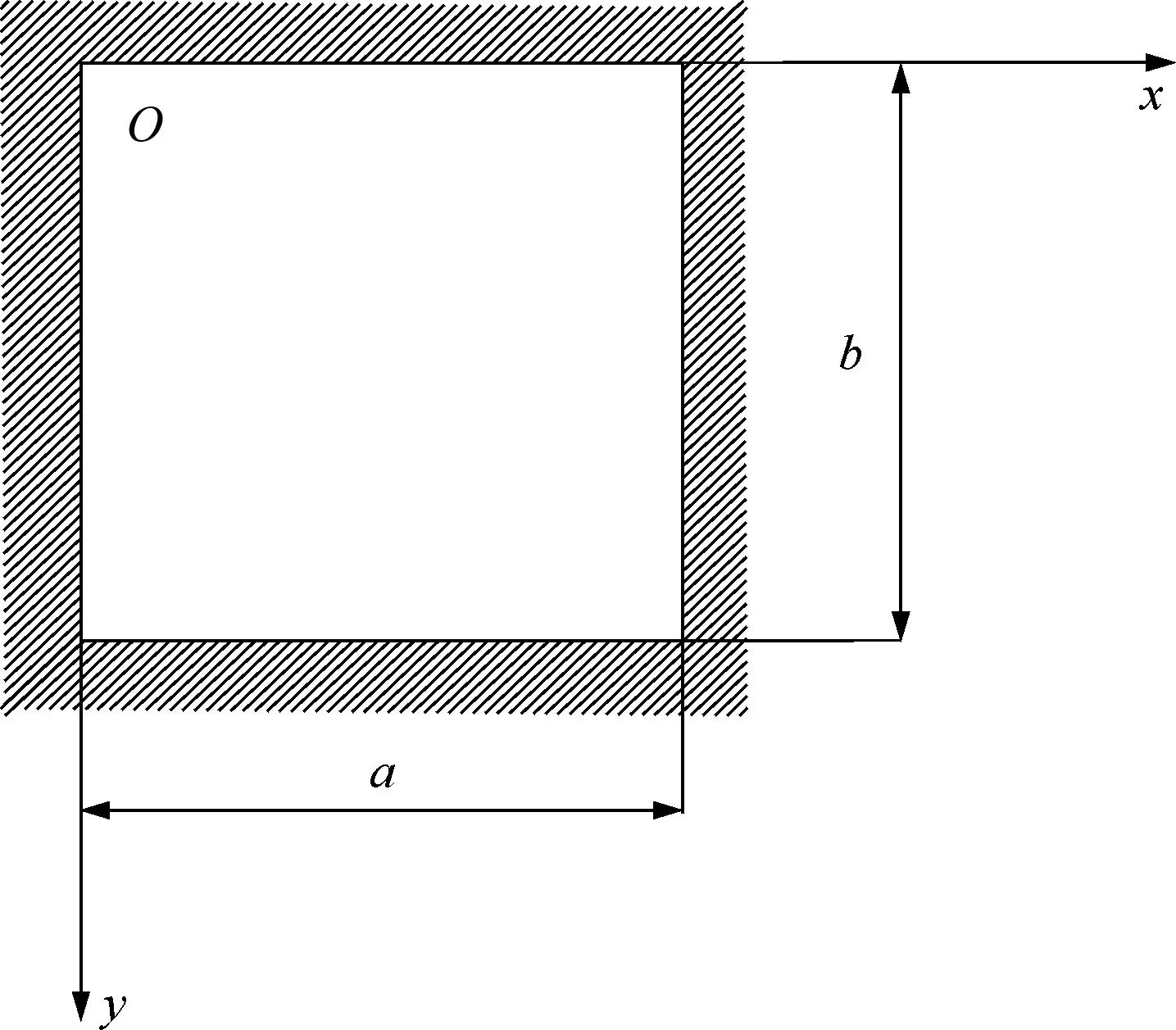
图1　四边固支方形膜片 Fig.1　Four edges-fixed support square diaphragm

采用里兹法求解均布载荷下的四边固定方形板的绕度w[10].

边界条件为：

(2)

选取

以满足边界条件.式中Kmn为x、y无关的常量.

由最小势能原理,计算得

(3)

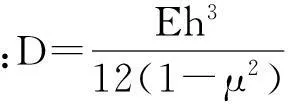
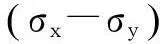
(4)

(5)

2硅片结构应力的有限元仿真分析

文中使用的压力传感器硅芯片通过阳极键合,将由腐蚀法获得的硅杯固定在硅基座上.硅杯底部为压力敏感部位,其受力变形会使布置其上的压敏电阻(构成惠斯登电桥)阻值发生变化,反映到传感器输出.故将压敏电阻布置在硅杯底部应力最大的部位即可获得最大的传感器灵敏度[11].以下采用有限元分析软件ANSYSworkbench对硅杯进行受力分析,从而得到压力敏感部位的应力分布情况.

2.1应力计算数学模型的建立

硅杯结构示意图如图2所示,应变膜部分几何特点如图3所示.硅片为正方形,具体结构参数为L×L=2.15mm×2.15mm、T=0.39mm；其中，L为外周边长，T为外周厚度.根据硅杯腐蚀工艺特点,由硅的各向异性腐蚀所得到的腐蚀角α=54.74°,硅杯上应变膜部分厚度t=0.09mm,底脚宽a=0.36mm,计算得边长l=1.001mm(此时l=a=b).由硅片受力为均匀压力及其结构的对称性,为节约计算时间及方便观察结果,将分析模型简化为其四分之一进行建模[12].相关材料参数如下：不锈钢的杨氏模量为193GPa，泊松比为0.31；硅的杨氏模量为190GPa，泊松比为0.28[13].选取1/4区域分析时,边界条件为：

(6)

图2　硅杯结构示意图 Fig.2　Sketch of silicon wafer structure

图3　直角坐标系中的薄板 Fig.3　Thin plate in a rectangular coordinate

式中θ为膜上任上一点转角.

2.2ANSYS仿真计算

建立好模型后,采用三维六面体单元网格对其划分网格，如图4所示.模型被划分为228480个节点,60628个单元.对模型的底面施加固定约束,两侧面施加对称约束.对模型上表面施加大小为1MPa、方向竖直向下的均布载荷[14].结果如图4、5所示.

图4　1/4硅杯模型网格划分 Fig.4　Meshing of a 1/4 silicon cup model

由图5(a)可知,弹性膜发生最大变形的位置是其正中心位置,与理论分析得出的结果一致；由图5(b)可知，弹性膜应力最大的位置是应变膜的边缘位置及中心,即等效应力云图中深色区域.

根据单晶硅的压阻效应,当力敏芯片应变膜发生应变时,惠斯登全桥(桥臂电阻均为RB)上各电阻条阻值变化率为[15]：

(7)

由图6可看出，应力差最大值位于中心到边缘约0.537mm处,即应变膜片四周中间处应力差最大,为19.7MPa；故在该区域布置力敏电阻时,可以获得最高的灵敏度.

(a)硅杯变形云图

(b)等效应力云图 图5　1/4硅杯变形与等效应力云图 Fig.5　Deformation and equivalent stress nephograms of 1/4 silicon cup

图6　单独分析硅片沿中心到边缘路径上纵横应力差值的分布曲线 Fig.6　Distribution curves of the vertical and horizontal stress difference on the path along the center to the edge of a separate-analysis silicon wafer

为分析基座变形对硅芯片表面中线纵横应力差值的影响,应用相同边界条件及约束(由基座的结构对称性,取1/2模型分析)仿真分析贴合在传感器基座安装位置后的硅芯片表面中线纵横应力差值.结果如图7所示：应力差最大仍发生在应变膜片中心至边缘的中心区域,但最大值约3.7MPa,较单独分析硅片时明显减小,反映到应变电阻上后将影响传感器输出.

图7　贴合到基座上硅片沿中心到边缘路径上纵横应力差值的分布曲线 Fig.7　Distribution curves of the vertical and horizontal stress difference on the path along the center to the edge of the silicon wafer fit to the base

3与硅芯片粘接的基座的结构优化设计

硅片通过结构胶贴在基座压力腔表面中心,考虑到硅差压传感器中与硅芯片粘接的基座(硅芯片与基座贴合)在受到压力时产生变形,继而对与之相连的硅芯片产生影响,因此需要对基座的受力进行分析,并以减少与硅芯片相连接部位的变形为目标,对基座结构进行合理的优化.

采用ANSYS有限元分析软件对基座进行有限元仿真分析,仿真时删除小尺寸圆角和倒角等不影响计算模型精度的小特征以简化模型为轴对称结构,得出基座变形云图.压力腔中由基座底部中心指向边缘路径的变形如图8所示，最大变形量值如图9所示,可见远离基座中心的位置相对于中心位置的变形较小.故减小在静压力作用下的与硅芯片贴合部位的变形就可以减小与之贴合的芯片的变形,从而减小静压对传感器输出的影响.

3.1硅芯片与基座组件的有限元仿真对比

将硅芯片的安装简化为直接键合在基座底部中心孔位置,简化后基座部分小特征(如尺寸较小的倒角)同样由结构的对称性取1/2结构进行分析.硅芯片网格划分方法设置为Hex Dominant(六面体主导),单元尺寸设置为0.1mm；基座形状不规则,故使用网格划分方法Tetrahedrons(四面体网格),单元尺寸设置为0.3mm.最后划分的单元数为103854,使用单元畸变度Skewness网格质量衡量准则查看网格质量，单元畸变度平均为0.22,网格质量合格.如图10所示.优化前后组件的等效应力见图11.

图8　10MPa压力下基座底部中心指向边缘路径的变形图 Fig.8　Deformation nephogram of the base bottom path along the center to the edge under 10MPa

图9　10MPa压力下基座中心指向边缘路径的总体变形曲线 Fig.9　Deformation curve of the base bottom path along the center to the edge under 10MPa

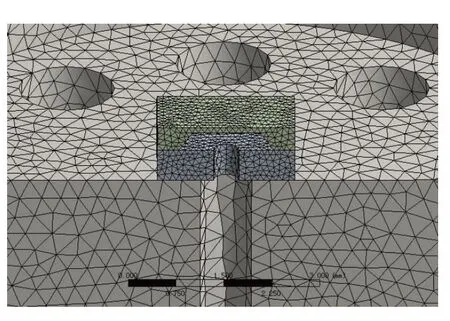
图10　硅芯片与基座组件网格划分 Fig.10　Meshing of the silicon chip and base components

基座与端座之间以氩弧焊工艺焊接,故与端座连接的部位可视为固定约束,硅油传递过来的压力视为均布载荷施加在充油部位,包括硅片各浸油表面.拟加载静压力为10MPa.仿真得最大等效应力为146.55MPa(见图12(a)),发生在基座的固定约束位置,最大变形量为2.172μm(见图13(a)),发生在硅片中心位置.

(a)优化前

(b)优化后

Fig.11Stress nephogram contrast of the assembly before and after optimization

为了减小硅片因基座受力变形产生的应力增大的效应,现将硅片的安装结构进行优化.采用去掉基座与芯片贴合部位周围部分材料的方法,在基座中心加工外径为4.50mm、内径为3.20mm、深度为0.50mm的环形槽,对基座进行优化.优化前后组件的结构及实物见图14.

使用ANSYS-WorkBench作仿真,并通过实验进行验证.优化前后仿真结果对比见图11-13.发现硅芯片中心为最大变形位置,最大变形量为1.819μm(见图13(b)),最大等效应力为167.43MPa(见图12(b)).因最大等效应力发生的位置在固定基座的边缘处,实际加工时采用氩弧焊焊接在传感器端座上,对芯片的影响不大.在最大变形量上优化后比优化前小,即优化可以减小硅片因基座受力变形产生的应力变化,这对于提高压力传感器的精度而言有实际意义.

(a)优化前

(b)优化后

图12优化前后组件中硅芯片的等效应力分布对比

Fig.12Stress nephogram contrast of the chip on the assembly before and after optimization

(a)优化前

(b)优化后

图13优化前后组件的总体变形云图对比

Fig.13Deformation nephogram contrast of the assembly before and after optimization

Fig.14Sketch and photos of the assembly before and after optimization

3.2实验结果对比分析

分别对10个传感器优化前(未加工环形槽)和优化后(加工环形槽)的状况进行测试，编号分别为A1-A10,测出传感器满量程实际输出电压值.测试装置包括：双通道压力校准仪(精度等级为0.01%)、精密数字电流电压表(精度等级为0.01%)、稳压电源、三阀组、高压气管、带减压阀的氮气源2瓶(≥10MPa).实验过程如下：①设备自动校准，即压力校准仪双通道分别自动调零；②检测密封性；③双向静压试验.对于A、B通道分别施加相同10MPa静压后，保持高压端A压力不变，按差压值(以40kPa差压为例，差压值按0、10、20、30、40kPa选取，共5个等级)将B通道上压力逐步减小一个步距10kPa，记录输出电压值.测试结果如表1所示.

由表2可知,优化后的传感器输出数据与理论值之差较优化前小,优化后此差值最大为0.163V,而优化前的传感器输出数据与理论值之差最大为0.195V,即优化后传感器输出数据更加趋于合理.因为后续的线性校正过程,笔者只对比零点(理论输出为3V)时输出数据与理论值的绝对误差,其中，

表1优化前后传感器测试输出电压值
Table 1Sensor test output before and after optimization

序号优化前/后测试值/V11)21)31)41)51)A1优化前1.1032.1022.9763.9254.869优化后1.1532.0753.0063.9374.869A2优化前1.1302.0612.9933.9404.878优化后1.1402.0662.9993.9324.866A3优化前1.1392.0713.0033.9424.882优化后1.1362.0632.9983.9334.869A4优化前1.1332.0663.0073.9474.886优化后1.1242.0613.0043.9404.893A5优化前1.1342.0693.0043.9464.887优化后1.1192.0542.9983.9414.894A6优化前1.1312.1152.9723.9384.872优化后1.1482.0733.0063.9454.880A7优化前1.1102.1012.9833.9254.876优化后1.1482.0783.0123.9474.884A8优化前1.1032.1052.9773.9274.887优化后1.1342.0663.0063.9464.887A9优化前1.1102.1152.9783.9354.872优化后1.1632.0863.0183.9374.872A10优化前1.1122.1952.9753.9344.871优化后1.0522.0673.0033.9414.879

1)1-5表示理论值，下同.

表2优化前后测试值与理论值之差
Table 2Difference between the test values with the theoretical values before and after optimization

序号优化前/后相对误差/V12345A1优化前0.1030.1020.0240.0750.131优化后0.1530.0750.0060.0630.131A2优化前0.1300.0610.0070.0600.122优化后0.1400.0660.0010.0680.134A3优化前0.1390.0710.0030.0580.118优化后0.1360.0630.0020.0670.131A4优化前0.1330.0660.0070.0530.114优化后0.1240.0610.0040.0600.107A5优化前0.1340.0690.0040.0540.113优化后0.1190.0540.0020.0590.106A6优化前0.1310.1150.0280.0620.128优化后0.1480.0730.0060.0550.120

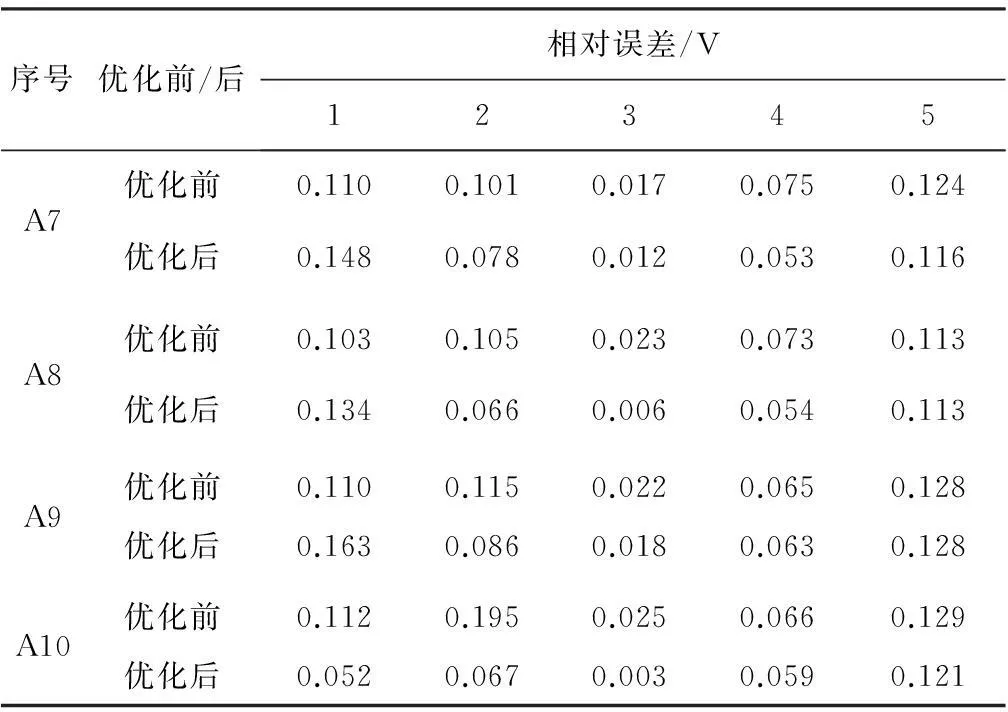
续表2

优化前后实验结果如图15所示，优化后绝对误差最大为0.60%,比优化前的0.95%小,且优化后绝对误差曲线均在优化前绝对误差下方,说明优化后的输出数据更加接近于理论值,后续的校正过程带去的误差有所减小.

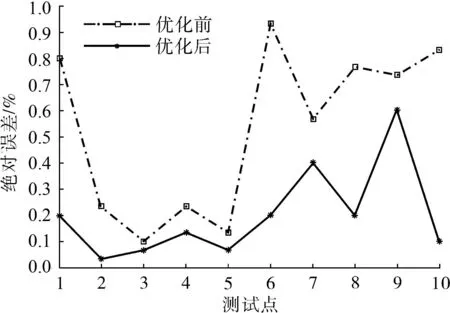
图15　优化前后实验结果对比 Fig.15　Comparison of test results before and after optimization

4结论

文中利用弹性力学和板壳理论推导了方形平膜片的受力,并利用ANSYS软件进行仿真模拟；为使所制作的传感器得到最大的灵敏度,压敏电阻应布置在方形膜边缘中间位置.并以减小基座中心变形为目标对基座的结构进行优化,对比分析优化前后的仿真结果与实验结果.结论如下：

(1)优化前仿真所得最大变形量为2.172μm,优化后最大变形量为1.819μm,均发生在硅片中心部位,优化后最大变形量减小.

(2)优化前传感器输出数据与理论值之差最大为0.195V,优化后传感器输出数据与理论值之差较优化前小,最大为0.163V；优化后绝对误差最大为0.60%,比优化前的0.95%小,且优化后绝对误差曲线均在优化前绝对误差下方,说明优化后的输出数据更加接近于理论值.由此可见，基座结构的优化对于提高传感器输出性能有实际意义.

参考文献：

[1]Tanner D M.MEMS reliability:where are we now? [J].Microelectronics Reliability,2009,49(9/10/11):937-940.

[2]Ranjit Singh,Low Lee Ngo,Ho Soon Seng,et al.A silicon piezoresistive pressure sensor [C]∥Proceedings of the First IEEE International Workshop on Electronic Design,Test and Applications.Los Alamitos:IEEE Computer Society,2002:1-4.

[3]Bakhoum E G,Cheng M H M.Capacitive pressure sensor with very large dynamic range [J].IEEE Transactions on Components and Packaging Technology,2010,33(1):79-83.

[4]Ferreira C,Grinde C,Morais R,et al.Optimized design of a piezoresistive pressure sensor with measurement span of 1MPa [J].Procedia Engineering,2012,47:1307-1310.

[5]Tsouti V,Bikakis G,Chatzandroulis S,et al.Impact of structural parameters on the performance of silicon micromachined capacitive pressure sensors [J].Sensors and Actuators A,2007,137(1):20-24.

[6]Chou Tsung-lin,Chu Chen-hung,Lin Chun-te,et al.Sensitivity analysis of packaging effect of silicon-based piezoresistive pressure sensor [J].Sensors and Actuators A:Physical,2009,152(1):29-38

[7]沈艳婷,蔡绯，张洪军.静压对金属电容式差压变送器测量精度的影响 [J].传感器与微系统,2012,31(11):61-66.

Shen Yan-ting，Cai Fei，Zhang Hong-jun.Effect of static pressure on measurement precision of metal capacitive differential pressure transmitter [J].Transducer and Micro-system Technologies,2012,31(11):61-66.

[8]赵艳平,丁建宁,杨继昌,等.微型高温压力传感器芯片设计分析与优化 [J].传感技术学报,2006,19(5):1829-1831.

Zhao Yan-ping,Ding Jian-ning,Yang Ji-chang,et al.The analyses and optimization of micro-type high temperature pressure sensor chip [J].Chinese Journal of Sensors and Actuators,2006,19(5):1829-1831.

[9]Yang G,Xie H Y.Mechanical derivation of the longitudinal and transverse piezoresistive coefficient on piezoresistive pressure sensor [J].Procedia Engineering,2012,29:1612-1617.

[10]Timoshenko S P,Woinowsky-Krieger S.Theory of plates and shells[M].2nd ed.New York:McGraw-Hill,1959:51-58,391-393.

[11]Lou L,Zhang S,Park W T,et al.Optimization of NEMS pressure sensors with a multilayered diaphragm using silicon nanowires as piezoresistive sensing elements [J].Journal of Micromechanical and Microengineering,2012,22 (5):055012/1-15.

[12]许德华,祝冰.压力传感器半导体薄膜电桥优化设计 [J].传感器技术,1995 (6):20-23.

Xu De-hua,Zhu Bing.The selective design of thin semiconductors films bridge for pressure sensors [J].Journal of Transducer Technology,1995 (6):20-23.

[13]MEMS and Nanotechnology Exchange(Mnx).MEMSnet[DB/OL].www.memsnet.org/material.

[14]Rudolf Krondorfer,Yeong K Kim,Jaeok Kim,et al.Finite element simulation of package stress in transfer molded MEMS pressure sensors [J].Micro-electronics Reliability,2004,44(12):1995-2002.

[15]Linlin Z,Chen X,Shen G.Analysis for load limitation of square-shaped silicon diaphragms [J].Solid-State Electronics,2006,50(9/10):1579-1583.

Output Performance of Silicon Pressure Sensor Influenced by

Deformation of Sensor Substrate

HuGuo-qing1GongXiao-shan1ZhouYong-hong2ZouChong2JahangirAlam1

(1. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China;

2. Fujian Wide Plus Precision Instruments Co., Ltd., Fuzhou 350015, Fujian, China)

Abstract:In order to analyze the performance of silicon pressure sensor influenced by the deformation of sensor substrate, firstly, the stress distribution of pressure sensor quadrate in the thin diaphragm was deduced on the basis of elastic mechanics theory and plate-shell theory, which provided a basis for the arrangement of resisters in strain membrane. Secondly, the effect of substrate deformation on the stress difference of strain membrane was analyzed via a simulation in ANSYS environment. Then, in order to diminish the influence of sensor substrate deformation, an appropriate optimization of substrate structure was conducted, and a comparison of simulation results was made. Finally, experiments were carried out to test the outputs of the sensor before and after optimization. It is indicated that, after the optimization, the largest deformation of sensor chip center reduces from 2.172μm to 1.819μm, and the output error decreases from 0.95% to 0.60%.

Key words: pressure sensors; silicon sensors; output performance; finite element analysis; structural optimization

Foundation item: Supported by the National Natural Science Foundation of China(NSFC)(51175184)