基于边界层的一类不确定系统的迭代学习控制

基于边界层的一类不确定系统的迭代学习控制*

李向阳田森平

(华南理工大学 自动化科学与工程学院, 广东 广州 510640)

摘要：针对一类具有任意初态和非周期有界扰动的不确定非线性时变系统,提出一种基于边界层的迭代学习控制方法,将边界层设计成一个具有剩余宽度的指数衰减函数,通过边界层把任意初态问题转换为零初值迭代学习问题.针对周期和非周期不确定性扰动,分别设计周期项的学习律和非周期项的边界学习律,然后在此基础上给出了迭代学习控制算法.文中给出了相关定理,并应用类Lyapunov方法给出了定理的详细证明.仿真结果表明,所提出的算法是有效的,轨迹跟踪误差能收敛到边界层.

关键词：不确定系统；迭代学习控制;初始状态问题;边界层;类Lyapunov方法

中图分类号：TP273

doi：10.3969/j.issn.1000-565X.2015.03.016

文章编号：1000-565X(2015)03-0111-10

收稿日期：2014-09-29

基金项目：* 国家自然科学基金资助项目(61403142); 教育部博士点基金资助项目(20120172110026); 华南理工大学中央高校基本科研业务专项资金资助项目-博士启动项目(2014ZB0028)

作者简介：黄道平(1961-),男,博士,教授,主要从事故障诊断、软测量研究.E-mail: audhuang@scut.edu.cn

在迭代学习控制(ILC)的研究中,往往要求每次迭代的系统初始状态和期望轨迹的初值一致[1],但是在实际应用时,每次迭代学习不可避免地存在初始误差,迭代学习控制的初始值问题是迭代学习控制研究的基本问题.解决初始值问题的方法有初始控制量校正和初始期望轨迹校正等.初始控制量校正方法又可分为压缩映射方法[2-6]和类Lyapunov方法[7-8].初始期望轨迹校正的方法是在较小的初始时间区间上设计一段从零初始值到期望轨迹的过渡轨迹[4,9],过渡轨迹之后采用原来的期望轨迹.近年来,基于边界层的初值问题解决方法也得到关注[10-11],基于边界层的方法能兼顾跟踪误差的控制精度和初始过渡过程的控制量大小,方便实际应用.

实际的被控对象往往是非线性时变的,除了有周期不确定项外,还有非周期扰动.对于周期不确定项,如果它满足线性参数化条件,即不确定项可分解为一个与状态无关的未知时变函数和一个与状态有关的已知时变函数的乘积的形式,则可以应用自适应迭代学习方法来求解[9,12-17].如果周期不确定项不满足线性参数化条件,则不能直接应用上述自适应迭代学习控制方法来求解,文献[18]应用模糊系统建模的方法把系统不确定项建模为满足上述线性参数化形式,再采用自适应迭代学习控制方法求解,同时建模误差采用鲁棒控制的方法来克服.对于系统不确定项不满足线性参数化条件的迭代学习控制问题,文中提出一种直接对系统不确定项进行学习的迭代学习控制算法；另一方面,对于非周期扰动,一般扰动的界是有限的[18],根据该特点,提出了一种适合对非周期扰动的界进行学习的迭代学习控制方法.

1问题的提出

考虑如下2-D形式表示的不确定非线性时变系统的迭代学习控制:

⋮

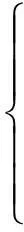
(1)

假设1期望轨迹r1(t)在工作区间t∈[0,T]有n阶导数,且有

(2)

假设2f和b在r的邻域D(r∈D⊂Rn)上有界且满足局部Lipschitz连续条件,且b的符号保持不变.设x1、x2和x为D中系统任意状态,则有：

(3)

(4)

(5)

(6)

式中，Lf、fM、Lb、bm和bM为适当正数.

假设3d为任意非周期有界扰动,有

(7)

式中dM(t)为扰动的界.

假设4xi(0,k)为系统状态的任意初始值,即∃i∈[1,n],xi(0,k)≠ri(0),ri(0)为期望轨迹的初始值,但有x(0,k)∈D.

定义跟踪误差为

ei(t,k)=xi(t,k)-ri(t)

(8)

则系统(1)的迭代学习控制问题是一个具有非零初始误差和周期不确定性以及非周期扰动的迭代学习控制问题.

2　迭代学习控制器设计

由式(8)可以定义滑动面S(t,k)为

(9)

式中：e=(e1,e2,…,en)T，为误差向量；c=(c1,c2,…,cn)T，为Hurwitz多项式的系数向量,且取cn=1.由Hurwitz多项式的性质有,当S(t,k)有界收敛时,ei(t,k)也有界收敛.由式(9)有

(10)

对于系统(1)的迭代学习控制,有初始值扰动和任意非周期有界扰动,为此引入边界层方法来克服其扰动.

2.1　边界层设计

针对系统(1)的非零初始误差,设计如下时变边界层函数：

S(t,k)+φ(t,k),S(t,k)<-φ(t,k)

(11)

式中,S(0,k)为滑动面函数的初始值,φ(t,k)为

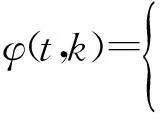
(12)

式中:α>0,为衰减因子；δ>0，为跟踪容许误差.由式(11)所定义的修正滑动面Sφ(t,k)满足零初始条件,即有

Sφ(0,k)=0

(13)

由式(11)有Sφ(t,k)的导数为

(14)

式中Iδ(S(0,k))为示性函数,定义为

(15)

在上述边界层基础上可以设计系统(1)的迭代学习控制算法.

2.2　迭代学习控制算法设计

为实现对非周期扰动d(t,k)界的限幅学习,定义如下饱和函数

(16)

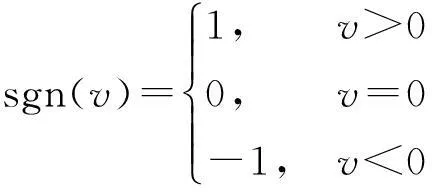
(17)

对于式(16)的饱和函数,有如下引理1.

(18)

证明分3种情况证明.

证毕.

对于系统(1)的控制增益b(t,x),实际中总是可以对其获得一个粗略的估计,可以以此为基础进行控制算法设计.

假设5系统(1)的b(t,x)有一个符号相同的估计b0(t,x),且b0(t,x)同样满足式(5)和式(6).

对式(11)边界层,设计如下限幅学习律实现对d(t,k)边界的学习:

(19)

对系统(1)中f(t,x)和b(t,x)的迭代学习,定义如下综合函数：

(20)

并设计如下学习律对其进行学习:

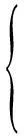
v2(t,k)=v2(t,k-1)+γ2Sφ(t,k)

(21)

式中,γ2>0，为学习增益.

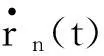
(22)

(23)

在上述式(19)和式(21)学习律基础上,设计如下控制律对系统(1)进行迭代学习控制：

(24)

式中，β≥0，为控制律的反馈增益.

2.3收敛定理及其证明

基于式(19)和式(21)的学习律和式(24)的控制律有定理1.

定理1对于系统(1)的迭代学习控制,在时间区间t∈[0,T]上进行迭代学习控制,在满足假设1-5前提下,采用式(19)和式(21)的学习律和式(24)的控制律,可以实现所要求的控制精度,即有下列结论.

(1)Sφ(t,k)有界,且有下式成立：

(25)

(2)S(t,k)有界,且有下式成立：

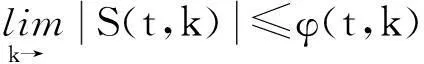
(26)

证明由式(10)和式(1)有

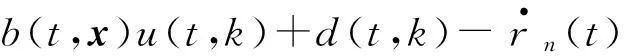
(27)

由式(14)有

(28)

结合式(27)和式(28)有

(29)

把式(24)的控制量代入式(29)并整理有

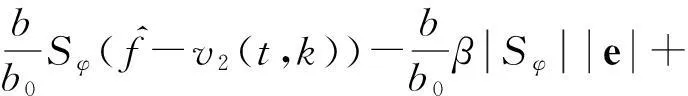
(30)

(31)

由式(12)有

(32)

考虑到式(32),由式(30)有

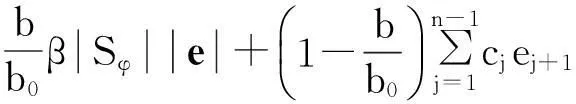
(33)

定义V(t,k)为如下类Lyapunov函数[19-21]:

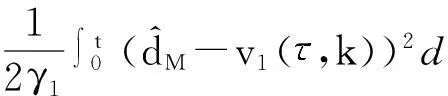
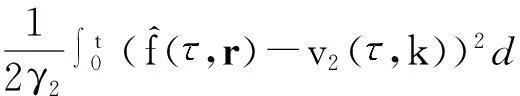
(34)

式中，

(35)

先证明ΔV(t,k)的单调性，然后证明Sφ(t,k)的收敛性.由式(33)有

ΔV(t,k)=V(t,k)-V(t,k-1)=

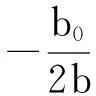
(36)

式中，

把式(33)带入Part0,并考虑零初始条件有

(37)

对Part1应用(a-q)2-(a-h)2=-(q-h)2-2(q-h)(a-q)(式中a、q、h为实数)有

由学习律式(19),上式中第2个积分的被积函数可化为

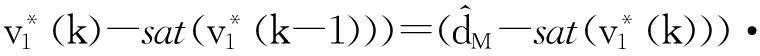
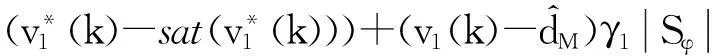
对上式应用引理1有

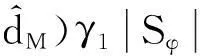
把上式代入Part1有

(38)

对Part2应用(a-q)2-(a-h)2=-(q-h)2-

2(q-h)(a-q)有

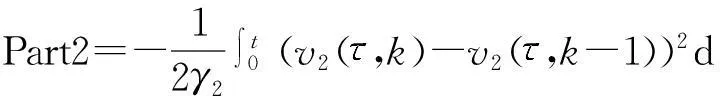
把学习律(21)代入上式Part2中有

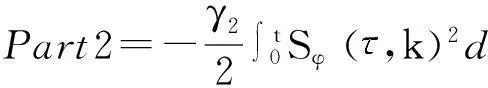
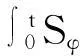
(39)

把式(37)-(39)代入式(36)有

(40)

式中，

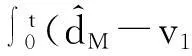
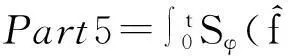
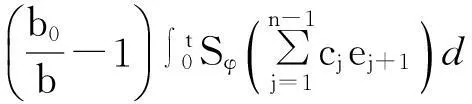
(41)

Part4可以化简为

(42)

式(41)右边取绝对值并考虑式(22)有

(43)

考虑到式(42)和式(43),由式(40)有

(44)

选取

(45)

则由式(44)有

(46)

由于b0与b具有相同的符号,因此ΔV(t,k)是随k递减的.

下面证明Sφ(t,k)的收敛性.先证明V(t,1)有界,V(t,k)第1次迭代值为

V(t,1)=ΔV(t,1)+V(t,0).

把式(36)中k=1的情况带入上式,并采用获得式(44)的推导方法可得

(47)

当满足式(45)时，由式(47)和定义式(34)有

(48)

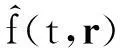
(49)

由于V(t,k)有界和收敛,则Sφ(t,k)也有界和收敛,从而e(t,k)和u(t,k)都有界和收敛.

由于

V(t,k)=(V(t,k)-V(t,k-1))+…+

(V(t,2)-V(t,1))+V(t,1),

重复应用式(46)有

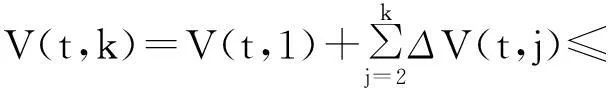
对上式两边取极限有

(50)

(51)

因此,根据式(15)有

即式(25)和式(26)成立.

证毕.

关于定理1的说明如下:

(1)随着迭代次数增加,定理1的迭代学习控制算法是把滑动面误差曲线S控制在边界层[-φ,φ]内.φ(t,k)可以采用不同的形式,选择δ>0,一方面可以避免计算过程中出现的数值不稳定,另一方面可以减少控制量的抖动.

(2)在应用定理1时,不要求像自适应迭代学习控制那样要求f(t,x)和b(t,x)满足参数化条件,而且只需通过试验数据对b(t,x)进行粗略估计,甚至可以直接根据式(6)取其边界之间的常数，如sgn(b(t,x))(bm+bM)/2，控制算法自动通过迭代学习补偿未建模部分；当b(t,x)的估计误差较大时,从式(45)可以看出,需要较大的反馈增益β才能保证时间域稳定性.

(3)从定理1的证明过程中可以看出,只要γ1>0和γ2>0即可保证迭代域的收敛性,但是较大的γ1和γ2具有较快的收敛速度.为保证周期扰动的学习速度快于非周期扰动的学习速度,实际中可以选择γ2>20γ1,这样可使控制更加光滑和节能.

3仿真研究

考虑如下的二阶非线性不确定系统[18]:

(52)

式中:

(53)

(54)

d(t,k)=d1sinω1+d2cosω2

(55)

其中，d1=rand,d2=rand，ω1=5rand,ω2=5rand.

式(52)-(55)中，x1(t,k)和x2(t,k)分别为倒立摆的角位移和角速度,g为重力加速度,mc为小车的质量,m为摆的质量,l为摆的半长度,u为摆的作用力.采用与文献[18]相同的参数进行仿真,取mc=1,m=0.1，l=1,rand为输出为0～1之间的随机函数.期望轨迹为

(56)

系统状态初值为

(57)

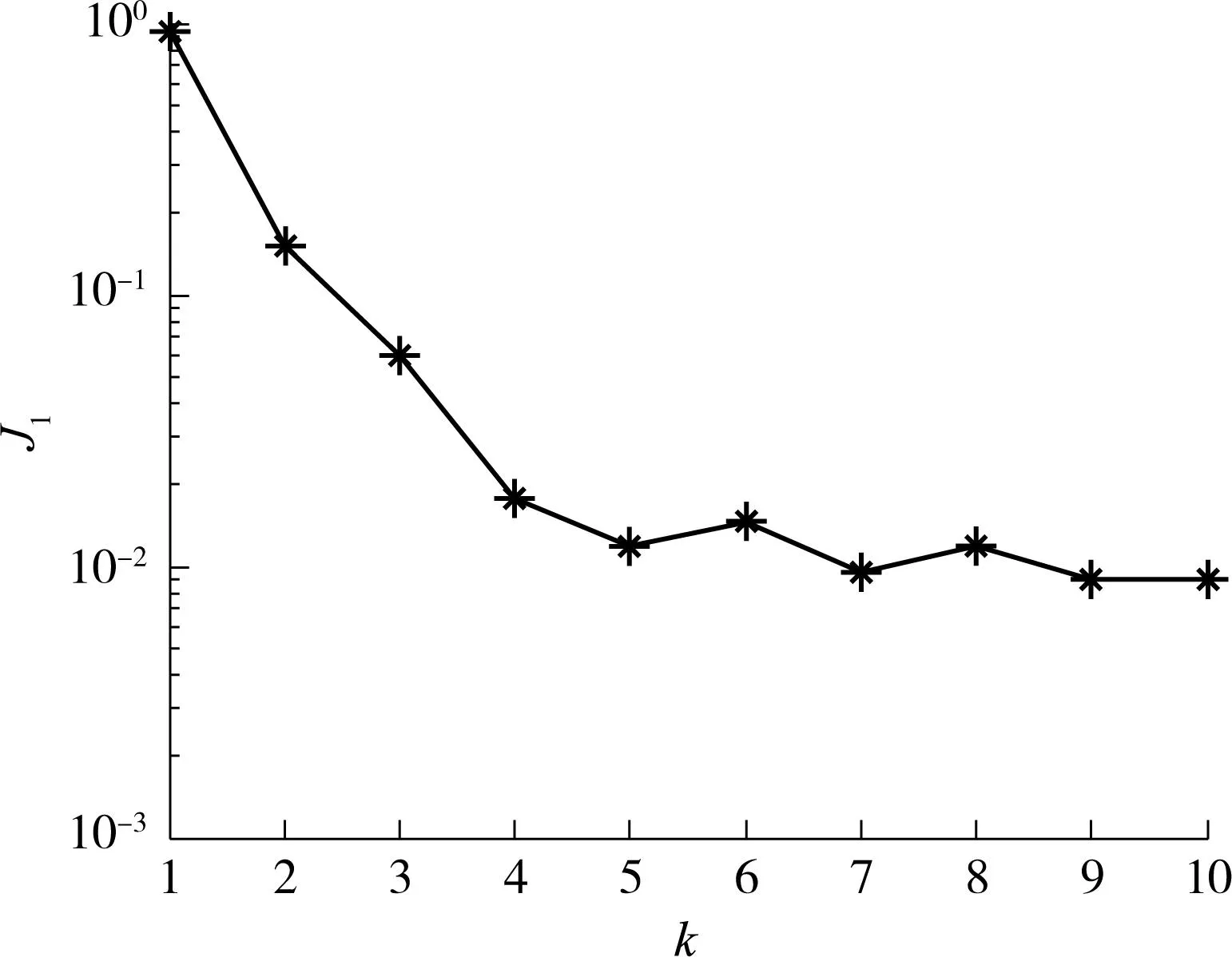
图1　J 1随迭代次数k的变化规律 Fig.1　J 1 versus iterations k

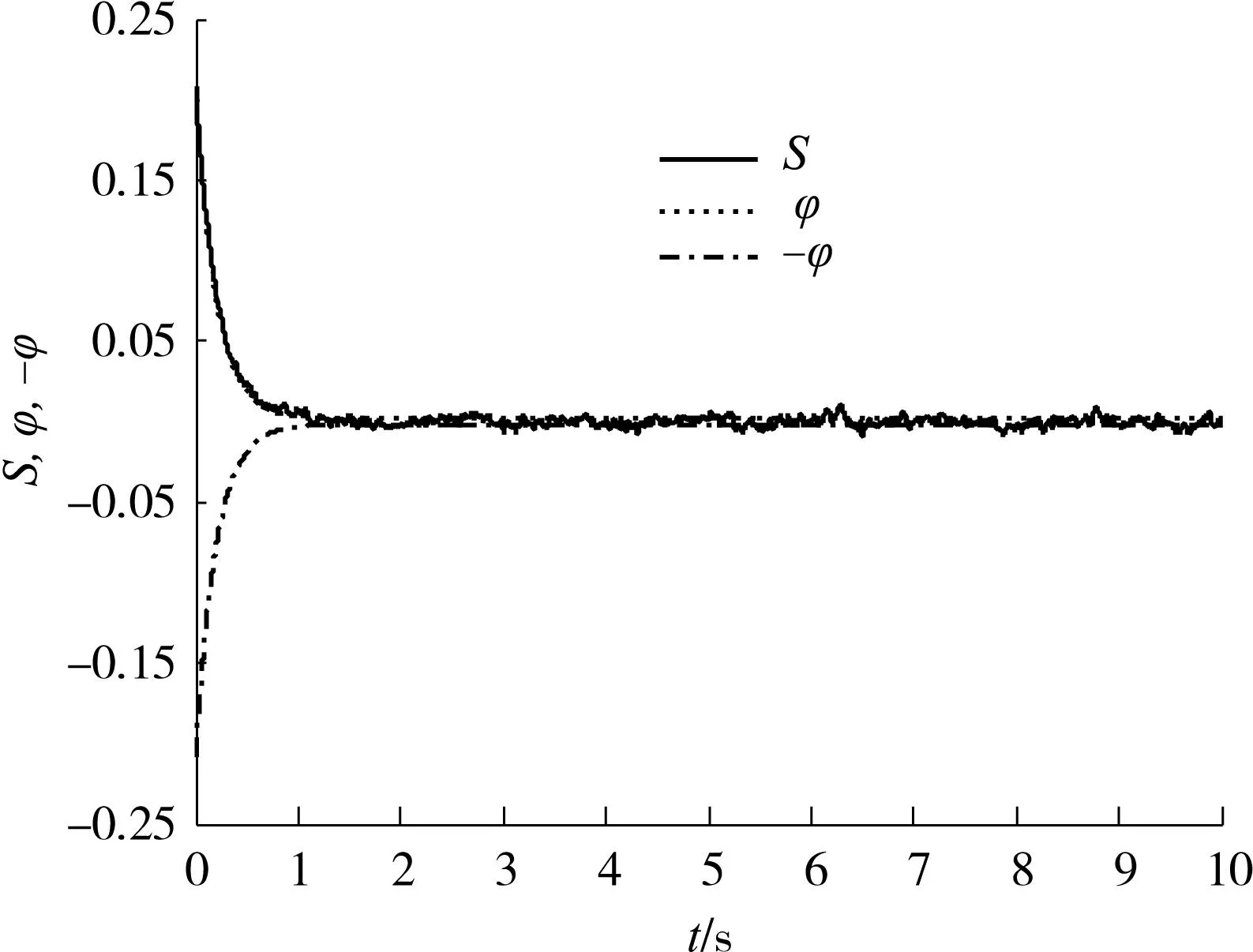
图2　S(t,k)与φ(t,k)随时间的变化规律 Fig.2　S(t,k) and φ(t,k) versus time

图3　第10次迭代后的r 1和x 1 Fig.3　r 1 and x 1 at the 10th iteration

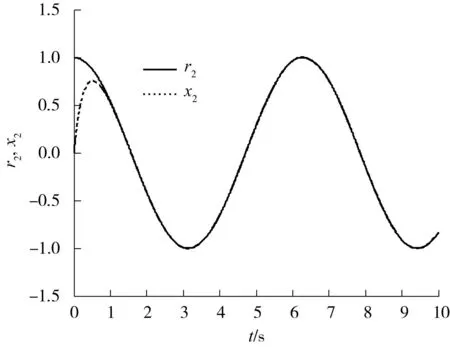
图4 　第10次迭代后的r 2和x 2 Fig.4　r 2and x 2 at the 10th iteration

图5　第10次迭代后的控制输入u Fig.5　Control input u at the 10th iteration

仿真结果表明,随着迭代次数的增加,系统轨迹的跟踪误差迅速减少,经过10次迭代后的滑动误差完全在边界层以内,得到了满意的效果.对比文献[18]的图1可以看出,文中方法具有更快的收敛速度.

4结语

文中提出了一种适合任意初始条件和任意有界干扰的基于边界层的不确定系统的迭代学习控制方法,给出了相关算法定理,并应用类Lyapunov方法给出了详细证明,该算法不要求系统的不确定项满足线性参数化条件,只需了解不确定部分的粗略估计和变化范围,估计误差通过迭代学习自动补偿.仿真结果表明，文中提出的算法是有效的,比要求系统不确定项满足线性参数化条件的自适应迭代学习控制方法具有更好的适用性.

参考文献：

[1]TianSen-ping,XieSheng-li,FuYu-li.Fastalgorithmofiterativelearningcontrol[J].JournalofSouthChinaUniversityofTechnology:NaturalScienceEdition,2002,30(5):37-40.

田森平，谢胜利，傅予力.一种新的迭代学习控制快速算法[J].华南理工大学学报：自然科学版，2002,30(5):37-40.

[2]PorterB,MohamedSS.Iterativelearningcontrolofpartiallyirregularmultivariableplantswithinitialimpulsiveaction[J].InternationalJournalofSystemsScience,1991,22(3):447-454.

[3]LeeHS,BienZ.Studyonrobustnessofiterativelearningcontrolwithnon-zeroinitialerror[J].InternationalJournalofControl,1996,64(3):345-359.

[4]孙明轩,黄宝健.迭代学习控制[M].北京:国防工业出版社,1999.

[5]ParkKH.Anaverageoperator-basedPD-typeiterativelearningcontrolforvariableintialstateerror[J].IEEETransactionsonAutomaticControl,2005,50(6):865-869.

[6]阮小娥,赵建永.具有初始状态不确定性的非线性系统脉冲补偿迭代学习控制[J].控制理论与应用,2012,29(8):993-1000.

RuanXiao-e,ZhaoJian-yong.Pulsecompensatediterativelearningcontroltononlinearsystemswithinitialstateuncertainty[J],ControlTheory&Applications,2012,29(8):993-1000.

[7]SunMing-xuan,WangDan-wei.Iterativelearningcontrolwithinitialrectifyingaction[J],Automatica,2002,38(7):1177-1182.

[8]LiXD,ChowTWS,HoJKL,etal.Iterativelearningcontrolwithinitialrectifyingactionfornonlinearcontinuoussystems[J].IETControlTheoryandApplicaition,2009,3(1):49-55.

[9]孙明轩,严求真.迭代学习控制系统的误差跟踪设计方法[J]．自动化学报，2013,39(3):251-262．

SunMing-xuan,YanQiu-zhen.Errortrackingofiterativelearningcontrolsystems[J].ActaAutomaticaSinica,2013,39(3):251-262.

[10]ChienChiang-ju,HsuChun-te,YaoChia-yu.Fuzzysystem-basedadaptiveiterativelearningcontrolfornonli-nearplantswithinitialstateerrors[J].IEEETransactionsonFuzzySystems,2004,12(5):724-732.

[11]何熊熊,秦贞华,张端.基于边界层的不确定机器人自适应迭代学习控制[J]．控制理论与应用，2012,29(8):1090-1093．

HeXiong-xiong,QinZhen-hua,ZhangDuan.Adaptiveiterativelearningcontrolforuncertainrobotbasedonboundarylayer[J].ContorlTheory&Applications,2012,29(8):1090-1093.

[12]YinChenkun,XuJian-xin,HouZhongsheng.AnILCschemeforaclassofnonlinearsystemswithtime-varyingparameterssubjecttosecond-orderinternalmodel[C]∥ProceedingsofJoint48thIEEEConferenceonDecisionandControland28thChineseControlConference.Shanghai:IEEE,2009:452-457.

[13]YinChenkun,XuJian-xin,HouZhongsheng.Ahigh-orderinternalmodelbasediterativelearningcontrolfornonlinearsystemswithtime-iteration-varyingparameters[J].IEEETransactionsonAutomaticControl,2010,55(11):2665-2670.

[14]朱胜，孙明轩，何熊熊．严格反馈非线性时变系统的迭代学习控制[J]．自动化学报，2010,36(3):454-458．

ZhuSheng,SunMing-Xuan,HeXiong-Xiong.Iterativelearningcontrolofstrict-feedbacknonlineartime-varyingsystems[J].ActaAutomaticaSinica,2010,36(3):454-458.

[15]XuJX,YanR.Oninitialconditionsiniterativelearningcontrol[J].IEEETransactionsonAutomaticControl,2005,50(9):1349-1354

[16]ParkBH,KuntY,LeeJS.Adaptivelearningcontrolofuncertainroboticsystems[J].InternationalJournalofControl,1996,65(5):725-744.

[17]XuJian-xin.Recentadvancesiniterativelearningcontrol[J].ActaAutomaticaSinica,2005,31(1):132-142.

[18]ChienChiang-ju.Acombinedadaptivelawforfuzzyite-rativelearningcontrolofnonlinearsystemswithvaryingcontroltasks[J].IEEETransactionsonFuzzySystems,2008,16(1):40-51.

[19]XuJian-xin,XuJing.Oniterativelearningfromdifferenttrackingtasksinthepresenceoftime-varyinguncertainties[J].IEEETransactionsonSystems,Man,andCybernetics-PartB:Cybernetics,2004,34(1):589-597.

[20]ChiRonghu,HouZhongsheng,XuJianxin.AdaptiveILCforaclassofdiscrete-timesystemswithiteration-varyingtrajectoryandrandominitialcondition[J].Automatica,2008,44(8):2207-2213.

[21]XuJian-xin,YingTan.Acompositeenergyfunction-basedlearningcontrolapproachfornonlinearsystemswithtime-varyingparametricuncertainties[J].IEEETransactionsonAutomaticControl,2002,47(11):1940-1945.

BoundaryLayer-BasedIterativeLearningControlforaClassof

UncertainSystems

Li Xiang-yangTian Sen-ping

(SchoolofAutomationScienceandEngineering,SouthChinaUniversityofTechnology,Guangzhou510640,Guangdong,China)

Abstract:For a class of uncertain nonlinear time-varying systems with arbitrary initial states and aperiodic bounded disturbance, an iterative learning control (ILC) method on the basis of boundary layer is presented. In this me-thod, boundary layer is designed as a decaying exponential function with residual width, the arbitrary initial state problem of ILC is transformed into a zero initial state problem by the designed boundary layer, and learning laws of periodic and aperiodic terms are designed for periodic and aperiodic disturbances, respectively. On the basis of these two laws, an ILC algorithm is presented, and the corresponding theorem is given with detail proof through Lyapunov-like approach. Simulated results show that the proposed algorithm is effective and is capable of converging trajectory tracking errors to boundary layer.

Keywords:uncertainsystem;iterativelearningcontrol;initialstateproblem;boundarylayer;Lyapunov-likeapproach

Foundationitems:SupportedbytheNationalNaturalScienceFoundationofChina(NSFC) (61403142)andthePh.D.ProgramsFoundationofMinistryofEducationofChina(20120172110026)

†通信作者： 邱禹(1988-),男,博士生,主要从事故障诊断研究.E-mail:qy-zq1988@163.com