基于灵活LBP纹理字典构造及多特征描述的改进SCSR算法

基于灵活LBP纹理字典构造及多特征描述的改进SCSR算法*

马丽红黄茵黎剑晖

(华南理工大学 电子与信息学院//国家移动超声探测工程技术研究中心， 广东 广州 510640)

摘要：针对超分辨率重构字典对结构区分度不够、在最优匹配原子搜索中耗时太长的问题,提出了一种多特征联合的分级字典(MFJD).首先,分别用边缘块梯度特征和纹理块局部二值模式(LBP)特征来构建两种分类字典,用于逼近不同类型结构；其次,采用树结构来聚类原子,实现同一字典下的快速原子匹配；最后,引入双边总变分(BTV)正则项来约束重构结果.实验表明：与经典稀疏编码超分辨率重构(SCSR)算法相比,MFJD多特征联合的分级字典使重构图像的PSNR值提高了0.2424dB,使平均结构相似度(MSSIM)和特征相似度(FSIM)分别提高了0.0043和0.0056；由于结构分类字典维数降低,重构时间降至SCSR算法的22.77%.

关键词：超分辨率重构；结构分类；多特征描述；LBP纹理；双边总变分

中图分类号：TP391

doi：10.3969/j.issn.1000-565X.2015.03.009

文章编号：1000-565X(2015)03-0066-06

收稿日期：2014-06-06

基金项目：* 工业控制技术国家重点实验室开放课题(ICT1434)；广东省自然科学基金博士启动项目(S2013040014995)；华南理工大学中央高校基本科研业务费资助项目(2014ZM0044)

作者简介：赵俊红(1976-)，女，讲师，博士，主要从事图像取证、图像分析与理解研究.E-mail: jhzhao@scut.edu.cn

超分辨率(SR)重构技术通过对低分辨率(LR)成像估计丢失的信息来获得高分辨率(HR)信号,它对城市交通和安防监控、郊外环境及军事目标监测、生物医学影像处理意义重大.其中学习型单帧SR重构算法最大限度地利用了空域结构先验信息,利用典型HR图像训练块与其对应LR块之间的映射,通过单帧重构完成对细节信息的学习和计算补偿,它成功的关键在于构造准确的映射模型.

根据信号结构描述方式,单帧模型分3类:①基于上下文保真和迭代投影逼近的学习,包括马尔科夫场模型(MRF)[1]、凸集投影(POCS)[2]和迭代反投影(IBP)[3]等算法；②基于拓扑结构保持的信号流形描述,代表性算法有局部线性嵌入算法(LLE)[4-5]；③基于结构分解的模型,其中稀疏编码类超分辨率重构(SCSR)[6-7]因避免了上下文相关和迭代投影的庞大HR/LR 数据库,并克服了流形学习易产生的欠拟合或过拟合现象,成为近年SR研究的热点.

不同分辨率的同一区域信号特征相同,SCSR算法用稀疏字典和稀疏系数来关联LR、HR块；重构时LR块首先通过字典稀疏系数确定HR映射块,再用特征符号搜索算法(FSS)求解l1约束优化问题[8],其改进方法有:①通过构造几何字典,改善算法的边缘保持能力[9].几何字典的构造原理是依靠奇异值分解(SVD)来计算各块边缘主方向的梯度角,再用K-SVD算法求解稀疏系数，同时引入非局部相似度约束,较准确地恢复了简单的直线边缘.②考虑到人眼对图像显著内容的敏感性,引入一个显著图字典[10].首先,分割显著图用于提取感兴趣区域；其次,显著区域的块稀疏系数与其8个相邻块稀疏系数的线性加权,用于去除显著区域的边界效应；附加的显著图字典提高了字典训练的速度,但对非梯度突变结构效果受限.

用结构分解和稀疏系数来高效地表示图像细节,SCSR算法面对的困难是:①单个梯度特征虽然简单,但仅靠梯度算子来描述,与多结构并存、多特征描述的信号本质不符,导致重构时的原子稠密加权问题,这对纹理结构尤其明显；②单一字典维数过大,造成匹配原子的搜索和计算代价过高.为此,文中建立了多特征联合的分级字典(MFJD).

1联合稀疏编码算法的原理和局限性

对于希尔伯特空间的一个过完备字典D∈Rd×K(d≤K),若任意信号x可由D的K个d维向量的少量原子线性组合逼近,则x可被D稀疏编码[11]:

x≈Dα0

(1)

式中:稀疏向量α0∈RK,由少数非零值组成；ε为约束阈值.

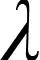
(2)

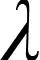
(3)

式中,

(4)

1.1梯度算子描述的局限性

对信号结构的描述方式,由特征算子F产生的字典原子决定.人眼对图像高频信息敏感,因此一阶和二阶梯度作为低复杂度高频特征的简单描述,成为SCSR算法特征算子首选:

(5)

(6)

式中,f1、f3为提取水平梯度特征,f2、f4为提取垂直梯度特征.梯度值大小反映了边缘强弱,适合描述梯度值大的图像边缘；但结构较复杂的信号,如纹理图像,其梯度值变化程度小于阶跃边缘,重构时选入的加权原子数目较多,重构纹理趋于平滑,细节丢失.取5幅均含有大量阶跃边缘及纹理信号的标准测试图像(Airplane、Man、Lena、Rough及Grass),共有1.617×106个图像块,其中平滑块、边缘块及纹理块分别占47.3%、27.1%及25.6%,利用SCSR重构时,单一梯度特征字典对边缘块重构的平均PSNR值比纹理块的大0.2982～0.5314 dB,可见梯度特征算子描述纹理信号的能力有限；而这5幅图像重构选入的加权原子数目为1.794×106至4.690×106,纹理信号分解的非稀疏性明显.

18718919219719519019619719919319319719919215819919918914910820018213010098

186192197198195192196199194181200202195178150199192174152125189167134114106

(a)原始HR图像块 (b)LR图像块

图1HR与相应LR图像块灰度值

Fig.1Gray values of an HR block and its LR one

1.2最优原子搜索的代价和描述误差

因为下采样信息丢失,从LR到HR的估计,是不适定的一对多映射关系,是信号的估计过程[12].若X为复原HR块,Y为输入LR块,B和S分别为系统退化和下采样算子,则全局SR优化模型[6]为

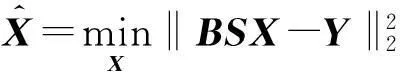
(7)

Yi=BSXi-1

(8)

相对LR信号Y,每次迭代的Yi残差信息ei需补偿到下一轮迭代获得的HR图像中.因为残差ei为

ei=Y-Yi=Y-BSXi-1

(9)

ei的插值结果ei′就是上一轮估计值Xi-1的HR残差,因此可计得第i次估计值Xi:

Xi=Xi-1+ei′

(10)

迭代式(8)至(10),ei中元素均值收敛于ζ,A(en)≤ζ时得最优解Xi，其中A(·)为向量元素均值.

用FSS算法对字典D∈Rd×K用式(4)求块稀疏系数,含Kd次乘法及d次求和,复杂度为O(Kd)；设稀疏度为Σ,用式(1)猜测特征符号需KΣ次乘及Σ次加操作,复杂度O(KΣ).因此,求解每块的总复杂度为O(Kd)+O(KΣ).同时,残差ei插值为ei′,假设信号具有连续性,与梯度算子反映差异的本质相反,用插值方式逼近HR残差并逐次叠加到HR复原图像中,会造成较大的误差积累和边缘振铃效应.

2局部二值模式特征算子和纹理字典基原子

为提高单个原子的结构表示能力,不同内容应采用不同特征描述.平滑块用经典插值算法更快速,一、二阶梯度滤波器适合描述阶跃边缘,而大部分纹理信号虽然具有准周期性,却不是适合梯度描述的序率信号,基于梯度的纹理信号分解有大量长拖尾的小值数据,难以保证稀疏性.局部二值模式(LBP)[13]是近年被广为接受的纹理特征,文中基于LBP矢量来构建纹理字典.

2.1LBP特征矢量与字典原子映射

LBP局部纹理描述算子,通过对中心像素与邻域像素的灰度差进行编码来描述纹理,具有旋转不变性和灰度不变性.在3×3窗模板中,比较模板中8个非中心位置的灰度值和中心位置的灰度值的大小,产生8个0、1组成的局部二进制模式值LBP:

(11)

(12)

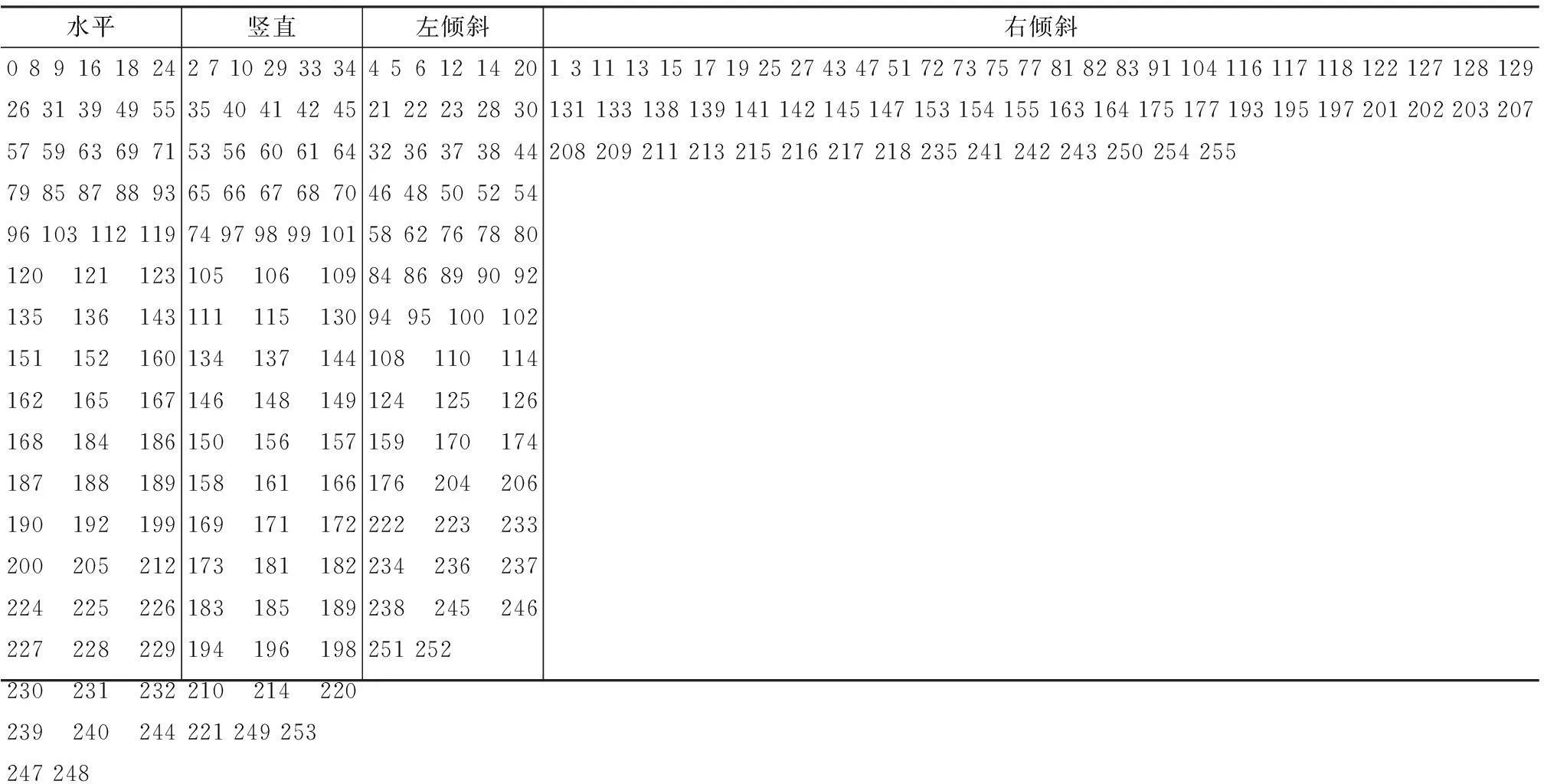
式中，ωj是第j个像素的编码,Ij是非中心位置第j个像素值,I0是中心像素值.图2(a)中LBP=00010000,对应十进制数16,共有256种不同LBP特征.按纹理方向分为水平、竖直、左倾斜和右倾斜情况 (见图2(b)-(e)),表1给出了4种纹理方向的详细LBP码字.

(a)示例(b)水平 (c)竖直(d)左倾斜(e)右倾斜

图2LBP值示例及4方向纹理分组

Fig.2LBP demo and dominant directions of four texture groups

表1 各方向纹理组的LBP编码列表(十进制)
Table 1Decimal LBP codewords grouped by texture directions

水平竖直左倾斜右倾斜0891618242631394955575963697179858788939610311211912012112313513614315115216016216516716818418618718818919019219920020521222422522622722822923023123223924024424724827102933343540414245535660616465666768707497989910110510610911111513013413714414614814915015615715816116616917117217318118218318518919419619821021422022124925345612142021222328303236373844464850525458627678808486899092949510010210811011412412512615917017417620420622222323323423623723824524625125213111315171925274347517273757781828391104116117118122127128129131133138139141142145147153154155163164175177193195197201202203207208209211213215216217218235241242243250254255

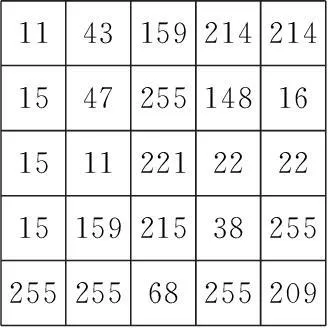
图3为f1梯度特征与LBP特征描述纹理块的结果,图3 (a)、(b)为原始图及其灰度值.图3(c)梯度特征为小值,差异小,纹理块突变与缓变区分不明显,在图3(d)的LBP特征中差异更明显.

1361141071101181141069811313710610310210712597921021061029191106102104

(a)原始图像块(b)图3(a)的灰度值

22294-11-8816-7-39-2434-4-23-185-5-14040-15-112-2

114315921421415472551481615112212222151592153825525525568255209

(c)f1梯度特征(d)LBP描述

图3纹理块的不同特征描述

Fig.3Different feature descriptions of a texture block

2.2双边总变分约束

从LR图像重构HR图像是病态求解,需要合适的正则约束项.正则项选取原则有两个:①提高信号保真度,尽可能恢复图像细节信息；②抑制噪声的同时,防止图像边缘被平滑.双边总变分(BTV)正则项[14-15]通过双边滤波器和移位算子来保全邻域关系和有效边缘,采用总变分(TV)最小化寻优.

文中采用的BTV正则项是

(13)

(14)

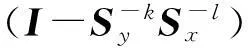
(15)

2.3原子图样的尺度伸缩和误差增量补偿

为减少HR-LR图像映射前后的动态范围改变,抑制边缘、纹理结构的平滑趋势,对训练集进行高频预提升,训练图像中的点(r,s)经过双三次插值伸缩后,其灰度值为

(16)

式中,aij为依赖于插值数据的特性,g(·)为控制高频增强的效果,叠加在aij上预提升原始像素值高频成分.

图4是高频预提升后HR及其相应的LR图像块,其标准差分别为66及52.与未作预提升的图1相比(标准差分别为33和29),结构差异性增大.因为式(16)中g(aij)预提升了高频成分,降低了插值系数aij的影响程度,所以在保留更多高频信息的基础上,动态范围的误差比重降低,突出了图像结构的差异性,使边缘、纹理结构在尺寸伸缩中不易被平滑化.

13914816117918015517618519618817319020319311520020919210062161806000

1361561741831831601761881821571891981921579419818715510949186142763520

(a)原始HR图像块(b)LR图像块

图4高频预提升后HR、LR块灰度值

Fig.4Gray values of HR and LR blocks after high frequency boost

3多特征字典分级树结构及训练重构

多特征联合的分级字典MFJD采用不同特征算子,根据不同图像块内容来构造联合的分级字典,可以有效实现字典降维和结构准确匹配.图5给出了分级树结构,在梯度字典中的树结构分为一阶及二阶梯度特征子字典,纹理字典的方向树结构分为水平、竖直、左倾斜及右倾斜方向子字典.

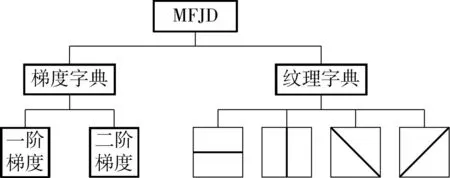
图5　多特征分类字典及其分级树结构 Fig.5　Multi-feature joint dictionaries and their classification trees

MFJD算法在字典训练时依据图像熵E及方差σ2对图像块分类,图像熵E定义为

(17)

式中，L是灰度级数,pj是第j个像素灰度概率.方差σ2为

(18)

式中,qj是第j个像素灰度值,μ是块平均灰度值.基于平滑/边缘/纹理块可接受分类错误率准则,设置图像熵阈值H1区分平滑块,再比较方差阈值H2区分边缘和纹理块.因此图像块分类准则为:

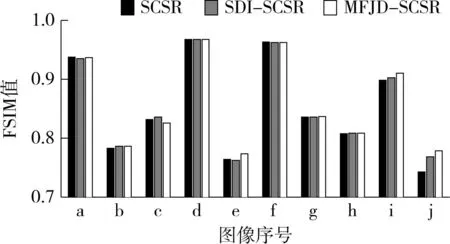
(1)当E

(2)当E>H1且σ2>H2时,该图像块判为边缘块；

(3)当E>H1且σ2

平滑、边缘及纹理块将组合起来迭代训练边缘结构字典Dhe、Dle和纹理结构字典Dht、Dlt，原理是：根据式(2),首先固定Dhe、Dle或Dht、Dlt,求解当前最优稀疏系数Z；然后保持Z不变,更新字典Dhe、Dle或Dht、Dlt；重复至字典收敛.训练步骤如下:

(1)按方差σ2和熵E,图像块分为平滑/边缘/纹理块；

(2)提取不同块特征，边缘块用式(6)的梯度算子描述,纹理块采用式(12)的LBP描述；

(3)根据式(2)联合稀疏编码字典训练方法,迭代更新得到边缘字典Dhe、Dle和纹理字典Dht、Dlt.

输入LR信号则按以下步骤实现SR字典重构:

(1)用双三次插值算法将输入LR图像重构至所需尺寸,然后分块并分类,平滑块直接视作HR平滑块；

(2)对边缘块提取梯度特征,对纹理块提取LBP码；

(3)按式(4)计算块稀疏系数,用相应字典重构HR块；

(4)按式(15)BTV正则项函数,迭代求解HR图像.

4实验结果与分析

用峰值信噪比(PSNR)、结构相似度 (MSSIM)和特征相似度(FSIM)作为重构质量的评价指标.设X1为M×N原始HR图像,X2为重构HR图像,PSNR为

(19)

PSNR单位为dB.另外从感知角度衡量,MSSIM为

(20)

(a)Airplane,

512×512(b)Man,

256×256

(c)Face,

276×276(d)Flower,

512×480

(e)Leaves,

256×256(f)Lena,

512×512

(g)Rough,

512×512(h)Grass,

512×512

(i)Word,

256×256(j)Line,

256×256

图6标准SR算法测试图像

Fig.6Standard test images for SR algorithms

式中,bi、ci、hi分别是X1和X2的第i个图像块的亮度、对比度及结构比较函数,α、ρ、γ是三者的调整权值,W是图像块的数目.类似地,FSIM为

(21)

式中,SL(X1,X2)、G(X1,X2)分别是相位一致性特征和梯度特征的相似度测量,PSNR、MSSIM及FSIM值越大,重构图像的特征与原始图像的特征相接近,重构质量越好.

4.1字典维数的选取分析

字典维数越大,原子数(直接逼近的结构)越多,重构质量越好；但训练和匹配耗时越长,需要平衡训练/重构时间和重构质量.观察单字典维数为64、128、256、512和1024时的训练时间曲线 (见图7,×2表示梯度和纹理双字典),可见:①字典维数和训练时间呈指数式单增关系；②当维数为256和512时,训练时间增幅较小,256/512维字典是合适的.

图7　字典维数与训练时间关系 Fig.7　 Relationship between dictionary sizes and training time

图8是同一图像在不同维数字典下的重构结果,对局部放大的花瓣检测结构和色彩失真,高维重构图8(d)、(e)比低维图8(a)-(c)明显清晰,后者存在明显的边缘赘生伪影.此时512维字典更合适.

(a)64×2

(b)128×2(c)256×2

(d)512×2(e)1024×2

图8 不同字典维数下重构结果

Fig.8 Reconstructed results by dictionaries with different sizes

表2、表3对比了不同维数字典的重构结果和时间.从表2知:①重构PSNR值随维数增大而提高；②当维数为512时,重构质量的升幅最优,提高了0.0687dB.从表3看,由于重构需要大量搜索最匹配原子,所以随维数增加,重构时间变长.综合三者情况,当单字典维数为1024时,其重构时间增幅近1min,而PSNR值的提升仅有0.0278 dB,比512维字典低效,因此确定选择单个字典维数为512.

表2不同字典维数下重构图像的平均PSNR值

Table 2Average PSNR values of SR images with different dictionarysizes dB

图像64×2128×2256×2512×21024×2Man23.321523.362823.370723.414923.4359Face28.149028.173428.180728.193128.1960Flower33.180033.209033.280633.330633.3425Leaves22.248722.275122.351922.527122.6566Lena29.730929.748829.803329.865129.8995平均值27.326027.353827.397527.466227.5061与前者的差值0.02780.04370.06870.0399

表3不同字典维数下重构图像的平均时间
Table 3Average consuming time with different dictionary sizes

图像64×2128×2256×2512×21024×2Man14.1117.0522.4331.5456.33Face18.5221.8425.4835.9050.28Flower59.3065.6076.88112.11174.88Leaves25.2631.4341.7560.79121.24Lena61.5879.8797.06137.13234.83平均值35.7543.1652.7275.49127.51与前者的差值7.419.5622.7752.02

4.2LBP描述准确性及误差增量补偿分析

对大小为512×512的图像,计算以梯度特征及LBP码字重构纹理块的平均误差,分别为0.1755及0.0348,可见LBP码字的描述误差仅为梯度误差的19.82%,显然前者更准确地描述了纹理块.

同时,为比较高频预提升及误差增量补偿的有效性,用69幅自然图像构成训练集TS,其高频提升图像训练集为BTS,从TS和BTS中分别随机产生105个HR-LR块对,利用学习获得两个字典,表4示出了高频预提升重构图像的PSNR值.由表4可知,字典进行高频预提升后重构的PSNR值较未进行预处理情形平均提高0.1874dB .

表4常规字典与高频预提升字典重构图像PSNR比较
Table 4PSNR comparison of reconstructed images of regular and high frequency boost dictionarydB

图像TSETSFace34.196234.3502Flower37.338737.5120Lena35.379835.5609Rough30.753130.9181Grass28.537728.8014

4.3正则参数设置

图9　不同迭代步长和正则参数下图像重构的平均PSNR值 Fig.9　Average PSNR of reconstructed images with different iterations and regular parameters

4.4重构图像的质量比较

(a)HR梯度字典(b)LR梯度字典

(c)HR纹理字典(d)LR纹理字典

图10MFJD原子图

Fig.10Atom images of MFJD

图11-13分别示出了各算法重构图像的PSNR值、MSSIM值和FSIM值比较,横坐标为实验图序号.实验结果表明,MFJD-SCSR重构图像的PSNR值、MSSIM值及FSIM值比SCSR的有提升,说明重构灰度值更接近原图.总体上,SCSR、SDI-SCSR和MFJD-SCSR重构500幅标准图像的平均PSNR值分别为25.7368、25.9311及25.9792dB,平均MSSIM值分别为0.7497、0.7535及0.7540,平均FSIM值分别为0.8385、0.8453及0.8441.相比较原始的SCSR算法.MFJD-SCSR使PSNR值、MSSIM值及FSIM值分别提高0.2424dB、0.0043及0.0056，改进后的SDI-SCSR和MFJD-SCSR算法重构图像的灰度值精度有所提升,重构图像特征更接近于原始HR图像.其中:

图11　不同算法重构图像的PSNR值比较 Fig.11　PSNR comparison of reconstructed images of diffe-rent algorithms

图12　 不同算法重构图像的MSSIM值比较 Fig.12　MSSIM comparison of reconstructed images of diffe-rent algorithms

图13　不同算法重构图像的FSIM值比较 Fig.13　FSIM comparison of reconstructed images of different algorithms

(2)对强纹理结构图像,如Rough、Grass等,算法重构质量不理想,因为:①纹理结构复杂,在小区域内灰度变化较大,因此下采样LR图像的细节信息严重丢失,重构时需要估计更多信息；②采用自然图像建立的先验模型,不完全符合纹理图像的描述,模型失配必然导致重构结果失真.相反,MFJD-SCSR采用LBP纹理特征,原子匹配准确度和重构图像的PSNR优于原始SCSR算法,达0.4382～0.9142dB.

图14为3种算法对Rough图像进行4倍SR重构的结果和原HR图像.在SDI-SCSR和MFJD-SCSR重构的Rough图中,点状纹理更清晰,这是由于MFJD采用了LBP纹理块特征,重构时可以更准确地匹配字典原子.

(a)SCSR(b)SDI-SCSR(c)MFJD-SCSR (d)原始HR图像

图14Rough的4倍SR重构结果与原始HR图像

Fig.14Reconstructed results of Rough by a four times reconstruction and original HR image

4.5算法复杂度比较

SCSR、SDI-SCSR和MFJD-SCSR算法对500幅测试图像进行4倍SR重构时平均耗时分别为388.8、78.76及88.54s,MFJD-SCSR的耗时仅为SCSR的22.77%,重构速度明显提升.MFJD-SCSR比SDI-SCSR的重构时间减少10s左右,因为IBP算法仅简单计算图像差值,而MFJD-SCSR算法的BTV环节需计算图像移位后差值,因而重构速度减缓.

在上述实验中,SCSR、SDI-SCSR及MFJD-SCSR算法的选入加权原子数分别为1.459×106、2.882×105及2.903×105,MFJD-SCSR加权原子数目下降为SCSR的19.9%,加权复杂度大幅降低.SDI-SCSR及MFJD-SCSR算法加权原子数目接近,因为两者原子选入过程一致.MFJD-SCSR算法重构时间及选入原子数减少的原因是:①一方面MFJD-SCSR根据内容分类来选择字典,匹配效率得到提高；另一方面字典维数减少,待搜索原子数下降；②MFJD-SCSR提供纹理字典,且该字典维数较低,计算效率进一步提高.

5结论

文中提出一种多特征联合分级并用BTV正则优化的MFJD-SCSR算法,主要改进包括:①为改善SCSR单一字典寻找匹配原子效率低,分别构建了边缘块梯度特征和纹理块LBP字典,适用于不同的结构；②在同一种字典中采用树结构组织聚类原子,获得更快的匹配速度；③引入BTV正则项约束寻优,可改善图像边缘的振铃效应.实验结果表明,相比于原始SCSR算法,MFJD-SCSR改进算法使PSNR值提高0.2424dB,使MSSIM值和FSIM值分别提高0.0043、0.0056.此外,结构分类使字典维数降低,MFJD-SCSR的重构时间约为SCSR算法的22.77%,改善效果较明显.

参考文献：

[1]Ma Y,Zhang H,Xue Y.A novel super-resolution image reconstruction based on MRF [C]∥Proceedings of IEEE International Congress on Image and Signal Processing.Tianjin:IEEE,2009:1-4.

[2]Xi H,Xiao C,Bian C.Edge halo reduction for projections onto convex sets super resolution image reconstruction [C]∥Proceedings of IEEE International Conference on Digital Image Computing Techniques and Applications.Fremantle:IEEE,2012:1-7.

[3]Rasti P,Demirel H,Anbarjafari G.Iterative back projection based image resolution enhancement [C]∥Proceedings of IEEE Iranian Conference on Machine Vision and Image Processing.Zanjan:IEEE,2013:237-240.

[4]Lu X,Yuan Y,Yan P.Image super-resolution via double sparsity regularized manifold learning [J].IEEE Transactions on Circuits and Systems for Video Technology,2013,23(12):2022-2033.

[5]廖秀秀,韩国强,沃焱,等.基于流形学习和梯度约束的图像超分辨率重建 [J].华南理工大学学报:自然科学版,2012,40(4):8-15.

Liao Xiu-xiu,Han Guo-qiang,Wo Yan,et al.Super-resolution image reconstruction based on manifold learning and gradient constraint [J].Journal of South China University of Technology:Natural Science Edition,2012,40(4):8-15.

[6]Yang J,Wright J,Huang T S,et al.Image super-resolution via sparse representation [J].IEEE Transactions on Image Processing,2010,19(11):2861-2873.

[7]Yang J,Wang Z,Lin Z,et al.Coupled dictionary training for image super-resolution [J].IEEE Transactions on Image Processing,2012,21(8):3467-3478.

[8]Hao P,Kamata S.Maximum correntropy criterion for discriminative dictionary learning [C] ∥Proceedings of IEEE International Conference on Image Processing.Melbourne:IEEE,2013:15-18.

[9]Yang S,Wang M,Chen Y,et al.Single-image super-resolution reconstruction via learned geometric dictionaries and clustered sparse coding [J].IEEE Transactions on Image Processing,2012,21(9):4016-4028.

[10]Bai W,Yang S,Liu J,et al.Image super resolution using saliency-modulated context-aware sparse decomposition [C] ∥Proceedings of IEEE International Conference on Visual Communications and Image Processing.Kuching:IEEE,2013:1-6.

[11]Tropp J A,Wright S J.Computational methods for sparse solution of linear inverse problems [J].Proceedings of the IEEE,2010,98(6):948-958.

[12]Tian J,Chen L.Image noise estimation using a variation-adaptive evolutionary approach [J].IEEE Signal Processing Letters,2012,19(7):395-398.

[13]Xu J,Ding X,Wang S,et al.Background subtraction based on a combination of texture,color and intensity [C] ∥Proceedings of IEEE International Conference on Signal Processing.Beijing:IEEE,2008:1400 -1405.

[14]Tian J,Chen L.Bayesian stereoscopic image resolution enhancement [C] ∥Proceedings of 18th IEEE International Conference on Image Processing.Brussels:IEEE,2011:1505-1508.

[15]Needell D,Ward R.Stable image reconstruction using total variation minimization [J].SIAM Journal on Imaging Sciences,2013,6(2):1035-1058.

Improved SCSR Algorithm on the Basis of Flexible LBP Texture

Dictionary and Multi-Feature Description

MaLi-hongHuangYinLiJian-hui

(School of Electronic and Information Engineering∥National Engineering Techonology Research Center for Mobile Ultrasonic Detection,

South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:A multi-feature joint dictionary (MFJD) is suggested to improve the structural distinction in dictionary training and to accelerate the atom matching in sparse reconstruction.Firstly, two dictionaries branched respectively for edge- and texture-descriptions are created using gradient and LBP operators.Secondly, tree structures are introduced to represent the hierarchical clustering of atoms, which leads to a quick atom searching.Then, bilateral total variation (BTV) regularization is employed to achieve the optimal resolution.Experimental results show that, in comparison with the sparse coding super-resolution reconstruction (SCSR) algorithm, MFJD averagely improves the PSNR, MSSIM and FSIM of an image by 0.2424dB, 0.0043 and 0.0056, respectively, and reduces the reconstruction time to approximately 22.77% of that of SCSR algorithm owing to the reduction of dictionary dimensionality.

Key words: super-resolution reconstruction; structure classification; multi-feature description; LBP texture; bilateral total variation

Foundation items: Supported by the Open Research Project of the State Key Laboratory of Industrial Control Technology(ICT1434) and the Natural Science Foundation of Guangdong Province, China(S2013040014995)