摆线齿准双曲面齿轮实际齿面接触分析

摆线齿准双曲面齿轮实际齿面接触分析*

杜进辅1方宗德1高洪彪2张永振1赵国锐2

(1.西北工业大学 机电学院， 陕西 西安 710072;

2.中国第一汽车股份有限公司技术中心， 吉林 长春 130011)

摘要：为评估已加工的摆线齿准双曲面齿轮的啮合质量，基于实测齿面坐标点数据，用非均匀有理B样条(NURBS)曲面拟合离散点得到高度逼近真实齿面的数字化齿面，并依据空间啮合理论进行了数字化齿面的轮齿接触分析(TCA).与传统的滚检试验相比，该方法在获得实际齿面接触印痕的同时还可以获得传动误差曲线，比较全面地反映了实际齿面的啮合信息.最后通过比较某高速车桥齿轮副数字化齿面TCA与滚检试验结果，验证了文中方法的可行性.

关键词：摆线齿；准双曲面齿轮；轮齿接触分析；非均匀有理B样条

中图分类号：TH132.41

doi：10.3969/j.issn.1000-565X.2015.03.006

文章编号：1000-565X(2015)03-0041-08

收稿日期：2014-09-17

基金项目：* 国家自然科学基金资助项目(51305408, 51275180)；河南省高等学校重点科研项目(15A460029)

作者简介：贺占蜀(1985-),男, 博士,副教授,主要从事先进制造与精密加工研究. E-mail: hezhanshu@qq.com

延伸外摆线等高齿(摆线齿)准双曲面齿轮广泛应用于轿车以及客车的后桥中，具有加工效率高、运行平稳、强度高等优点[1-2].近年来，随着我国汽车工业的高速发展以及与欧美汽车企业的合作日益密切，先进的后桥摆线齿准双曲面齿轮加工工艺以及成套的加工、测量、磨刀、调刀设备逐步被引进到国内大型汽车企业，如一汽、中国重汽等.摆线齿准双曲面齿轮的应用越来越广泛，对其进行接触仿真、振动和强度性能分析具有重要意义，而基于高精度齿面的轮齿接触分析则是后续动力学特性和应力分析的基础.

轮齿接触分析(TCA)技术近年来有了较大发展[3-5].在切齿之前根据理论齿面的TCA评估啮合性能并据此修正加工参数，而后完成切齿再以实际齿面的滚检试验来验证啮合质量.但是滚检试验只能获得实际齿面的啮合印痕，而没有反映传动误差信息.大量研究已表明，传动误差直接影响齿轮副的动态性能，是导致振动和噪声的重要原因.因此如何全面地反映实际齿面的啮合性能显得尤为重要.

随着高性能齿轮测量中心的出现，复杂齿面的设计和检测走向数字化.王小椿等[6]用差曲面描述三坐标测量机测得的实际齿面与理论齿面的偏差，并提出了一种利用差曲面特征参数修正机床调整参数的方法.Zhang等[7]将理论齿面和误差曲面叠加获得了圆弧渐缩齿准双曲面齿轮的真实齿面.蒋进科等[8]用同样方法进行了修形斜齿轮实际齿面接触分析，但通过理论齿面和拟合所得的误差面叠加来表示实际齿面的计算过程繁琐，且最终还是没能脱离理论齿面.苏智剑等[9]通过仿真程序计算得到准双曲面齿轮离散的齿面点，然后用非均匀有理B样条(NURBS)拟合得到齿面.汪中厚等[10]提出了基于扫描式齿面测量的数字化真实齿面构建方法.张军辉等[11]研究了航空弧齿锥齿轮真实齿面的数字化仿真.但针对摆线齿准双曲面齿轮实测齿面点的拟合以及实际齿面TCA的研究却鲜有报道.

为此，文中基于齿轮测量中心测得的摆线齿准双曲面齿轮齿面点坐标数据，用二阶连续的双三次NURBS曲面拟合得到高度逼近真实齿面的数字化齿面，并依据空间啮合理论对其进行轮齿接触分析，获得了实际齿面的接触印痕以及传动误差，全面地反映了实际齿面的啮合信息.

1齿面测点的分布

运用齿轮测量中心进行齿面测量时，测点的分布直接影响后续齿面拟合的精度：测点越密，拟合精度越高，但用时过长却又影响效率.格里森公司的经验是一般取45个测点，即齿高方向5个，齿长方向9个.文中采用克林贝格公司的P65齿轮测量中心，选取225个测点，即齿长和齿高方向各15个，如图1所示，e表示齿高方向，f表示齿长方向.

图1　测点分布图 Fig.1　Distribution diagram of measuring points

2实际齿面的NURBS表示

二阶连续的双三次NURBS曲面表达式s(e,f)可写成如下形式[12]：

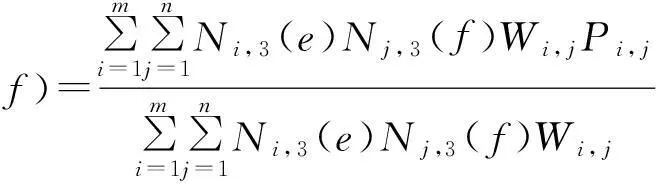
(1)

式中：m、n分别为e、f向的控制顶点个数；Pi,j为曲面的控制顶点；Wi,j为Pi,j的权因子，文中各点取相同值；Ni,3、Nj,3分别为e、f向的三次B样条基函数.

根据测点数据先由e(f)向计算得到各条NURBS曲线的控制顶点，再以求得的控制顶点作为新的型值点沿f(e)向计算，得到所有NURBS曲面的控制定点，带入式(1)即可获得双三次NURBS曲面.从齿轮测量中心获得的齿面数据通常不在边界上，通过对外插值，可以将数据延伸到齿面有效边界，这对反算的控制矩阵影响很小，因此可以保证齿面接触分析的精度.

根据上面方法，以某高速车桥齿轮副为例(基本参数见表1)，获得工作面(小轮凹面，大轮凸面)的双三次NURBS曲面及其控制顶点网格如图2和图3所示，非工作面(小轮凸面、大轮凹面)用同样方法获得.

表1齿轮副基本参数Table1Basicparametersofgearpair

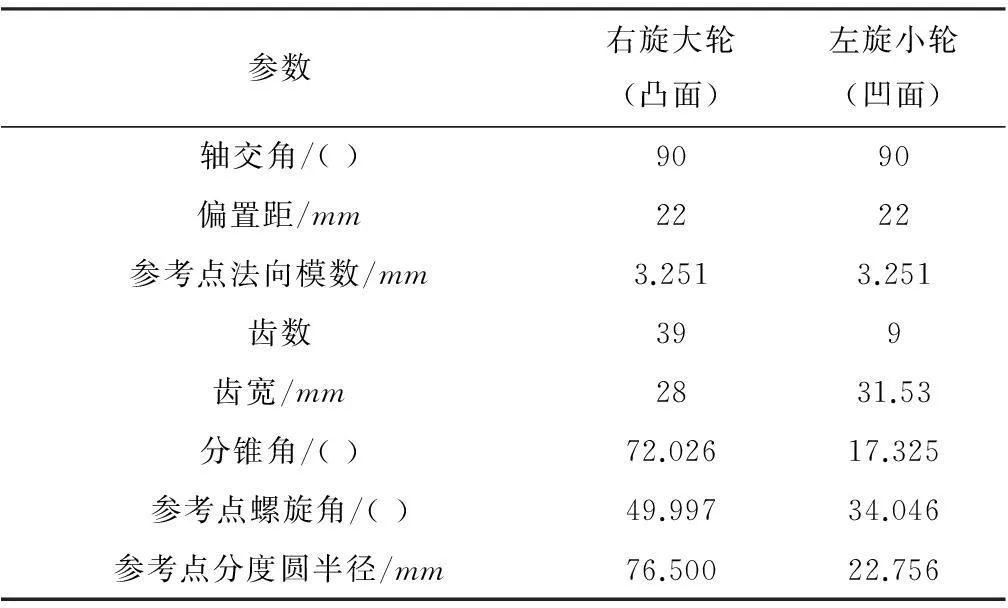
参数右旋大轮(凸面)左旋小轮(凹面)轴交角/()9090偏置距/mm2222参考点法向模数/mm3.2513.251齿数399齿宽/mm2831.53分锥角/()72.02617.325参考点螺旋角/()49.99734.046参考点分度圆半径/mm76.50022.756

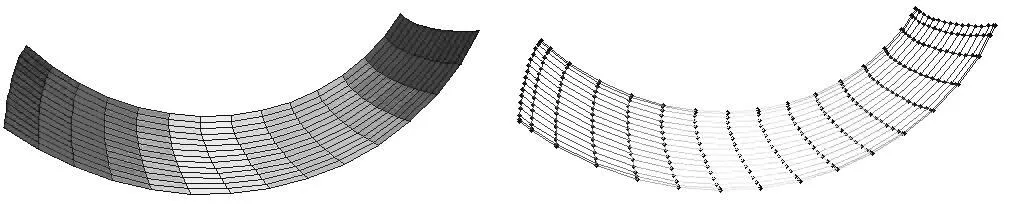
( a) NURBS曲面　　　　　　　( b)控制网格

( a) NURBS曲面　　　　　　　( b)控制网格

最后经过插值反算得到逼近实际齿面的数字化齿面：

Ri=Ri(ui,vi),i=1,2

(2)

式中：1表示小轮；2表示大轮；u、v为曲面参数.

获得如式(2)所示数字化齿面之后，即可计算得到各点的位矢、法矢、切矢、主曲率和主方向，为实际齿面的TCA做好准备.

由于NURBS曲面为构造齿面，构造齿面上各点除控制顶点外，其他位置均由拟合算法计算所得，因此必须对NURBS拟合精度进行验证，步骤如下：

(1)按上述同样规律在相同范围内取其理论齿面上15×15个点，拟合得到理论齿面的数字化齿面；

(2)求出理论齿面上所取15×15个点中所有相邻4个点构成的最小曲面片的中点(14×14个点)；

(3)计算理论齿面上这些中点与其对应的数字化齿面上的点的法向距离，其中最大法向距离即为最大拟合误差；

(4)取每列法向距离中的最大值绘制曲线，结果如图4所示.

图4　拟合误差曲线 Fig.4　Curves of fitting error

可见小轮拟合误差较大，但大小轮最大拟合误差均不超过0.1μm，因此可以用拟合得到的数值化齿面代替实际齿面进行TCA.

3实际齿面接触分析

如图5所示，两配对实际齿面的位矢、法矢以及切矢分别位于固定于小轮和大轮的坐标系S1、S2中，H1、H2分别为小轮和大轮的轴向装配距离，Σ为轴交角，V为小轮偏置距.通过坐标变换，将其表示在机床坐标系Ss中：

(3)

(4)

图5　摆线齿准双曲面齿轮啮合坐标系 Fig.5　Mesh coordinates of cycloid tooth hypoid gear

式中，r、n、t分别为位矢、法矢和切矢，φ1、φ2分别为小轮和大轮转角，Ms1、Ms2为坐标系Si(i=1,2)到机床坐标系Ss的转换矩阵,Ls1、Ls2分别为Ms1、Ms2的左上角3×3子矩阵.Sp、Sq、Sr为辅助坐标系.

实际齿面的TCA是求解两配对齿面在接触点处位矢和法矢所满足的如下方程组[13]：

(5)

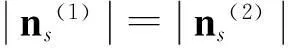
(6)

或

(7)

ns(i)×ts(i)和ts(i)(i=1,2)是大小轮切平面内两相互垂直的向量.方程组(6)或(7)包含5个独立的标量方程，6个未知量，以小轮旋转角度φ1为输入，则方程组得解；不同的φ1对应不同的啮合位置,在数字化齿面有效边界内所求得的所有瞬时接触点即构成齿面接触轨迹.其传动误差ΔE可由下式计算得出：

(8)

式中，φ10、φ20分别为小轮和大轮在参考点啮合时的初始转角，Z1、Z2分别为小、大轮齿数.

4算例与试验验证

为验证文中方法，仍以上面某高速车桥齿轮副为例，基本参数如表1所示，用奥利康C28数控(CNC)铣齿机进行加工，如图6所示，经过热后研齿，用克林贝格P65齿轮测量中心进行齿面测量(如图7所示)，得到的大轮和小轮的测量齿面相对于理论齿面的误差如图8和图9所示.

图6　C28数控铣齿机 Fig.6　C28 CNC milling machine

图7　大轮齿面测量 Fig.7　Measurement of tooth surface

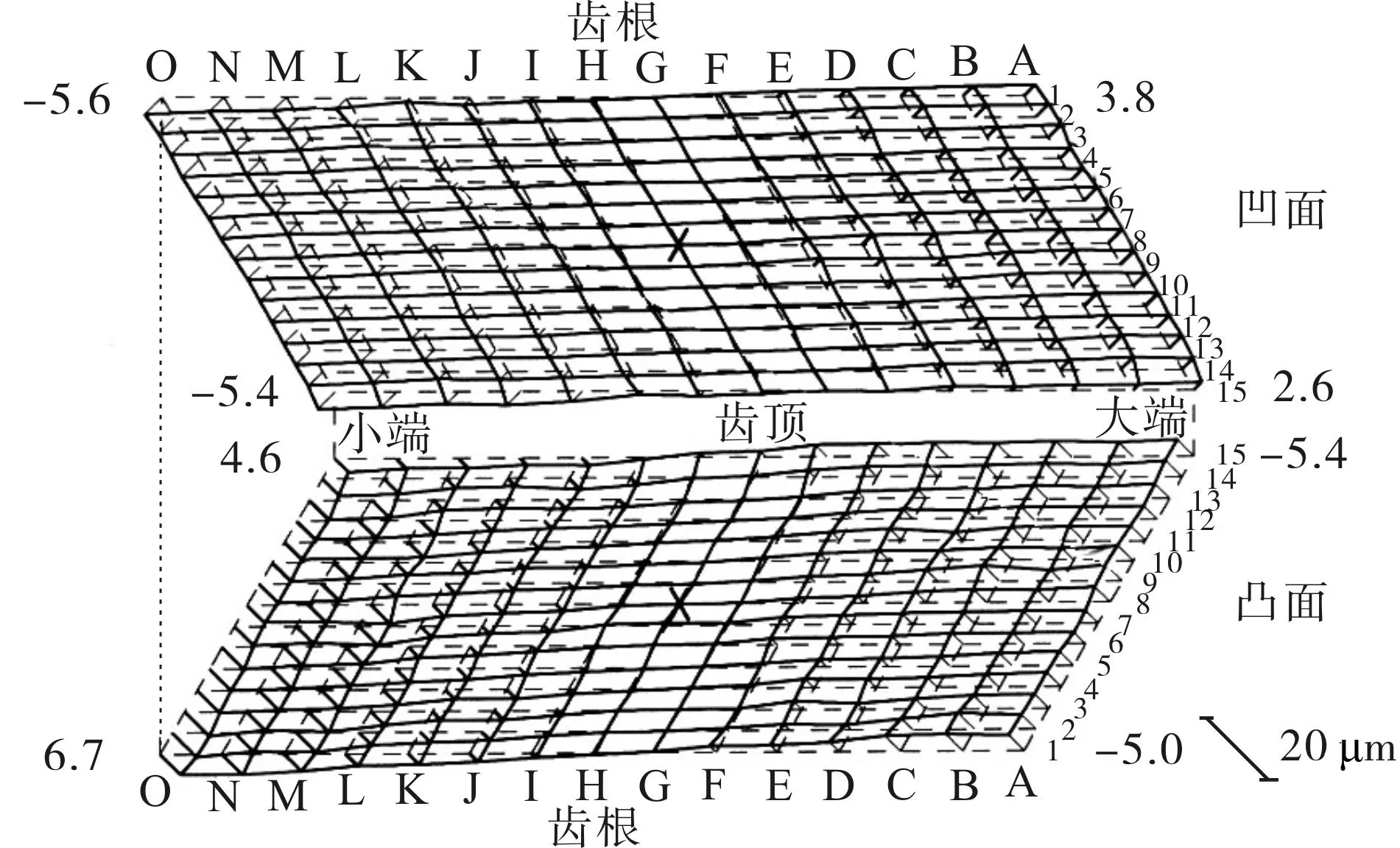
图8　大轮测量齿面相对于理论齿面的误差 Fig 8　Deviations between measurement and theoretical gear tooth surface

图9　小轮测量齿面相对于理论齿面的误差 Fig.9　Deviations between measurement and theoretical pinion-tooth surface

按照前文方法，将测量获得的实际齿面离散点拟合成双三次NURBS曲面，进行数字化齿面TCA，(研磨齿面取弹性变形量δ为0.00381mm[14])，得到齿面的接触印痕和传动误差如图10所示.可见大轮凸面接触区分布在齿宽方向32.4%～74.9%，凹面接触区分布在齿宽方向27.4%～66.3%，齿高方向分布在齿顶与齿根过渡线之间，凸面印痕较凹面稍宽且接触迹线倾斜较大.将实际齿轮副在滚检机上进行滚检试验(如图11所示)，得到滚检印痕如图12

( a)大轮凸面接触印痕

( b)大轮凹面接触印痕

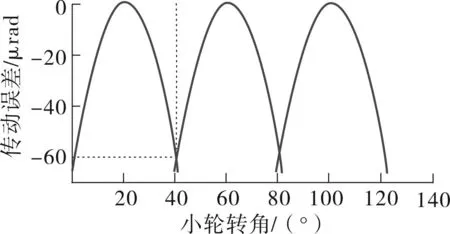
( c)工作面传动误差

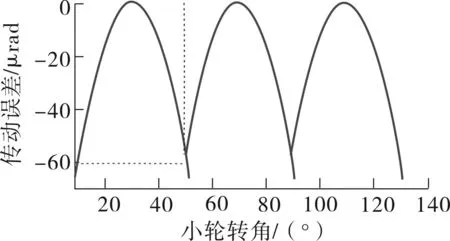
( d)非工作面传动误差

所示，可见两面接触区位置均分布在齿宽中部1/3区域，凸面接触区较倾斜且较凹面宽，两面滚检印痕的形状与仿真分析结果也基本一致.故认为本方法是可行的.

图11　滚检试验 Fig.11　Rolling test experiment

( a)凸面

( b)凹面

5结论

基于摆线齿准双曲面齿轮实测齿面坐标点数据，拟合得到了高度逼近实际齿面的摆线齿准双曲面齿轮数字化齿面.编制了摆线齿准双曲面齿轮实测齿面数据点拟合以及TCA通用计算机程序，将其集成到齿轮测量中心的数据处理程序中，以实际齿面的TCA代替传统的滚检，较全面地反映了实际齿面的啮合信息，弥补了传统滚检试验只能获得接触印痕而无法获得传动误差的不足，为后续高精度的动力学特性分析以及应力计算打下了基础.以某高速车桥齿轮副为例进行了试验验证，结果表明文中方法获得的数字化齿面的接触印痕与滚检试验印痕基本一致，证明了文中方法的可行性.这种方法既节省了检验设备又缩短了生产周期，并且由于上述计算过程的通用性，经推广后同样适用于其他类型齿轮传动.

参考文献：

[1]邓效忠,郭建松.适合中国国情的等高齿锥齿轮制造技术[J].现代零部件,2011(9):62-63.

DengXiao-zhong,GuoJian-song.Uniform-depthbevelgearmanufacturingtechnologythatsuitstheChina’snationalconditions[J].ModernComponents,2011(9):62-63.

[2]董学朱.摆线齿锥齿轮及准双曲面齿轮设计和制造[M].北京:机械工业出版社,2002：335- 336.

[3]FanQ,LowellW.Newdevelopmentsintoothcontactanalysis(TCA)andloadedTCAforspiralbevelandhypoidgeardrives[J].GearTechnology,2007,5:26-35.

[4]MohammadQAbdullah,NassearRHmoad.Generationandtoothcontactanalysis(TCA)ofhypoidgeardrive[J].JournalofEngineering,2012,18(3):320-339.

[5]FanQ.ComputerizedmodelingandsimulationofspiralbevelandhypoidgearsmanufacturedbyGleasonfacehobbingprocess[J].JournalofMechanicalDesign,2006,128(11):1315-1327.

[6]王小椿,王军,姜虹，等.螺旋锥齿轮的齿面测量及机床加工参数修正[J].机械工程学报,2003,39(8):125-128.

WangXiao-chun,WangJun,JiangHong,etal.Toothsurfacemeasurementandmachine-settingscorrectionofspiralbevelgear[J].ChineseJournalofMechanicalEngineering,2003,39(8):125-128.

[7]ZhangY,LitvinFL.Computerizedanalysisofmeshingandcontactofrealtoothsurfaces[J].JournalofMecha-nicalDesign,1994,116(9):667-682.

[8]蒋进科,方宗德,苏进展.斜齿轮实际齿面接触分析技术[J].西北工业大学学报,2013,31(6):921-925.

JiangJin-ke,FangZong-de,SuJin-zhan.Toothcontactanalysis(TCA)ofrealhelicalgeartoothsurface[J].JournalofNorthwesternPolytechnicalUniversity,2013,31(6):921-925

[9]苏智剑,吴序堂,毛世民，等.基于齿面参数化表示的准双曲面齿轮的设计[J].西安交通大学学报,2005,39(1):17-20.

SuZhi-jian,WuXu-tang,MaoShi-min,etal.Designofhypoidgeartoothsurfacerepresentedbynon-uniformrationalb-splinepolynomial[J].JournalofXi’anJiaotongUniversity,2005,39(1):17-20.

[10]汪中厚,李刚,久保爱三.基于数字化真实齿面的螺旋锥齿轮齿面接触分析[J].机械工程学报,2014,50(15):1-11.

WangZhong-hou,LiGang,KuboAizoh.Toothcontactanalysisofspiralbevelgearsbasedondigitalrealtoothsurfaces[J].JournalofMechanicalEngineering,2014,50(15):1-11.

[11]张军辉,方宗德,王成.基于NURBS的弧齿锥齿轮真实齿面的数字化仿真[J].航空动力学报,2009,24(7):1672-1676.

ZhangJun-hui,FangZong-de,WangCheng.Digitalsimulationofspiralbevelgears’realtoothsurfacesbasedonnon-uniformrationalB-spline[J].JournalofAerospacePower,2009,24(7):1672-1676.

[12]朱心雄.自由曲线曲面造型技术[M].北京：科学出版社，2001:88-168.

[13]LitvinFL.Geargeometryandappliedtheory[M].Englewood：PrenticeHall,1994:268-272.

[14]FanQ.Enhancedalgorithmsofcontactsimulationforhypoidgeardrivesproducedbyface-millingandface-hobbingprocesses[J].JournalofMechanicalDesign,2007,129:31-37.

[15]Litvin,FL,ShevelevaGI,VecchiatoD,etal.Modifiedapproachfortoothcontactanalysisofgeardrivesandautomaticdeterminationofguessvalues[J].ComputerMethodsinAppliedMechanicsandEngineering,2005,194:2927-2946.

ContactAnalysisofRealToothSurfaceofHypoidGearwith

CycloidTooth

Du Jin-fu1FangZong-de1GaoHong-biao2ZhangYong-zhen1ZhaoGuo-rui2

(1.SchoolofMechanicalEngineering,NorthwesternPolytechnicalUniversity,Xi’an710072,Shaanxi,China;

2.R&DCenter,ChinaFAWCo.,Ltd.,Changchun130011,Jilin,China)

Abstract:In order to evaluate the meshing quality of real hypoid gear with cycloid tooth, firstly, the digital gear surfaces that exactly approximate real tooth surfaces are obtained by fitting the measured discrete points with non-uniform rational B-spline (NURBS) curve. Then, on the basis of space meshing theory, a tooth contact analysis (TCA) of digital gear surfaces is carried out, which provides contact patterns the same as the traditional rolling test and transmission error curves that can not be obtained from the traditional test. As a result, actual meshing information can be relatively fully reflected. Finally, the feasibility of the proposed method is verified through a comparison between digital gear surface TCA and rolling test of a high-speed axle gear pair.

Keywords：cycloidtooth;hypoidgear;toothcontactanalysis;non-uniformrationalB-spline

Foundationitems:SupportedbytheNationalNaturalScienceFoundationofChina(NSFC)(51305408, 51275180)