基于扩展Prony算法的平坦快衰落信道预测算法

基于扩展Prony算法的平坦快衰落信道预测算法*

仲伟志仲丹丹井庆丰刘鑫

(南京航空航天大学 航天学院， 江苏 南京 210006)

摘要：针对最大熵方法(MEM)存在的迭代计算量大和误差扩散的问题，以及ESPRIT算法存在的平坦快衰落信道预测精度受制于自相关函数估计的问题，文中提出基于扩展Prony算法的平坦快衰落信道预测算法.扩展Prony算法通过最小二乘法拟合和计算高次代数方程来求复根，无需估计自相关函数且可批量计算，能够提高预测精度和运算效率.理论和仿真结果表明，扩展Prony算法较MEM和ESPRIT算法具有更高的预测精度，同预测精度下具有3～5dB的信噪比优势，且算法性能稳定，运算效率高.

关键词：衰落信道；预测；MEM算法；ESPRIT算法；扩展Prony算法

中图分类号：TN929.5

doi：10.3969/j.issn.1000-565X.2015.03.012

文章编号：1000-565X(2015)03-0084-06

收稿日期：2014-08-05

基金项目：* 国家自然科学基金资助项目(61072067，61372076)；高等学校学科创新引智计划项目(B08038)；综合业务网理论及关键技术国家重点实验室专项基金资助项目(ISN1001004)

作者简介：李东武(1981-)，男，博士生，主要从事通信信号处理研究.E-mail: dongwuli@163.com

随着现代无线移动通信的快速发展,人们对无线通信系统传输能力的要求不断提高,希望能高速传输大量数据和多媒体等信号.但无线移动通信的信道使系统传输性能受到很大限制.发射端和接收端之间的信道环境由于地形和人为等因素变得十分复杂,多径效应和多普勒频移导致接收信号幅度和相位发生较大畸变,严重影响通信性能.

为提高系统传输性能,研究者提出一些新的自适应传输技术,如自适应调制[1]、自适应编码[2]、自适应功率控制[3]等.这些自适应传输技术通过跟踪信道环境来调整调制方式、传输速率、传输功率、天线增益等.

为实现这些自适应传输方法,传输过程中的信道状态信息(CSI)必须已知,CSI通过接收端信道估计得到,并反馈到发射端,发射端利用这些反馈信息来调整自适应传输参数,从而提高传输效率.信道状态信息CSI的反馈延迟会影响自适应传输方法的设计,在慢衰落信道情况下,对CSI反馈时间要求不高,但在快衰落信道情况下,反馈时延过长会导致自适应传输系统性能急剧下降.因此,对于快衰落信道实现自适应传输时,需要辅助采用信道预测技术,并且如何提高预测精度和预测长度成为研究者关注的首要问题.

目前针对平坦时变衰落信道的预测算法主要包括最大熵方法(MEM)[4]、ESPRIT算法[5]、长距离预测法[6]、root-MUSIC[7]方法、利用卡尔曼滤波器实现均衡器方法[8]、非线性Volterra自适应预测法[9]、基于频域神经网络的信道预测[10]等.Root-MUSIC方法适用于谐波组合模型,类似ESPRIT算法,对于模型匹配要求较高.非线性Volterra算法对于非线性滤波器有一定的要求,并存在滤波器阶数选择、收敛速度和算法精度兼顾等问题.当采样时间间隔不足够大时,长距离算法会产生模型不匹配的情况,影响预测性能,多步预测时会产生误差扩散.MEM预测算法中采用Burg迭代算法,计算量较大,且多步预测时以预测值代替真实值引起误差扩散.ESPRIT算法理论上可以实现没有误差扩散的多步预测,但是本质上,它的精度受制于自相关函数估计.MEM方法及ESPRIT算法性能较稳定、精确度高,易于实现,因此,作为经典预测算法,被研究者广泛采用.针对以往算法的不足,文中提出基于扩展Prony算法的信道预测算法,该算法通过高次代数方程计算信号极点,无需估计自相关函数,并使用修正的法方程,保证了该算法的稳定性,提高了算法的精度.

1衰落信道模型

考虑平坦衰落信道,其接收信号低通复值模型[4]如下：

γ(t)=c(t)s(t)+w(t)

(1)

式中：t为时间,c(t)是平坦衰落系数,为乘性；s(t)为传输信号；w(t)为加性高斯白噪声(AWGN).

在移动衰落信道环境下,衰落系数c(t)由N个多普勒频移信号的和给出[11]：

(2)

式中：An为对应于第n个散射信号的幅度,fn为多普勒频率,φn为相位.多普勒频率表达式为

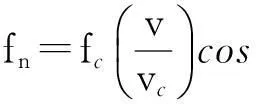
(3)

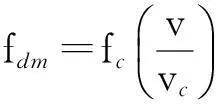
由模型可知,在预测衰落系数c(t)时,将其分解为N=9个散射成分,可以准确描述信道特性[4].若散射信号(2)中的参数An、fn和φn已知且恒定,便可准确预测出c(t).但在实际中,参数An、fn和φn并不能已知,且随着时间的推移,三者会缓慢变化.因此,在进行信道预测时,只考虑短时间内衰落,即给定数据分组的传播特性不会显著改变,进而可以假定模型中的参数缓慢变化或者是保持不变.

经过匹配滤波和采样,在输出端得到离散时间系统模型，表示为

yk=ckbk+wk

(4)

式中,ck是衰落系数c(t)以数据率进行采样的第k个采样间隔上的采样值,bk为数据序列,wk是离散加性高斯白噪声.一般情况下,c(t)和ck可视为复高斯随机过程,其幅度服从瑞利(Rayleigh)分布,相位服从均匀分布[11].

对信道采样时,采样频率满足奈奎斯特采样定理,信道采样频率fs≥2fdm,而非直接采用数据速率对信道采样.这是一种合理且高效的方法,可以提高预测距离,降低预测复杂度[12].信道采样频率远远低于数据速率,为得到更确切的仿真效果,这里需要采用插值方法[4]对预测出的数据进行插值,拟合相邻数据之间的未通过预测算法手段得到的数据,以得到数据速率上的衰落信道系数预测值.如果直接以数据速率对信道系数进行采样(过采样),预测时要求的数据数量将大幅增加,运算复杂度将大大提升.经典的插值算法包括线性插值、多项式插值、基于离散傅里叶变换(DFT)插值、样条插值等方法,文中选择插值方法取代过采样进行预测工作.结合插值算法的信道预测算法与其他几种常用插值算法的比较将在仿真实验部分体现.

2最大熵方法和ESPRIT算法

最大熵谱估计是由Burg在1967年提出的现代谱分析法[13],该方法仿照连续随机变量熵定义了功率谱的熵,功率谱估计时使得功率谱熵最大.经证明[14],Burg最大熵功率谱可以与自回归(AR)功率谱等价；因此，最大熵方法采用全极点模型,或者是AR模型,在进行谱分析时有很好的谱线特征,对应于衰落信道的多径分量[15].

在对衰落信道系数做线性预测时,全极点的频率响应模型表示如下：

(5)

式中,p是模型阶数,系数hj对应线性预测系数,z代表极点.根据自回归的性质,衰落信道系数的预测值可表示为

(6)

为得到频率响应模型中的线性预测系数hj,采用Burg算法,根据最小均方误差(MMSE)准则,使前、后向预测误差的平均功率最小,以Levinson递推作约束求出AR模型参数估计值[14],即得到线性预测系数hj,j=1,2,…,p.

在信道预测中,MEM方法利用观测数据直接计算AR模型参数,免去求自相关函数的步骤,综合考虑前向与后向预测误差并使之平均功率最小,有很高的预测精度.但是对于一组观测数据,MEM方法仅能进行一步预测,多步预测时需要用已预测的数据代替真实数据进行计算,于是会造成误差的累积与扩散.

针对MEM算法的不足,为更好地利用模型自身的特点,联系关于复正弦信号和形式的信号谱估计,研究者提出采用旋转不变技术估计信号参数(ESPRIT)算法来对平坦快衰落信道进行预测.作为现代信号处理中的主要方法,ESPRIT算法优势在于用特征值确定谐波频率,计算量不高,算法基于最小二乘(LS)准则,算法精度可靠.

ESPRIT算法取两个时间上相互位移的数据集，由其张成的信号子空间有旋转不变性,通过广义特征值估计复正弦信号的频率,可以对采样数据矩阵进行奇异值分解从而实现估计[5].

基于ESPRIT算法的衰落信道预测可描述如下,对信道模型(2)进行变形,令

(7)

这样,衰落信道系数的采样值可表示为

(8)

由于模型中已假设幅度An、多普勒频移fn及相位φn短时间内看作不变,上式中只需确定这3个参数,即对an、zn给出估计,并以此计算未来c(k),k=M+1,M+2,…完成预测.现在的问题转化为用ESPRIT算法估计噪声中复正弦信号的频率和幅度.文中使用采样数据奇异值分解的ESPRIT算法,由信道系数采样数据得到信号子空间,根据奇异值确定对应的散射信号分量数目.从信号子空间中获得信号极点的估计(包含频率信息),而后根据信号极点的估计值来估计幅度.

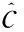
ESPRIT算法预测衰落信道时,充分利用模型特性,并估计固定参数,理论上可以避免多步预测的误差扩散.但是由于该算法本质上依赖对数据自相关函数的估计,故而极点估计的精度受限制.

3扩展Prony算法与改进的信道预测算法

针对MEM方法和ESPRIT算法的一些不足,文中提出采用扩展Prony(EP)算法来进行平坦快衰落信道预测.作为一种功率谱估计方法,文献[16]利用传统的Prony方法进行信道预测工作；经过扩展的Prony算法[17]能从均匀采样信号中提取有价值的信息,可分解出一系列按指数衰减的正弦信号.相较于传统Prony方法,扩展的Prony算法精度有所保证,并在未知散射信号数目的情况下有更大的可行性.

扩展Prony算法需要计算最小二乘法拟合和高次代数方程求复根.极点的估计并不依赖于自相关函数的估计,而是与数据本身有关；可利用信道模型特性将其与常系数线性差分方程联系起来,而这里的差分方程是一个特殊的AR过程.根据AR参数可以做频率估计,即确定极点,进而确定相应幅度.算法避免了大的计算量,同时对频率与幅值的估计方差小.

衰落信道系数的采样值如式(8)所示,其估计值表示为

(9)

(10)

定义特征多项式:

(11)

式中d0=1.位于根zi处的ψ(zi)=0可使得式(10)成立.因此如果能够得到参数di的估计,然后根据特征多项式估计出极点,再由极点估计出幅值就可以对未来信道系数作预测.

为得到di的最小二乘估计,可列出EP方法的扩展阶的法方程形式：

Red=re

(12)

式中，

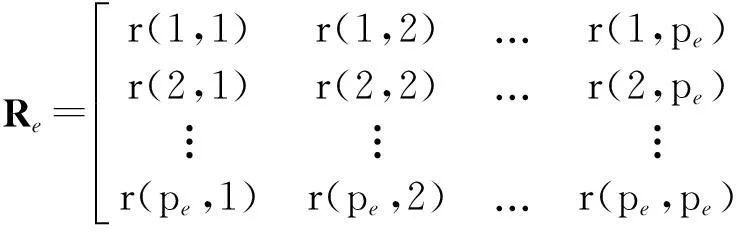
(13)

(pe≫p)

(14)

(15)

式中，样本函数r(i,j)可以称作修正协方差函数,考虑使前向和后向预测误差平均值最小,将其表示如下：

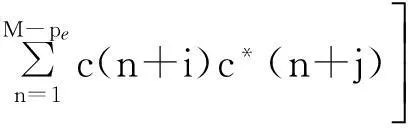
(16)

确定矩阵Re的有效秩p,进而可得到d1,d2,…,dp的最小二乘估计.然后,可求出特征多项式

1+d1z-1+…+dpz-p=0

(17)

的根zi,i=1,2,…,p,zi称为Prony极点,完成了对信号频率的估计.

估计幅值过程与ESPRIT算法类似,计算幅值的最小二乘解a1,a2,…,ap.式(9)中的极点zn和幅值an都有了估计值,将k=M+1,M+2,…带入式(9)中,完成信道衰落系数的预测.

利用EP算法预测衰落信道系数的步骤如下:

(1)利用式(16)计算样本函数r(i,j),构造扩展阶矩阵(13)；

(2)确定Re的有效秩p,根据式(12)得到d1,d2,…,dp的最小二乘估计；

(3)求特征多项式(17)的根,完成极点估计；

(4)利用式(9)列出方程

(18)

解得关于幅度的最小二乘估计a1,a2,…,ap；

(5)将k=M+1,M+2,…带入式(9)中(必要时进行插值工作),完成信道衰落系数的预测.

EP算法利用了信道模型的自身特征,利用了采样数据本身,性能无需受制于自相关函数的估计,且使用修正的协方差函数减小了噪声引起的谱峰移动,精度较高.另外,算法不需要求解特征方程，无迭代过程,只需求解齐次线性方程,计算量较MEM和ESPRIT算法小.

4仿真结果与分析

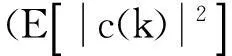
3种算法的幅值预测误差如图1所示,仿真时信道系数采样频率fs=200Hz,利用100个采样数据点进行一步预测.其中,MEM方法线性预测阶数为30.

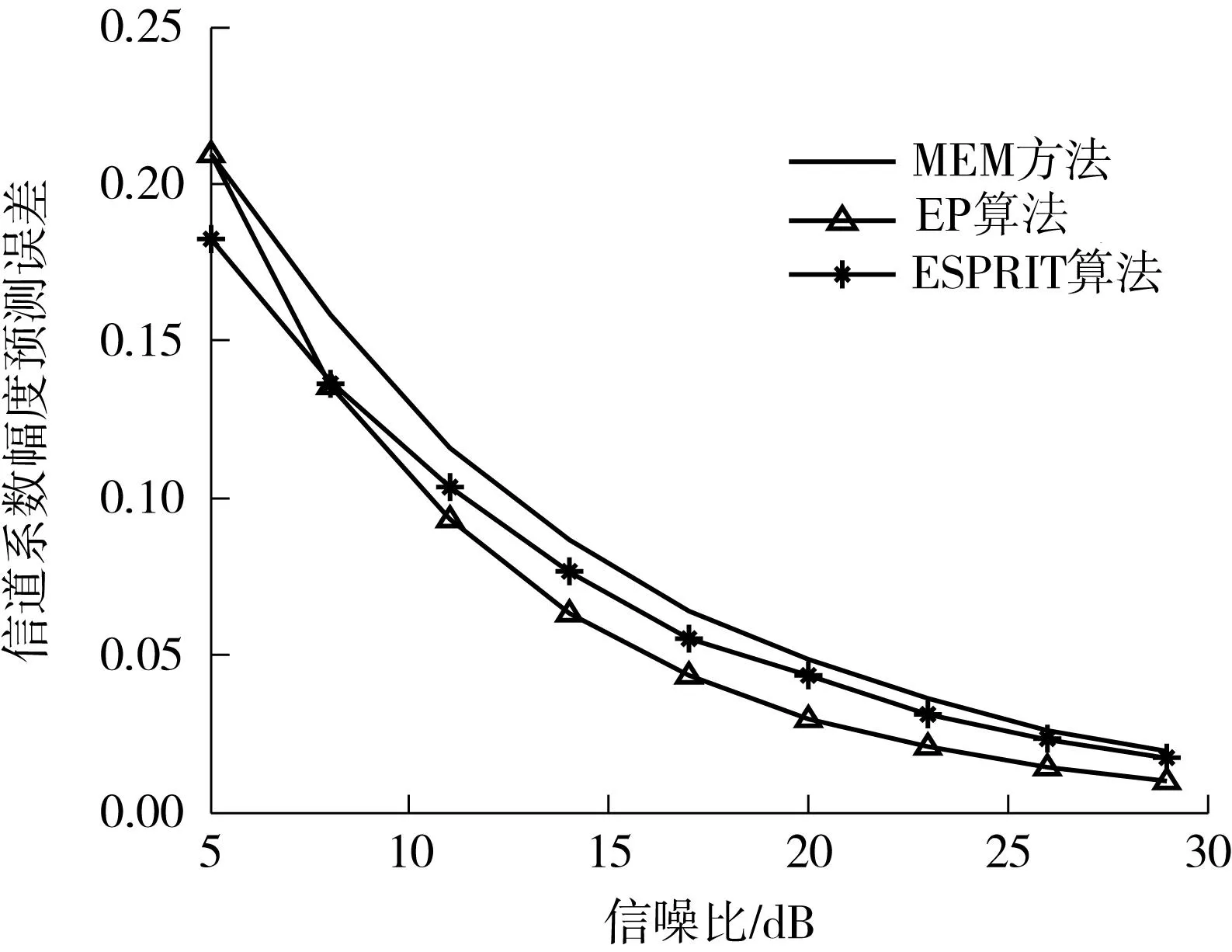
图1　3种算法预测效果比较 Fig.1　Comparison of prediction performance among three algorithms

如图1所示,随着信噪比(SNR)增加,算法精度都相应提高,EP算法预测平均误差小于另两种算法.MEM方法对噪声较为敏感,噪声条件下的MEM谱估计的AR模型不再是全极点模型,频谱估计产生偏差,故在信噪比较低时,MEM方法预测精度较低；与之类似,当信噪比较低时,EP算法对极点的估计受到AR模型的影响,算法性能不如ESPRIT算法.由于ESPRIT和EP算法通过求解信道系数中的短时不变量来进行预测,同时可保证极点与幅度的预测精度,具有优于MEM方法的预测性能.ESPRIT算法精度受到自相关函数估计的影响,EP算法无此限制,随着信噪比增加,其预测精度优于另两种算法,可以看出在同一预测精度条件下,EP算法有3～5dB的信噪比优势.

采用100个信道系数采样数据点,信道采样频率为200Hz,预测未来15个点(以采样间隔为单位)，结果可见图2.由图可见,随着预测距离增加,预测平均误差整体呈增加趋势,这是因为，衰落信号具有长期不可预测性,随着时间的推移,数据的相关性变差.EP算法的预测精度明显高于另两种算法,预测的稳定性高.由于EP算法是进行批量计算的算法,在一定精度范围内,可以一次性获取可靠的多步预测结果,时效性高.

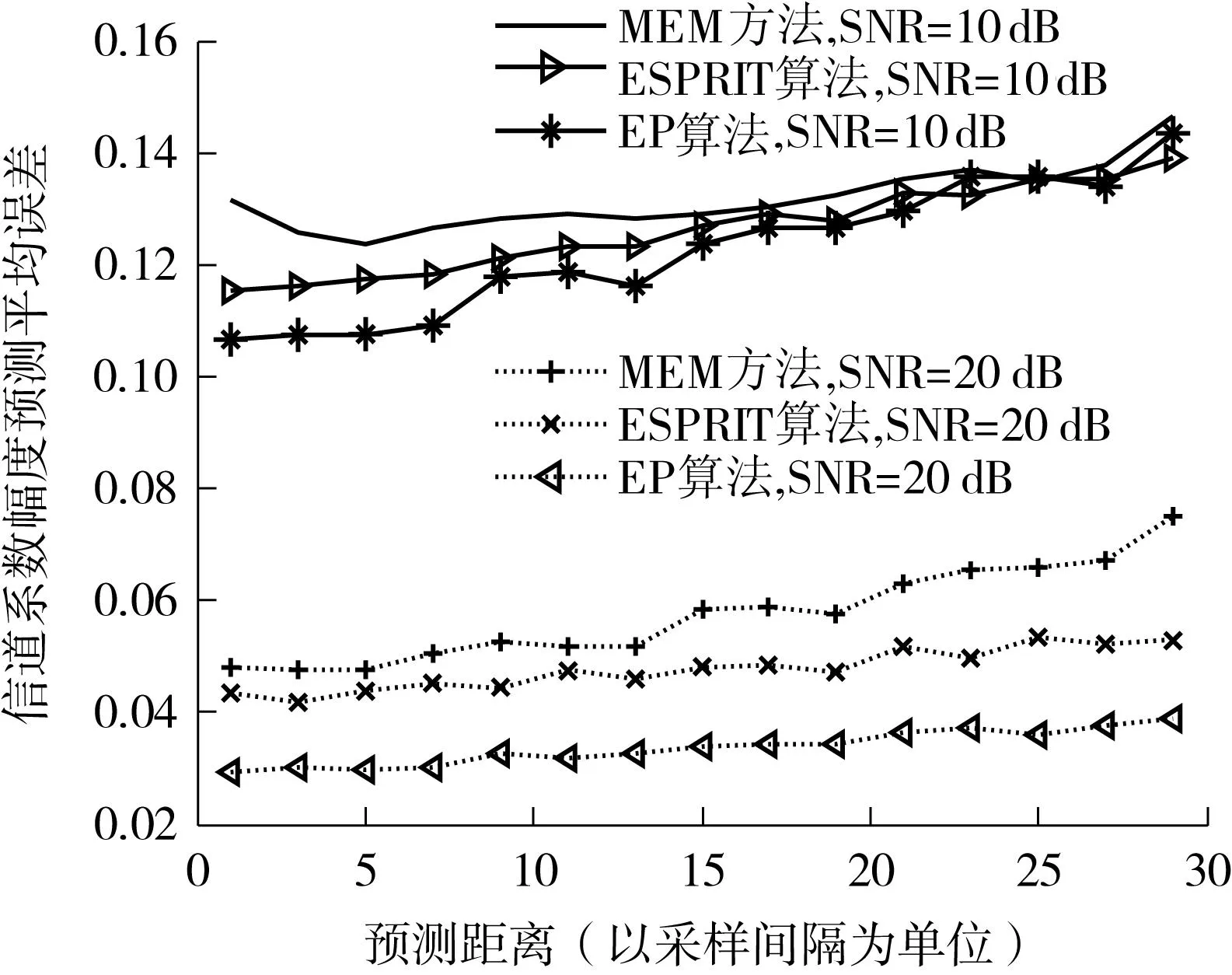
图2　3种算法预测平均误差随预测距离的变化 Fig.2　Changes of mean error of three algorithms with prediction range

由于插值对信道系数预测有重要意义,图3给出了基于3种常用插值算法(即三次样条插值、线性插值和三次多项式插值)的预测误差.仿真采用EP算法,信号数据传输速率为200kb/s,信道系数采样频率fs=200Hz,利用100个采样数据点预测未来30个数据,对预测的这30个数据进行插值,计算所有预测出的信道系数的平均误差.

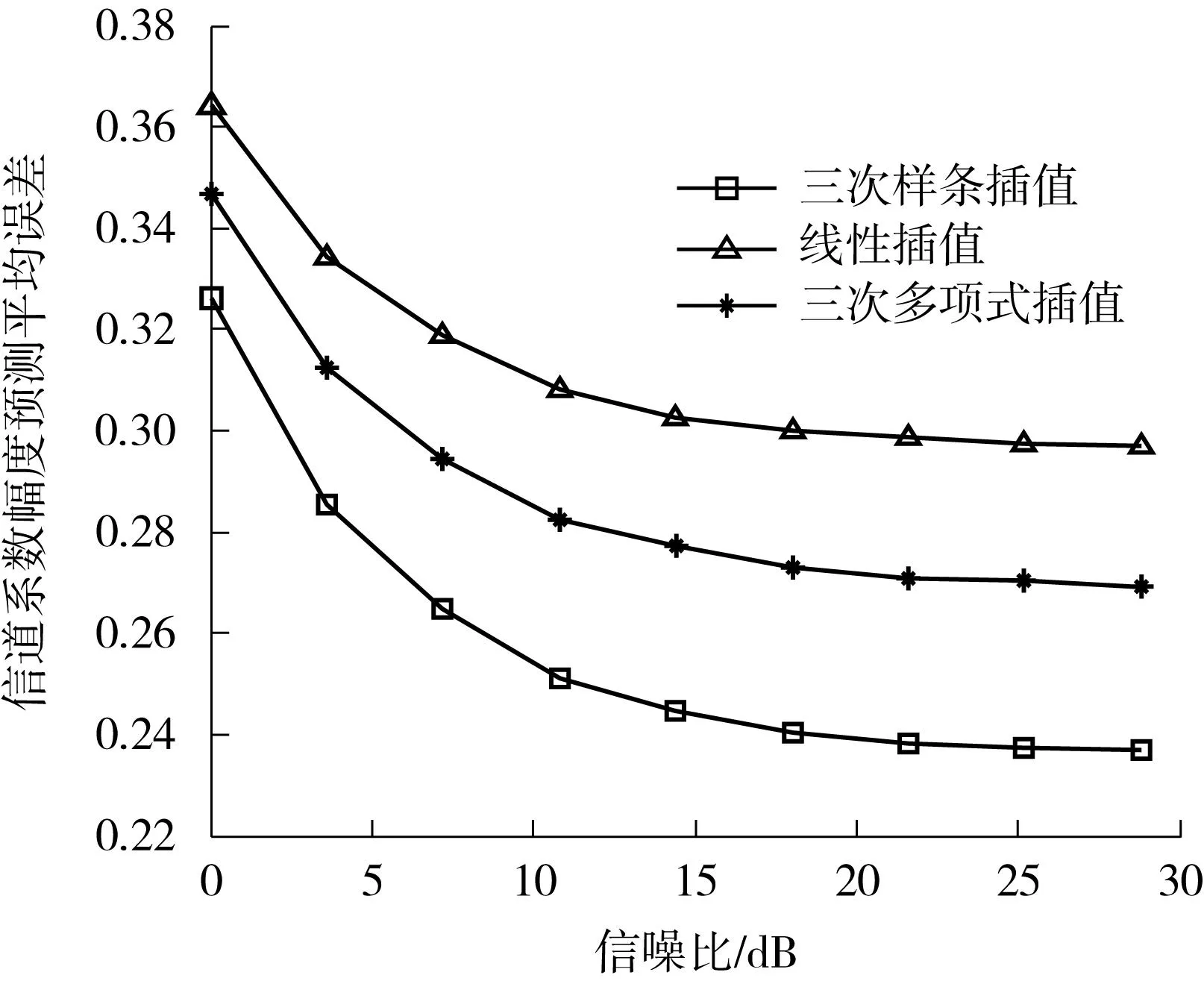
图3　3种插值算法预测平均误差比较 Fig.3　Comparison of prediction errors among three interpolation algorithms

如图3所示,三次样条插值法的精度优于另两种插值算法,这也是文中仿真实验选择三次样条插值法拟合数据传输速率上信道系数的原因.

5结语

文中研究了3种可用于信道预测中的基本算法,针对MEM方法计算量大、存在误差扩散及ESPRIT算法精度受制于自相关函数的估计问题,提出采用扩展Prony算法对平坦快衰落信道进行预测.扩展Prony算法适用于具有衰减震荡分量的非平稳过程的研究,该算法提取信号特征能力强,有很好的外推能力,具有一定的抑制噪声能力.预测信道系数时,直接利用采样数据,无需估计自相关函数,估计误差较小,可适应信道模型； 此外，做短距离预测时计算量不大.充分利用模型特点,求取快衰落过程中的短时不变量,可以实现一定时间范围内的批量处理、多步预测.理论分析和仿真结果表明,扩展Prony算法比MEM方法及ESPRIT算法稳定，精确度高.

参考文献：

[1]SiJiangbo,HuangHaiyan,LiZan,etal.Performanceanalysisofadaptivemodulationincognitiverelaynetworkwithcooperativespectrumsensing[J].IEEETransactionsonCommunications,2014,62(7):2198-2211.

[2]GuoShuxia,SongYang,GaoYing,etal.lowcomplexityminimummeansquareerrorchannelestimationforadaptivecodingandmodulationsystems[J].ChinaCommunications, 2014,11(1):126-137.

[3]HuanZhang,PathiranaPN.uplinkpowercontrolviaadaptivehidden-Markov-model-basedpathlossestimation[J].IEEETransactionsonMobileComputing,2013,12(4):657-665.

[4]EyceäzT,Duel-HallenA，HallenH.Predictionoffastfadingparametersbyresolvingtheinterferencepattern[C]∥Proceedingsofthe31stASLOMARConferenceonSignals,SystemsandComputers.PacificGrove:IEEE,1997:167-171.

[5]JφrgenBachAndersen,JesperJensen,SφenHoldtJen-sen,etal.Predictionoffuturefadingbasedonpastmea-surements[C]∥ProceedingsofIEEEVTS50thVehicularTechnologyConference.Amsterdam:IEEE,1999:151-155.

[6]TaoJia,Duel-HallenA,HallenH.Data-aidednoisereductionforlong-rangefadingpredictioninadaptivemodulationsystems[J].IEEETransactionsonVehicularTechnology,2013,62 (5):2358-2362.

[7]BergerCR,ZhouShengli,PreisigJC,etal.Sparsechannelestimationformulticarrierunderwateracousticcommunication:fromsubspacemethodstocompressedsen-sing[J].IEEETransactionsonSignalProcessing,2014,58(3):1708-1721.

[8]KomninakisC,FragouliC,SayedAH,etal.Multi-inputmulti-outputfadingchanneltrackingandequalizationusingKalmanestimation[J].IEEESignalProcessingSociety,2002,50(5):1065-1076.

[9]PavlenkoVD,SperanskyyVO,LomovoyVI.Modelingofradio-frequencycommunicationchannelsusingVolterramodel[C]∥Proceedingsofthe6thIEEEIntelligentDataAcquisitionandAdvancedComputingSystems.Prague:IEEE,2011:574-579.

[10]TianbenDing,AkiraHirose.Fadingchannelpredictionbasedoncomplex-valuedneuralnetworksinfrequencydomain[C]∥Proceedingsofthe2013InternationalSymposiumonElectromagneticTheory.Tokyo:IEICE,2013:640-643.

[11]ProakisJG，SalehiMasoud.Digitalcommunications[M].5thed.NewYork:McGraw-Hill,2007:839-843.JG，SalehiMasoud.Digitalcommunications[M].5thed.NewYork:McGraw-Hill,2007:839-843.

[12]EyceozT,Duel-HallenA,HallenH.Deterministicchannelmodelingandlongrangepredictionoffastfadingmobileradiochannels[J].IEEECommunicationsLetters,1998,2(9):254-256.T,Duel-HallenA,HallenH.Deterministicchannelmodelingandlongrangepredictionoffastfadingmobileradiochannels[J].IEEECommunicationsLetters,1998,2(9):254-256.

[13]BurgJP.Maximumentropyspectralanalysis[C]∥Proceedingsof37thAnnualInternationalMeetingofSocietyofExplorationGeophysics.Oklahom:[s.n.],1967.JP.Maximumentropyspectralanalysis[C]∥Proceedingsof37thAnnualInternationalMeetingofSocietyofExplorationGeophysics.Oklahom:[s.n.],1967.

[14]ProakisJG,ManolakisDimitrisG.Digitalsignalprocessing[M].3rded.NewJersey:PrenticeHall,1996:925-929.

[15]RappaportTS.Wirelesscommunications[M].2thed.NewJersey:PrenticeHall,2002:177-181.

[16]SpillardC,PoveyGJR.ApplicationofthePronyalgorithmtoapredictiveRAKEreceiver[C]∥ProceedingsofIEEE4thInternationalSymposiumSpreadSpectrumTechnologyandApplications.Mainz:IEEE,1996:1039-1042.C,PoveyGJR.ApplicationofthePronyalgorithmtoapredictiveRAKEreceiver[C]∥ProceedingsofIEEE4thInternationalSymposiumSpreadSpectrumTechnologyandApplications.Mainz:IEEE,1996:1039-1042.

[17]张贤达.现代信号处理[M].2版.北京:清华大学出版社,2002:119-125.

FlatFast-FadingChannelPredictionAlgorithmontheBasisof

ExtendedPronyAlgorithm

Zhong Wei-zhiZhong Dan-danJing Qing-fengLiu Xin

(CollegeofAstronautics,NanjingUniversityofAeronauticsandAstronautics,Nanjing210006,Jiangsu,China)

Abstract：In order to overcome the high iteration load and error diffusion existing in maximum entropy method (MEM) and to improve the prediction accuracy of ESPRIT algorithm subjected to autocorrelation function estimation, a flat fast-fading channel prediction algorithm on the basis of extended Prony algorithm is proposed. By means of extended Prony algorithm, complex roots can be obtained via least square fitting and higher algebraic equations without estimating autocorrelation function, batch computation becomes possible, and thus both the prediction accuracy and the computation efficiency improve. Theoretical and simulated results show that, in comparison with MEM and ESPRIT algorithms, extended Prony algorithm provides higher prediction accuracy, 3～5 dB advantages at the same prediction accuracy, more steady performance and higher operation efficiency.

Keywords:fadingchannel;prediction;MEMalgorithm;ESPRITalgorithm;extendedPronyalgorithm

Foundationitems:SupportedbytheNationalNaturalScienceFoundationofChina(NSFC)(61072067, 61372076),theProgramofIntroducingTalentsofDisciplinetoUniversities(B08038)andtheSpecialFoundationoftheStateKeyLaboratoryofIntegratedServicesNetworks(ISN1001004)