基于有向图的刀轴矢量优化研究

基于有向图的刀轴矢量优化研究

刘红军1曹宁江1赵吉宾2

1.沈阳航空航天大学，沈阳，1101362.中国科学院沈阳自动化研究所，沈阳，110016

摘要：针对球头铣刀的五轴数控加工，提出了一种基于有向图的刀轴矢量优化方法。根据刀轴矢量数据量大的特点，提出了建立刀轴矢量有向图的最小优化模型和算法。该方法能获得全局刀轴矢量变化量最小的刀轴矢量序列，将可行域边界上的刀轴矢量加入到有向图的计算中，提高了算法的计算效率。仿真分析表明，该方法优化了刀轴矢量的连续性和光顺性，对于最佳刀具姿态在可行域边界上的加工具有一定的适用性。

关键词：刀轴矢量；五轴数控加工；有向图；可行域边界；空间构造法

中图分类号：TP391.7

收稿日期：2014-07-28

基金项目：辽宁省自然科学基金资助项目(2013024017)

作者简介：刘红军，男，1971年生。沈阳航空航天大学机电工程学院副教授。主要研究方向为数控技术、数字化制造。发表论文25篇。曹宁江，男，1990年生。沈阳航空航天大学机电工程学院硕士研究生。赵吉宾，男，1970年生。中国科学院沈阳自动化研究所研究员。

Research on Tool Axis Vector Optimization Based on Graph

Liu Hongjun1Cao Ningjiang1Zhao Jibin2

1.Shenyang Aerospace University，Shenyang，110136

2.Shenyang Institute of Automation Chinese Academy of Sciences，Shenyang，110016

Abstract：According to the five axis NC machining of ball end milling, this paper presented a new method to optimize tool axis vector based on graph. Based on the characteristics of the cutter axis vector data, the minimum optimization model and algorithm of the cutter axis vector directed graph were proposed. This method can get global minimum cutter axis vector variation of cutter axis vector sequence and improve the computational efficiency of the algorithm by using the boundary of the feasible region of cutter axis vector joining in the directed graph calculation. Simulation and data analyses show that the proposed method improves the continuity and smoothness of cutter axis vector in a certain extent, and also has certain applicability in its optimal tool posture along the boundary of the feasible region.

Key words：tool axis vector; five-axis CNC machining; digraph; feasible domain boundary; space construction method

0引言

五轴数控加工是复杂零件高效加工的重要手段，使用非球头刀可以在避免干涉的同时通过调整刀具位置和姿态，使刀具包络曲面充分逼近理论设计曲面[1]。五轴数控加工中，刀具自由度的增加可以使刀具在一定范围内任意可控，提高了对于复杂曲面类零件加工成形的适应性。然而刀轴矢量的任意可控也给刀具轨迹规划带来了新的课题——刀具位姿规划。

刀具干涉处理是刀具位姿规划中需要首先考虑的问题。Lee等[2]应用曲面的凸包性质来解决复杂曲面五轴数控加工中的全局干涉问题；Lee等[3]基于距离计算提出了CA算法，用于解决刀轴矢量与被加工曲面和周围环境的干涉碰撞问题；Bi等[4]利用图形显卡中的遮挡查询功能快速检测干涉并且推广了可视锥法的应用。

刀轴矢量的连续性、光顺性是国内外的一个研究热点和难点。Ho等[5]通过降低加工中的非线性误差来得到较好的表面质量；Beudaert等[6]在机床坐标系下，通过光顺机床关节运动优化刀轴矢量；毕庆贞等[7]提出了一个类似于弹簧力学的整体网格优化模型，对相邻行刀轴矢量变化进行光顺处理。

构造空间法(C-空间法)[8]最初用来表示物体在三维空间中的自由度，就是将三维空间具有确定大小、形状的活动刚体转化为空间内的一个点，就等于将三维空间中的刚体运动降维到二维空间中的点移动，在很大程度上降低了研究刚体运动的复杂度。Jun等[9]将构造空间法引入到五轴数控编程的刀轴矢量规划中。本文基于构造空间法的基本思想，采用建立高斯球面映射的方法，在无干涉空间内直接规划出满足相关要求的刀轴矢量序列。

1点集可行域的建立

三维空间中，每一个刀触点处刀具位置的改变都可以看成是刀轴矢量的变化。为了降低优化的复杂度，根据构造空间的基本思想，将三维空间中的刀轴矢量转化成二维空间中的点。刀轴始终垂直于被加工曲面，因此可用被加工曲面上的点(α，β)表示工件坐标系下的刀轴矢量(i，j，k)。同时满足加工工艺约束和几何约束的点所形成的区域就是点集可行域。点集可行域中位于边界处的点就形成了可行域边界，如图1所示[5]。图1中，与黑色节点邻近的白色节点组成了刀轴矢量可行域的边界。可行域边界和边界内所有可行点构成了刀轴矢量可行域。

图1　刀轴矢量点集可行域

传统的可行域构造方法基于计算视觉中的边缘检测技术，通过这种检测技术获得满足加工工艺约束和几何约束的约束条件的刀轴矢量。这些刀轴矢量所构造的可行域空间和可行域边界就是图1中的白色区域。为了加快可行域边界的确定，通常将刀轴矢量的构造空间进行网格细分，每一个网格节点对应一个刀轴矢量数据。这样我们只需要对节点进行搜索，即可获得可行域边界。对于复杂曲面型腔类零件的五轴数控加工而言，最佳刀具姿态点通常位于可行域边界处。这是因为可行域的边界是由加工工艺约束和几何约束共同确定的，而可行域边界上的点是使刀具尽可能地贴合被加工曲面而不违反约束的极限位置。对于开阔曲面的加工而言，局部最佳刀具姿态通常是可行域边界上刀具倾角最小的点。

考虑刀轴矢量序列的光顺性和运动学性能时，局部最佳刀具姿态点就不一定是在可行域边界上了。为了获得整体最优的刀轴矢量序列，我们在选取最佳刀具姿态点时将考虑可行域内任意的可行点。刀具的矢量域范围为-90°～90°，本文将刀轴矢量域以每3°为网格的单位距离进行网格划分，以下简称3×3网格。取网格中每一节点的矢量构造刀具实体，通过干涉检测，并依据检测结果对所有刀轴矢量进行可行域和非可行域的归类处理。

2刀轴矢量变化量全局最小优化模型

工件坐标系下，刀触点轨迹上第i点的刀轴矢量为υi，因为|υi|=1，所以把矢量υi的起点平行地移到原点O后，υi的终点就是以O点为球心的单位球面上的点，我们把这种映射称为刀轴矢量的高斯球面映射。

如图2所示，设第i个刀触点处的刀轴矢量为υi，第i+1个刀触点处的刀轴矢量为υi+1，那么两个相邻刀触点之间的刀轴矢量变化量可以用刀轴矢量间的夹角表示：

θ(υi，υi+1)=arccos(υi·υi+1)

(1)

刀触点序列上整体刀轴矢量变化量之和可表示为

(2)

式中，n为刀触点总数。

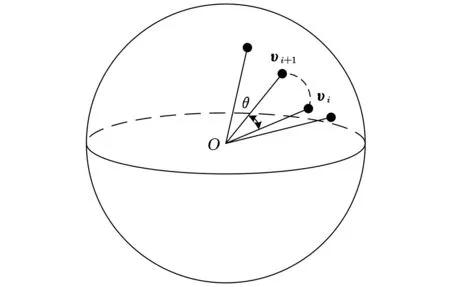
图2　刀轴矢量的高斯球面映射

因此，整体刀轴矢量的光顺性优化模型就可以转化为，以沿刀具进给方向刀轴矢量变化量最小为目标的优化模型：

(3)

其中，C为可行域中节点的集合。θmax为相邻刀轴矢量变化的阈值(根据进给速度和走刀步长共同计算获得)，反映在高斯球面上就是球面上两点的弧长，阈值越小，弧长越短，高斯球面上的离散点的分布就越密集。

3全局最小优化模型求解

对于点集可行域而言，每一个刀触点处都有一个刀轴矢量。相邻刀轴矢量可行域内，任意两个刀轴矢量都可以认为是相关的，都是可以存在于一个刀轴矢量序列内的。对刀轴矢量变化量全局最小优化模型(式(3))的求解可以简化为求从初始刀轴矢量到刀触点末端点处所有刀轴矢量的最短路径，该条路径上的这组刀轴矢量即为所求的最优的刀轴矢量。因此可以采用迪杰斯特拉算法进行求解。

前文将刀轴矢量域进行3×3的网格划分，某一刀触点处的刀轴矢量可行域最多可包含1800个矢量，而一个零件的刀具轨迹上往往需要几万甚至十几万个刀触点。由于顶点数极为巨大，因此，我们不但需要对顶点进行集域的划分，而且需要在求解的过程中对原有数据算法进行改进。加工时，走刀路径是没有重复的，这种情况下刀轴矢量就可以按照加工时刀触点的顺序建立刀轴矢量的有向图：假设每个可行刀轴矢量都是有向图中的一个顶点，且顶点i都唯一属于集合C(pi)。两个相邻集合内的顶点可以任意相关联，连接两顶点的连线称为弧。初始刀轴矢量或前一刀触点处的刀轴矢量称为弧头，后一刀触点处的刀轴矢量称为弧尾。将相邻刀轴矢量的变化量θ(υi，υi+1)设置为与弧相关的权。θ(υi，υi+1)超过相邻刀触点处刀轴矢量的最大变化阈值θmax时，将这条弧设置为无效并从有向图中剔除，从而建立带权有向图。建立有向图后，将初始刀轴矢量与刀触点轨迹末端点的每一刀轴矢量进行连通性检测。从初始点沿刀触点轨迹的进给方向向前逐一进行搜索，求出每一顶点到初始点的最小权值并记录；计算初始点到第二刀触点处所有可行刀轴矢量的权值，并记录；计算第三刀触点处每一刀轴矢量到初始点的最小权值，记录该权值和所对应的顶点路径；依次向前搜索直至轨迹末端。最后，比较末端每一路径的权值，找出对应的最短路径，以提高算法运行的效率。

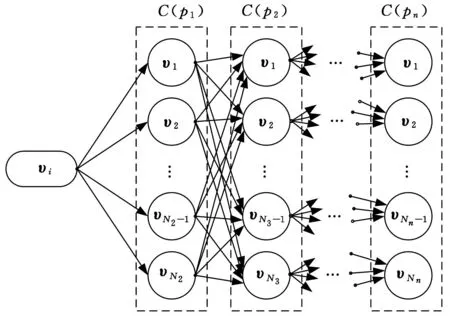
图3　点集域的刀轴矢量有向图(υ i为刀轴矢量)

4算例分析

算例1通过ACIS造型引擎建立工件几何模型，根据已知刀触点序列，构造直径为10mm的球头刀具模型；在每一刀触点处取该点刀具倾角α(0°≤α≤90°)、刀具摆角β(-90°≤β≤90°)的刀轴矢量变化区域，并以3×3进行网格划分。根据检测结果对网格节点上的刀轴矢量进行可行域划分，进而建立点集刀轴矢量可行域。最后通过第3节所提算法进行全局刀轴矢量计算。计算结果如图4所示，通过对机床各旋转轴的角度变化进行分析可以发现，我们所求的刀具加工路线的刀轴矢量变化最小，但刀轴矢量变化不均匀，刀轴矢量序列不平滑。

(a)3D仿真效果

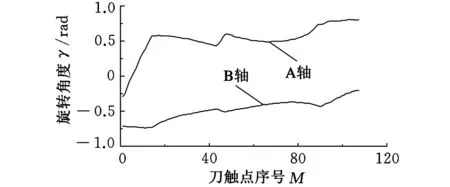
(b)旋转轴角度变化曲线 图4　3×3网格最短路径刀轴矢量优化

(a)3D仿真效果

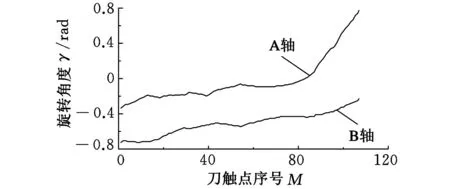
(b)旋转轴角度值 图5　网格最短路径刀轴矢量优化

算例2将算例1中3×3网格变为1×1网格，再进行计算。计算结果如图5所示，对比图4我们可以发现，各旋转轴角度变化明显均匀，但网格尺寸的减小极大地增加了刀轴矢量计算的时间。3×3网格划分进行计算所需要的计算时间为3294.21s。将3×3网格变为1×1网格再度进行计算，所需要的计算时间大大增加，为276 581.67s。

算例3从算例2中我们可以发现，可行域内存在大量对最终优化结果无实际影响的刀轴矢量，占用了大量的计算资源，因此算例3沿用算例2的网格划分尺寸，只提取出可行域边界上的刀轴矢量加入有向图，通过计算比较每一路径末端的权值来确定高斯球面上对应的最短路径，从而确定出光顺性最佳的路径。如图6所示，我们可以发现各旋转轴角度更为均匀，刀具路径更为光顺。另外，本次计算总耗时为546s，相对算例1和算例2的计算时间大为缩短。

(a)3D仿真效果

(b)旋转轴角度值 图6　可行域边界点集的最短路径刀轴矢量优化

5结语

基于空间构造法对刀具加工轨迹进行优化，在一定程度上解决了刀轴矢量不连续、不光顺的问题，同时得到了满足机床运动要求的刀具轨迹。对于最佳刀轴矢量位于可行域边界上的实例，本文算法可快速计算出刀轴矢量序列。

本方法仍存在一定的不足：刀轴矢量优化方法虽然能获得全局刀轴矢量变化量最小的刀轴矢量序列，但精度受网格尺寸的影响较大，网格划分越细，精度越高。

参考文献：

[1]盛耀元，郑刚，朱利民．UG二次开发在三阶切触加工刀位规划中的应用[J]．组合机床与自动化加工技术，2011，7(7)：12-15.

ShengYaoyuan，ZhengGang，ZhuLimin.UGSecondaryDevelopmentofToolPositioningforFive-axisMachiningUsingThird-orderPointContactApproach[J].ModularMachineTool&AutomaticManufacturingTechnique，2011，7(7)：12-15.

[2]LeeYuanShin，ChangTienChien. 2-PhaseApproachtoGlobalToolInterferenceAvoidancein5-axisMachining[J].Computer-AidedDesign，1995，27(10)：715-729.

[3]LeeLL，ZhangYF.CutterSelectionfor5-axisMillingofSculpturedSurfacesBasedonAccessibilityAnalysis[J].InternationalJournalofProductionResearch，2006，44(16)：3303-3323.

[4]BiQZ，WangYH，DingH.AGPU-basedAlgorithmforGeneratingCollision-freeandOrientation-smoothFive-axisFinishingToolPathsofaBall-endCutter[J].InternationalJournalofProductionResearch，2010，48(4)：1105-1124.

[5]HoMC，HwangYR，HuCH.Five-axisToolOrientationSmoothingUsingQuaternionInterpolationAlgorithm[J].InternationalJournalofMachineToolsandManufacture，2003，43(12)：1259-1267.

[6]BeudaertX，PechardPY，TournierC. 5-AxisToolPathSmoothingBasedonDriveConstraints[J].InternationalJournalofMachineToolsandManufacture，2011，51(12)：958-965.

[7]毕庆贞，王宇晗，朱利民，等. 刀触点网格上整体光顺五轴数控加工刀轴方向的模型与算法[J]. 中国科学：技术科学，2010，40(10)：1159-1168.

BiQingzhen，WangYuhan，ZhuLimin，etal.WhollySmoothingCutterOrientationsforFive-axisNCMachiningBasedonCutterContactPointMesh[J].ScienceChina：TechnologyScience，2010，40(10)：1159-1168.

[8]Lozano-PerezT.SpatialPlanning:aConfigurationSpaceApproach[J].IEEETransactionsonComputers，1983，32(2)：108-119

[9]JunCS，ChaK，LeeYS.OptimizingToolOrientationsfor5-axisMachiningbyConfiguration-spaceSearchMethod[J].Computer-AidedDesign，2003，35(6)：549-566.

(编辑张洋)