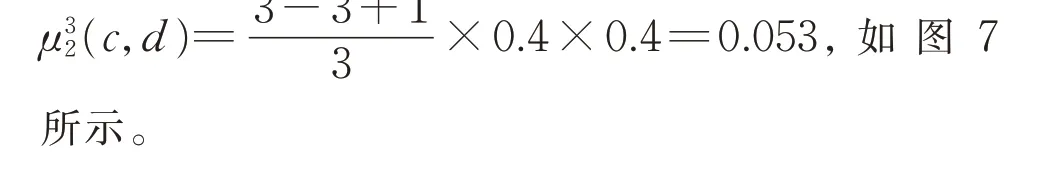m-步p-竞争模糊图

李瑞娟，韩晓影，张新鸿

（1. 山西大学 数学科学学院，山西 太原030006；2. 太原科技大学 应用数学系，山西 太原030024）

0 引言

本文中涉及的有向图是无环、无多重弧的简单有向图。

模糊集［3］是描述不清晰、不确定和界限模糊事物的一种重要数学结构。1987 年Bhattacharga 提出了模糊图［4］的概念。随后双极模糊图［5］、直觉模糊图［6］、模糊平面图［7］等概念被相继提出。将模糊图与竞争图的概念相结合，提出了双极模糊竞争图［8］、直觉模糊竞争图［9］、双极单值中智模糊竞争图［10］等概 念。2013 年，Samanta 和Pal 介 绍 了p-竞 争 模 糊图［11］。2015 年，Samanta、Akram 和Pal 介绍了m-步模糊竞争图［12］。

近年来，关于模糊图的最新结果，参看文献［14-16］。结合p-竞争模糊图和m-步模糊竞争图得到m-步p-竞争图在模糊图上的推广。

1 准备工作

定义3［3］集A={(X，σ)}称为集合X上的模糊集，其中σ：X→[0，1]。对于X中的一个元素x，σ(x)表示x的隶属函数。

两个模糊集A1= {(X，σ1)}，A2= {(X，σ2)}，则A1∩A2= {(X，min {σ1，σ2})}。

集A={(X，σ)}为集合X上的模糊集，若X0是由X中满足σ(x)≠0 的元素x所组成的集合，则称子集A0={(X0，σ)}为A的支撑集。|supp(A0)|表示集A0中元素的个数。

定义4［11］h(A)=max {σ(x)|x∈X}称 为 模糊集A={(X，σ)}的高度。

定 义5［4］设X是 一 个 非 空 集，映 射μ→：X×X→[0，1]称为X上的模糊关系。

在本文中用x∧y表示min {x，y}，用x∨y表示max {x，y}。

Rosenfeld 在1975 年提出了模糊无向图［17］的定义，将模糊无向图定义中的边改为弧，则得到下列模糊有向图的定义。

例1 图1 为一个模糊有向图D→。

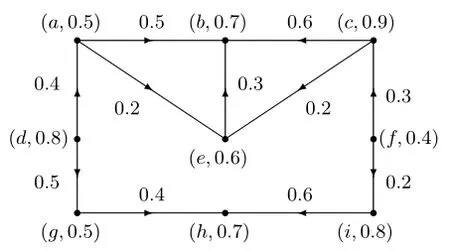
图1 模糊有向图D→Fig. 1 A fuzzy digraph D→

例2 图1 中各顶点的内邻集和外邻集分别如表1 和表2 所示。

表1 图1中各顶点的内邻集Table 1 In-neighbourhood of each vertex in Fig.1

表2 图1中各顶点的外邻集Table 2 Out-neighborhood of each vertex in Fig.1

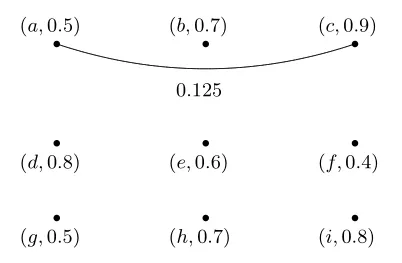
图2 2-竞争模糊图C2(D→)Fig. 2 The2-competition fuzzy graph C2(D→)

例5 图1 的2-步模糊有向图如图3 所示。

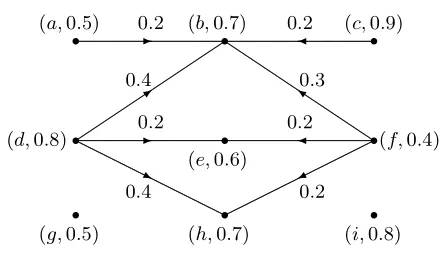
图3 2-步模糊有向图Fig. 3 2-step fuzzy digraph

图4 2-步模糊竞争图C2(D→)Fig. 4 2-step fuzzy competition graph C2(D→)

2 m-步p-竞争模糊图

图5 2-步2-竞争模糊图C22(D)Fig. 5 2-step 2-competition fuzzy graph C22(

因此边(x，y)是弱的。

3 应用

图6 模糊有向图D→Fig. 6 A fuzzy graph D→

图7 2-步3-竞争模糊图C32(D→)Fig. 7 2-step 3-competition fuzzy graph C32(D→)