电场活化聚合物驱动器动态机电耦合特性研究

电场活化聚合物驱动器动态机电耦合特性研究

陈娟刘焜

合肥工业大学，合肥，230009

摘要：通过分析电场活化聚合物材料的力学行为理论，建立了基于常见应变能函数(Mooney-Rivlin模型、Ogden模型和Yeoh模型)的电场活化聚合物驱动器的机电耦合本构模型。通过驱动实验，将3种机电耦合模型结果与实验数据进行了对比分析，得出影响电场活化聚合物机电稳定性的重要因素，确定了最适用于电场活化聚合物的机电耦合性能行为的模型。

关键词：电场活化聚合物; 本构关系; 机电耦合；驱动性能

中图分类号：TB381；TQ334

收稿日期：2015-01-16

基金项目：高等学校博士学科点专项科研基金资助项目(20120111110026)

作者简介：陈娟，女，1970年生。合肥工业大学机械与汽车学院博士研究生。主要研究方向为新型材料特性及应用。发表论文5篇。刘焜，男，1963年生。合肥工业大学机械与汽车学院教授、博士研究生导师。

Research on Dynamic Electromechanical Coupling

Characteristics of Dielectric Elastomer Actuator

Chen JuanLiu Kun

Hefei University of Technology，Hefei，230009

Abstract：The mechanical behavior theory of DE material was analyzed herein. The electromechanical coupling constitutive model of DE drive was built based on the common strain energy function, such as Mooney-Rivlin model, Ogden model, and Yeoh model. Through the drive experiments, the experimental data was compared with ones from three kinds of electromechanical coupling model. Then the important factors that affected the electromechanical stability of the DE were obtained, and the most suitable model of electromechanical coupling performance behavior used for DE material was determined.

Key words：dielectric elastomer(DE); constitutive relation; electromechanical coupling; driving performance

0引言

电场活化聚合物(dielectric elastomer，DE)是电活性聚合物中一类智能薄膜材料[1]。薄膜材料的力学性能是影响机电耦合致动性能的重要因素。DE薄膜材料具有高弹性能密度(3.4J/g)[2]，在外加电场下能产生较大的应变。当电场超过电场活化聚合物的临界点时，薄膜材料被击穿，导致电场活化聚合物驱动器机电耦合系统不稳定。为了研究其机电耦合系统稳定性，可以应用多个材料常数的弹性应变能函数模型对电场活化聚合物驱动器的机电稳定性进行分析[3]。但这些机电耦合研究，大多只是利用单一的应变能函数模型加以分析，并没有同时考虑多种应变能函数模型对机电耦合性能的影响。本文选用常用应变能函数模型(Mooney-Rivlin模型、Ogden模型和Yeoh模型)进行研究，构建三者应变能函数形式的机电耦合模型。通过平面机电驱动实验数据，将3种模型结果与实验数据进行对比分析，寻求影响电场活化聚合物机电稳定性的重要因素，从而确定最佳的机电耦合模型来指导电场活化聚合物器件的设计。

1DE驱动器机电耦合工作原理

材料的机电耦合特性的工作机理类似于一个电容器：中间层是DE薄膜材料，上下两层是屈从电极，如图1所示。当上下层电极通电后，DE薄膜材料处于电场中并产生形变，与此同时，涂敷在薄膜材料表面的电极材料也随电场的变化而变化，在上下薄膜表面上形成电场并保持其导电性。在电场的作用下，电极之间产生的有效压应力为

σz=εε0E2=εε0(U/d)2

(1)

式中，ε为绝缘常数；ε0为真空介电常数，ε0=8.85×10-12F/m；E为电场强度；U为施加电压；d为电力线方向的材料厚度。

(a)原始状态(b)通电状态 图1　电场活化聚合物驱动工作机理

根据电场活化聚合物材料自身所具有的超弹性力学特性，基于连续介质力学理论，假设薄膜材料在3个方向上的主延伸率为

(2)

式中，x、y、d分别为电场活化聚合物变形后的长度、宽度和厚度；x0、y0、d0分别为该材料变形前的长度、宽度和厚度。

根据假设条件，电场活化聚合物具有不可压缩性，则材料变形前后体积不变即xyd=x0y0d0。由于薄膜材料并不完全绝缘，在工作过程中存在一定量的传导电流，所以，在建立电场活化聚合物驱动器的电路模型中并联一个电阻，根据图2所示DE驱动器电路模型[4-5], 得到电路模型方程:

(3)

式中，Uc为薄膜材料两端电压；Re为电极电阻；te为电路的时间常数；c为薄膜电容。

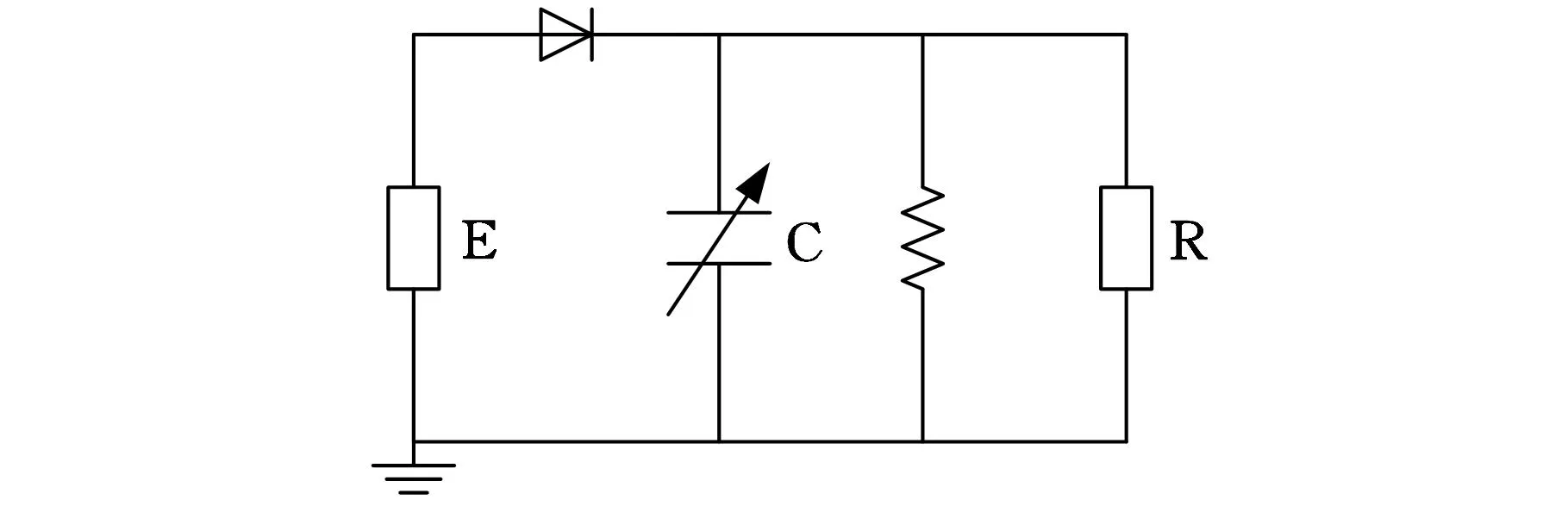
图2　DE驱动器电路模型

诸多实验表明，DE具有正-逆压电效应特性：在施加电场时产生伸缩变形，在施加压力时产生电压。因此，DE材料既可以作为致动器的基础材料，也可以作为传感器的基础材料。

2构建DE驱动器的机电耦合模型

2.1DE驱动器的本构关系

设预拉伸状态下的延伸率为λpi(i=1，2，3)，其中λp1=λp2=λp；材料通电状态下的延伸率为λi，材料预拉伸状态与通电状态的延伸率关系为

(4)

由式(2)、式(3)可得到预拉伸伸长比λ和k的函数方程：

(5)

当DE材料用于驱动器的设计时，工作频率不超过30Hz[6]。如果在同一个平面内材料沿着长度方向和宽度方向对薄膜材料进行双向拉伸，延伸率相等，即λ1=λ2，材料厚度方向上的应力σ3为零；如果在长度方向上进行拉伸，则其他两个方向延伸率相等，材料宽度方向和厚度方向上的应力σ2和σ3为零。根据超弹性材料的应变能函数，DE材料具备不可压缩特性，则材料的体积不变，即λ1λ2λ3=1。因此，主伸长比之间关系如下：

单轴拉伸

(6)

双轴拉伸

(7)

若是单轴拉伸，薄膜材料在平面内的名义应变可定义为

(8)

平面内Cauchy主应力张量σ1、σ2为材料的真实应力：

σ1=σ2=σp

(9)

(10)

式中，σp为预应力；p为静水压力；W为应变能。

所以，材料厚度方向上的Cauchy主应力为

(11)

Cauchy主应力相当于电极产生的静电压力：

σ=ε0εr(U/d)2=-σ3

(12)

式中，εr(λ1，λ2，λ3)为电活化状态后的相对介电常数。

厚度d0和厚度d的关系为

(13)

根据式(11)、式(12)和式(13)可得

(14)

从式(14)得出，DE大变形之后，其相对介电常数随着材料平面和厚度方向上的长度比呈线性变化[7-8]：

εr(λ1，λ2，λ3)=εi[1+A(λ3-1)+

B(λ1+λ2+λ3-3)]

(15)

式中，εi为初始相对介电常数，εi=4.7ε0；A、B为材料的电致伸缩系数。

为了得到精确的材料机电特性方程，将式(15)简化得到

εr(λ1，λ2)=εi[1+Q(λ1+λ2-2)]

(16)

式中，Q为电致伸缩系数，通常Q取-0.0053、0、1、2、-0.25。

根据式(14)、式(16)可得到电场活化聚合物的机电特性方程：

(17)

2.2DE驱动器的机电耦合模型

根据材料的本构理论，采用不同的应变能函数(Mooney-Rivlin模型、Ogden模型、Yeoh模型)分别与薄膜材料的电学模型相结合来建立DE驱动器的动态机电耦合模型[5]。

2.2.1Mooney-Rivlin形式

Mooney-Rivlin应变能方程[9-10]：

(18)

(19)

根据式(17)和式(19)可得

(20)

根据式(20)、式(4)、式(6)得

(21)

所以，根据式(3)、式(21)可得DE驱动器Mooney-Rivlin形式的机电耦合模型。

2.3Ogden形式

Ogden应变能方程为[11-13]

(22)

(23)

根据式(17)和式(23)可得

(24)

根据式(24)、式(4)、式(6)可得

(25)

所以，根据式(25)、式(3)可得到驱动器Ogden形式机电耦合模型。

2.4Yeoh形式

Yeoh应变能方程为[14-15]

(26)

(27)

根据式(17)和式(27)可得

(28)

根据式(28)、式(4)、式(6)得

[(C10+2C20D+3C20D2)+

(29)

根据式(29)、式(3)可得到驱动器Yeoh形式的机电耦合模型。

综上所述，机电耦合特性显现出材料驱动电压、薄膜表面延伸率λp与模型的材料参数之间的关系。因此，研究这3种因素对该材料的机电耦合性能的影响，对研究DE机电稳定性行为和设计制造驱动器件有着更深远的意义。

3试验和方法

为了深入研究电场活化聚合物机电稳定性，对薄膜材料进行机电耦合特性试验。

3.1试验过程

图3　试验平台

(a) 原始状态(b)预拉伸状态

(c)加电状态 图4　驱动试验过程

选取试件材料尺寸为φ30mm×10mm和30mm×30mm×1.1mm，预拉伸比分别取100%和200%，电极区域为φ19mm×0.45mm。在原有的拉伸试验装置中，增加了测试系统，如图3所示。对材料进行驱动试验：首先，进行预拉伸。预拉伸分为单轴预拉伸和双轴预拉伸，单轴预拉伸是指薄膜材料沿着一个方向(长度或半径)拉伸，双轴预拉伸指材料在互相垂直的两个直线方向上将薄膜拉伸。然后，在预拉伸的试件上加电施压。如图4所示，试验过程分别为3种状态：薄膜原始形状，薄膜预拉伸形状以及薄膜加电状态(薄膜是透明状，为了识别将材料中间涂抹黑色导电膏作为电极材料)。

3.2数据处理过程

整理应变能函数本构方程(Mooney-Rivlin模型、Ogden模型和Yeoh模型)拟合试验数据，选定了3种模型的材料参数(表1)。不同测试驱动电压下直径方向的变形和长度方向的变形如图5所示。利用MATLAB软件编写3种机电耦合模型的函数关系式，从而得到理论模型，如图6所示。

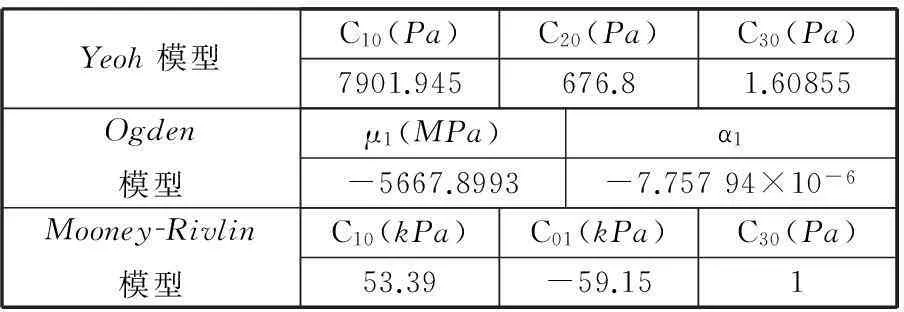
表1　本构模型参数

(a) 驱动电压-直径方向变形(圆形试件)

(b) 驱动电压-长度方向变形(矩形试件) 图5　驱动电压与直径(长度)形变量曲线

(a) 单轴拉伸

(b)双轴拉伸 图6　应力-延伸率关系曲线

从图5对比曲线看出，无论试件材料选取的是圆形还是矩形，同种预拉伸比下试验的结果大致相同，即随着预拉伸的增大，材料的变形率逐渐增大。当预拉伸比为100%时，圆形试件沿着直径方向产生5.8mm位移，需要的驱动电压为6255V；矩形试件表面在5889V驱动电压状态下，材料沿着长度方向(或宽度方向)产生的位移只有3.1mm；当预拉伸比为200%时，圆形材料沿着直径方向产生5.5mm的位移，需要的驱动电压为3590V，矩形材料沿着长度方向(或宽度方向)产生5.6mm位移，需要电压为3740V。这些数据充分表明，材料的变形量与预拉伸比有关，预拉伸比相同的情况下，圆形材料和矩形材料曲线略有不同，这是试验过程中人为操作误差所致，并不影响后续研究中将平面机电耦合模型与试验数据进行对比。

4试验结果及分析

4.1延伸率对驱动性能的影响

预拉伸的延伸率λ是衡量DE机电稳定性的重要参数，其对DE材料的驱动性能影响很大，根据DE材料平面机电耦合模型特性和麦克斯韦理论，随着延伸率增大，材料表面在电场作用下所产生的应力增大。通过DE力学模型的材料参数，得到材料驱动机电响应的3种模型拟合曲线，如图6所示。这3种模型曲线特征呈现出材料的非线性及驱动响应程度。

图6a中，3个模型的应力延伸率曲线相互接近，材料的非线性特征不是非常明显，Mooney-Rivlin模型曲线几乎呈现的是线性特性。这说明对材料进行单轴拉伸适合于小变形研究范围。

图6b中，薄膜材料的弹性模量很小，变形很大，如图所示，当延伸率λ2在2%以内时，Ogden模型和Yeoh模型比较接近；当λ2超过3%时，随着电压的增大，Ogden模型、Yeoh模型相距较远，应力增大趋势非常明显，两种模型曲线也不再有所交错，因此，Yeoh模型在大变形时的性能不如Ogden模型，这说明Ogden模型适合材料不同延伸率范围。但是，从Ogden模型拟合的曲线来看，由于本身的材料常数比较多，这里选择的是2个参数的Ogden模型，所以它能较精确说明材料非线性力学特性。Mooney-Rivlin模型趋于线性，应力增大趋于迟缓，不能反映材料的非线性程度。

4.2材料参数对驱动性能的影响

根据机电耦合特性试验数据结果，结合DE本构模型的材料参数，将平面驱动试验数据与应变能机电耦合模型数据进行对比，如图7所示。

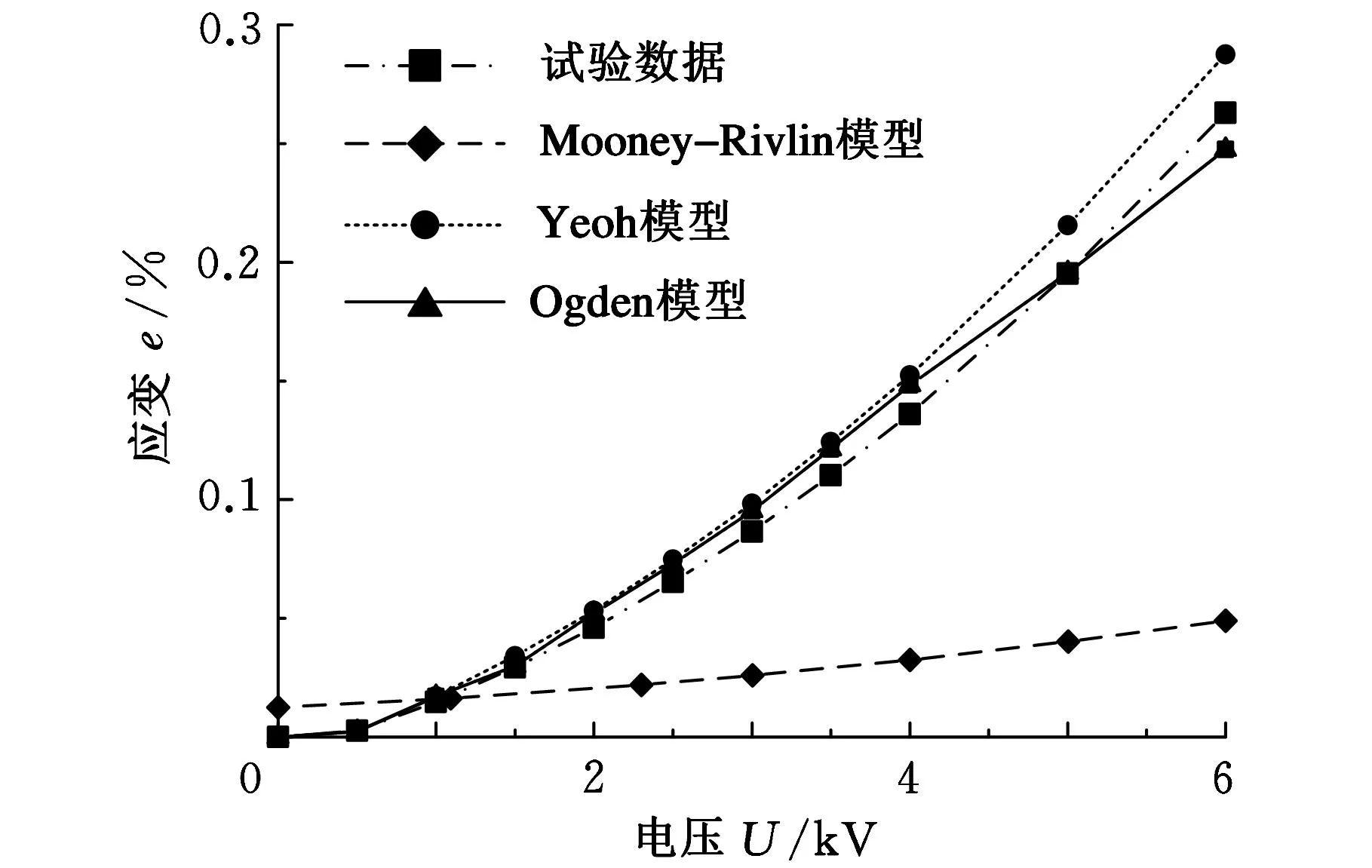
(a)电压-变形率(预拉伸比为100%)

(b)电压-变形率(预拉伸比为200%) 图7　平面驱动模型和试验数据曲线

分析图7可以看出：

(1)材料预拉伸比为100%时，随着施加电压的增大，3种机电模型驱动响应趋势都有增强，其中，Ogden模型曲线和试验曲线相吻合；Yeoh模型相比Ogden模型实验数据略有偏离，但是偏离值不是很大。预拉伸比为200%时，Ogden模型与试验曲线吻合；Yeoh模型与Ogden模型模型曲线虽然偏离试验数据，但也能反映DE材料的机电响应变化规律。

(2)Mooney-Rivlin模型和试验数据相差很大，机电响应不明显，曲线显现出线性特性，这与实际情况需要相差很大，在单轴和双轴预拉伸情况下，都不能作为后续器件设计与研究参考的依据。

(3)对比试验数据与模型可知，Ogden模型和Yeoh模型与试验数据比较接近，它们能充分反映DE材料的平面机电驱动特性，并且Ogden模型比Yeoh模型更适用于平面机电驱动响应研究。

5结语

根据材料的超弹性理论， 建立了电场活化聚合物驱动器为不同应变能函数时的机电耦合模型，描述了电场活化聚合物的机电耦合性能行为。试验数据对比表明，材料外加电压、弹性体薄膜的延伸率与电场活化聚合物模型的材料参数对电场活化聚合物机电耦合特性有影响。这验证了应变能模型材料参数结论。

参考文献：

[1]PerlineR，KohrnbluhR，PeiQ，etal.High-speedElectricallyActuatedElastomerswithStrainGreaterthan100%[J].Science, 2000, 287(5454): 836-839.

[2]盛俊杰，陈花玲，强俊花. 介电弹性材料的机电耦合性能研究[J]. 应用力学学报，2012，29(1)：38-40.

ShengJuanjie，ChenHualing，QiangJunhua.ResearchonElectromechanicalCouplingPropertiesinDielectricElastomers[J].ChineseJournalofAppliedMechanics，2012，29(1)：38-40.

[3]杨位东，王化明，魏礼建，等. 介电型EAP卷绕式驱动器的实现与应用[J]. 机械制造与自动化，2015，44(1)：163-167.

YangWeidong，WangHuaming，WeiLijian，etal.ImplementationandApplicationofDielectricElectroactivePolymerRollActuators[J].MachineBuilding&Automation，2015，44(1):163-167.

[4]林桂娟， 张欣波，王克胜.电活性聚合物发电实验[J].厦门理工学院学报，2013，21(3):45-49.

LinGuijuan，ZhangXinbo，WangKesheng.ExperimentationonEnergyConversionoftheDielectricElectroActivePolymer[J].JournalofXiamenUniversityofTechnology，2013，21(3):45-49.

[5]傅丹丹．基于EAP致动器的动态控制建模的基础研究[D]．杭州：杭州电子科技大学，2014.

[6]WisslerM，MazzaE.ElectromechanicalCouplinginDielectricElastomerActuators[J].SensorsandActuatorsA：Physical，2007，138(2): 384-393.

[7]SuoZ，ZhaoX，GreeneWH.ANonlinearFieldTheoryofDEFormableDielectrics[J].JournaloftheMechanicsandPhysicsofSolids，2008，56(2)：467-486.

[8]刘立武，孙寿华，刘彦菊，等. 具有线性介电常数的Ogden型介电弹性体的本构关系和机电稳定性[J]. 固体力学学报，2010，31(2)：181-192.

Liuliwu，SunShouhua，LiuYanju.ConstitutiveRelationElectromechanicalStabilityAnalysisofOgdenTypeDielectricElastomerwithLinearPermitivity[J].ChineseJournalofSolidMechanics，2010，31(2)：181-192.

[9]LiXF，YangXY.AReviewofElasticConstitutiveModelforRubberMaterials[J].ChinaElastomerics，2005，15(1): 50-58.

[10]MooneyM.ATheoryofLargeElasticDeformation[J].JournalofAppliedPhysics，1940，11: 582-592.

[11]DorfmannA，AustriaV，OgdenRW.NonlinearElectroelasticity[J].ActaMechanica，2005，174： 167-183.

[12]OgdenRW.LargeDEFormationIsotropicElasticity:ontheCorrelationofTheoryandExperimentofCompressibleRubberlikeSolids[J].ProceedingsoftheRoyalSocietyofLondon, 1972，A328：567-583.

[13]OgdenRW.OntheThermoelasticModelingofRubberlikeSolids[J].JournalofThermalStresses，1992，15：533-557.

[14]YeohOH.CharacterizationofElasticPropertiesofCarbon-black-filledRubberVulcanizates[J].RubberChemistryandTechnology，1990，63: 792-805.

[15]YeohOH.OntheOgdenStrainEnergyFunction[J].RubberChemistryandTechnology，1997，70：175-182.

(编辑张洋)