轻轨锚固螺杆单位脉冲响应信号的稀疏径向基函数网络提取

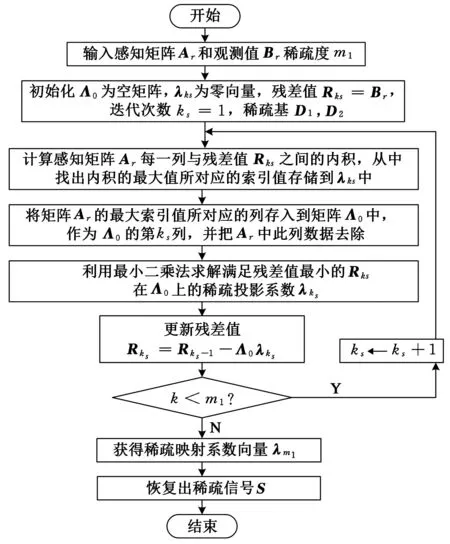
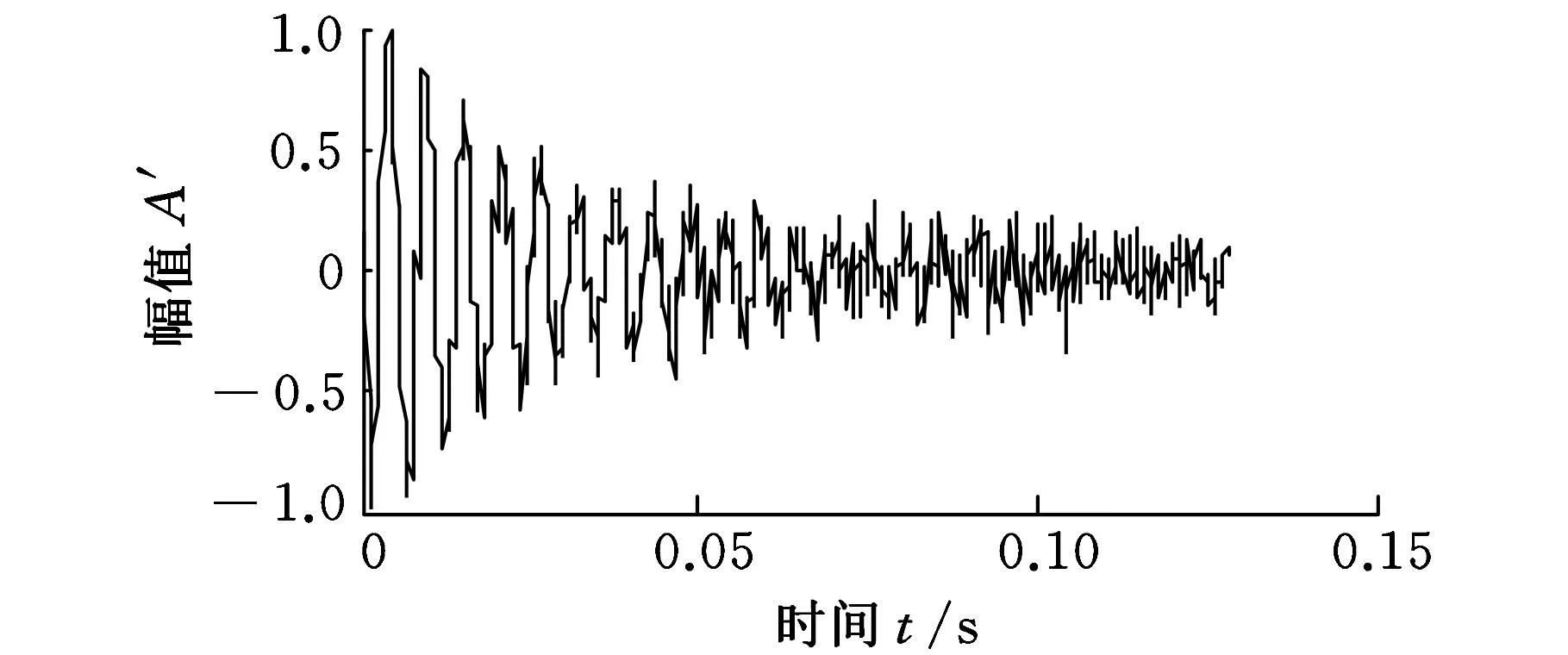
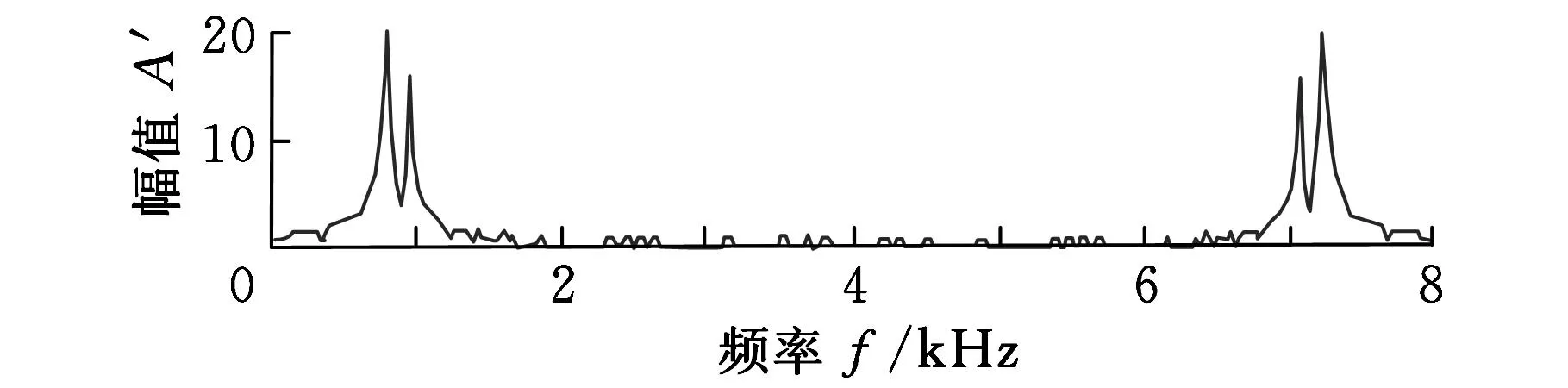
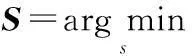轻轨锚固螺杆单位脉冲响应信号的稀疏径向基函数网络提取

杨丹周宇叶庆卫王晓东

宁波大学，宁波，315211

摘要：轻轨锚固螺杆是轻轨交通中连接轨道梁和墩台的关键受力部件，脉冲响应函数的提取是其健康监测的关键和核心技术。引入稀疏优化算法取代经典径向基网络的最小二乘法，构建网络的输入输出方案，引入二维DCT基对学习权值矩阵进行稀疏表示并通过正交匹配追踪算法来获得尽可能稀疏的网络训练权值。将单位脉冲激励信号输入该网络即可获得系统的单位脉冲响应函数。实验结果表明，所构建的稀疏径向基网络能准确提取单位脉冲响应函数，对工程应用具有参考价值。

关键词：径向基函数(RBF)网络； 轻轨锚固螺杆；正交匹配追踪算法； 脉冲响应函数

中图分类号：TP391.4

收稿日期：2015-04-27

基金项目：国家自然科学基金资助项目(61071198)；浙江省自然科学基金资助项目(LY13F010015)；宁波市自然科学基金资助项目(2012A610019)

作者简介：杨丹，女，1990年生。宁波大学信息科学与工程学院硕士研究生。主要研究方向为振动信号处理。周宇，男，1962年生。宁波大学信息科学与工程学院教授。叶庆卫，男，1970年生。宁波大学信息科学与工程学院副教授。王晓东，男，1969年生。宁波大学信息科学与工程学院副教授。

Extraction of Unit Pulse Response Function Based on Sparse RBF

Network Applyed in Rail Anchor Screw

Yang DanZhou YuYe QingweiWang Xiaodong

Ningbo University,Ningbo,Zhejiang,315211

Abstract:Light rail anchoring screw is a key force component for connecting rail girder and piers.The extraction of the impulse response function is the key premise and the core technology to the screw anchor’s health monitoring.Sparse optimization solution was introduced to replace the RBF network’s classical least square method.The sparse RBF network with input and output calculation scheme was constructed.Two-dimensional DCT-basis was introduced to represent the weight and the orthogonal matching pursuit(OMP) algorithm was used to get sparser network weights training value.A unit excitation signal was taken as the network’s input and the output of the network was the unit impulse response function of the system.The experiments show that optimization solution of the RBF network in the paper can accurately extract the impulse response function.The work herein has reference value in engineering applications.

Key words: radial basis function(RBF) network;light rail anchor screw;orthogonal matching pursuit(OMP) algorithm; impulse response function

0引言

轻轨交通系统是一种现代化水平高、主要面向旅客运输的中等客运量城市公交系统，而锚固螺杆是连接轨道梁和墩台的关键受力部件，若其出现松动、断裂等现象，将严重威胁轻轨列车的运行安全。因此对轻轨在役锚固螺杆进行健康监测具有重要意义[1]。利用结构的动态响应识别结构损伤是近年发展起来的结构损伤诊断新方法，其中模态参数是决定结构动力特性的主要参数，而单位脉冲响应函数的提取是振动信号模态分析理论的重要组成部分，许多算法(如SSI、ERA、ITD等)都是以单位脉冲响应函数为基础进行模态参数提取[2-3]。目前国内外对振动信号单位脉冲响应函数的提取方法有：基于FFT的功率谱法，直接求得频响函数；基于Duhamal积分的时域法，直接获得系统的单位脉冲响应函数；小波变换法，试图克服FFT功率谱法要求输入信号的频率成分丰富、只适用于稳态信号、存在能量泄露等固有的缺陷[4-5]来提取单位脉冲响应函数。而在实际应用中，常见的方法是NExt法、随机减量法等，但很多时候受环境影响信号中会夹杂着很多非线性噪声，这就使得NExt法、随机减量法等方法的应用受到一定限制，同时给识别精度带来影响。

文献[5]的径向基网络设计中先对网络输入层的输入样本矩阵采用LU变换，学习层的权值矩阵运用规则化最小二乘法来提取单位脉冲响应函数。本文在文献[5]的基础上提出对径向基网络学习层的权值矩阵用稀疏优化求解算法取代规则化最小二乘法。由于该权值矩阵不一定稀疏，本文先用二维DCT基对学习权值矩阵进行稀疏表示；其次通过稀疏优化的正交匹配追踪(orthogonal matching pursuit,OMP)算法来求解尽可能稀疏的网络权值矩阵，再通过稀疏反变换求解实际的学习权重；最后将单位激励脉冲信号输入此系统提取单位脉冲响应函数。

1稀疏径向基网络

RBF径向基神经网络[6]是一种性能优良的前馈型神经网络，它结构简单，只有一个隐层，具有全局的非线性逼近能力，可以以任意精度逼近任意的非线性函数，学习速度快，应用较为广泛。但是，对于非线性系统的建模,该神经网络的预测结果误差较大，而且抗噪性能较差。

1.1经典径向基及其权重学习

径向基函数神经网络首先要选择K个基函数，各基函数形式为φi(u-ci),i=1,2,…,K;j=1,2,…,N。由于距离是径向同性的，因此称为径向基函数。‖u-ci‖2表示差向量的模(即欧氏范数)。径向基神经网络的结构如图1所示。图中，u和Y分别为径向基网络的输入信号和输出信号， T为径向基网络的教师信号。径向基网络由三层即输入层、隐含层和输出层组成，其中输入层仅仅起到传输信号的作用，隐含层节点一般由高斯核函数作为径向基函数，输出层节点通常是简单的线性函数。

图1　径向基高斯函数的网络结构

基函数采用高斯函数[6]时，可表示为

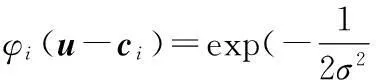
(1)

式中，ci为高斯函数的中心；σ为高斯函数的方差。

设计隐含层单元数为K,且K

即

(2)

满足

Y(u)=yj

记

yT=[y1y2…yN]

φT=[φ1(u-c1)φ2(u-c2)…φN(u-cK)]

WT=[w1w2…wK]

φij=φi(uj-ci)

则上述方程组可以改写成如下形式：

(3)

令φ表示元素为φij的K×N阶矩阵，W和Y分别表示权值向量和期望输出向量，上式可以写成：

Wφ=Y

(4)

显然φ是个对称矩阵，且与u的维度无关，当φ可逆时，可求得权值矩阵W，有：

W=Yφ-1

(5)

当输入的隐层神经元个数大于输入样本维数，且样本数目很大时，计算的权值矩阵会很大，容易产生病态问题，权值矩阵W的求解就不能用求逆W=Yφ-1，而用最小二乘法[7-8]求权值W：

W=Y×φT×(φ×φT)-1

(6)

另一种规则化最小二乘法的基本思想是通过加入一个含有解的先验知识的约束来控制映射函数的光滑性，使得相似的输入对应相似的输出，寻找逼近函数Y(u)通过最小化以下目标函数来实现：

(7)

式(7)中，第一项是均方误差，寻找最优的逼近函数，使均方误差最小，dj为Yj(u)的实际值，第二项用来控制逼近函数光滑程度，即为规则化项，λ是规则化参数，D是一个线性微分算子，代表了对Y(u)的先验知识，于是式(7)的解为

(8)

则权向量为

W=(φ+λI)-1d

(9)

径向基网络学习算法中用经典最小二乘法和规则化二乘法求解网络权值W时存在以下问题[8]：①在训练数据中存在较大噪声时，神经网络将拟合一个错误的曲面，从而使网络的泛化能力下降；②当输入样本数目过大时，权值矩阵成员值之间差距会很大，从而产生病态问题，可能就会导致求解不稳定。

为了提高网络的泛化能力，使得在有噪声的情况下也能较准确的提取脉冲函数，本文下面提出利用稀疏优化的OMP算法来获得稳定的网络权值W。

1.2径向基网络权重的稀疏求解算法

Donoho[9]指出，在某个基上具有稀疏描述信号的少量线性投影包含了重构和处理该信号的足够信息，也就是仅仅利用信号稀疏的先验和少量全局的线性测量就可以获得精确的重建。因此，对权系数W矩阵的重建过程可以看做是输出信号在径向基函数网络φ上的稀疏分解过程[10]。OMP算法[11-13]就是通过递归对已选择原子集合进行正交化以保证迭代的最优性，从而减少达到收敛的迭代次数。

径向基神经网络学习算法需要求解的参数有3个：基函数中心、方差和隐含层到输出层的权值。学习过程分为2个阶段：一是自组织学习阶段，此阶段为无导师学习过程，求解隐含层基函数的中心和方差；二是有导师学习阶段，这一阶段就是求隐含层到输出层之间的权值，本文利用稀疏优化的OMP算法求解权值矩阵W的最稀疏解,其步骤如下：

(10)

S就是W在二维DCT变换下的投影系数，由于一般矩阵在二维DCT变换下系数值集中在低频，一般来说S是稀疏[12]的。由此把问题从求解一般非稀疏的W变换成求解稀疏的S。

A×S=B

(11)

(3)构造随机观测矩阵G，对A和B随机采样，得到Ar=G×A，Br=G×B，式(11)表示为

Ar×S=Br

(12)

(4)令初始余量R0=Br,迭代次数ks=1,索引值集合Λ0=∅；

(5)计算相关系数，找到满足下述最优化问题的指标λks:

λks=arg max|Rks-1Arks|

(13)

(6)扩充指标集和矩阵，即令Λks=Λks-1∪{λks}，Arks←[Arks-1Arks],Ar0为空矩阵；

(7)解决如下最小乘问题：

(14)

(8)更新残差值：

Arks×S=BrksRks=Br-Brks

(9)ks←ks+1,若ks

(10)恢复信号S中的非零值指标为Λm1中的元素，第λj个元素的值等于Sks的第j个元素。

2基于稀疏径向基网络的单位脉冲响应函数提取算法

振动系统在单位脉冲激励信号作用下的自由响应称为单位脉冲响应函数，简称脉冲响应。在一个因果时不变线性系统中，系统的输出y(t)表示为脉冲响应函数h(t)与输入的卷积，写成积分形式为

(15)

简化整理为

Hu=Y

(16)

其中，H为系统的单位脉冲响应信号系数矩阵，u为输入信号组成的系数矩阵，Y为该因果时不变系统的响应信号矩阵。

从上式可以知道，用最小二乘法可以求脉冲响应信号H，当系统的输入信号存在较多的零值如脉冲信号等，求逆容易出现奇异矩阵，因此使用求伪逆的方法，但在噪声大的情况下，会使得最终提取的脉冲响应信号不可用。因此本文选择更加稳定可靠的算法来提取单位脉冲响应函数，构建稀疏径向基神经网络的输入输出方案，以及单位脉冲激励方案来提取脉冲响应信号。

已知输入信号矩阵u=[u1u2… uN],输出信号矩阵为Y=[y1y2… yN]，N代表样本输入信号数，每条样本信号的维数为m，第一条样本输入信号u1=[u11u12…u1m]，假设该径向基网络的输入信号矩阵u为N条轻轨锚固螺杆的采集信号，而输出信号Y是该输入信号矩阵u与理想单位脉冲信号h的卷积并加入白噪声得到的。

本文设计的稀疏径向基神经网络结构有3层[13-14]，输入层、隐层和输出层，输入的N条采集的信号矩阵u作为该径向基网络的输入，由理想的单位脉冲信号h和式(15)得到N条输出信号，将该输出信号加入信噪比RSN=5dB的白噪声Y作为该径向基网络的最终输出，即用这两个大量的信号矩阵对网络进行训练学习，其中用OMP算法得到隐层的权值矩阵W。这个网络就是一个已经训练好的神经网络，等同于一个物理系统。

训练完成后，采用单位脉冲激励方案，即取一条单位脉冲信号σ(t)输入到该训练好的网络中，那么该网络的输出就是系统对应的单位脉冲响应函数h(t)。具体过程如下：

(1)将采集的N条轻轨锚固螺杆的输入信号矩阵u输入到该网络中，由理想的单位脉冲信号h据下式可得到N条输出信号矩阵Y′:

Y′=u*h

(2)将得到的输出信号矩阵Y′添加RSN=5dB的白噪声后的Y作为网络的目的输出，输入信号矩阵u作为网络的输入，对该径向基网络进行训练学习，由最终输出为隐层节点输出的线性组合，已知输出信号矩阵Y和隐层输出的高斯函数φ，用稀疏优化的OMP算法可求得隐层的权值W：

(3)再取一条单位脉冲信号作为该网络的输入，那么最终网络的输出就是系统对应的理想的单位脉冲响应函数h(t)，即：

σ(t)*h(t)=h(t)

本文稀疏径向基网络提取单位脉冲响应函数的算法流程图和OMP算法流程图如图2所示。

(b)OMP算法 图2　算法流程图

3仿真与测试

3.1仿真理想脉冲响应函数时域分析

在MATLAB环境下进行仿真计算，每条信号的采样点数为1024，采样频率为8kHz，假设式(17)为仿真的理想单位脉冲信号h也就是教师信号：

h=0.9exp(-5t)cos(2π1300t+0.1)+

0.5exp(-3t)cos(2π1500t+0.05)

(17)

式(17)是双模态时不变因果线性系统。本文采用传感器采集到的轻轨锚固螺杆的激励信号作为输入信号uk，N为训练网络的样本数为72，径向基函数的隐层点数K=30。

由式(15)可以精确的计算系统的输出响应信号，然后把不同强度噪声信号与系统的激励信号和响应信号叠加，以输入信号矩阵和求解的加噪声的输出信号矩阵对径向基神经网络进行训练，理想的脉冲信号为教师信号，隐层径向基函数采用高斯径向基φ(u-ci)=exp(-λ‖u-ci‖2)，其中λ=1×10-5。

图3a和图3b是输入信号uk和该输入信号与仿真单位脉冲响应函数卷积的响应信号Yk,图3c是仿真的双模态理想单位脉冲响应信号h，图3d和图3e分别是本文算法获得的单位脉冲响应函数和经典径向基网络学习算法中的规则化最小二乘法提取的单位脉冲响应函数图形。本文仿真的脉冲响应信号h是双模态的，轻轨锚固螺杆的脉冲响应函数是显著双模态的，因此选用双模态信号[15]进行模拟仿真具有实际意义。

(a)输入信号(b)响应信号

(c)理想单位脉冲响应信号

(d)稀疏求解的单位脉冲响应函数

(e)规则化最小二乘法的单位脉冲响应函数 图3　两种算法提取的单位脉冲响应函数和 理想脉冲响应函数对比图

通过多次实验，结果显示径向基网络学习算法中的经典最小二乘法出现了很大的误差，提取不到单位脉冲响应函数。这是由于经典最小二乘法在求逆过程中出现了奇异矩阵，导致误差变大，所以在提取脉冲响应函数时经典最小二乘法不可行。通过图3d和图3e对比分析，利用提取到的单位脉冲响应函数与仿真理想信号的差值的均方根来计算误差，稀疏优化算法的误差是0.0290，而规则化最小二乘法的误差为0.0301，程序的运行时间是28.4283s。根据以上仿真验证稀疏优化的径向基网络提取单位脉冲响应函数算法是可行的，其中经典最小二乘法和规则化最小二乘法是经典径向基网络学习算法中的两种不同方法。

3.2仿真理想脉冲响应函数频域分析

在MATLAB环境下分别用本文提出的稀疏径向基网络算法获得的单位脉冲响应函数的频谱及规则化最小二乘法获得的单位脉冲响应函数的频谱如图4所示，采样频率是8kHz。图4a是仿真的理想脉冲响应函数实际频谱图，图4b是稀疏优化算法提取脉冲响应函数的频谱图，图4c是规则化最小二乘法提取脉冲响应函数的频谱图。经过10次仿真实验，规则化最小二乘法才能提取出如图4c所示的脉冲响应函数的两个显著模态频率，而稀疏优化算法更容易获得理想脉冲响应函数的两个显著模态，再次证明稀疏优化算法的优越性。

(a)理想单位脉冲函数频谱

(b)稀疏算法获得单位脉冲函数频谱

(c)规则化最小二乘法获得的单位脉冲函数频谱 图4　理想脉冲响应函数和两种算法的频谱图

4轻轨在役锚固螺杆的脉冲响应信号

本文研究对象是在役轻轨锚固螺杆[16]，因此选取一根长975mm，直径为36mm的不锈钢双头螺杆。锚固螺杆暴露在锚箱外的一端有一个用于在安装时定位的长度为25mm的扁方，在锚箱内的另一端则焊接了一个用于固定的球面螺母。通过传感器采集得到振动信号，分别采样获得一条激励信号uk和振动响应信号yk，其中采样频率为8kHz，每个信号的采样点数为1024，径向基函数神经网络的隐层节点数K=30，其锚固螺杆采集图如图5所示。

图5　测量转置示意图

图6是由传感器采集获得的一组实际激励信号uk和相应的振动响应信号yk，信号采样点数为1024。先将采集获得的多组激励信号和振动响应信号加噪后输入到网络进行训练，即可以获得脉冲响应函数。随后利用本文算法和规则化最小二乘法对单位脉冲信号进行测试，将单位激励脉冲信号输入到此训练好的网络中，得到网络输出即为轻轨锚固螺杆的单位脉冲响应函数。图7是稀疏径向基网络获得的轻轨锚固螺杆脉冲响应函数与经典径向基网络的规则化最小二乘法获得的轻轨锚固螺杆脉冲响应函数的时域图和频谱图。

(a)激励信号(b)响应信号 图6　激励信号和响应信号

(a)稀疏算法时域图(b)稀疏算法频域图

(c)规则化最小 (d)规则化最小 二乘法时域图 二乘法频域图 图7　稀疏算法与经典规则化最小二乘法的脉冲响应函数

从图7a和图7c的时域图对比可得，稀疏优化算法和规则化最小二乘法都能提取轻轨锚固螺杆的单位脉冲响应函数，且准确性较高。根据已知的锚固螺杆结构设计的物理参数，其在1000Hz、1300Hz、1500Hz和1800Hz附近都存在真实模态，具体的模态主频跟实际的锚固螺杆结构参数有关，并非确切的整数值。从理论值分析，稀疏优化算法得到的主频值更加精确，其它几个模态峰的结果也反映出稀疏优化算法得到的主频值更加接近理论值。从频谱图的对比可得，稀疏优化算法能获得轻轨锚固螺杆的脉冲响应函数1000Hz、1300Hz、1500Hz、1800Hz等多个显著模态；而规则化最小二乘法较难提取轻轨锚固螺杆的模态，经过8次实验才得到如图7d所示的频谱，且在1000Hz和1800Hz的模态峰值微弱，很不明显，容易造成频率泄漏。稀疏算法能提取频谱图中1000Hz处的模态峰，而规则化最小二乘法对1000Hz处的模态峰无法提取，会导致后期的模态参数识别有很大误差。因此，本文提出的稀疏径向基网络能更好提取锚固螺杆单位脉冲响应信号的显著模态，特别是较弱小的显著模态。

显著模态的提取直接影响单位脉冲响应函数中有效的模态参数的提取。对比发现，径向基函数神经网络的稀疏优化算法对提取实际信号的单位脉冲响应函数是可行的，并且效果较好；而使用经典最小二乘法提取轻轨锚固螺杆的脉冲响应函数时，由于求逆过程中奇异矩阵的出现，导致提取的脉冲响应函数误差极大，所以这一方法不可行。

损伤识别包含模态参数识别和损伤指标构造两个步骤，因此首先要获得结构的模态参数。获得锚固螺杆的单位脉冲响应函数后，利用随机子空间算法(SSI)提取其模态参数。将获得的模态参数输入到分类器中进行故障诊断。由于神经网络是非线性映射，所以在本文中，使用的训练样本都是通过真实锚固螺杆在有故障和无故障的情况下通过实验采集振动信号而来的，保证实验的可靠性。

5结论

综上所述，基于稀疏径向基网络RBF的单位脉冲响应函数提取算法具有可行性。相较于经典径向基函数神经网络学习算法的传统最小二乘和规则化最小二乘法，稀疏优化的OMP算法能够较好的提取单位脉冲响应函数，准确的获得脉冲响应函数的显著模态参数，而不用考虑最小二乘法中的奇异矩阵问题，可以应用于实际信号的脉冲响应函数提取。

参考文献：

[1]左鹤声, 彭玉莺. 振动实验模态分析[M]. 北京: 中国铁道出版社, 1995.

[2]林砺宗, 徐晓莉. 单位脉冲响应函数的测量技术[J]. 振动与冲击, 1994, 13(3): 56-60.

Lin Lizong，Xu Xiaoli.The Measurement Technology of Unit Impulse Response Function[J].Journal of Vibration and Shock,1994, 13(3): 56-60.

[3]陈恩伟, 刘正士, 王勇. 提取脉冲响应函数的小波变换法及时域法分析[J]. 振动工程学报, 2005, 18(2): 189-193.

Chen Enwei，Liu Zhengshi，Wang Yong.Wavelet Transform in Time Domain Method Analysis to Extract the Impulse Response Function[J].Journal of Vibration Engineering,2005,18(2):189-193.

[4]陈恩伟, 刘正士, 陆益民, 等. 一种提取系统脉冲响应函数的高效的去噪算法[J]. 振动工程学报, 2006, 18(4): 475-479.

Chen Enwei，Liu Zhengshi，Lu Yimin，et al. A Noising Algorithm of Extraction System Impulse Response Function with Efficient[J].Journal of Vibration Engineering,2006, 18(4): 475-479.

[5]周凯, 王晓东, 叶庆卫, 等. 基于神经网络解卷积的脉冲响应函数提取[J].中南大学学报(自然科学版)2011,42(S1): 67-71.

Zhou Kai， Wang Xiaodong,Ye Qingwei，et al.Extraction of Impulse Response Function Based on Deconvolution of Neural Network[J]. Journal of Central South University (Science and Technology), 2011,42(S1): 67-71.

[6]任远，白广忱. 径向基神经网络在近似建模中的应用研究[J].计算机应用，2009,29(1):115-118.

Ren Yuan，Bai Guangchen.Radial Basis Neural Network in the Application of Approximation Modeling Research[J]. Journal of Computer Applications, 2009,29(1):115-118.

[7]周伟. 基于非负矩阵稀疏分解和径向基神经网络的人脸识别方法[D]. 成都：电子科技大学, 2006.

[8]潘立登, 吴宁川. 径向基函数神经网络正交最小二乘改进算法的实现[J]. 北京化工大学学报, 2002, 29(4): 82-84.

Pan Lideng，Wu Ningchuan.RBF Neural Network Algorithm to Achieve Improved Orthogonal Least Squares[J].Beijing University of Chemical Technology,2002, 29(4): 82-84.

[9]Donoho D L.Compressed Sensing[J].IEEE Transaction Theory,2006,52(4):1289-1306.

[10]杨予昊, 陈卫东, 王东进. 基于 RBF 网络与 OMP 重构算法的空间自旋目标成像[J]. 中国科学技术大学学报, 2012, 41(11): 941-949.

Yang Yuhao，Chen Weidong，Wang Dongjin. Spatial Target Imaging Reconstruction Algorithm with OMP Based on RBF Network[J].University of Science and Technology of China.2012, 41(11): 941-949.

[11]Wu X, Deng W, Dong Y. A Weighted OMP Algorithm for Doppler Superresolution[C]//Antennas & Propagation (ISAP), 2013 Proceedings of the International Symposium on. IEEE, Dayton,2013: 1064-1067.

[12]韩红平. 压缩感知中信号重构算法的研究[D]. 南京：南京邮电大学, 2012.

[13]石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081.

Shi Guangming， Liu Danhua， Gao Dahua，et al.Compressed Sensing Theory and Its Research Progress[J].Journal of Electronics, 2009, 37(5): 1070-1081.

[14]Ye Qingwei，Sun Yang，Wang Xiaodong，et al. An Improved LLE Algorithm with Sparse Constraint[J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(12):2872-2876.

[15]王丹丹，周宇，叶庆卫. 基于谱聚类的振动多模态信号频谱分割研究与应用[J]. 中国机械工程，2013, 24(13):1719-1723.

Wang Dandan，Zhou Yu，Ye Qingwei. The Research and Application of Spectral Clustering Based on the Vibration Signal Spectrum Division Multimoda[J].China Mechanical Engineering,2013, 24(13):1719-1723.

[16]王琦, 汪同庆, 叶庆卫. 轻轨锚固螺杆振动信号EMD处理研究[J]. 振动与冲击, 2008, 27(6): 178-181.

Wang Qi，Wang Tongqing，Ye Qingwei.Ratment for Vibration Signal of Light-rail’s Screw with EMD[J].Journal of Vibration and Shock,2008, 27(6): 178-181.

(编辑王旻玥)