一种具有可拓展性解空间的平面杆组机构运动综合方法

一种具有可拓展性解空间的平面杆组机构运动综合方法

朱立红张良赵韩赵萍

合肥工业大学，合肥，230009

摘要：基于克利福德代数中的运动学映射理论，提出了一种新的具有可拓展性解空间的平面杆组机构运动综合方法。针对无精确解或数学意义上的最优近似解不能满足实际需求的情况，该方法可以根据需要来扩大拟合误差容许范围，进一步拓展解空间，从而获得更多近似解。之后，从中选取最优的二杆组来组成四杆机构或并联机构，实现给定的运动位姿。

关键词：机构运动综合；可拓展误差空间；平面杆组；运动学映射

中图分类号：TG156

收稿日期：2014-12-19

基金项目：国家自然科学基金资助项目(51405128)；中央高校基本科研业务费专项资金资助项目(2014HGCH0015)

作者简介：朱立红，女，1974年生。合肥工业大学机械与汽车工程学院讲师。主要研究方向为数字化设计技术、人机工程学。发表论文10余篇。张良，男，1973年生。合肥工业大学机械与汽车工程学院讲师。赵韩，男，1957年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。赵萍(通信作者)，女，1987年生。合肥工业大学机械与汽车工程学院副研究员。

A Novel Motion Synthesis Approach with Enlargeable Error Space Allowance for Planar Linkages

Zhu LihongZhang LiangZhao HanZhao Ping

Hefei University of Technology，Hefei，230009

Abstract：Using kinematic mapping theory in Clifford algebra, a new motion synthesis approach with enlargeable error space for planar linkages was proposed herein. This paper mainly focused on the situation when the given task yielded no exact solutions or the practical requirements that could not be realized by the mathematical optimal approximated solutions. By increasing error tolerance, the error space could be enlarged according to the requirements, thus more choices of approximated solutions could be introduced. After that, the optimal dyads may be selected to form a four-bar linkage or planar parallel linkages so as to realize the given task motion.

Key words：mechanism motion synthesis; enlargeable error space; planar linkage; kinematic mapping

0引言

平面杆件机构运动综合是根据给定位置、轨迹或函数来确定平面杆件机构的类型和尺寸。国内外学者在连杆机构的分析与综合理论研究方面已经取得了不少成果。Mruthyunjaya[1]对机构型综合方法进行了总结，给出了二副杆件的空间变换形式和三副杆件的不同几何构型，提出了用简单构件替代现有构件来降低机构复杂度的方法。Freudenstein等[2]采用图论研究平面机构的拓扑综合问题。Erdman等[3]针对平面四杆机构的闭环向量方程组的求解，给出了系统的方法。Bottema等[4]用运动学映射的方法来解决运动学问题。Su等[5]提出了基于曲线/曲面公式的方法，将机构综合问题转化为多项式系统的求解问题，并利用homotopy算法获取了最优解。黄茂林等[6]将机构分析过程与机构综合过程有机地结合起来，建立了四边形和五边形环路方程，给出了对应的求解方法，解决了平面高级机构函数发生器的综合问题。蓝兆辉等[7]提出了基于轨迹局部特性的机构轨迹精确实现方法，提高了轨迹机构求解精度和设计速度。王知行等[8]提出了基于计算机技术的平面四杆机构综合的数值比较法，提出了四杆机构的函数综合、轨迹综合和引导综合的转化方法，据此得到机构综合的基础解和优化后的满意解。周洪等[9]将机架方向结构误差的概念引入到曲柄摇杆机构的优化综合模型之中，解决了在生成曲线和理想曲线之间选择对应比较点的困难。褚金奎等[10]主要利用傅里叶变换的方法对机构进行轨迹与姿态的综合。黄真等[11]致力于研究基于螺旋理论的末端瞬时运动约束法，利用运动螺旋、约束螺旋、螺旋系统线性相关等概念来研究并联机构与空间机构的构型与尺度综合。文献[12-13]提出了平面曲线拟合的自适应方法，把机构综合问题转化为曲线自适应拟合问题，给出了平面近似圆点，建立了平面机构综合的模型和自适应方法，在理论上阐明了平面四杆机构运动综合问题存在最优近似解。Gao等[14]利用集合论方法，提出并联机器人末端特征的GF(generalized function) 集的概念和定义，创立了并联机器人机构的拓扑设计系统理论体系。戴建生等[15]将矩阵演算应用于变胞机构中描述其机构变化，预测机构的新构态。

根据经典Burmester理论，对于平面杆件机构运动综合，当给定连杆运动平面的2～5个位置时，可以精确求解；当给定连杆运动平面5个以上的位置，或要求连杆机构的运动符合某种连续平面运动函数，或要求运动平面中的点按某运动轨迹运动时，只能得到近似解。在当前的各种运动综合数学理论方法体系里，建立数学模型后，一般均可以得到数学意义上的最优解或精确解。但是很多情况下，这个数学意义上的最优解(具有最小的数学误差)不能满足实际要求，如铰链的位置不合适、某些杆件过长或过短等。针对上述问题，设计者需要拓展实际机构允许的误差空间，在更大误差的范围内寻找合适的拓展解来近似实现给定的运动。本文运用运动学映射的方法来解决这一机构综合难题。

1数学模型的建立

在基于运动学映射的平面刚体运动分析法中[4，16]，平面的刚体运动可以看成由刚体上的一个点(d1，d2)的平动和绕该点作旋转角度为φ的转动两部分组成。用M表示刚体上的某一点的运动姿态所确定运动坐标系Mxy，F表示刚体所在的固定坐标系OXY，如图1所示。则动坐标系与固定坐标系之间的关系为

[XY1]T=H[xy1]T

(1)

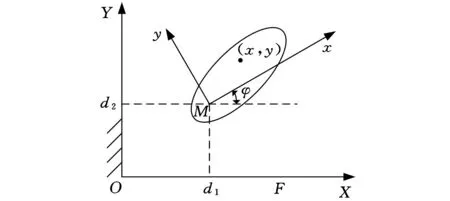
图1　平面刚体运动的坐标系

用Z=(Z1,Z2,Z3,Z4)来定义一个在四维空间中的点坐标，该四维空间被称为平面运动的映射空间。令

(2)

该映射将运动平面中的位姿转换为四维空间中的点。相应的，映射空间中的曲线可以表示单自由度运动，而曲面可以表示二自由度运动[17]。

2映射空间中的曲面拟合

我们在前期工作中发现，一个平面位姿如果可以由RR二杆组、PR二杆组或RP二杆组实现[17-18]，则该位姿转换成的映射空间点Z必然满足下列二次方程：

p3(Z2Z3+Z1Z4)+p4(Z1Z3+Z2Z4)+

p5(Z2Z3-Z1Z4)+p6Z3Z4+

(3)

该方程的参数pi(i=1，2，…，8)必须满足以下2个附加条件：

(4)

因此针对二杆组的运动综合问题可以转化为二次曲面的代数拟合问题，可以由一个过约束的线性方程组Ap=0来表示，即

(5)

(6)

该线性拟合问题包含2个二次约束条件，求解分为2个步骤：

步骤1：在最小二乘法意义上，针对N个线性方程拟合问题求取最优一般解空间，得到p，然后从一般解空间中寻找满足2个二次附加约束条件(式(4))的最优特定解。利用奇异值分解算法可以容易解决线性方程组的最小二乘法最优拟合问题。线性方程组Ap=0等价于pATAp=0，其过约束问题等价于求矩阵ATA的特征向量V。求出的8个特征向量对应的特征值可以反映各特征向量对应的最小二乘法拟合误差。设矩阵ATA相应排列的特征向量为v1，v2，…，也就是构成一般解空间的基向量。设α、β、γ、δ等为若干待定实系数，则一般解空间为

p=αv1+βv2+γv3+δv4+…

(7)

将8个特征值按照从小到大顺序排列，从小到大取出i(i=1,2,…,8)个特征值对应的i个特征向量，从而构成i维度的最优一般解空间。

步骤2：在最优解空间p中寻找能够满足式(4)的特定最优解。若要使齐次方程(式(4))有解，则p至少要包含3个待定系数，故所组成的最优一般解空间的维度至少为3，即

p=αv1+βv2+γv3

(8)

为了从该三维最优一般解空间中找到能满足式(4)的最优特定解，将p代入式(4)，得到关于(α，β，γ)的2个齐次方程：

(9)

其中，Kij由特征值分解算法得到的3个特征向量中的元素决定。这2个齐次三元二次方程可以整理为1个一元四次方程，继而直接根据求根公式求得解析解。因为该一元四次方程可能存在4个实根、2个实根或没有实根的情况，则系数向量p对应的可能有4个解、2个解或没有最优特定解。

此外，通过观察最优特定解p的情况，可以确定二杆组的运动副类型：①如果p1=p2=…=p5=0，系数向量p就代表PP型二杆组；②如果p1=p2=p3=0，系数向量p代表PR型二杆组；③如果p1=p4=p5=0，系数向量p代表RP型二杆组；④否则，系数向量p代表RR型二杆组。

针对最常见的RR、PR、RP平面二杆组，通过以上步骤确定了运动副类型之后，可以利用系数向量解p的8个元素(p1～p8)的具体数据来进一步确定二杆组的具体参数：

2.1RR型二杆组

RR型二杆组(图2a)表示的运动学约束为动坐标系中一个特定点(x，y)始终落在固定坐标系中的一个圆上，该圆的方程为

a0(X2+Y2)+2a1X+2a2Y+a3=0

(10)

利用所求得的系数向量p来确定该圆的方程，该圆的方程的系数关系可以表示为

a0∶a1∶a2∶a3=

(11)

动坐标系上这个特定点(x，y)也可以通过p求得：

(12)

2.2PR型二杆组

PR型二杆组(图2b)代表的约束是动坐标系中特定点(x，y)始终落在固定坐标系中一条直线上。由于直线与圆的耦合性，当p1=p2=p3=0即a0=0时，RR型二杆组的圆方程将降阶为直线方程：

2a1X+2a2Y+a3=0

(13)

因此PR型二杆组实际上是RR型二杆组的一种特殊形式。

2.3RP型二杆组

RP型二杆组(图2c)代表的约束为动坐标系中一条特定直线l1x+l2y+l3=0始终与固定坐标系中一个特定圆相切(等价于始终穿过固定坐标系中的一个特定点)，(l1，l2，l3)为动坐标系M上直线的齐次线坐标，该直线总是通过固定坐标系F上的特定点(-a1，-a2，a3)。

(a)RR二杆组　　　(b)PR二杆组(c)RP二杆组 图2　平面二杆组的类型

同样地，利用系数向量p来确定该动直线方程的系数(l1，l2，l3)与其穿过的点坐标(-a1，-a2，a3) 的系数之间的比值关系：

(14)

3平面杆组机构解空间的拓展

根据经典Burmester理论，求解通过某5个位姿的二杆组，理论上可以找到最多4个二杆组符合条件，即求出的二杆组都可以精确地通过该5个位姿，这些二杆组为精确解；当位姿数目超过5时，一般不存在精确解，只存在近似解。设计者可以通过数值方法找到若干个最优二杆组，使给定的位姿获得近似实现，这也是大多数现有的杆组机构运动综合理论的求解思路。但是这种求解思路可能存在许多问题：①在很多情况下，即使给定的位姿数目为5时也无法求出精确解，即不存在任何能够精确实现给定的5个位姿的二杆组；②在给定数学误差范围内(例如要求拟合误差小于0.005)，很多情况下设计者无法得到任何实数解；③在很多实际机构综合应用实例中，利用数学方法求得的具有“最小数学误差”的解其实并不能满足实际要求，如铰链的位置不合适、某些杆件过长或过短等。

以上这些机构运动综合过程中存在的问题都可能要求设计者在数学意义上“退而求其次”，降低对误差的数学要求，在更大误差的范围内寻找合适的“拓展解”，从而使得给定的位姿得到较好的实现。

为了实现对解空间的拓展，本文对线性方程组Ap=0的拟合问题进行了研究。由于矩阵ATA的8个特征向量对应的特征值可以反映各特征向量对应的拟合误差大小，所以若我们将特征值从大到小排列，并取最小的3个特征值对应的3个特征向量来构建“最优一般解空间”。之后，若将该特征向量代入式(4)无法求出实数解或所求的最优特定解不能满足实际要求时，设计者可以扩大误差容许范围，将第4个最小的特征值对应的特征向量也引入一般解空间，构建四维最优一般解空间，进一步求取能够满足条件的拓展解。

取方程的最小的4个特征值对应的4个特征向量vα、vβ、vγ和vδ构成解空间的基向量。设α、β、γ、δ为4个实参数，则解空间中任意向量可以表示为

p=αvα+βvβ+γvγ+δvδ

(15)

由于p必须满足2个附加条件(式(4))，将p代入式(4)，得到关于(α，β，γ，δ)的2个齐次二次方程：

(16)

其中，Kij由Zi(i=1，2，…，N)得到。因此，齐次参数(α，β，γ，δ)有无穷多个解可供选取。此时可以根据需要增加另外一个约束，例如给定RR型二杆组的固定铰链中心的位置或中心圆圆心(动铰链中心)的位置等[18]，来进一步确定有限数目的解。

4应用实例

为了进一步阐述本文提出的基于运动学映射的可拓展性运动综合方法，本节将通过应用实例来详细说明进行运动综合的过程与步骤。拟设计一个康复辅助机构，用于帮助人体完成由坐姿到立姿的动作，欲实现的运动姿态为正常人从坐姿到立姿过程中腰部运动轨迹的5个采样姿态，如图3所示，A、B为人体腰部的2个标记点。此 5个位姿在照片中测量的具体数据见表1，缩放比例为1∶5。这些数据来自于我们对不同体型正常人从坐姿到站立过程的多次重复采样建立的数据库。从数据库中选取与该病人体型最为接近的1组数据中的5个位姿，其中，(X，Y)为动坐标系原点位置，θ为动坐标系x轴与固定坐标系之间夹角。

图3　坐姿到站立过程中腰部运动 5个采样姿态(比例1∶5)

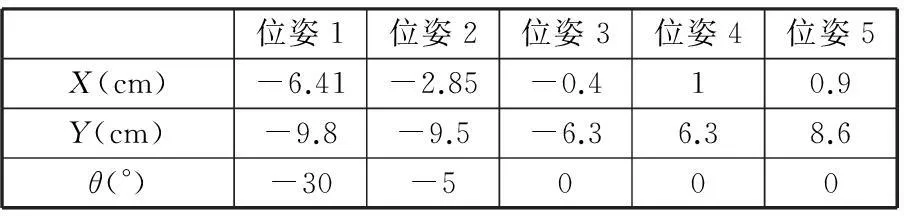
位姿1位姿2位姿3位姿4位姿5X(cm)-6.41-2.85-0.410.9Y(cm)-9.8-9.5-6.36.38.6θ(°)-30-5000

根据第3节所述流程，首先根据式(6)构建矩阵A，之后对矩阵进行奇异值分解变换。由前期工作[17-18]可知，对矩阵进行奇异值分解变换的过程即为对Ap=0进行最小二乘法拟合求解的过程。矩阵ATA有8个特征值，按照从大到小排序后，其中最小的3个特征值为0，如表2所示。

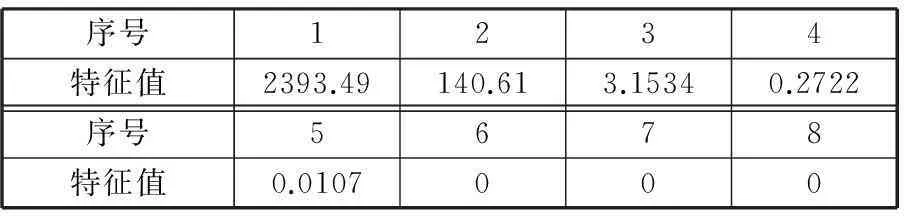
表2　矩阵A TA的8个特征值

由于至少需要3个特征向量才能保证式(3)有解，而特征值可以反映最小二乘法拟合误差，故理论上应取3个0特征值对应的特征向量来求解齐次三元二次方程组(式(9))，此时该齐次三元二次方程组有精确解，即所求得的机构可以精确实现要求的5个位姿，这与经典的Burmester理论相吻合。但二元二次方程组在一些情况下将会无实数解，即在一些情况下不存在任何能够精确实现给定5个位姿的二杆组。例如在上述康复辅助机构的实例中，利用包括Burmester理论在内的现有传统机构综合理论均无法找到精确通过5个采样位姿(表1)的二杆组。在此，我们利用本文提出的可拓展性运动综合理论，适度扩大误差空间，将最小的非零特征值0.0107所对应的特征向量也包含进来，在四维特征向量空间中求解能够实现给定位姿的二杆组。

4个特征向量对应特征值不全为0(最大的特征值为0.0107)，这说明在无法精确实现给定位姿的前提下，我们将拟合误差范围扩大至0.0107，在拓展后的误差空间内求取近似解。将此4个特征向量代入式(4)，得到1个三元二次方程组，该方程组存在无穷多解，利用文献[18]的方法，根据实际工作情况(康复机构所处的工作空间)添加一个额外约束条件：令固定铰链的位置在X=-6竖直线上，该竖直线为工作空间现有的固定机架。如此将求得3个二杆组解，见表3。综合考虑实际情况，我们选取第二组和第三组解，组成一个铰链曲柄摇杆机构，该机构的实际产生位姿轨迹与给定的5个位姿见图4，可以看出，即使在扩大拟合误差范围后，本方法求得的近似解依然可以较好地实现给定运动位姿。

表3扩展误差空间加入额外约束后的近似解

cm

5结语

本文提出了一种新的平面杆组机构运动综合方法，该方法可以根据实际需要对运动综合的最优一般解空间进行拓展。针对精确解不存在或数学意义上的有限最优解不能满足实际需求的情况，该方法通过引入更多特征向量，扩大拟合误差容许范围的方法来进一步拓展最优一般解空间，从而获得更多近似解。可以根据实际需要从中选取最优的二杆组来组成四杆机构或并联机构，使给定的运动位姿得到实现。最后借助一个五位姿运动综合的实例，阐述了当无法利用Burmester理论得到误差为0的精确解时，将数学误差范围扩大到0.0107，从而拓展了解空间，在0.0107的误差范围内求取到较为合适的二杆组解。本文所提方法可使机构运动综合理论在实际设计过程中得到更好的应用。

参考文献：

[1]Mruthyunjaya T S. Kinematic Structure of Mechanisms Revisited[J]. Mechanism and Machine Theory，2003， 38(4)：279-320．

[2]Freudenstein F，Dobrjanskyj L. On a Theory for the Type Synthesis of Mechanisms[A]//Applied Mechanics[M]. Berlin，Springer Heidelberg，1966：420-428．

[3]Erdman A G，Sandor G N. Mechanism Design：Analysis and Synthesis[M]. 3 ed. Upper Saddle River, N.J.： Prentice Hall，1997．

[4]Bottema O，Roth B. Theoretical Kinematics[M]. Amsterdam：North-Holland Pub. Co.，1979．

[5]Su H-J，McCarthy J M. Kinematic Synthesis of RPS Serial Chains[C]//ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference．Montreal, Quebec, Canada，2010：1041-1047．

[6]黄茂林，刘伟. 平面六杆高级机构高阶函数发生器的综合[J]. 机械工程学报，1990，26(5)：14-22．

Huang Maolin，Liu Wei. Optimum Synthesis of High Order Function Generators of the Planar Six Bar with High Class Mechanism[J]. Chinese Journal of Mechanical Engineering，1990，26(5)：14-22．

[7]蓝兆辉，邹慧君．基于轨迹局部特性的机构并行优化综合[J]．机械工程学报, 1999, 35(5):16-19．

Lan Zhaohui，Zou Huijun．Concurrent Optimum Synthesis of Path Generating Mechanisms Based on the Local Characteristics[J]. Chinese Journal of Mechanical Engineering，1999, 35(5):16-19．

[8]王知行，关立文，李建生．平面四杆机构综合数值比较法的研究[J]．机械工程学报，2000，36(2)：47-50．

Wang Zhixing，Guan Liwen，Li Jiansheng，et al. Study on Numerical Comparison Method for Planar Four-bar Linkage Synthesis[J]. Chinese Journal of Mechanical Engineering，2000，36(2)：47-50．

[9]周洪，邹慧君．基于机架杆方向结构误差优化综合曲柄摇杆连续轨迹生成机构[J]. 机械工程学报，2000，36 (5)： 42-45．

Zhou Hong，Zou Huijun. Optimal Synthesis of Crank-rocker Linkagese for Continuous Path Generation Using Orientational Structural Error of the Fixed Link[J]. Chinese Journal of Mechanical Engineering，2005，6 (5)：42-45．

[10]褚金奎，孙建伟．连杆机构尺度综合的谐波特征参数法[M]．北京：科学出版社，2010．

[11]黄真，赵永生，赵铁石．高等空间机构学[M]. 北京：高等教育出版社，2007．

[12]王德伦，王淑芬，李涛. 平面四杆机构近似运动综合的自适应方法[J]. 机械工程学报，2004，37(12)：21-26．

Wang Delun，Wang Shufen, Li Tao. New Approach Mechanisms Synthesis by Adaptive Saddle-fitting[J]. Chinese Journal of Mechanical Engineering，2004，37(12)：21-26．

[13]王淑芬. 机构运动综合的自适应理论与方法的研究[D]. 大连：大连理工大学，2006.

[14]Gao F，Li W，Zhao X，et al. New Kinematic Structures for 2-，3-，4-，and 5-DOF Parallel Manipulator Design[J]. Mechanism and Machine Theory，2006，37(11)：1395-1411．

[15]戴建生，丁希仑，王德伦. 一空间变胞机构的拓扑结构变换和对应的矩阵演算[J]. 机械工程学报，2005，41(8)：30-35．

Dai Jiansheng，Ding Xilun，Wang Delun. Topological Changes and the Corresponding Metrix Operations of a Spatial Metamorphic Mechanism[J]．Chinese Journal of Mechanical Engineering,2005，41(8)：30-35.

[16]Ge Q，Zhao P，Purwar A. Decomposition of Planar Burmester Problems Using Kinematic Mapping[J]. Mechanisms and Machine Science，2013，14：145-157.

[17]Ge Q J，Zhao P， Purwar A. A Novel Approach to Algebraic Fitting of a Pencil of Quadrics for Planar 4R Motion Synthesis[J]. J. Comput. & Infor. Sci. in Eng.，2012，12(4)：41-50．

[18]Zhao P，Purwar A，Ge Q J. On the Complete Synthesis of Finite Positions with Constraint Decomposition via Kinematic Mapping[C]//Proceedings of the 2014 ASME IDETC Conferences. Buffalo，NY，USA，2014：DETC2014-34216．

(编辑张洋)