变质量颗粒阻尼吸振器及其宽频减振性能

变质量颗粒阻尼吸振器及其宽频减振性能

赵艳青1夏晶晶1高强2宋伟志3韩宁2

1.淮阴工学院，淮安，2230032.长安大学，西安，7100643.洛阳理工学院，洛阳，471000

摘要：为了拓宽传统定参数颗粒阻尼吸振器的有效减振频带，设计了一种变质量颗粒阻尼吸振器。对变质量颗粒阻尼吸振器的动力学特性进行了仿真及实验研究，并利用数据拟合的方法建立了颗粒容器内水量与最佳减振频率的变化关系。研究结果表明：变质量颗粒阻尼吸振器可以通过改变颗粒容器内的液体量调节其最佳减振频率，拓宽了吸振器有效减振频带。

关键词：振动控制；动力吸振器；颗粒阻尼吸振器；变质量颗粒阻尼吸振器

中图分类号：TP273

收稿日期：2015-04-02

基金项目：国家自然科学基金资助项目(51175049，51275380)

作者简介：赵艳青，男，1985年生。淮阴工学院交通工程学院助教。主要研究方向为机械振动控制和非线性动力学数值计算。发表论文3篇。夏晶晶，男，1974年生。淮阴工学院交通工程学院教授。高强，男，1970年生。长安大学汽车学院教授。宋伟志，男，1987年生。洛阳理工学院机械系助教。韩宁，女，1990年生。长安大学汽车学院硕士研究生。

VMTPD and Its Performance of Wideband Vibration Reduction

Zhao Yanqing1Xia Jingjing1Gao Qiang2Song Weizhi3Han Ning2

1.Huaiyin Institute of Technology，Huaian，Jiangsu，223003

2.Chang’an University,Xi’an,710064

3.Luoyang Institute of Science and Technology，Luoyang，Henan，471000

Abstract:In order to extend the effective frequency band of a conventional TPD with fixed system parameters, a novel VMTPD was proposed herein. Dynamics properties of the new VMTPD were studied via simulations and experiments, and the relationship between the volume of water in container and the optimal frequency of vibration reduction was established by using data fitting method. The results show that the optimal frequency of vibration reduction of the proposed VMTPD can be adjusted by changing the volume of water, and a wideband VMTPD can be obtained.

Key words: vibration control; dynamics vibration absorber; tuned particle damper(TPD); variable mass tuned particle damper(VMTPD)

0引言

非阻塞性颗粒阻尼(non-obstructive particle damping, NOPD)技术由Panossian等[1-2]提出，并应用于汽轮机叶片减振。NOPD将适当数量的阻尼性颗粒材料填充到振动结构体的孔洞或附加中空容器中，当结构体产生振动时，利用颗粒与容器壁、颗粒与颗粒之间发生的碰撞和摩擦，消耗结构振动能量，从而达到衰减结构振动的目的[3-6]。现今，一些学者在颗粒阻尼技术的基础上提出了颗粒阻尼吸振器(tuned particle damper，TPD)的概念并对其进行了深入研究。姚冰等[7]对颗粒阻尼吸振器进行了实验研究。实验结果表明，颗粒阻尼吸振器在主系统加速度幅值小于1g(g为重力加速度)的情况下，仍具有较强的减振能力，克服了颗粒阻尼器在微振动时失效的问题。杨智春等[8]提出了一种颗粒阻尼吸振器设计概念，所设计的颗粒阻尼吸振器(颗粒碰撞阻尼吸振器)拓宽了单质量块动力吸振器的工作频带。许维炳等[9]把颗粒阻尼技术引入到桥梁减振领域，提出了一种颗粒阻尼吸振器(调频型颗粒阻尼器)方案，该吸振器与单质量块动力吸振器(调谐型阻尼器)相比，具有更宽的减振频带。

迄今为止，学者们所研究的颗粒阻尼吸振器均采用固定的系统参数，即一经设计定型，其颗粒质量及刚度都不能改变。研究表明[8-9]，这种颗粒阻尼吸振器相对于传统的单质量块动力吸振器能够拓宽有效减振频带，但频带增加的幅度有限。当外界激励频率超出吸振器有效减振频带时，减振效果会变差。为了进一步拓宽颗粒阻尼吸振器的有效减振频带，本文在颗粒阻尼吸振器[7-9]和变质量动力吸振器[10]的基础上，提出了一种变质量颗粒阻尼吸振器，通过对吸振器质量的调节，获得宽频减振性能。

由于颗粒阻尼碰撞和摩擦减振的机理非常复杂，以及影响其性能的因素(颗粒的形状、密度、填充率、激励的频率和幅值等)较多[11-14]，建立一个精确的数学模型相对困难，因此本文借鉴文献[7]提出的近似模型，并考虑容器中液体的影响，利用近似模型及实验对变质量颗粒阻尼吸振器的宽频减振性能进行研究。

1变质量颗粒阻尼吸振器的理论模型

变质量颗粒阻尼吸振器模型如图1所示，图中，m1、k1、x1分别为主系统的质量、刚度和位移；m2、ma、mf、k2、x2分别为颗粒容器质量、颗粒质量、可变液体质量、吸振器的刚度和位移；x0为外界激励。可变液体质量mf能够在最小值mfmin与最大值mfmax之间变化，因此可以通过调节可变液体质量mf的大小调节吸振器最佳减振频率，追踪外界激励频率的变化，在较宽的频带内获得最佳减振效果。

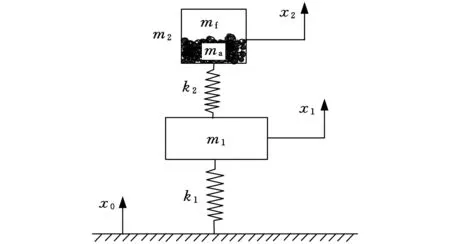
图1　变质量颗粒阻尼吸振器模型

由于颗粒阻尼具有强非线性特性，对其进行理论分析比较困难，因此有必要建立一个等效的颗粒阻尼模型。颗粒阻尼吸振器阻尼由发生碰撞和摩擦作用颗粒的集合效应组成，采用文献[7]的处理方法，利用一个阻尼器和质量块来等效众多颗粒在同一加速度下的动力学行为，则图1所示模型被近似成三自由度系统，如图2所示。

图2　变质量颗粒阻尼吸振器等效模型

图2中，mp为发生跳动并产生阻尼作用颗粒(在一定加速度下，可能只有部分颗粒产生跳动和阻尼作用)的质量，称为等效视在质量；x3为等效视在质量的位移；等效阻尼c为产生阻尼作用颗粒的等效黏性阻尼；mc为颗粒容器和未产生阻尼作用颗粒(附在容器上未跳动颗粒)的总质量。mp、c和mc的取值皆与吸振器加速度、可变液体与颗粒混合的比例有关，且mp与mc之和始终等于颗粒容器与颗粒的总质量，即

mp+mc=m2+ma

(1)

由于颗粒阻尼的强非线性特性，很难找出等效阻尼比与系统参数的关系式，因此，借鉴单自由度系统的阻尼比定义，得到等效阻尼比：

(2)

产生阻尼作用颗粒的质量mp在一定程度上代表着吸振器的耗能情况。当产生阻尼作用颗粒的质量mp较大时，产生的等效黏性阻尼比ξ较大；当产生阻尼作用颗粒的质量mp较小时，产生的等效黏性阻尼比ξ较小。根据这种物理推断，可得颗粒阻尼吸振器的质量分配方案中的mp和mc[7]：

(3)

变质量颗粒阻尼吸振器动力学模型是非线性的，尤其当可变液体与颗粒混合的比例发生变化时，等效视在质量mp、等效阻尼c、颗粒容器和未产生阻尼作用颗粒的总质量mc皆会非线性改变，此模型非常复杂，为了简化模型，本文忽略可变液体与颗粒混合比例变化对等效阻尼c的影响。因此，图2所示系统的运动微分方程可表示为

(4)

为了研究变质量颗粒阻尼吸振器的宽频减振性能，利用MATLAB对式(4)所示模型进行仿真。笔者自行给定一组结构参数值，见表1。

表1　仿真模型量纲一参数

颗粒容器内可变液体质量mf在最小值mfmin=0.02与最大值mfmax=0.10之间变化时，利用MATLAB仿真所得主系统幅频响应函数曲线如图3所示。

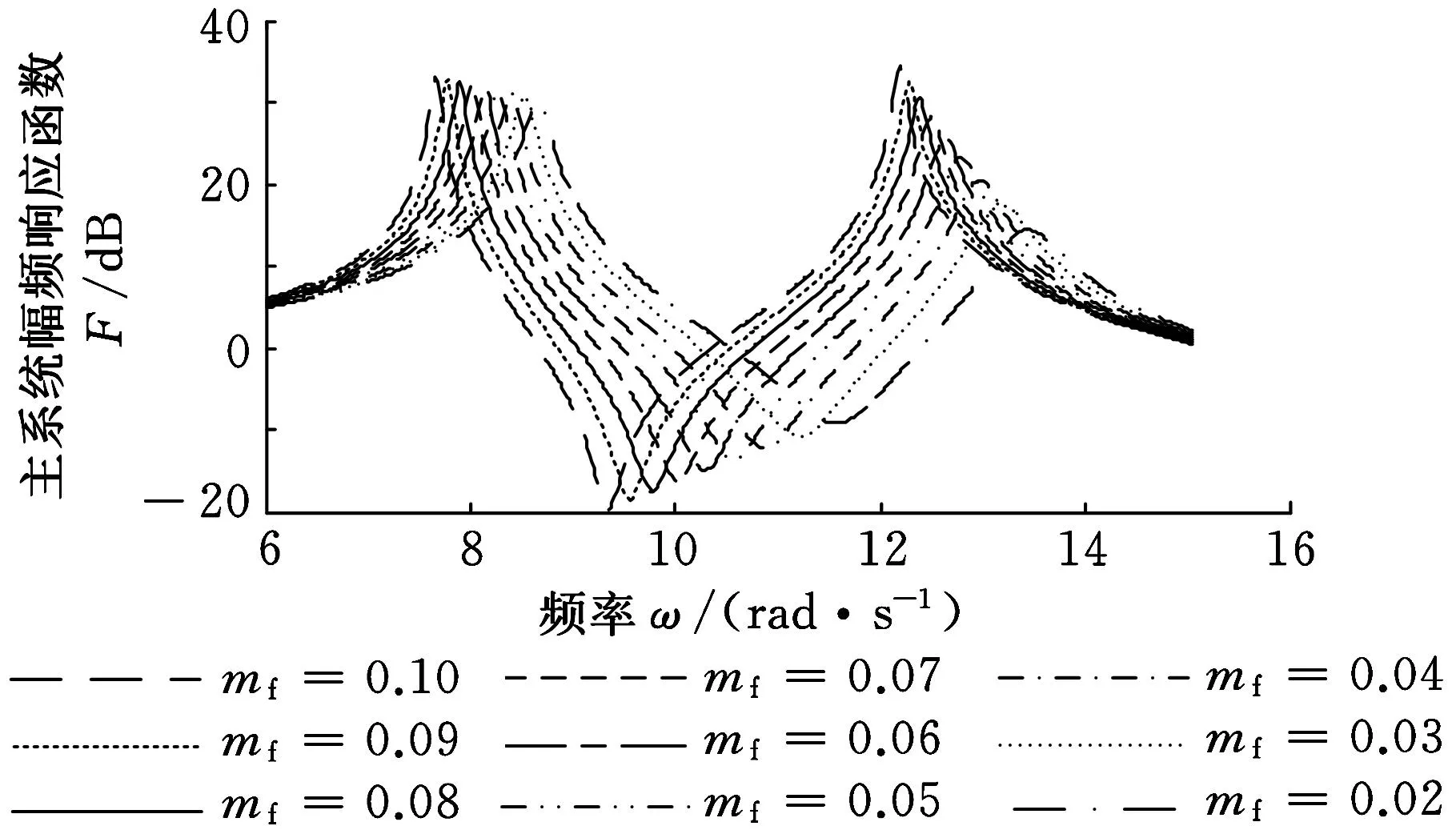
图3　仿真所得主系统幅频响应函数

从图3可以看出：对于单一液体质量来说，吸振器的有效减振频带都较窄；主系统幅频响应函数的最低点随着液体质量mf的增加而逐渐向左移动。当液体质量mf取最小值0.02时，吸振器最佳减振频率为11.58rad/s，当液体质量mf为最大值0.10时，最佳减振频率为9.34rad/s。由于液体质量mf可在最小值mfmin与最大值mfmax之间连续变化，因此通过调节吸振器液体质量，能够使吸振器在9.34～11.58rad/s之间的频带内获得有效减振，从而显著地拓宽有效减振频带。

需要说明的是，本文采用的变质量颗粒阻尼吸振器理论模型是根据颗粒阻尼的特点而作出的一种假设，更精确模型的研究将会在后续工作中展开。

2变质量颗粒阻尼吸振器宽频减振性能实验研究

为了验证变质量颗粒阻尼吸振器的宽频减振性能，搭建了悬臂梁实验系统，如图4所示。

图4　实验系统

图4中，A、B分别表示主系统和变质量颗粒阻尼吸振器系统。主系统由钢板弹簧、质量块及加速度传感器组成，其分别为弹性元件和质量元件。吸振器由一个较小型号的钢板弹簧、颗粒容器、容器内颗粒和液体四部分组成，它们分别为弹性元件、固定质量、颗粒阻尼元件和可变液体质量。其中，充当阻尼元件的颗粒为直径2mm的不锈钢金属圆珠，其总质量为5g；选用水作为吸振器变质量介质，水量可在1.8～9.3mL之间连续变化。

实验系统所需仪器包括信号发生器、功率放大器、激振器、振动加速度传感器、电荷放大器、数据采集仪和笔记本电脑。信号发生器产生的振动信号，经功率放大器放大后输出给激振器，激振器驱动主系统振动。传感器从主系统和激振器处采集振动信号，该振动信号经电荷放大器放大、滤波后被数据采集仪采集并传输到电脑上。电脑通过数值采集软件将采集到的振动数据接收、存储，分析颗粒阻尼吸振器对主系统的减振效果。实验主要探讨颗粒容器内水量变化对吸振器宽频减振性能的影响，因而，在实验过程中，保持激励信号电压固定，统一采用2V。

利用上述设计的实验系统，测试5～40Hz范围内不同水量条件下的主系统幅频响应函数，实验结果如图5所示。从图5可以看出，主系统固有频率约为23.5Hz；安装变质量颗粒阻尼吸振器后，当容器内水量为9.3mL、4.3mL和1.8mL时，吸振器分别在19.7Hz、23.0Hz、26.6Hz处对主系统实现了12.71dB、13.42dB、14.08dB的振动衰减。吸振器液体质量的变化引起了最佳减振频率的改变，这与图3的理论模型计算结果相一致。但是，图3的第一个共振峰随着液体质量的增加而稍微升高，最低点随着液体质量的增加而降低，这与实验所测结果不相符。我们认为造成这一偏差的主要原因是所建立的颗粒阻尼模型还不够精确。利用实验中容器内水量为9.3mL、4.3mL和1.8mL，以及水量为 6.7mL、2.9mL两次附加实验的数据，对颗粒容器内水量与吸振器最佳减振频率之间的关系进行分析，并使用最小二乘法对实验数据进行拟合处理，所得曲线如图6所示。该曲线可用以下公式表示

(5)

式中，V为颗粒容器内水量，mL；fa为吸振器最佳减振频率，Hz。

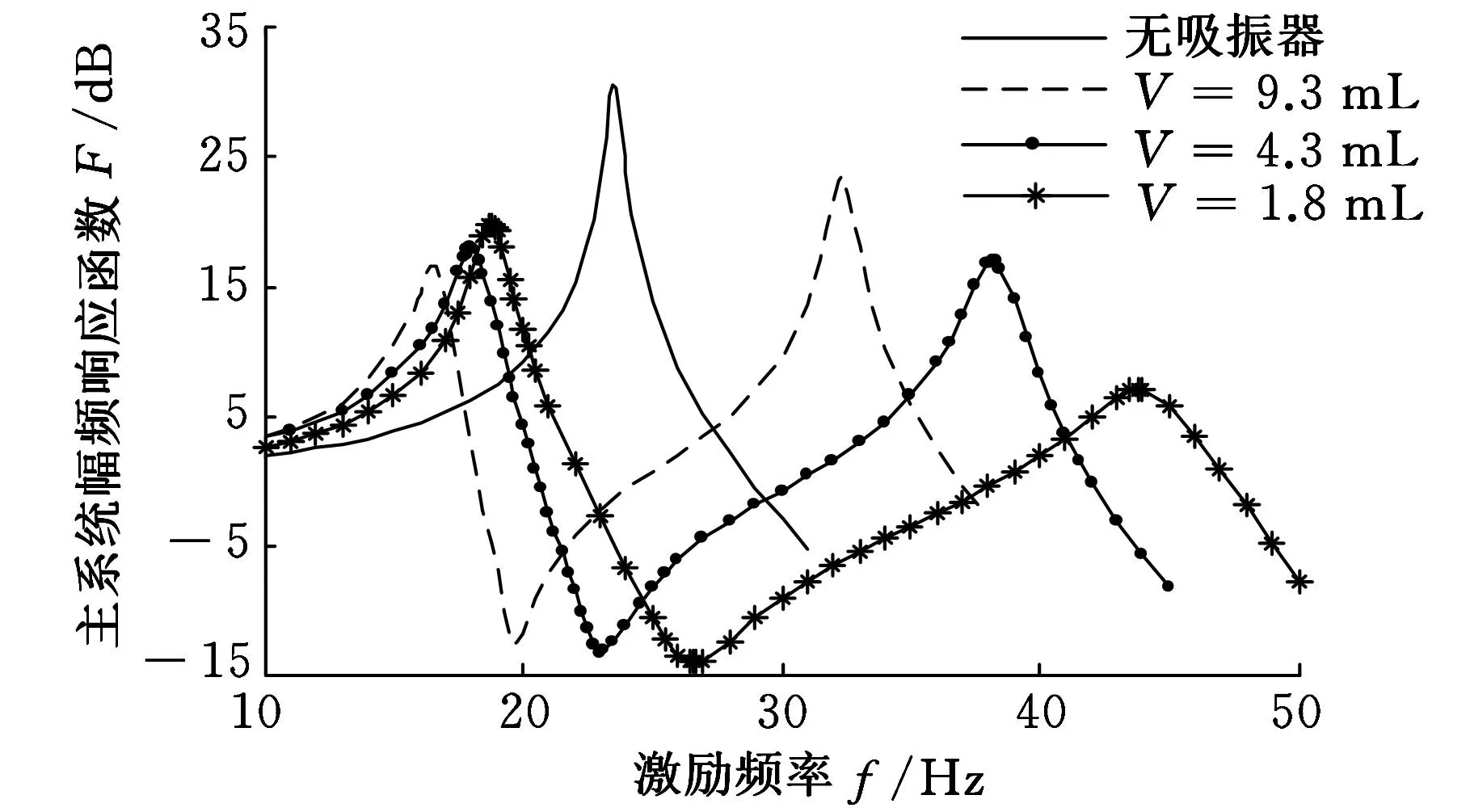
图5　实验所得主系统幅频响应函数

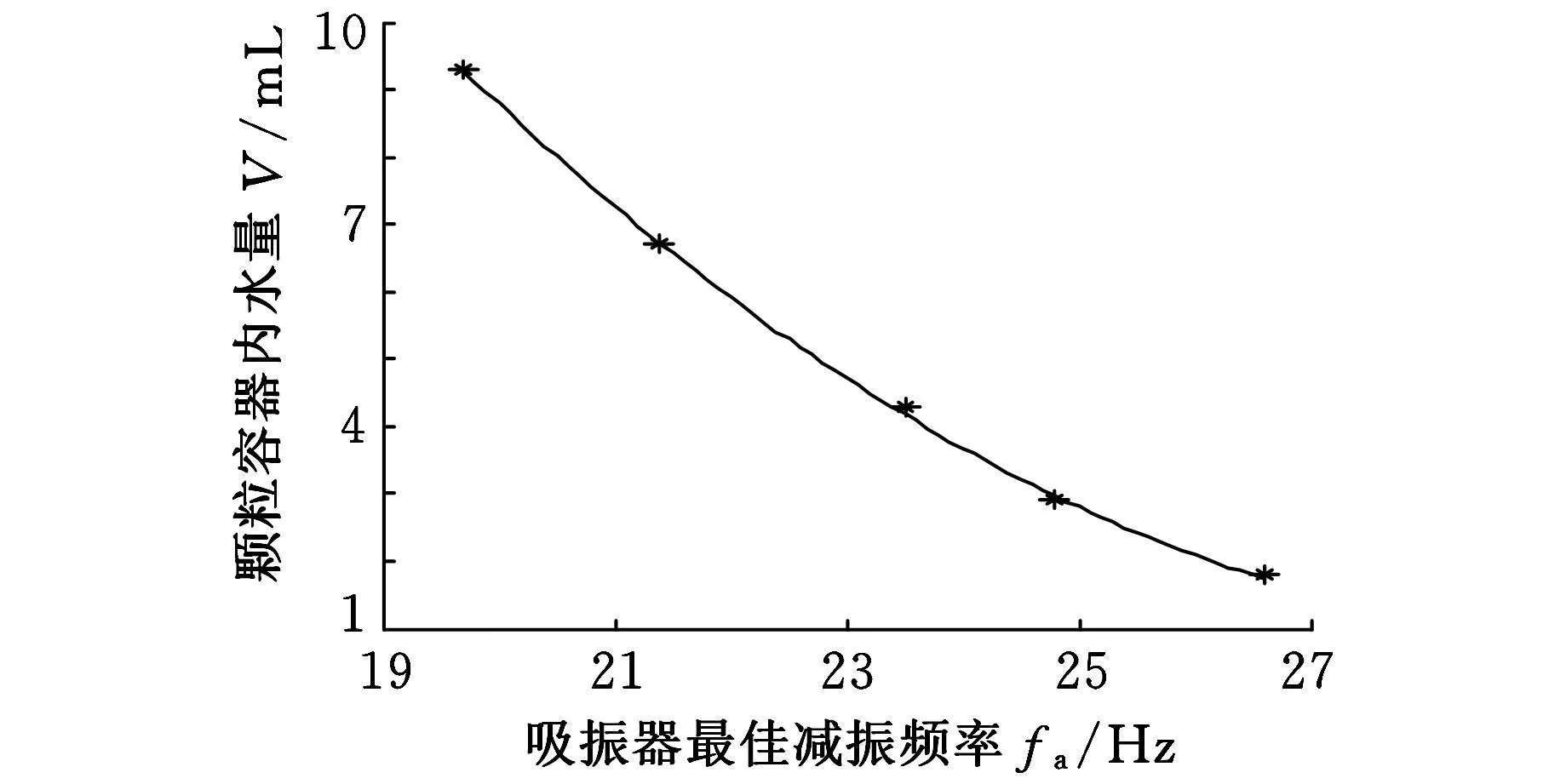
图6　容器内水量与最佳减振频率之间的关系

从图5还可以看出：尽管在水量一定(例如容器内水量为4.3mL)时，吸振器有效减振频带并不宽，但当容器内水量在1.8～9.3mL之间连续变化时，就可以获得较大的有效带宽，如图7所示，图中，点A、B、C分别为容器内水量为9.3mL、4.3mL、1.8mL时，主系统幅频响应函数的最低点。当激励频率位于点A左边时，容器内水量取9.3mL，位于点C右边时取1.8mL，点A与C之间的水量按式(5)计算。通过调节颗粒容器内水量，吸振器获得了19.7～26.6Hz之间约6.9Hz的有效减振频带，宽频减振性能得到显著提高。

图7　主系统幅频响应函数

为了验证变质量颗粒阻尼吸振器的减振性能，利用图4所示实验系统对其进行了时域研究。初始时刻颗粒容器内水量为1.8mL，激振器激励频率为26.6Hz，此时吸振器处于调谐状态，在实验进行到10s、25.5s和41.6s时分别把激励频率调整为24.8Hz、23.5Hz和19.7Hz，接下来在16.2s、32.3s和48.6s时，根据式(5)调节容器内水量使主系统重新处于调谐状态，实验所得结果如图8所示。

图8　实验所得主系统时域响应

从图8可以看出：在第10s、25.5s和41.6s时，激励频率变化引起减振效果显著变差，主系统加速度幅值分别上升至6.3m/s2、6.0m/s2、6.2m/s2；在第16.2s、32.3s和48.6s时，调节颗粒容器内的水量使吸振器重新处于调谐状态，主系统加速度幅值分别下降到1.9m/s2、2.0m/s2、1.8m/s2，下降约69.84%、66.67%、70.97%，减振效果显著。

从以上频域和时域实验结果均可得出：本文所提出的变质量颗粒阻尼吸振器具有良好的宽频减振性能。

3结论

(1)本文提出了一种变质量颗粒阻尼吸振器方案，将颗粒容器作为变质量单元，通过改变颗粒容器内液体质量，调节吸振器最佳减振频率。

(2)实验数据表明：与定质量颗粒阻尼吸振器相比，变质量颗粒阻尼吸振器可以在更宽频带内衰减主系统振动，具有良好的宽频减振性能。

(3)外界激励幅值对变质量颗粒阻尼吸振器的减振性能也具有一定影响，因此，如何确定颗粒容器内液体量与外界激励频率和幅值的关系，如何对变质量颗粒阻尼吸振器进行快速、精确的控制将是进一步研究的重点。

参考文献：

[1]Panossion H V，Johnson V J，Rogers L. Non-obstructive Impact Damping Application for Cryogenic Environments[C]//Proceeding of Damping 89. San Diego，California，USA，1989：1-9.

[2]Panossion H V，Johnson V J，Rogers L.NOPD Tests on Aluminum Beams[C]//Proceeding of Damping 91. San Diego, California，USA，1991：13-15.

[3]徐志伟，陶宝祺，黄协清. OPD颗粒减振机理的理论及实验研究[J]. 航空学报，2001，22(4)：347-350.

Xu Zhiwei，Tao Baoqi，Huang Xieqing. Theoretical and Experimental Research on Vibration Absorption Mechanisms of NOPD Particle[J]. Acta Aeronautica et Astronautica Sinica, 2001,22(4)：347-350.

[4]胡溧，黄其柏，许智生. 颗粒阻尼的回归分析研究[J]. 中国机械工程，2008，19(23)：2834-2837.

Hu Li，Huang Qibai，Xu Zhisheng. Regression Analysis of Particle Damping[J]. China Mechanical Engineering，2008，19(23)：2834-2837.

[5]鲁正，吕西林，闫维明. 颗粒阻尼技术研究综述[J]. 振动与冲击，2013,32(7)：1-7.

Lu Zheng，Lü Xilin，Yan Weiming. A Survey of Particle Damping Technology[J]. Journal of Vibration and Shock，2013，32(7)：1-7.

[6]胡溧，黄其柏，柳占新，等. 颗粒阻尼的动态特性研究[J]. 振动与冲击，2009，28(1):134-137.

Hu Li，Huang Qibai，Liu Zhanxin，et al. Dynamic Characterstics of Particle Dampers[J]. Journal of Vibration and Shock，2009，28(1)：134-137.

[7]姚冰，陈前，项红萤，等.颗粒阻尼吸振器试验研究[J].振动工程学报，2014，14(2):201-207.

YaoBing，ChenQian，XiangHongying，etal.TheExperimentalStudyonDynamicPropertiesofTunedParticleDamper[J].JournalofVibrationEngineering，2014，14(2)：201-207.

[8]杨智春，李泽江.颗粒碰撞阻尼动力吸振器的设计及试验研究[J]. 振动与冲击，2010，29(6)：69-71，143.

YangZhichun，LiZejiang.DesignandTestforaTypeofParticleImpactDampedDynamicAbsorber[J].JournalofVibrationandShock，2010，29(6)：69-71，143.

[9]许维炳，闫维明，王瑾，等. 调频型颗粒阻尼器与高架连续梁桥减震控制研究[J]. 振动与冲击，2013，32(23)：95-99.

XuWeibing，YanWeiming，WangJin，etal.ATunedParticleDamperandItsApplicationinSeismicControlofContinuousViaducts[J].JournalofVibrationandShock，2013，32(23)：95-99.

[10]高强，房祥波，赵艳青，等. 变质量动力吸振器及其减振性能[J]. 长安大学学报(自然科学版)，2013，33(5)：109-112.

GaoQiang，FangXiangbo，ZhaoYanqing，etal.VariableMassDynamicAbsorberandItsPerformanceofVibrationReduction[J].JournalofChang’anUniversity:NaturalScienceEdition, 2013，33(5)：109-112.

[11]FowlerBL，FlintEM，OlsmSE.EffectivenessandPredictabilityofParticleDamping[C]//ProceedingsofSPIEConf.onDampingandIsolation.NewportBeach，CA，USA，1999：1155-1166.

[12]MaoKM，WangYM，XuZW，etal.SimulationandCharacterizationofParticleDampingIntransientVibrations[J].JournalofVibrationandAcoustics-TransactionsoftheASME, 2004，126(2)：202-211.

[13]LuZ,LuXL,MasriSF.StudiesofthePerformanceofParticleDampersunderDynamicLoads[J].JournalofSoundandVibration，2010，329：5415-5433.

[14]MarhadiKS，KinraVK.ParticleImpactDamping:EffectofMassRatio，Material，andShape[J].JournalofSoundandVibration，2005，283：433-448.

(编辑张洋)