广义棱柱中的超欧拉有向图
牛兆宏,冯雅琼,王刘岩
(山西大学 数学科学学院,山西 太原 030006)
0 引言
本文只考虑有限无环的图和有向图,没有特殊说明的话,图指的是无向图。文中未定义的符号和术语,无向图参见文献[1],有向图参见文献[2]。

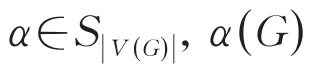
定理1[9]设G是n个顶点的连通图。如果G∈F,那么对于任意的 α∈Sn,α(G)都是超欧拉图。
一个有向图称为是欧拉有向图,是指它有一条包含所有弧的闭迹。如果一个有向图D包含一个生成欧拉子有向图,则称D是超欧拉有向图。文献[15]和[16]给出了若干有向图是超欧拉图的充分条件。
受到广义棱柱较多的研究成果及应用、以及有向图的超欧拉性的相关研究的启发,本文主要讨论两个有向图的广义棱柱的超欧拉性质。我们将无向图G的广义棱柱的概念推广到有向图上,给出了如下定义(最后一节将指出这一定义与图G的α-广义棱柱α(G)的联系)。设D和H是两个有向图,记
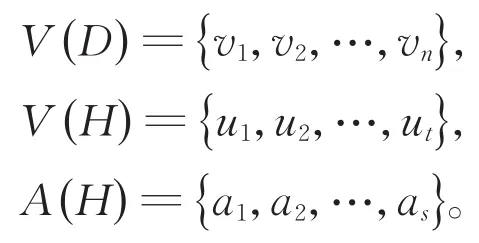

下文中,第1节介绍与置换α有关的记号,并且给出一个判断广义棱柱的超欧拉性质的引理。第2节证明了两个超欧拉有向图的广义棱柱一定是超欧拉有向图,并且利用上一节的引理给出了一类由有向可迹图和超欧拉有向图所构造的广义棱柱是超欧拉有向图的一个特征刻画。作为主要结果的推论,最后一节讨论了无向图的广义棱柱的超欧拉性质。
1 预备知识
对每个有向图D,对应的有一个无向图G,它的顶点集与D相同,且对D的每条弧,G中有一条对应边与它有相同的端点。称G为有向图D的基础图。如果一个有向图D的基础图是连通的,则称D是连通的。如果对于任意一对顶点x,y∈V(D),D中都存在从x到y的有向路和y到x的有向路,则称D是强连通的。下面的定理是有向图版本的欧拉定理。
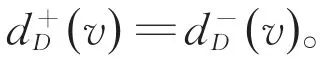
设α∈Sn是一个置换,并且设α是r个轮换的乘积B1B2…Br。在不引起混淆的前提下,Bi表示α中的某个轮换,也表示该轮换中所含元素构成的集合。为了证明过程中表述方便,引入如下的符号和术语。在α的每一个轮换Bi中,记ci=min(Bi)和fi=max(Bi),并且在表示轮换Bi时,总是约定最小元位于该轮换的第1个位置,同时将该轮换简记作 Bi=(ci…fi…)。若 ci=fi,则 Bi=(ci)。在将置换α表示成轮换之积时,按照每个轮换中最小元从小到大的次序排列这些轮换。这时,我们将置换α表示为

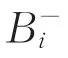
下面给出一个判断广义棱柱是超欧拉有向图的引理。
引理3 设P是一条n个顶点的有向路,H是超欧拉有向图,α=B1B2…Br∈Sn是一个置换。如果存在一个轮换Bl∈α,使得对于α中其他任意一个轮换Bi,cl 因为H是超欧拉有向图,所以它有一个生成欧拉子有向图S′。注意到任意一个欧拉有向图都可以分解为一些弧不交的有向圈。我们将S′分解出的弧不交的有向圈记为C1,C2,…,Cm。不妨设C1=u1u2…un1u1。 在A(S)中,我们记弧子集 综上所述,引理得证。 本节讨论两个有向图的广义棱柱的超欧拉性质。 定理4 设D和H是超欧拉有向图,|V(D)|=n,那么对于任意的α∈Sn,D对H的α-广义棱柱αH(D)是超欧拉有向图。 下面利用引理3,给出了P是有向路,H是超欧拉有向图,并且在α中所含轮换个数r≤3时,αH(P)是超欧拉有向图的一个特征刻画。 定理5 设P是一条n个顶点的有向路,H是超欧拉有向图,α=B1B2…Br∈Sn是一个置换。如果r≤3,那么P对H的α-广义棱柱αH(P)是超欧拉有向图当且仅当α连通。 证明 首先证明充分性。我们断言在定理5的条件下,对于Sn中的任意一个置换α=B1B2…Br,一定存在一个轮换Bl∈α,使得对于α中其他任意一个轮换Bi,cl 若r=1,置换α中只含一个轮换B1,显然断言成立。若r=2,即α=B1B2,取Bl=B1,由于α是连通的,所以c1 由该断言和引理3可知,αH(P)是超欧拉有向图。充分性得证。 这就证明了定理5。 如果有向图D包含一条生成有向路,那么称它是有向可迹图。由定理5,可以得出下面的推论。 推论6 设D是n个顶点的有向可迹图,H是超欧拉有向图,α=B1B2…Br∈Sn是一个置换。如果α连通,并且r≤3,那么D对H的α-广义棱柱αH(D)是超欧拉有向图。 证明 D是有向可迹图,取它的一条生成有向路P。由于α∈Sn且α连通,所以由定理5可知,αH(P)是超欧拉有向图。因为αH(P)是αH(D)的生成子有向图,所以αH(D)也是超欧拉有向图。证毕。 针对两个无向图G和H,可将有向广义棱柱αH(D)的定义稍做修改,把H的每个顶点替换为G的一个复制,而把H的每一条边替换为一组置换边,即得无向广义棱柱αH(G),那么α(G)≅αK2(G),其中K2为两个顶点的完全图。这说明了由两个图G和H构造的广义棱柱αH(G),是文献[3]中定义的一个图G的α-广义棱柱α(G)的推广。 由定理4和推论6,很容易得到如下无向图的广义棱柱的超欧拉性质。 推论7 设G和H是超欧拉图,|V(D)|=n,那么对于任意的α∈Sn,G对H的α-广义棱柱αH(G)是超欧拉图。 推论8 设G是n个顶点的可迹图,H是超欧拉图,α=B1B2…Br∈Sn是一个置换。如果α连通,并且r≤3,那么G对H的α-广义棱柱αH(G)是超欧拉图。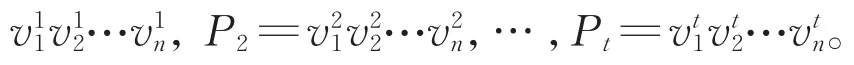
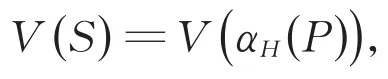

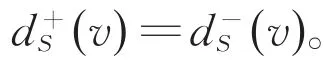

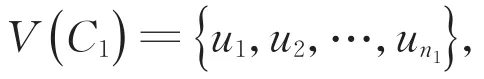

2 有向广义棱柱的超欧拉性质

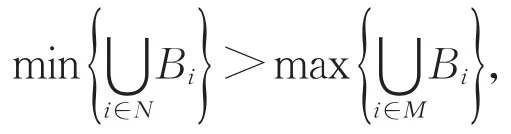
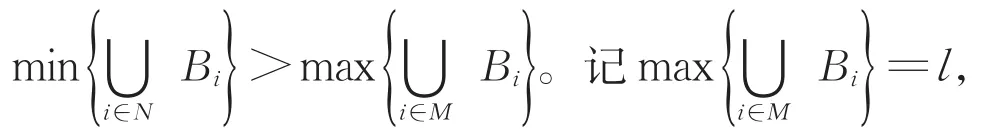
3 无向广义棱柱的超欧拉性质

