局部外竞赛图上的二次外邻
李瑞娟,孙志浩
(山西大学 数学科学学院,山西 太原 030006)
0 引言
设D=(V,A)是一个有向图,其中V(D)和A(D)分别表示D的顶点集和弧集。对于任意的顶点x,y∈V(D),如果(x,y)∈A(D),则称(x,y)是D的一条弧,y称为x的外邻点,x称为y的内邻点。设H是D的任意一个顶点子集,也可用H表示其在D上的导出子图,对D的任意的一个顶点x,它在H上的内邻点集和外邻点集分别记为:
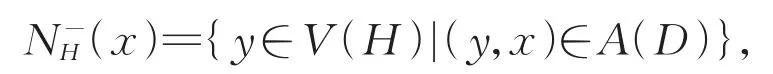
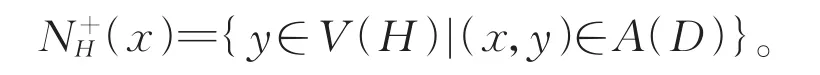
同样,对任何顶点子集S⊂V(D),它在H上的内邻点集和外邻点集记为:
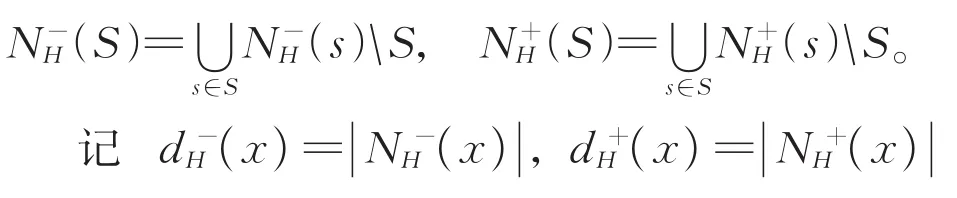
分别为x在H上的入度和出度。x在H上的二次外邻点集和二次内邻点集记为:
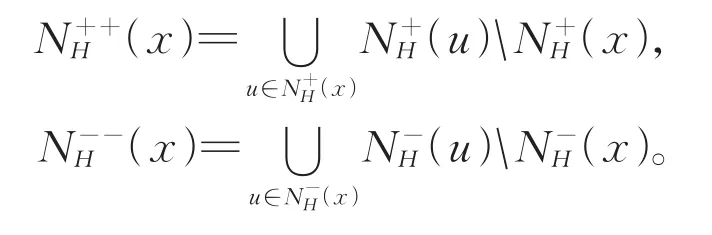
记d++H(x)=|N++H(x)|,d−−H(x)=|N−−H(x)|。以上若H=D,则可省略H。有向图D的最小入度和最小出度分别为:
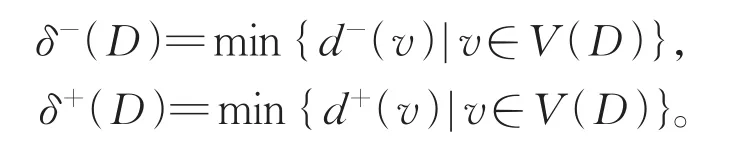
设X,Y是D的两个不相交的顶点子集,从X到Y的弧集表示为:E(X,Y)={(x,y)∈A(D)|x∈X,y∈Y},记e(X,Y)=|E(X,Y)|表示X到Y的弧的数目。
在本文的讨论中,考虑的所有的圈都是有向圈。有向图D的围长g(D)是D的最小圈的长度。若 g(D)≥k+1,即D没有圈长小于等于k的圈,其中k≥2,则称有向图D是k-free的。本文中所考虑的有向图都是无环且无2-圈的,一些未定义的基本符号参见文献[1]。
1990年,Seymour提出了猜想1。
猜想 1[2](Seymour二次邻域猜想)任何无环无2-圈的有向图总存在一个顶点v,使得d++(v)≥d+(v)。
为方便起见,将满足猜想1的顶点称为图的Seymour顶点。
称有向图D是半完全有向图,如果对于任意的顶点x,y∈V(D),或有 (x,y)∈A(D),或有(y,x)∈A(D),或有 (x,y)∈A(D)且 (y,x)∈A(D)。若半完全有向图D无2-圈,则称其为竞赛图。Fisher[3]用概率方法证明了对于任何竞赛图都存在一个Seymour顶点,即定理1。Havet和Thomassé[4]用中间序的方法也给出了这个定理的证明,并证明了不包含出度为0的点的竞赛图中至少有两个Seymour顶点。
定理1[3]每个竞赛图中都有一个Seymour顶点。
2001 年,Kaneko 和 Locke[5]证明了任何最小出度小于7的有向图都有一个Seymour顶点,2007 年,Fidler和 Yuster[6]进一步使用了中间序方法,证明了Seymour二次邻域猜想分别在最小度为|V(D)|−2的定向图、竞赛图减去一个星以及竞赛图减去一个子竞赛图的弧集等图的正确性。在 2008 年,Hamidoune[7]证明了任何点传递有向图都存在一个Seymour顶点。2012 年,Ghazal[8]中利用加权的中间序方法证明了猜想1对于竞赛图去掉一个广义星得到的有向图成立。在2013年,Lladó[9]证明了任何r出度正则且连通度至少为r−1的有向图都存在一个Seymour顶点。在2021年,Bouya和Opo⁃rowski用线性代数的语言重新陈述了Seymour二次邻域猜想,给出了若干等价命题,以期通过代数的观点解决这个问题[10]。
研究Seymour二次邻域猜想的另一种方法是在一个有向图D中,确定最大实数 λ,使得存在一个顶点v满足d++(v)≥λd+(v)。Sey⁃mour二次邻域猜想要求 λ=1。2003年,Chen等[11]证明了 λ=0.657 298...是方程 2x3+x2−1=0 的唯一实根。2010年,Zhang和Zhou[12]证明了对于任何3-free有向图D存在一个顶点v满足d++(v)≥ λd+(v),这里λ=0.675 130...是方程x3+3x2−x−1=0在区间(0,1)上的唯一实根。在 2017年,Liang 和 Xu[13]考虑了kfree有向图(k≥3),证明了d++(v) ≥ λkd+(v),这里 λk是多项式
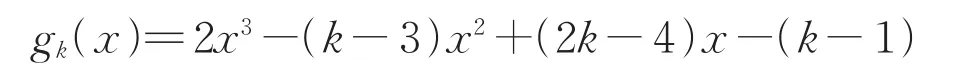
在区间(0,1)上的唯一实根。并且 λk随着k的单调递增而趋于1的,即当k→∞时有 λk→1。当k=3时,λk=0.682 327...。 2019年 ,Chen和Chang改进了在3-free有向图上的结果,给出了定理2。
定理2[14]设D是一个3-free有向图,则存在一个顶点v∈V(D),使得d++(v) ≥λd+(v),这里λ=0.695 860… 是方程在区间(0,1)上的唯一实根。
本文将在局部外竞赛图上研究这个猜想,从局部外竞赛图的定义和结构出发,确定最大实数 λ,使得存在一个顶点v满足d++(v)≥λd+(v)。并在某些限制条件下,如终止强分支无3-圈,得到了更好的下界。
1 准备工作
定义1[1]若对任意的x∈V(D),N+(x)(N−(x))的诱导子图是半完全有向图,则称有向图D是局部外(内)半完全有向图。并且若有向图D既是局部外半完全有向图又是局部内半完全有向图,则称D为局部半完全有向图。

图1 (a)一个局部外半完全有向图;(b)一个局部半完全有向图Fig.1 (a)A locally out-semicomplete digraph;(b)A locally semicomplete digraph
定义2[1]无2-圈的局部外(内)半完全有向图称为局部外(内)竞赛图。同样,无2-圈的局部半完全有向图称为局部竞赛图。
显然,每个竞赛图都是局部外(内)竞赛图,也是局部竞赛图。为进一步叙述主要结论,介绍下面一些概念。
称有向图是连通的,如果它的基础简单图是连通的。称有向图D是强连通的(简称强的),如果对任意顶点x,y∈V(D),都存在从x到y的有向路。若D不是强连通的,则D存在强连通分解:D1,D2,…,Dp,其中Di(1≤i≤p)为D的强连通分支(简称强分支)且
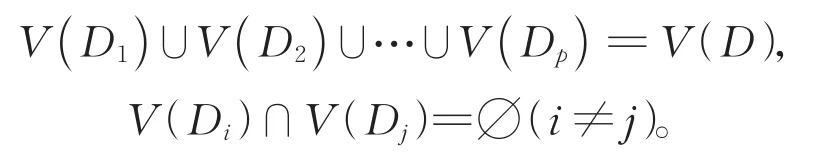
D的强分支可依次被标记为D1,D2,…,Dp,并且不存在Dj到Di(i 引理1[1]每个连通的局部外(内)半完全有向图D有一个入(出)分枝。 定理3[1]已知D是一个局部外半完全有向图,则 (1)设A和B是D的两个不同的强分支,若有顶点b∈B被A中的某一个顶点所控制,则b被A中所有顶点所控制,即A↦b。 (2)若D是连通的,则D的强分支有向图SC(D)有一个入分枝。 定理4[1]连通有向图D包含一个入(出)分枝当且仅当D仅有一个终止(初始)强分支。 图2是一个非强连通的局部外半完全有向图,大圆圈表示强分支,在两个强分支之间从分支A到分支B的粗弧表示至少存在一个顶点b∈B,使得A↦b。 图2 一个非强连通的局部外半完全有向图的强连通分解Fig.2 Strong decomposition of a non-strong locally out-semicomplete digraph 本文的一些相关证明依赖局部外(内)竞赛图的结构特征,上述关于局部外(内)半完全有向图的定义和定理显然对于局部外(内)竞赛图也适用。 定理5对于任意的局部外竞赛图D,总存在一个顶点v∈V(D),使得d++(v)≥ λd+(v),这 里 λ=0.689 897…是 方程 5x2−2x−1=0的唯一正实根。 证明对于只有1个或2个顶点的有向图,定理5显然是成立的。设D是一个有n≥3个顶点的局部外竞赛图,用反证法,假设D中不存在满足d++(v)≥λd+(v)的顶点,即对任意的 顶 点v∈V(D),有d++(v)< λd+(v),这 里λ=0.689 897…是方程 5x2−2x−1=0的唯一正实根。 由于每个局部竞赛图都是局部外竞赛图,则有下面的推论成立。 推论1对于任意的局部竞赛图D,总存在一个顶点v∈V(D),使得d++(v)≥λd+(v),这里 λ=0.689 897…是方程 5x2−2x−1=0的唯一正实根。 Caccetta-Häggkvist猜想叙述为最小出度不小于r的n阶有向图含有长度不大于的有向图。下面的命题描述了Caccetta-Häggkvist猜想与Seymour二次邻域猜想的关系。 命题1[11]对于一个含有n个顶点的无环且无2-圈的有向图D,若存在一个顶点v∈V(D),使得d++(v)≥λd+(v),这里λ是一个正实数。如果 min{δ−(D),δ+(D)}≥n/(2+λ),则有向图D有3-圈。 由命题1可以看出,当最小入度和最小出度都至少是n/3时,即λ=1时,Seymour二次邻域猜想蕴含了Caccetta-Häggkvist猜想中含有长度为3的有向圈的情况。对于局部外竞赛图,可得出以下推论。 推论2设D是一个含有n个顶点的局部外竞赛图,如果 min{δ−(D),δ+(D)}≥0.3717n,则D包含3-圈。 证明由定理5知,存在一个顶点v∈V(D),使d++(v)≥λd+(v),这里λ=0.689 897…是方程 5x2−2x−1=0的唯一正实根。又由命题1知,若min{δ−(D),δ+(D)}≥0.3717n,也就有min{δ−(D),δ+(D)} ≥n/(2+λ),所以D包 含3-圈。 下面考虑局部外竞赛图的终止强分支上的二次外邻。由引理1知,局部外竞赛图有一个入分枝。又根据定理4可得,局部外竞赛图仅有一个终止强分支。 引理2对任意非强连通的有向图D,它的终止强分支上的Seymour顶点也是整个有向图上的Seymour顶点。 证明对任意非强连通的有向图D都存在强分支无圈序,所以至少存在一个终止强分支,记D的一个终止强分支为Dt。若Dt中存在一个Seymour顶点v,使得由于不存在从Dt中发出的到其他强分支的弧,有且,从而,所以v也是D的Seymour顶点。 引理3局部外竞赛图的初始强分支和终止强分支也是局部外竞赛图,且局部外竞赛图的终止强分支上的Seymour顶点也是整个局部外竞赛图上的Seymour顶点。 证明设D是一个局部外竞赛图,显然D的任意顶点子集诱导的子有向图是局部外竞赛图,因此,D的初始强分支和终止强分支仍然是局部外竞赛图。再由引理2可知,局部外竞赛图的终止强分支上的Seymour顶点也是整个局部外竞赛图上的Seymour顶点。 推论3若局部外竞赛图D的终止强分支只包含一个顶点v,则顶点v是D的一个Seymour顶点。 定理6如果局部外竞赛图D的终止强分支Dt不包含3-圈,则存在一个顶点v∈V(D),使得d++(v)≥ λd+(v),这里λ=0.695 860…是方程在区间(0,1)上的唯一实根。 证明设局部外竞赛图D的终止强分支为Dt。若Dt不包含3-圈,即Dt是3-free有向图,由定理2知,存在一个顶点v∈V(Dt),使得,又根据引理2的证明可知,有,从而存在一个顶点v∈V(Dt)⊂V(D),使得d++(v) ≥ λd+(v),这里 λ=0.695 860…是方程在区间(0,1)上的唯一实根。 注记由于局部内竞赛图可以看成是某个局部外竞赛图的逆图,以及定理6的证明,易知下面的结论成立: (1)对于任意的局部内竞赛图D,总存在一个顶点v∈V(D),使得d−−(v)≥λd−(v),这里λ=0.689 897…是方程 5x2−2x−1=0的唯一正实根。 (2)如果局部内竞赛图D的一个终止强分支Dt不包含 3-圈,则存在一个顶点v∈V(D),使得d++(v) ≥ λd+(v),这里λ=0.695 860…是方程在区间(0,1)上的唯一实根。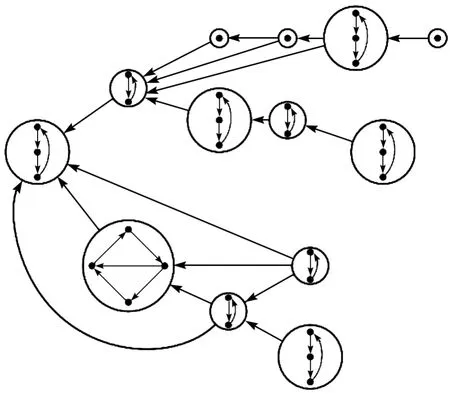
2 局部外竞赛图上顶点的二次外邻



3 局部外竞赛图的终止强分支上的二次外邻

