以数学建模为载体培养高职生数学应用能力的实践
以数学建模为载体培养高职生数学应用能力的实践

马萍


(湖州职业技术学院 机电工程分院, 浙江 湖州 313000 )
摘要:以数学建模为载体,加强高职学生数学应用能力培养,设计了“基础知识模块+选修模块”的高职数学教学内容的模块式结构及具体教学思路,并从高职数学课堂教学方法、学习过程的评价、分级考试制度、课外兴趣小组等方面进行实践与探索。
关键词:数学建模;高职数学;数学应用能力
收稿日期:2014-10-30
基金项目:浙江省教育科学2014年度规划课题“以数学建模为载体的高职学生数学应用能力培养策略研究(2014SCG412)”。
作者简介:马萍(1963-)女,浙江临海人,副教授,主要从事高职数学教学研究。
中图分类号:G172


Practice of Developing Higher Vocational College Students’ Capability
MAPing
(Faculty of Electromechanical Engineering,Huzhou Vocational and Technological College,Huzhou313000,China)
Abstract:To developing higher vocational students’ capability of Applied Mathematics, the paper, based on mathematical modeling, designs detailed teaching contents and ideas about higher vocational mathematics, including foundation and elective knowledge. Also, the teaching method of higher vocational mathematics, evaluation of learning process, grading examination system and extracurricular interest groups are considered and further explored.
Key words:mathematical modeling; mathematics in higher vocational college; mathematics application ability
近年来全国大学生数学建模竞赛在高职高专院校院校迅速发展起来,2014年浙江省有三十多所高职高专院校共128个参赛队参加了浙江赛区的比赛,数学建模活动在各大专院校的开展欣欣向荣。
数学模型(Mathematical Model)是以数学符号、数学表达式、程序、图形等工具对现实问题或实际问题的本质属性进行抽象而简洁的刻画,数学模型的建立常常需要对现实问题有比较深入细微的观察和分析,又需要灵活应用各种数学知识。所以开展数学建模活动能提高学生对数学理论知识学习的积极性和主动性,提升他们应用数学知识解决实际问题的能力,对培养学生的创新意识、探索精神以及不怕困难、团结协作、求实严谨的作风都具有十分重大的现实意义和理论意义[1]。
纵观目前高等院校对学生进行数学建模思想与方法的训练主要途径有以个两个:第一,开设数学建模课程,由于高职学制短,分配给数学课程的课时数较少,这个途径受到时间的限制;第二,将数学建模的思想和方法有机地贯穿到日常的数学课堂教学活动中,使学生在学习高职数学基础知识的同时,初步获得数学建模的知识和能力,为今后用所学的数学知识解决实际问题打下一定的基础,这是适合高职院校实际、且行之有效的方法。
本文以数学建模为载体,探索如何在数学课堂教学中加强高职学生数学应用能力培养,对历时一年多的实践进行总结,以期抛砖引玉,与同行们共勉。
1 设计“基础知识模块+选修模块”的高职数学教学内容
以数学建模为载体培养高职学生数学应用能力最重要的是将数学建模的思想和方法融入到日常高职数学教学活动中,首先应对课程内容进行优化与整合。笔者根据多年教学实践积累和调研分析,将数学教学内容与专业方面的素材紧密联系,通过课程模块的重构与整合,以适应高职各专业对大一数学基础课的动态需求。
课程结构:“数学基础平台+数学选修内容”。高职数学内容:“基础知识模块+选修模块”,其模块内容如下:
基础知识模块:函数、极限与连续;一元函数微分学;一元函数积分学;MATLAB软件。
专业选修模块:
机电类专业:常微分方程;傅里叶级数;拉普拉斯变换。
经管类专业:线性代数;概率与数理统计初步;线性规划。
计算机类专业:线性代数;离散数学;图论。
《应用数学基础》课程内容根据高职学生和专业的特点,遵循“淡化严密性、注重应用性”的原则。课堂教学中通过实际背景并结合专业引出基本概念、基本定理。微积分应用是实例分析的良好时机,如对机电类专业在函数一节教学中引入电学中常用函数:简谐波、单位阶跃函数、矩阵波函数;在导数概念教学中可以从非恒定电流的电流强度、变速直线运动瞬时速度等导入;导数计算中列举低频跨导的计算和各种变化率模型的应用:如速度与加速度、电流强度、比热计算等等;最值问题的举例中增加实际电压源最大功率计算;积分应用中分析得出整流平均值的计算方法;微分方程应用中探讨求解一阶电路的零输入响应的数学模型等等。一系列应用实例都贴近学生所学专业,也使数学课程与专业课程的衔接更为融洽,增强了学生应用数学知识解决实际问题的意识和能力。
教学过程中渗透数学建模思想,应循序渐进,从简单到复杂,逐渐渗透。可以选择与生活实际联系较密切,学生容易接受、趣味性较强并且实用的内容。如在微分方程的应用中设计如下背景材料,让学生思考:张某是嫌疑犯吗?受害者的尸体晚上19∶30发现,法医于20∶20赶到凶案现场,测得尸体温度为32.6 ℃,一小时后,当尸体即将被抬走时,测得尸体温度为31.4 ℃,室温在几个小时内始终保持在21.1 ℃。此案的最大嫌疑犯是张某,但张某声称自己是无罪的,并有证人说:“下午张某一直在办公室上班,17∶00时打了个电话,打完电话就离开了办公室。”从张某办公室到凶案现场需步行5分钟。问:(1)张某是嫌疑犯吗?(2)若张某的律师发现受害者死亡的当天下午去医院看过病,病历记录:发烧38.3 ℃,试问张某能排除在嫌疑犯之外吗[2]?
要求学生三人一组进行讨论,最后按小论文的格式(按模型假设与变量说明、模型的分析与建立、模型求解这几个方面撰写)上交,学生学习劲头较大,利用冷却过程中遵守牛顿冷却定律,即“物体冷却的速率和当时物体与介质的温度差成正比”来解决本案的问题。在小论文的撰写方面,教师课堂上通过典型的论文点评来提高学生逻辑思维能力。
课堂教学中列举数学建模实例,仅仅是学生学习数学建模思想和方法的第一步,因此在教学中举例忌大而泛,重要的是不能冲淡高等数学理论知识的学习,因为没有扎实的数学理论知识,就谈不上数学知识的应用。其次,教学中在强调重视实际应用的同时,使学生理解数学是源于现实而又高于现实的。也就是要使学生认识到数学绝不仅仅是工具,而是要从所做的数学推导和所得到的数学结论中,指出所包含的更一般、更深刻的内在规律,指出从具体问题进一步抽象化、形式化,从而上升到一般规律性认识的必要与可能[3]。
2 融入数学建模思想,编写适应高职高专学生的案例辅导材料
课程结构的改变,要求教材建设必须紧紧跟上,现有高职数学教材中与专业学习相关的应用性内容太少,而且也很落后陈旧,远远不能适应当前专业学习的需要,因此教改十分迫切地要求对教材进行重新编写,增加与各专业学习相关的应用性案例或实例,只有这样才能使学生在平时的数学学习中体会到它的实用性,也只有使教材中的应用性问题与最新的专业发展状况相联系,学生才会感受到数学的“与时俱进”[4]。因此,课题组老师在原有浙江省“十一五”重点教材《高等数学应用基础》的基础上,融入建模思想,联系专业实际收集案例并加工成教学案例,吸取国外微积分教材的优点,编写了适应高职高专学生的、以提高高职高专学生数学应用能力为目的的案例辅导材料《应用数学基础学习辅导》。
3 采取导师制方法展开课外活动,普及数学建模知识,培养数学建模兴趣
重视实践性教学环节是提高学生应用能力的策略之一。高职数学的实践性教学设计可以课内外结合,课堂上抓住数学课程中随处可见的数学模型的特点,不失时机地体现数学建模原理;课外开展导师制小组辅导。由指导老师招有兴趣的学生,组成课外兴趣小组,普及数学建模知识,培养数学建模兴趣。导师利用业余时间进行辅导,并通过建立数学建模QQ群吸引更多的学生参加,使学生的受益面不断扩大。可以将大二、大三学生与大一学生组合成学习小组,学习小组成员共同探索,形成良性循环,培养学生的自学能力。对大三有专升本需求的学生也是一个良好的复习机会。经过近一年时间学习,并利用暑期进行集中短期培训后,开展校内数学建模竞赛,从中选择一些优秀学生参加全国大学生数学建模浙江赛区的竞赛。今年湖职院学生获得了全国大学生数学建模竞赛浙江省大专组C题一等奖和三等奖,并参加了送审全国奖的论文答辩。
4 探索高职数学教学新方法,注重学习过程的评价,实施分级考试制度
信息技术手段在教学中的应用是近年来教学方法改革的重要方面。一些动态为主的教学课件,可以对黑板上难以表现的内容进行展示,有利于提高学生兴趣、加深理解。如定积分概念教学中通过问题引入新课:如何求平面图形的面积?老师先用PPT动态展示:将曲边梯形分割为四个矩形、九个矩形后,提问学生:随着分割矩形的数量越来越多,矩形面积之和与曲边梯形的面积有怎样的关系?学生就会争相回答:分割矩形个数越多,矩形面积之和就越接近曲边梯形面积;然后动态演示曲边梯形分割加细时的变化情况:13个分割点,23个分割点,63个分割点,133个分割点,143个分割点,学生非常直观地观察到随着分割点越来越多,矩形面积之和越来越接近曲边梯形的面积,从而自然而然地得出曲边梯形面积计算方法:分割—求和—求极限;接着通过同样思路探讨求变速直线运动的路程问题,定积分的微元法思想在细雨润无声中得到了理解,从而引出定积分概念。
计算机与课堂教学的整合,使传统数学教育由一支粉笔、一块黑板的课堂教学走向“屏幕教学”,由讲授型教学向创新型教学发展。用Matlab等软件做出来的部分实验结果,包括计算结果、图形等等,可以使课堂教学更加生动形象,可以使教师的讲解也更贴近学生的建模过程,可以使学生切切实实提高数据处理和数值计算的能力,从而完成数学建模、求解及结果分析的全过程,有效地激发学生学习数学的兴趣,提高学习数学的积极性,改变学生被动接受的形式。由于课时的关系课题组只安排3个共计8课时的数学实验课,分别是:实验一用数学软件做初等数学(2课时);实验二用数学软件做二次函数微积分(4课时);实验三综合实验(2课时)。
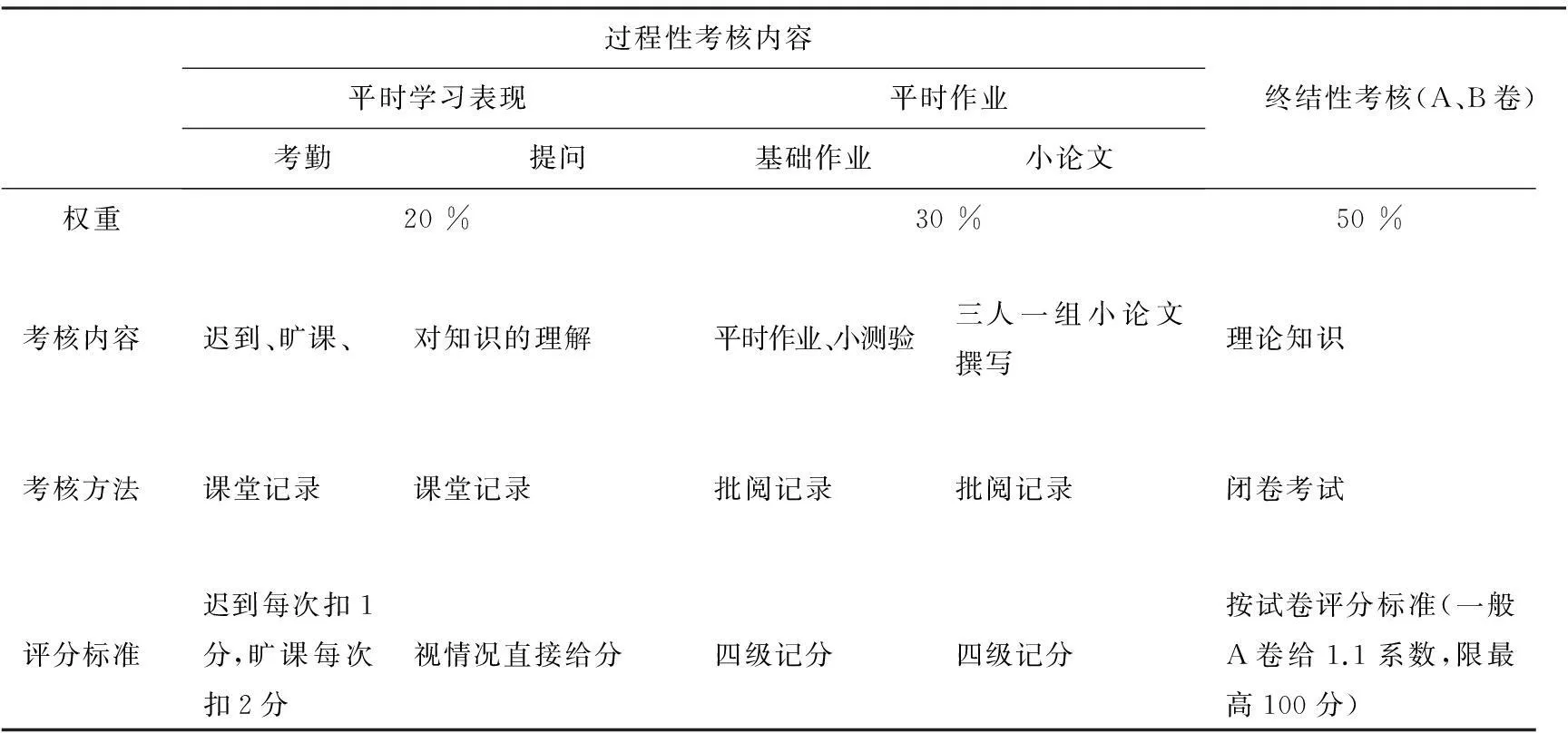
表1 课程考核方法
教学方法的创新同时也要体现在考试制度的改革上,高职学生中平时不学习,考前搞突击的不在少数。要重视学习的过程评价,弱化结果,这一点对于高职生尤其重要。课题组采取一章一小测,每节课课后或者下一节课前都针对前一节的主要知识点出一些有代表性的题目来巩固和复习,教师批改记录作为学生平时成绩之一,题型可作为期末考试复习资料。期末考试采取分级考试模式(分A级和B级),学生自主选择,考前进行选卷指导,帮助学生定位。选择A 级的学生获得相应奖励(如在总分评定上给予一定系数,并进行限最高,不超过100分);一些困难学生通过选择B 级,维护了他们本已微弱的学习信心,体现了以人为本、因材施教的教学原则,具体的考核方法如上表1所示
5 结 语
在高职数学教学中融入数学建模的思想和方法,对培养高职学生分析和解决实际问题的能力起到非常重要的作用,这是高职数学教学改革和发展的方向,无疑会成为促进高职学生可持续发展的素质教育的重要载体。高职学生数学基础差,生源类别多,有自主招生、有普高、有三校生、有3+2等等,因此高职数学教学改革任重道远,需要为之不断探索,才能达到预期效果。

参考文献:
[1] 徐志科.高职数学教改的突破口[J].职业教育研究,2007(8):100-101.
[2] 冯清.建模思想融入高等数学教学中的实践与思考[J].福建师大福清分校学报,2011(2):54-57.
[3] 吕爱玲,陆伟峰,徐兰英.从数学建模引发数学教改[J].职业,2012(3):25-26.
[4] 莫国良,吴明华.国外应用性微积分教材的特色及其启示[J].高等数学研究,2008(4):122.


