高等数学几种解题思维的探究
高等数学几种解题思维的探究

詹玉 , 徐肖丽


(商丘职业技术学院, 河南 商丘 476100)
摘要:思维的培养应体现在数学教学的各个方面,一题多解、一题多变是归纳思维、类比思维、发散思维、逆向思维在实际教学中的具体应用和表现形式。通过高等数学的一些基本实例,具体阐述了培养学生思维的方法与途径。
关键词:高等数学;解题思维;归纳思维;类比思维;发散思维;逆向思维
收稿日期:2014-09-22
作者简介:詹玉(1964-)男,河南商丘人,副教授,主要从事高等数学研究;徐肖丽(1966-)女,河南商丘人,副教授,主要从事高等数学研究。
中图分类号:G718.5


Exploration on Several Problem-solving Thinking of Advanced Mathematics
ZHANYu , XU Xiao-li
(Shangqiu Vocational and Technological College, Shangqiu476100,China)
Abstract:The thinking ability is useful in all aspects of math teaching. For example, the inductive thinking, analogical thinking, divergent thinking and reverse thinking can be applied and manifested in the conditions of one question with multi solutions or one question with multi variations. In this paper, certain methods of thinking ability will be described through some specific examples in advance mathematics.
Key words:Advanced Mathematics; problem-solving thinking; inductive thinking; analogical thinking; divergent thinking;reverse thinking
1 高等数学解题思维的研究现状及意义
在传统数学教学中,教师往往是上来就讲某个数学题目的具体解法,不去讲思维的过程,不去告诉学生老师到底是怎样想的。难道老师就一下子找到正确的思考方法了?到底怎样科学的思考问题?这是学好高等数学至关重要的问题,没有一个好的思维习惯,不会辩证思维,不会科学地思考问题,是很难学好高等数学的。
在高等数学解题中,教师通常只会想到一种解法,这样就具有很大的局限性,实际上一道题目如果从不同的角度去想,按照不同的思维方式,往往会有多种解法。对于同一题目采用不同解法与技巧,能够使学生巩固基础知识,提高解题能力,加强运算技巧,还可以使我们对所学知识间的纵横关系有所了解,同时还乐意从这些不同的解法中比较优劣,从中找出更简洁的解题途径。
一题多解可以开阔解题思路,进而提高分析问题和解决问题能力。一题多变是指当条件减弱时结论还是不是成立?或者当条件适当加强时会有什么新的结论?培养学生思维的广阔性和深刻性。
学校培养出来的学生如果缺少科学严谨的思想和广阔的思维,是无法做出优异的成绩来的。教书育人教知识,更要教思想方法。高等数学中蕴涵的数学思想以及由数学思想培养起来的思维能力和素养,将会使学生终生受益。
历史事实表明,创新能力是科技与社会发展的决定性力量。没有创造思维的人,不可能开拓进取;没有创新精神的民族,难以实现繁荣和持续发展;没有创新的时代,必将黯淡而平庸。
在高等数学教学中,充分重视归纳思维、类比思维、发散思维和逆向思维这四种解题思维能力的培养,对于提高学生解题能力和分析问题的能力,将起到至关重要的作用。
2 归纳思维探究
归纳思维是人类赖以发现真理最基本的重要思维方法。归纳是在通过对具体事物的认真分析,总结出其中的一般规律性,是从特殊到一般的抽象化思维。
在高等数学中,许多重要结果的得出,都用到了归纳思维。例如,求某函数的n阶导数,通常的方法是求出一阶、二阶、三阶导数,就可以找到规律。但有时还要求出四阶、五阶导数,然后才能归纳出n阶导数的表达式。
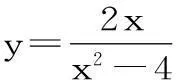
[(x+2)-1]′=(-1)(x+2)-2,
[(x+2)-1]″=[(-1)(x+2)-2]′=(-1)(-2)(x+2)-3=(-1)2·2!·(x+2)-3
[(x+2)-1]‴=[(-1)·2!·(x+2)-3]′=(-1)2·2!(-3)(x+2)-4=(-1)3·3!·(x+2)-4
……
所以[(x+2)-1](n)=(-1)n·n!·(x+2)-(n+1)
同理[(x-2)-1](n)=(-1)n·n!·(x-2)-(n+1)
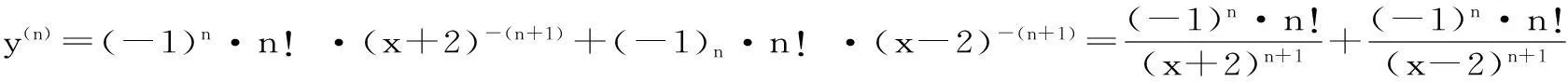
3 类比思维探究
新知识与旧知识总是有联系的,新知识建立在旧知识上,从思想方法上,从形式内容上,新旧知识都有许多类似之处,即二者具有共性。关联新旧知识是一项重要的教学内容,不仅使学生能认识问题的实质,而且使他们在运用中产生联想,得出更多的结论[1]。
类比是根据两个或两个以上的对象在某些方面相似或相同,由此及彼,从而得出它们在其他方面也可能相同或相似的推理。类比使学习节省更多的时间,联想会发现更多不同对象的共性、会使人更多的从宏观上看问题。
例如,通过对牛顿—莱布尼茨公式、格林公式、高斯公式、斯托克斯公式进行类比,发现他们有某些本质共有的规律:
若将牛顿—莱布尼茨公式:
视为:它建立了一元函数f(x)在一个区间的定积分与其“原函数”F(x)在区间边界的值之间的联系,那么通过类比,就可以将格林公式:

视为:它建立了二元函数f(x,y)在一个平面区域D上的二重积分与其“原函数”在区域边界L的曲线积分之间的联系;
就可以将高斯公式:

视为:它建立了三元函数f(x,y,z)在一个空间区域Ω上的三重积分与其“原函数” 在区域边界曲面S上的曲面积分之间的联系;
就可以将斯托克斯公式:
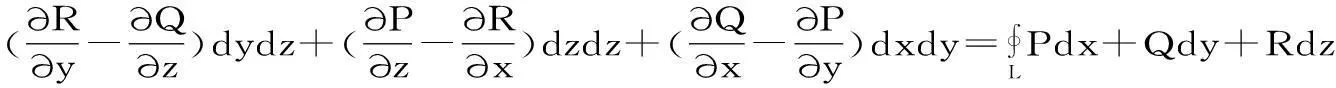
视为:它建立了三元函数f(x,y,z)在一个空间曲线S上的曲面积分与其“原函数”在区域边界曲线L上曲面积分之间的联系。
从而,可将格林公式、高斯公式、斯托克斯公式都看作牛顿—莱布尼茨公式的高维推广,从宏观上找到他们的本质共性。
教学实践证明:在学习过程中,将新知识与熟悉的旧知识进行类比,不但使学生对新知识易于接受理解,更重要的是培养、锻炼了学生的类比思维,有利于开发学生的创造力。
4 发散思维探究
所谓发散思维是指信息处理的途径灵活多变,求解的丰富多样。因此,也把发散思维称为求异思维。如,某公司在上下班时是坐电梯的高峰,员工们急忙赶路,很着急地等待,你争我抢,秩序比较乱。于是公司为了缓解着急情绪,就有人想出在等待电梯的地方安装一个穿衣镜,不少员工们很注意自己的形象,纷纷照镜,整理衣冠,于是分散了他们的注意力,问题很容易就得到了解决。
因此,在高等数学教学中,可应利用一题多解、一题多变来培养训练学生的发散思维。
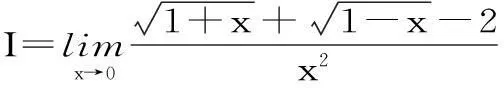
解法一:“分子有理化法”
解法二:两次用洛必达法则
解法三:用泰勒公式


通过一题多解,使得同一问题从不同角度思考,解法更加灵活了,更重要的是培养训练了发散思维。
5 逆向思维探究
逆向思维是相对于惯性思维的另一种思维形式。它的基本特点是从已有思路的反方向去思考问题。它对解放思想、开阔思路、开创新的解决问题的方向,往往能起到积极的作用。1907年的一天,在伦教火车站举行了一场“除尘器”的表演。研制者想用“除尘器”鼓起的风把尘土吹走,结果是尘土飞扬,观众们被弄得浑身上下都是土,狼狈不堪,表演失败。一位观众想,吹尘不行,吸尘行不行呢?经过试验,吸尘的方法果然可以,比起吹尘的方法要好得多。反“吹”为“吸”,思考方法跟原来正好相反,意想不到地解决了问题,所以吸尘器从此诞生了。因此, ⑴ 假如遇到某些问题顺推不行,可以考虑逆推。 ⑵ 假如遇到某些问题直接解决困难,就应想方设法间接解决。 ⑶ 正命题研究过后,研究逆命题。 ⑷ 探讨可能性发生困难时,转而探讨不可能性。

若将x视为自变量,y视为未知函数,求解此方程就困难,因为它既不是可分离变量的微分方程,也不是齐次微分方程,也不是全微分方程,而且对未知函数y来说也不是线性微分方程和伯努利方程。但是,如果利用逆向思维,即反过来将视为未知函数,视为自变量,将方程变为:

它就是未知函数x的一阶线性非齐次微分方程,从而容易求出其通解。
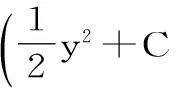
例4[2]设f(x)=x(x-1)(x-2)…(x-10000),求f′(0)
分析:若对此题直接进行求导,难上加难,几乎不可能。如果换一种角度看问题,则易于解决。比如,令g(x)=(x-1)(x-2)…(x-10000),则有f(x)=x·g(x)
因为f′(x)=[x·g(x)]′=g(x)+x·g′(x),所以f′(0)=g(0)+0·g′(0)=g(0)=10000!
另外,也可以考虑用导数定义:

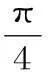




6 结 语
古人云:“授人以鱼,不如授人以渔”,因此,教的最终目的是不再教,是教给学生怎样自学。现代认知心理学家皮亚杰也认为“教育的宗旨不在于把尽可能多的东西教给学生,取得尽可能大的效果,而在于教学生怎样学习,学习发展自己,以及离校后继续发展。”这就要求在教学过程中,除了让学生掌握必要的数学知识外,引导学生如何学习也显得非常重要,在掌握学习方法的同时,培养学生的创新思维能力。
数学教学若仅仅限于具体问题教学,而不去寻找规律与方法,就偏离了数学教学的本质,学不到真正的数学思想与方法,更谈不上培养学生的创新思维能力,以及应用数学去创造性地解决实际问题了。因此包括思想方法在内的数学教学才是真正意义上的教学。
总之,教师应该在传授知识的同时,注重培养学生的思维能力。思维能力的培养,不仅可以让学生获得教材以外的思想方法,而且认识问题的深刻性、解决实际问题的能力也会大大提高,从而增强数学应用意识,解决更多的实际问题。

参考文献:
[1] 詹玉.浅谈数学教学中如何培养学生的思维能力[J].中专天地,2001(10):49-50.
[2] 杨松华,王爵禄.高等数学一题多解[M].郑州:郑州大学出版社,2002:9,22,58.
[3] 李心灿.高等数学第二版下册[M].北京:高等教育出版社,2003:368.


