“微视频”在初中数学课堂教学中应用的探索和思考

摘 要：现代教育技术已经越来越多地渗透到日常的课堂教学和学生的自主学习中，初中数学网络课程的开发应运而生；“微视频”作为网络课程开发的重点项目之一，其与课堂教学的整合走在改革的前沿；以“解一元一次方程1”为例，具体阐述了“微视频”在日常数学课堂教学中有机整合的尝试，以及由此获得的启发和思考，为后继的研究和应用提供参考.

关键词：微视频；课堂教学；整合；启发

“微视频”的开发和应用，是我们网络课程开发的重点项目之一.所谓“微视频”，目前学术界尚没有一个统一的定义，笔者界定的“微视频”，指的是时长在10分钟以内的，根据一定的教学内容设计的，供施教者辅助教学或为学习者自主探究、自主思考提供辅助平台和脚手架的能在各类终端浏览和交互的视频片段.我们初中数学微视频的制作工具主要是Camtasia Studio 7、PowerPoint和几何画板等.目前我们研究的课题是“如何将‘微视频有机地渗透于课堂教学”，从而更好地为日常的数学课堂教学服务.本文以笔者在盐城大丰送教时开设的一节研究课为例，结合本课的教学目标和重点，阐述“微视频”在数学课堂教学中的应用尝试.

一、基本情况

1.学情分析

学生来自盐城大丰市实验中学，是借班上课，因此，对学生的总体情况不是很了解.但根据进度分析可知，学生已经有了小学“解简易方程”的经验，并在此之前已经经历了“从问题到方程”的学习，知道了方程是刻画现实世界的有效工具，但上一课列出方程后并没有求出方程的解，学生有求出方程的解并彻底解决问题的欲望等.并通过侧面了解，发现大丰市实验中学的学生热爱学习，善于动脑，对数学学习有着较高的热情和信心，有扎实的数学基本功，有一定的分析、理解能力，有小组协作的基础和经历.

2.教材分析

（1）所授内容在教材中的位置

七上“4.2解一元一次方程”是学生在学习了有理数的运算、用字母表示数、整式的加减和从问题到方程等内容后来学习的，是中学数学的重要内容，也是数学中的基本运算工具.本节是有理数和整式运算的综合，是后面用方程解决问题的基础，同时也是后继学习二元一次方程组、一元一次不等式（组）及一元二次方程的基础，在整个初中教材体系中起到承前启后的作用.

（2）学习目标

①了解方程的解和解方程的概念；

②通过观察实验探究等式的基本性质，并能利用等式的基本性质解简单的方程；

③在解方程的过程中初步体会检验的作用，养成检验反思的好习惯；

④知道求方程的解就是将方程变形为x=α的形式，体会“转化”的思想方法；

⑤在学习过程中，勇于阐述自己独特的见解，学会尊重和倾听，在共同探究中提高自己发现问题、提出问题、分析问题和解决问题的能力.

（3）学习重点和难点

感悟并理解等式的基本性质，并利用等式的性质解简单的一元一次方程.

二、教学过程（有删节）

1.自觉体悟

……（省略课题导入）

体悟：

师：研究解方程之前，我们先来做一个游戏，请同学们拿出课本，你能用一根手指将其顶起来吗？（学生纷纷尝试游戏）

生1：我能.（当场展示）

师：说明我们找到了它的一个支点，即平衡点.如果换成一把直尺或铅笔，你还能吗？（学生再次尝试游戏并交流感受）

师：当笔平衡时，说明支点两边的质量相等，若设其中一边的质量是a，另一边的质量是b，则可得等式a=b.我们知道，像x+1=3这样含有未知数的等式叫方程，即方程属于等式，要研究如何解方程，我们先来看看等式到底有什么性质，因为等式的性质正是我们用来求解方程的基础和依据.

启示：此环节通过学生喜欢的游戏，引导学生感受“等式”或“平衡”就在我们的身边，数学来源于生活，渗透今天将从生活实际出发来研究“数学”中的等式问题.通过引导，帮助学生回顾等式和方程之间的关系，自然导入今天的任务是先研究等式的基本

性质.

探究任务：

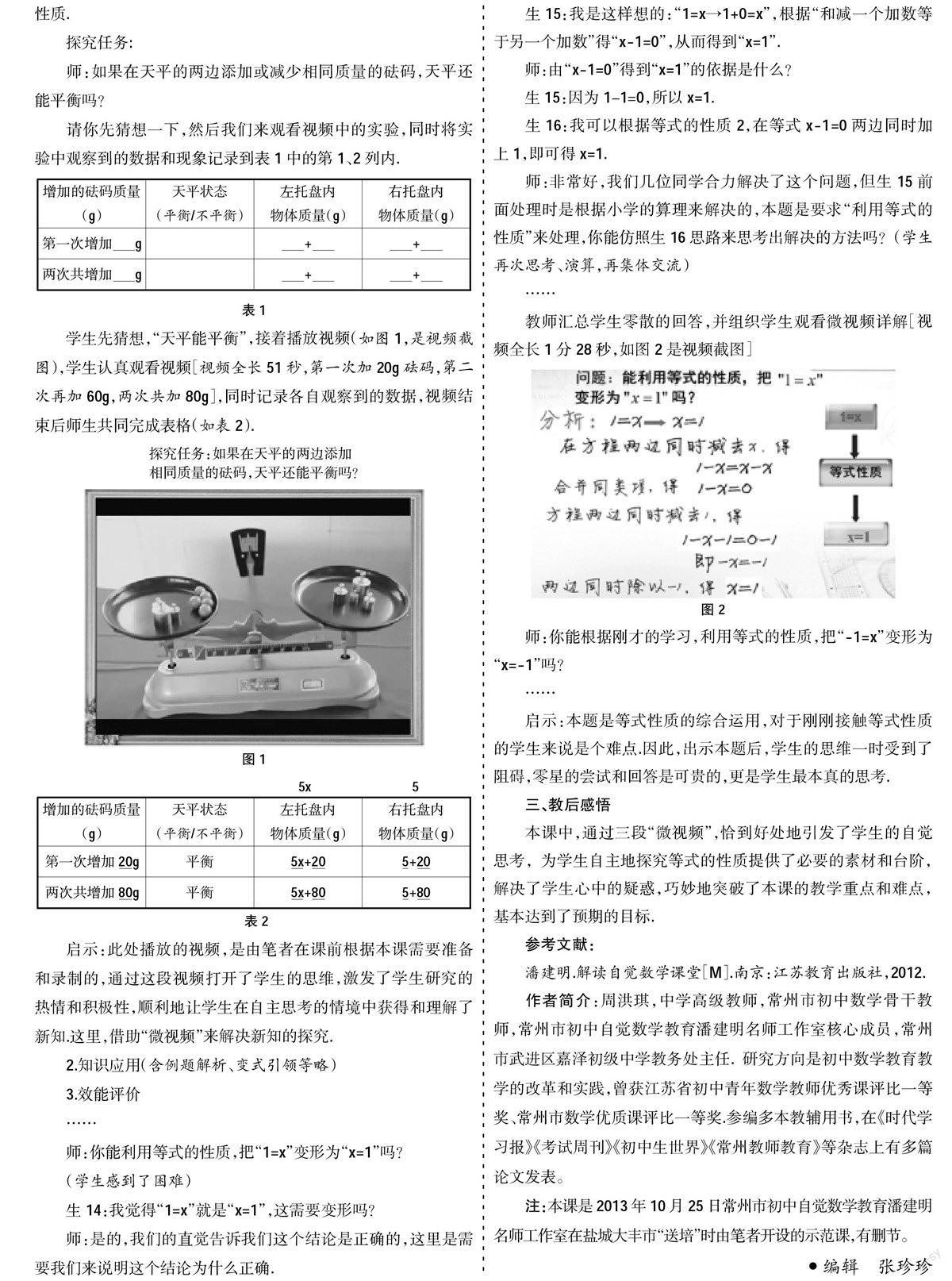
师：如果在天平的两边添加或减少相同质量的砝码，天平还能平衡吗？

请你先猜想一下，然后我们来观看视频中的实验，同时将实验中观察到的数据和现象记录到表1中的第1、2列内.

表1

学生先猜想，“天平能平衡”，接着播放视频（如图1，是视频截图），学生认真观看视频[视频全长51秒，第一次加20g砝码，第二次再加60g，两次共加80g]，同时记录各自观察到的数据，视频结束后师生共同完成表格（如表2）.

启示：此处播放的视频，是由笔者在课前根据本课需要准备和录制的，通过这段视频打开了学生的思维，激发了学生研究的热情和积极性，顺利地让学生在自主思考的情境中获得和理解了新知.这里，借助“微视频”来解决新知的探究.

2.知识应用（含例题解析、变式引领等略）

3.效能评价

……

师：你能利用等式的性质，把“1=x”变形为“x=1”吗？

（学生感到了困难）

生14：我觉得“1=x”就是“x=1”，這需要变形吗？

师：是的，我们的直觉告诉我们这个结论是正确的，这里是需要我们来说明这个结论为什么正确.

生15：我是这样想的：“1=x→1+0=x”，根据“和减一个加数等于另一个加数”得“x-1=0”，从而得到“x=1”.

师：由“x-1=0”得到“x=1”的依据是什么？

生15：因为1-1=0，所以x=1.

生16：我可以根据等式的性质2，在等式x-1=0两边同时加上1，即可得x=1.

师：非常好，我们几位同学合力解决了这个问题，但生15前面处理时是根据小学的算理来解决的，本题是要求“利用等式的性质”来处理，你能仿照生16思路来思考出解决的方法吗？（学生再次思考、演算，再集体交流）

……

教师汇总学生零散的回答，并组织学生观看微视频详解[视频全长1分28秒，如图2是视频截图]

师：你能根据刚才的学习，利用等式的性质，把“-1=x”变形为“x=-1”吗？

……

启示：本题是等式性质的综合运用，对于刚刚接触等式性质的学生来说是个难点.因此，出示本题后，学生的思维一时受到了阻碍，零星的尝试和回答是可贵的，更是学生最本真的思考.

三、教后感悟

本课中，通过三段“微视频”，恰到好处地引发了学生的自觉思考，为学生自主地探究等式的性质提供了必要的素材和台阶，解决了学生心中的疑惑，巧妙地突破了本课的教学重点和难点，基本达到了预期的目标.

参考文献：

潘建明.解读自觉数学课堂[M].南京：江苏教育出版社，2012.

作者简介：周洪琪，中学高级教师，常州市初中数学骨干教师，常州市初中自觉数学教育潘建明名师工作室核心成员，常州市武进区嘉泽初级中学教务处主任.研究方向是初中数学教育教学的改革和实践，曾获江苏省初中青年数学教师优秀课评比一等奖、常州市数学优质课评比一等奖.参编多本教辅用书，在《时代学习报》《考试周刊》《初中生世界》《常州教师教育》等杂志上有多篇论文发表。

注：本课是2013年10月25日常州市初中自觉数学教育潘建明名师工作室在盐城大丰市“送培”时由笔者开设的示范课，有删节。

编辑 张珍珍