基于几何直观的初中数学教学实践研究

彭慧秀

摘 要：几何直观是人脑对客观事物及其关系的一种直接识别或猜想的心理状态，也是一种思维方式，兼具形象思维、抽象思维两大特征。几何直观性常用于常规数学教学，能够有效培养学生运用图形语言进行交流的能力和空间想象能力，因此，加强几何直观与数学课程整合就显得十分重要。以初中数学教学为研究对象，以全等三角形和相似三角形数学知识点为实例阐明几何直观在初中数学教学中的实践应用，旨在言明几何直观性及几何直观思维在初中数学教学中的巨大作用。

关键词：初中数学；几何直观；全等三角形；相似三角形；教学实践

新课程改革提出教学新理念，要求初中数学教师教学应以学生认知发展水平和已有经验为基础，面向全体学生，注重启发式和因材施教教学方式的运用。因此，在初中数学课程教学中，老师应注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力以及模型思想等诸多能力，以此提升数学教学效率。

一、几何直观的基本含义及利用价值

所谓几何直观，指的是人脑对客观事物及其关系的一种直接识别或猜想的能力，其能够明确感受物质存在的位置关系，此时若加以正确描述，定能发现并领悟事物位置关系中的本质。几何直观与初中数学教学联系紧密，它能够巧妙地将几何数量关系转化为直观的几何基本图形，对于研究数学几何问题大有裨益。

现阶段，不少初中生的学习基础过差，数学学习功底十分薄弱，面对几何数学题更显得束手无策，因此广大初中数学老师务必要提高自身教学水平，着手培养班级学生的几何直观能力，让学生由直观得出几何基本图形，然后研究每个几何的基本图形，再把从基本图形中得出的性质综合起来，从中再找出解决问题的方法。关于几何直观用于初中生数学教学实践最大的利用价值，就是可以借助图形将抽象的概念、定理具体化、直观化，将未知转化为已知，对于学生学习能力、学习效率的提高有着重要的价值作用。

二、以全等三角形、相似三角形为例的初中数学几何直观教学实践研究

本次教学实践以程序教学法为主，旨在通过精心设置知识项目序列和强化程序这一方式，取得可观成绩，具体教学实践内容如下：

（一）以全等三角形为例的初中数学几何直观教学实践研究

1.教学内容

复习全等三角形相关内容，重点讲解全等三角形判定定理的具体应用

2.教学目标

帮助学生巩固和理解全等三角形的五种判定方法，能够熟练应用每条判断定理

3.教学步骤

（1）复习导入

师：前面我们已经学习了全等三角形的具体判定定理，主要有几种？分别有什么？哪位同学知道。

生1：SSS、SAS、ASA、AAS、HL（老师顺便板书定理具体内容）

师：这位同学回答得非常正确，那我们今天就结合具体的数学题目来复习、巩固这几种判定定理的实践应用。

（2）开放设计，复习概念

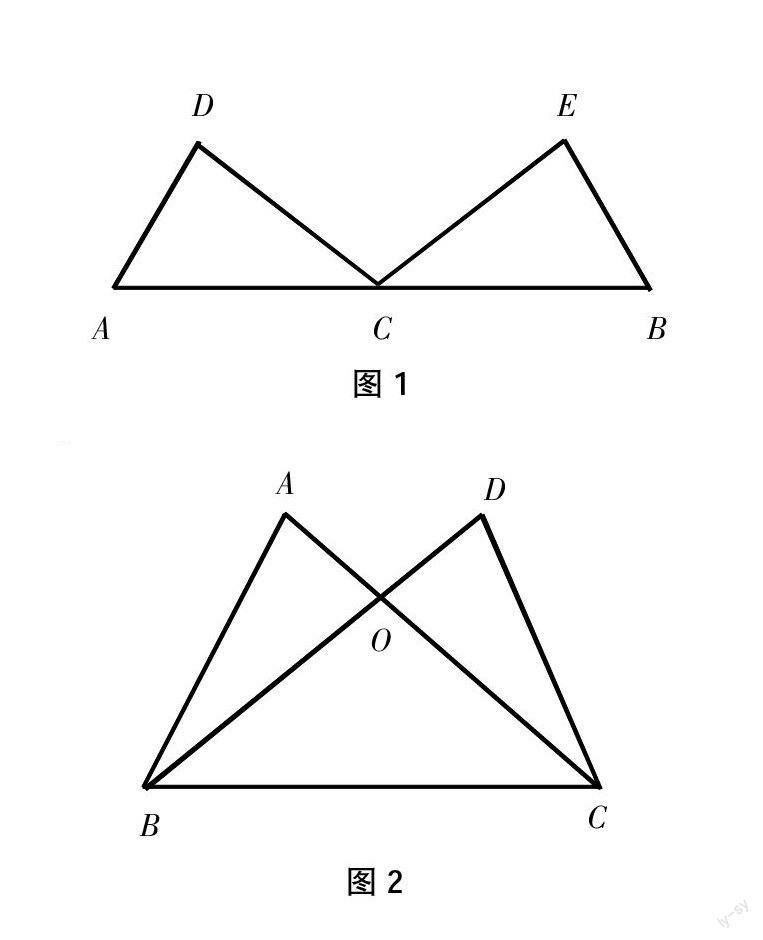
例1：如图1，点C是线段AB中点，∠A=∠B，只需添加一个条件 ，就可用三角形全等的判定“ASA”证明△ACD≌△BCE。

图1

师：大家想想，要添加什么条件才能证明两个三角形全等呢？

生2：添加∠ACD=∠BCE，构成ASA证明△ACD≌△BCE。

师：没错，那么添加什么条件可以用“SAS”证明△ACD≌△BCE呢？

生3：添加AD=BE，能夠构成SAS证明△ACD≌△BCE。

师：还可以添加什么条件？

生4：添加∠D=∠E，构成AAS证明△ACD≌△BCE。

师：能不能添加DC=EC来证明△ACD≌△BCE？

生5：不可以，因为△ACD中边AC、CD和∠A并不符合两边和夹角的关系。

设计意图：通过以上提问让学生进一步明晰这几种判定定理间边与角的关系，以防混为一潭，同时锻炼学生的发散思维能力。

（3）变式训练，攻破难点

例2：如图2，已知AB=DC，AC、DB交于点O，且AC=DB，求证：∠A=∠D。

图2

简析：此题相对来说较为简单，老师可组织学生拿两个已经准备好的三角板按图摆放，从而迅速解答问题。

变式提问1：如若把上图中的线段BC擦掉，∠A=∠D还成立吗？

生6：还成立，可用虚线连接BC进行构图，按照例题的思路解答。

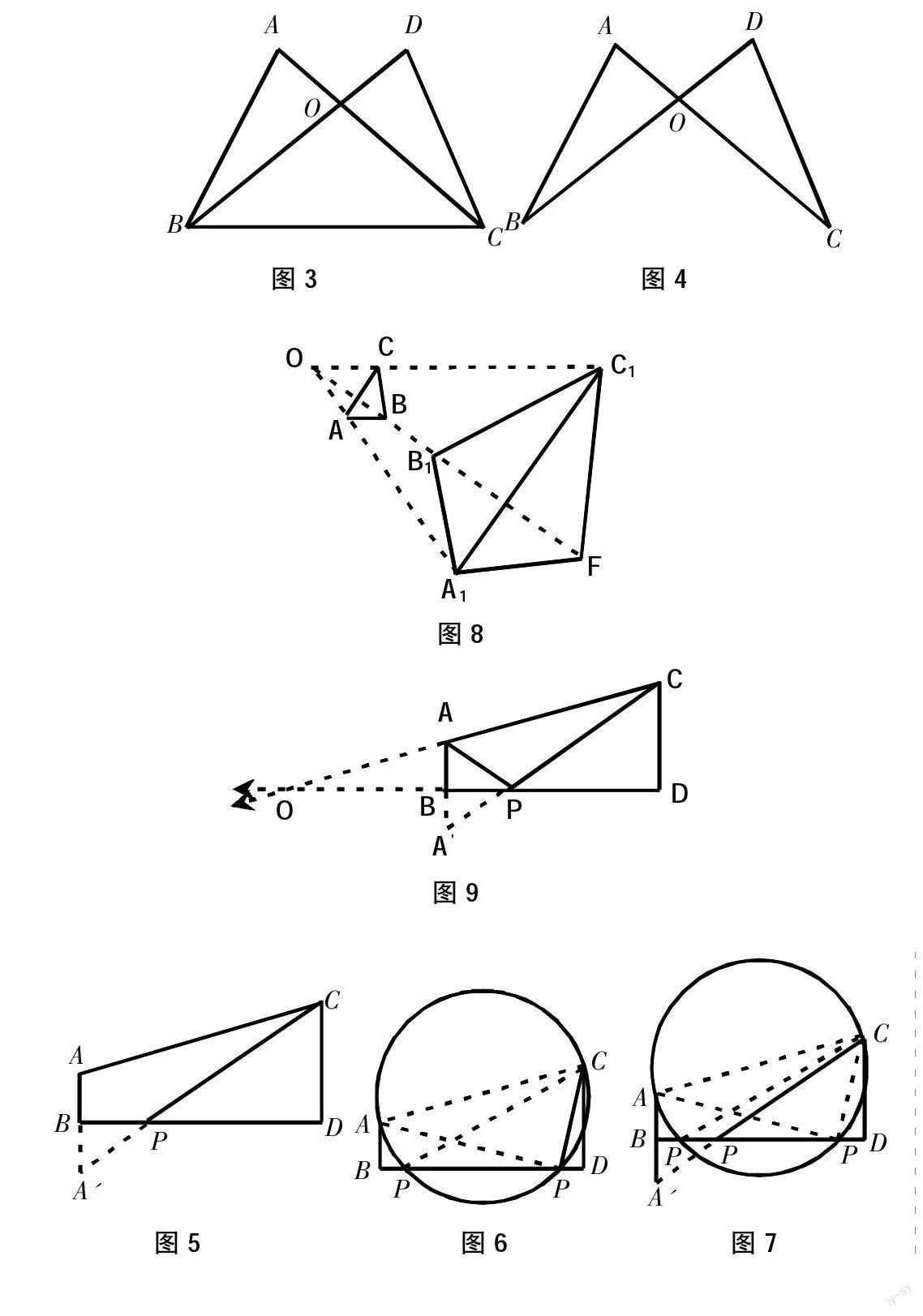
变式提问2：如图3，AB=DC、AC=DB，怎么证明∠B=∠C呢？

图3 图4

（受到例2和变式1思路的启发，学生很自然地联想到连接AD，难点得以攻破）

生7：连接AD，证明△BAD≌△CDA。

变式提问3：如图4，AB=DC，AC=DB，你能猜想出AD与BC的位置关系吗？

（这个时候学生激情高涨，求知欲完全被调动起来，热情地积极参加讨论，数学思维都有了深度和广度）

设计意图：为展现教学的层次性，笔者以例2和变式1为铺垫，由浅至深、步步迈进，有效的追问解决了题目中的难点，学生的几何直观思维也得到进一步升华。

4.小结

全等三角形数学问题的解答需要几何图形的支撑，只有站在几何图形的基础上才能真正了解到数学题目中的微妙关系，从而正确解答几何数学问题。

（二）以相似三角形为例的初中数学几何直观教学实践研究

1.教学内容

以相似三角形为中心研究对象，讲解相似三角形多解问题和位似概念，顺带运用几何画板这一工具，有效提升学生的几何直观能力，锻炼学生几何直观思维。

2.教学目标

帮助学生贯彻理解相似三角形多解问题和位似概念，拓宽几何直观思维之宽度，呈现数学问题之本质。

3.教学步骤

（1）讲解相似三角形多解问题

在相似三角形的教学过程中，常会遇到因对应关系未确定而分类讨论的现象。解题策略主要是由假定的对应关系得到成比例线段，随即求出线段的长。但如果从存在性加以说明，也许会取得可观成效。

例3：如图5，已知AB⊥BD，垂足为B，CD⊥BD，垂足为D，AB=4，CD=6，BD=14，请问：在BD上是否存在点P，使C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似？如果存在，计算出P的位置；如果不存在，请说明理由。

待求出后，再从存在入手，借助几何直观性让学生看到点的存在性，通过分析得到此作图方法：①由于AB∥CD，所以利用轴对称，作点A关于直線BD的对称点A′，连接CA′，交BD于点P，则P为所求（如图5）。

图5 图6 图7

②由于△APB∽△PCD，所以∠APB=∠PCD。又∠PCD+∠CPD=90°，所以∠APB+∠CPD=90°，从∠APC=90°，再利用“直径所对的圆周角是直角”，可以AC为直径作圆，交BD于点P（如图6）。待学生弄清后，再拖动CD，观察满足要求的点P的个数变化，再归纳总结，使学生能够快速且准确的判断点P的个数（图7），既锻炼了学生的几何直观能力，同时还拓宽了思维含量。

（2）位似概念，揭露概念本质

位似变换是相似变换的一种特例，解读此概念时要注意两个图形相似、对应定点的连线交于一点、对应边互相平行这三个要点，此处特举反例做以说明：

反例1：如图8，AC⊥OB，△A1FC1与△ABC关于O点位似，△A1B1C1与△A1FC1关于直线A1C1对称，从而△A1B1C∽△ABC，且满足AA1、BB1、CC1相较于点O，但是△A1B1C和△ABC不是位似的。

反例2：如图9，AB⊥BD，CD⊥BD，A、A′关于直线BD对称，连接CA′交BD于点P，从而△ABP∽△CDP，且满足AB∥CD，BP与DP共线，还满足CA、DB相较于点O，但是△ABP与△CDP不是位似的。

以上两个反例从反面视角揭露了位似概念的本质，对学生理解几何问题大有裨益，加之应用了几何画板这一工具，不仅加快了整个解题速率，而且缩短了解题用时。

4.小结

相似三角形多解问题和位似概念的理解需要借助几何图像来言明，不仅加快了解题速度，而且解题正确率也相对较高。

总之，几何直观性在全等三角形、相似三角形的教学中得以充分展现，而且全等三角形和相似三角形的解题难度也在几何直观性的帮助下有所降低，课堂教学质量也得到极大地提升。

总的来说，于初中数学教学中培养学生的几何直观能力是极为有益的，单从上文所列举的全等三角形、相似三角形两大实例便可看出初中数学教学需要几何直观能力的支持，所以初中数学老师务必要重视数学几何直观性教育的实质化进程，落实到实处，让初中生的几何直观能力在课堂教学和课后实践中得以培育。

参考文献：

[1]孙启进.盲校数学直观性教学研究[D].聊城大学，2014.

[2]孟祥文.基于超级画板的初中数学直观性教学研究[D]. 鲁东大学，2014.

[3]冉启明.直观性原则在初中数学教学中的应用[J].才智， 2009（30）.

编辑 鲁翠红