中立型时滞反馈扭转控制系统的稳定性分析*

刘铭 徐晓峰 张春蕊

（东北林业大学理学院，哈尔滨 150040）

中立型时滞反馈扭转控制系统的稳定性分析*

刘铭 徐晓峰 张春蕊†

（东北林业大学理学院，哈尔滨 150040）

研究了中立型时滞动力吸振器抑制扭转系统的振动问题.针对一类强迫扭转振动系统，采用动力系统的稳定性理论分析了动力吸振器与扭转振动系统的稳定性问题，以时滞为参数，分别得到了动力吸振器与扭转振动系统的稳定区域，并研究时滞变化时动力吸振器对于主振动系统振动的吸收效果，通过与时滞动力吸振器对比，得到了更大的吸振器和减振系统时滞稳定工作区域，通过数值模拟验证了结论的正确性.

扭转振动，中立型，动力吸振器，稳定性，减振

引言

旋转机械设备在航空、航天、车辆、船舶、机械、建筑等工程领域应用十分广泛，其核心部件是转子系统.转子系统在周期性激振力矩的作用下会产生扭转振动，使得轴系零件磨损加剧、噪声剧增，甚至会发生断轴等事故，后果非常严重.为了安全生产，需要对转子系统的扭转振动加以抑制，由于设计简单和实用性强，采用动力吸振器减振受到了众多学者的广泛关注［1-6］.传统的动力吸振器一般都不考虑时滞的作用，但实际上，对于机械系统采用主动控制后，传感器信号的采集和传输、控制器的计算、作动器的作动过程等，均会带来难以避免的时滞效应，有时尽管时滞量很小，却会影响到整个系统的稳定性和控制性能，是不容忽视的.

利用时滞效应抑制机械系统的振动是一门新兴的技术，在传统动力吸振器的基础上引进一个带有时滞的部分状态反馈，可以增大减振的频率范围，而且在某些情况下通过实时调节，可以将主系统的振动完全吸收.美国学者Olgac最早提出时滞线性动力吸振器，通过调整反馈增益系数和时滞量来达到减小主系统振动的目的［7］.Hosek等研究了采用离心摆式的时滞共振器来抑制扭转系统的振动问题，研究结果表明，通过调整反馈增益系数和时滞量可以很好的抑制主振动系统的扭转振动［8］.徐鉴和赵艳影等在时滞动力吸振器方面做出了大量研究［9-11］，赵艳影等利用稳定性切换的方法，研究了扭转动力系统的时滞减振问题，得到了很好的结果［12］.

尽管在理论研究方面表明时滞动力吸振器对主系统的振动具有很好的减振效果，但是找到合适的时滞量和反馈增益却并不容易，原因在于时滞量的可调节范围比较小，工程中实践起来比较困难.本文采用中立型时滞动力吸振器抑制扭转系统的振动，通过引入中立型反馈可以扩大时滞量的可调节范围，提高动力吸振器的实用性.

1 力学模型

在文献［3］和［12］的模型基础上可以得到，采用中立型时滞动力吸振器抑制线性强迫扭转振动系统的集中质量模型如图1所示.

图1所示振动系统的运动微分方程为：

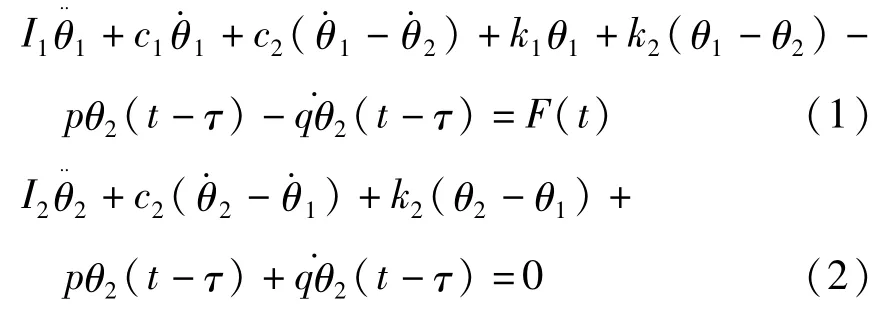
其中，θ1和θ2分别为主系统和吸振器的扭转角位移，I1和I2分别为主系统和吸振器的质量惯性矩，c1和c2分别为主系统和吸振器的线性阻尼系数，k1和k2分别为主系统和吸振器的线性弹簧的刚度系数，为中立型时滞反馈控制项，τ为时滞，p＞0，q＞0为反馈增益系数，F（t）＝Acosω0t为外激励项.

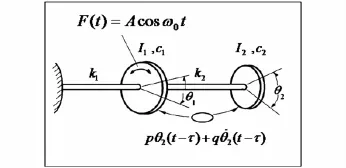
图1 中立型时滞动力吸振器抑制扭转振动系统Fig.1 A model of vibrating suppression for torsional vibrating system with delayed vibration absorber of neutral

2 中立型时滞动力吸振器的稳定性分析

首先研究中立型时滞动力吸振器的稳定性问题.图1所示的减振系统中的中立型时滞动力吸振器运动方程为：

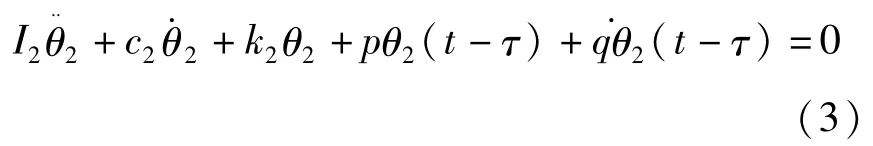
其特征方程为：

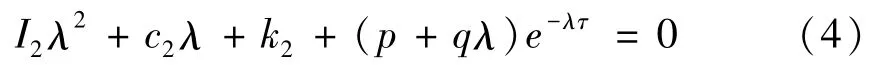
显然，当τ＝0时，特征方程（4）的两个根都具有负实部.假设λ＝±iβ（β＞0）为方程（4）的根，代入（4）并分离实虚部得

两端平方相加可得

可知，若p＞k2，记

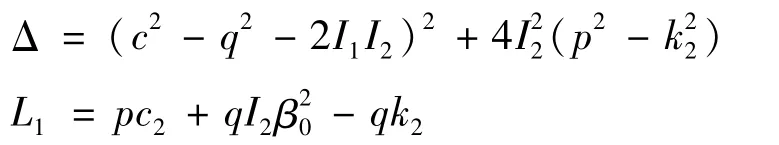
则当τ＝τj时，特征方程（4）有唯一一对纯虚根±iβ0，其中

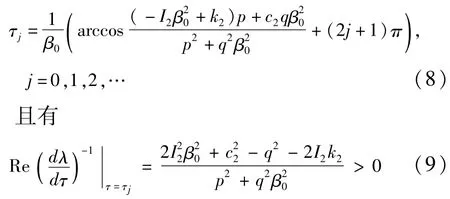
因为，当动力吸振器的固有频率与外激励的频率相等时，动力吸振器会发生共振，将外激励输入到振动系统的能量全部吸收，从而使主系统保持不振.因此，要想达到最佳的减振效果，需要使β0＝ω0，则两个反馈增益系数需要满足

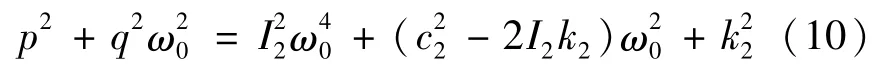
此时，动力吸振器只有一个固有频率ω0，且时滞稳定区域为τ∈［0，τ0）.

3 减振系统的稳定性分析

为了保证动力吸振器稳定工作时整个减振系统是稳定的，还需要研究整个减振系统的稳定性问题.减振系统（1）和（2）的特征方程为

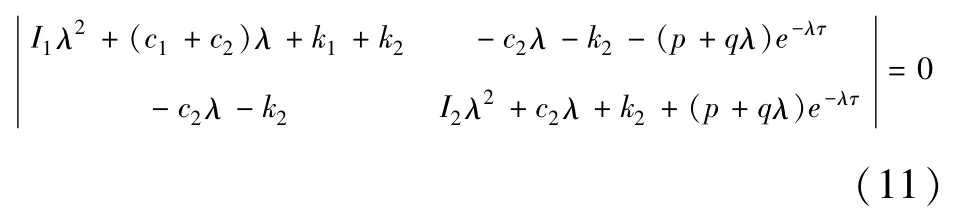
当τ＝0时，特征方程（11）化为

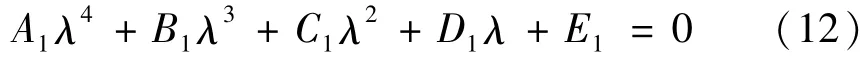
其中，

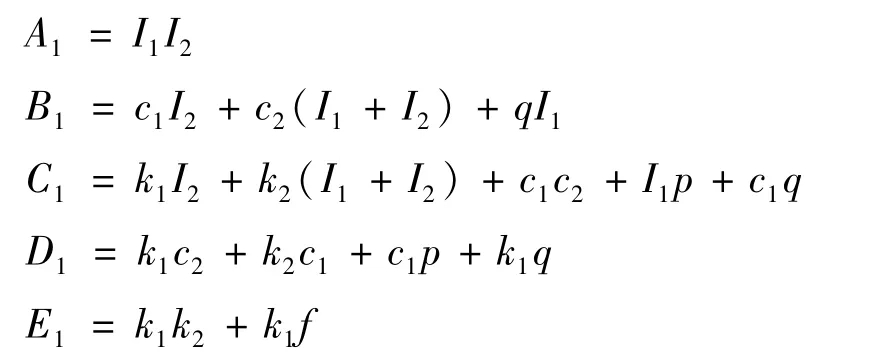
由于模型中所有参数都是正的，由Routh-Hurwitz准则知，方程（12）所有根都具有负实部的充分必要条件为

假设λ＝±iβ（β＞0）是特征方程（11）的一对纯虚根，代入方程（11）并分离实虚部得

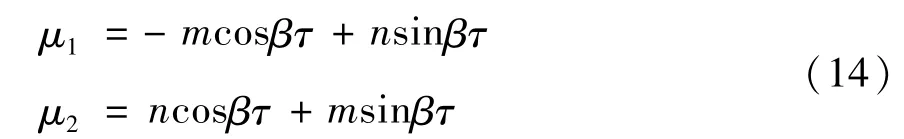
其中，

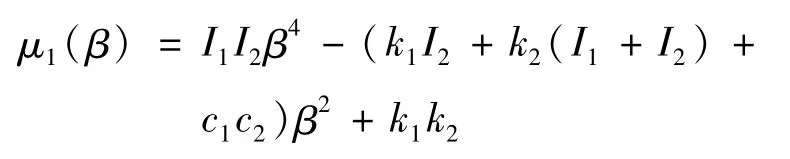
显然，若以β2为变量，方程（15）两端对β2求导可得

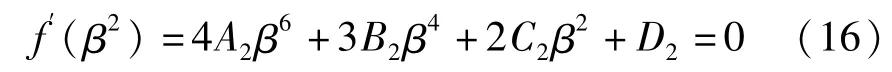
则当p＞k2时，方程（15）具有唯一正根的充分必要条件为以下两个条件之一成立

①方程（16）没有三个互异实根；

②方程（16）具有三个互异实根r1＜r2＜r3，且满足r2≤0，或f′（r2）＜0，或r2＞0，f′（r2）＞0，f′（r3）＞0.

假设方程（15）具有唯一正根β*，记

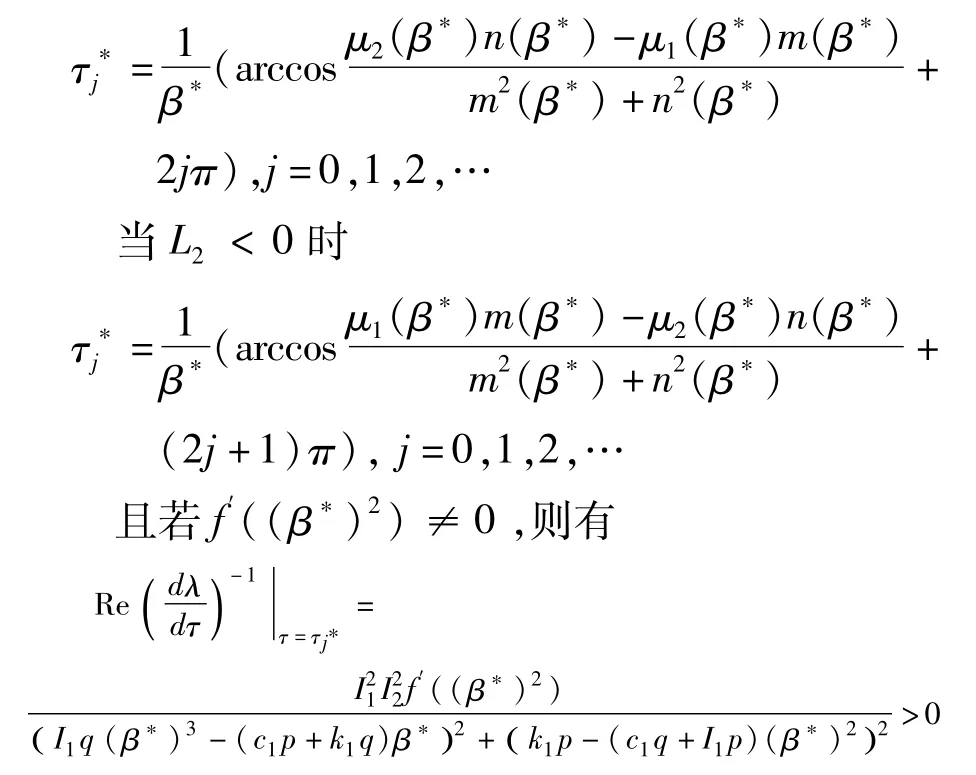
此时，减振系统只有一个固有频率β*，且时滞稳定区域为τ∈［0，）.若τ0＜，即整个减振系统的稳定性区域比中立型动力吸振器的稳定性区域范围大，则当反馈增益系数p，q满足条件（10）时，将时滞τ调节到其临界稳定值τ0时，可以将主系统的振动全部消除，并且能够保证整个减振系统是在稳定的状态下工作.

4 数值模拟

下面进行数值模拟验证结论的正确性，为说明中立型时滞动力吸振器的优越性，将系统参数取成与文献［12］中相同，即I1＝I2＝0.04（kgm2），c1＝c2＝0.20（Nms/rad），k1＝1.00（Nm/rad），k2＝3.00（Nm/rad），F（t）＝0.10cos（15.70t）（Nm），初始条件也取成与文献［12］中相同，即θ1（0）＝θ2（0）＝0（rad），（0）＝（0）＝0.01（rad/s）.在文献［12］中，作者通过研究得出结论，为使动力吸振器能将外激励输入到主系统的能量全部吸收，保证主系统不振动，需取反馈增益系数gc＝7.76（Nm/rad），此时减振器的时滞稳定工作区间为τ∈［0，0.03）（s），整个减振系统的时滞稳定工作区间为τ∈［0，0.1）（s）.

依据本文的研究，为使中立型动力吸振器能将外激励输入到主系统的能量全部吸收，保证主系统不振动，需取反馈增益系数p，q满足条件（10），不妨取p＝3.5（Nm/rad），q＝0.4257（Nms/rad），可以验证，此时吸振器只有一个固有频率ω0＝15.7（rad/s），减振系统只有一个固有频率5.2195（rad/s），而吸振器的时滞稳定工作区间为τ∈［0，0.0967）（s），整个减振系统的时滞稳定工作区间为τ∈［0，0.4699）（s）.通过对比可以发现，加入中立型反馈控制可以同时增大吸振器和减振系统的时滞稳定工作区间，下面给出具体的数值模拟结果，为书写方便，省略p，q，τ相应的单位.

图2是减振系统在不存在反馈时的时间历程响应曲线（p＝0，q＝0），对应减振器的物理参数是不可调节的，相当于被动吸振器.此时主系统扭转振动的振幅为0.009rad，吸振器扭转振动的振幅为0.005rad.

图3是减振系统存在中立型反馈但反馈控制不存在时滞的时间历程响应曲线（p＝3.5，q＝0.4257，τ＝0），此时主系统振动的振幅由0.009rad减小到0.008rad，减振器扭转振动的振幅也由0.005rad减小到0.003rad，从而证明主动控制比被动控制具有更好的效果.

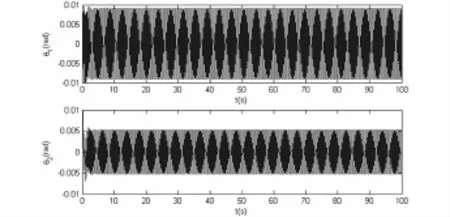
图2 减振系统的时间历程响应曲线p＝0，q＝0Fig.2 Time history response curves of the vibrating system when p＝0 and q＝0

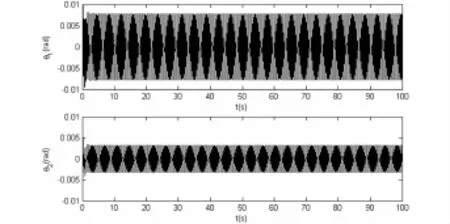
图3 减振系统的时间历程响应曲线p＝3.5，q＝0.4257，τ＝0Fig.3 Time history response curves of the vibrating system when p＝3.5，q＝0.4257 and τ＝0

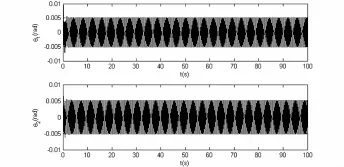
图4 减振系统的时间历程响应曲线p＝3.5，q＝0.4257，τ＝0.05Fig.4 Time history response curves of the vibrating system when p＝3.5，q＝0.4257 and τ＝0.05

图4 是减振系统存在中立型时滞反馈的时间历程响应曲线（p＝3.5，q＝0.4257，τ＝0.05），此时主系统扭转振动的振幅由0.008 rad减小到0.005 rad，而减振器扭转振动的振幅又由0.003 rad增大到0.005 rad.

图5是p＝3.5，q＝0.4257，τ＝τ0＝0.0967时减振系统的时间历程响应曲线，此时中立型动力吸振器与外激励发生共振，将外激励输入到主系统的能量全部吸收，从而将主系统扭转振动的振幅减小为0 rad.

图6是p＝3.5，q＝0.4257，τ0＝0.0967＜τ＝0.45＜＝0.4699时减振系统的时间历程响应曲线，此时主系统扭转振动的振幅为0.008 rad，中立型动力吸振器仍然在稳定工作.

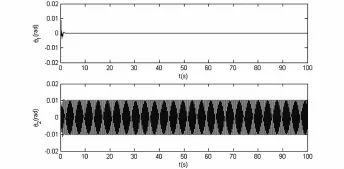
图5 减振系统的时间历程响应曲线p＝3.5，q＝0.4257，τ＝0.0967Fig.5 Time history response curves of the vibrating system when p＝3.5，q＝0.4257 and τ＝0.0967

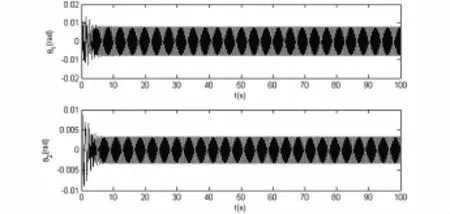
图6 减振系统的时间历程响应曲线p＝3.5，q＝0.4257，τ＝0.45Fig.6 Time history response curves of the vibrating system when p＝3.5，q＝0.4257 and τ＝0.45

5 结论

本文主要研究了采用中立型时滞动力吸振器来控制扭转振动系统的振动问题.利用稳定性理论研究了吸振器和减振系统的稳定性问题，得到的主要结论如下：

（1）对于时滞动力吸振器，要使主系统的振动被完全吸收，反馈增益系数的取值是唯一确定的，不可调节.而中立型吸振器要将主系统的振动完全吸收，两个反馈增益系数是可以调节的，取值更加灵活.

（2）通过与时滞动力吸振器对比可以发现，对于相同的系统参数和初值条件，采用中立型动力吸振器可以使吸振器的稳定工作区域扩大3倍以上，使减振系统的稳定工作区域扩大4倍以上.另外，适当调节两个反馈增益系数的取值，还可以将吸振器和减振系统稳定区域进一步扩大.

1 Muneharu S，Nobuo T，Dong H N.Torsional vibration suppression by wave-absorption control with imaginary system.Journal of Sound and Vibration，2004，270（1-2）：657～672

2 Kim T C，Rook T E，Singh R.Effect of nonlinear impact damping on the frequency response of a torsional system with clearance.Journal of Sound and Vibration，2005，281（3-5）：995～1021

3 EI-Bassiouny A F.Vibration and chaos control of non-linear torsional vibrating systems.Physica A：Statistical Mechanics and its Applications，2006，366：167～186

4 Al-Bedoor，Moustafa K A，Al-Hussain K M.Dual dynamic absorber for the torsional vibrations of synchronous motordriven compressors.Journal of Sound and Vibration，1999，220（4）：729～748

5 Lee C T，Shaw S W，Coppola V T.A subharmonic vibration absorber for rotating machinery.ASME Journal of Vibration and Acoustics，1997，119（4）：590～595

6 Chao C P，Shaw S W.The dynamic response of multiple pairs of subharmonic torsional vibration absorbers.Journal of Sound and Vibration，2000，231（2）：411～431

7 Olgac N，Holm-Hansen B T.A novel active vibration absorption technique：delayed resonator.Journal of Sound and Vibration，1996，176（1）：93～104

8 Hosek M，Elmali H，Olgac N.A tunable torsional vibration absorber：the centrifugal delayed resonator.Journal of Sound and Vibration，1997，205（2）：151～165

9 赵艳影，徐鉴.时滞非线性动力吸振器的减振机理，力学学报，2008，48（1）：98～106页（Zhao Y Y，Xu J.Mechanism analysis of delayed nonlinear vibration absorber.Chinese Journal of Theoretical and Applied Mechanics，2008，48（1）：98～106（in Chinese））

10 赵艳影，徐鉴.利用时滞反馈控制自参数振动系统的振动.力学学报，2011，43（5）：894～904（Zhao Y Y，Xu J.Using the delayed feedback to control the vibration of the auto-parametric dynamical system.Chinese Journal of Theoretical and Applied Mechanics，2011，43（5）：894～904（in Chinese））

11 赵艳影，李昌爱.时滞反馈控制扭转振动系统的振动.物理学报，2011，60（11）：1～9（Zhao Y Y，Li C A.The delayed feedback control to suppress the vibration in a torsional vibrating system.ACTA Physica Sinica，2011，60（11）：1～9（in Chinese））

12 赵艳影，李昌爱.时滞动力吸振器抑制扭转系统的振动.动力学与控制学报，2013，11（1）：36～41（Zhao Y Y，Li C A.Vibration suppression of torsional vibration system by using the delayed vibration absorber.Journal of Dynamics and Control，2013，11（1）：36～41（in Chinese））

Received 5 January 2015，revised 15 February 2015.

*The project supported by the Fundamental Research Funds for the Central Universities（2572014BB16）

†Corresponding author E-mail：math@nefu.edu.cn

STABILITY ANALYSIS OF DELAYED TORSIONAL VIBRATION SYSTEM OF NEUTRAL TYPE*

Liu Ming Xu Xiaofeng Zhang Chunrui†
（School of Science，Northeast Forestry University，Harbin 150040，China）

In this paper，the vibration suppression of torsional vibrating system is investigated through the delayed vibration absorber of neutral type.The stability theory of dynamic system was applied to study the stability of the neutral delayed vibration absorber and the torsional vibrating system，and their stable regions were obtained，respectively，by taking time delay as a parameter.Moreover，The absorbing effect of dynamic vibration absorber with the delay changing was obtained.It is shown that the stable region of the vibration absorber and vibration reduction system became larger when compared with the general delayed vibration absorber.Finally，the numerical simulations were also carried out to verify the analytic results.

torsional vibration，neutral type，vibration absorber，stability，vibration suppression

10.6052/1672-6553-2015-008

2015-01-05收到第1稿，2015-02-15收到修改稿.

*中央高校基本科研业务费专项资金项目（2572014BB16）

†通讯作者E-mail：math@nefu.edu.cn