不同脱层位置下脱层屈曲梁振动实验研究*
陈得良付钦陈昌萍
(1.长沙理工大学土木与建筑学院,长沙 410014)(2.深圳市路桥建设集团有限公司,深圳 518024)(3.厦门理工学院土木与建筑学院,厦门 361024)
不同脱层位置下脱层屈曲梁振动实验研究*
陈得良1†付钦2陈昌萍3
(1.长沙理工大学土木与建筑学院,长沙 410014)(2.深圳市路桥建设集团有限公司,深圳 518024)(3.厦门理工学院土木与建筑学院,厦门 361024)
通过实验对一端固定一端夹支脱层屈曲梁在轴向周期激励作用下的非线性动力响应进行了实验研究.利用位移时间历程图,相图和频谱图,对多组不同脱层位置下脱层屈曲梁的非线性动力响应进行了分析.实验表明脱层梁结构存在倍周期以及混沌运动等非线性动力学行为.同时实验还表明,在相同的脱层长度下,脱层位置对脱层梁的动力学特性有明显影响,即脱层区域中心越靠近梁结构的中心位置,脱层梁的一阶自然频率越低,且越容易在较低的激励频率和激励荷载下发生周期分叉和混沌等行为.
脱层屈曲梁,实验,参数振动,脱层位置,非线性动力响应
引言
梁结构由于结构形式简单,受力明确而在工程领域得到了广泛应用,其在工程应用中所表现出的各种非线性行为引起了许多学者的关注.1951年Burgreen[1]发现屈曲梁结构的自然频率与系统的振幅有关,具有明显的非线性特征,其相关试验也证明了该结论.此后许多学者[2-11]对屈曲梁的其它非线性动力学特性如跳跃,周期运动,多周期运动和混沌等行为也进行了研究.相关的理论和试验研究表明,完整梁结构存在丰富的非线性动力学行为.
近年来,为满足工程结构寿命和稳定性提高的需要,各种高性能材料如复合材料结构等在工程中得到了大量的应用.然而复合材料梁结构在使用过程中总存在各种形式的缺陷,如脱层缺陷.这些脱层缺陷的存在将使的结构静力和动力学性能出现不可预知的改变.试验表明[12]在动荷载作用下初始缺陷的存在和进一步失效将显著改变复合材料结构的动力特性和动力响应行为,因此对具有缺陷(脱层)结构的动力特性有一个清晰的了解显得十分重要.然而对脱层梁结构,由于脱层区域位移不连续而导致的复杂性,因此目前研究[13-17]主要探讨的是脱层位置、长度和铺层材料等参数对脱层梁的静力,线性自由振动和非线性自由振动问题的影响.而对脱层梁结构的其它非线性动力学特性如分叉、混沌等行为几乎没有关注,更未见从实验方面对脱层梁非线性动力行为进行研究.
为进一步拓展脱层的研究领域和范围,本文将利用相关实验对不同脱层位置下脱层梁的非线性动力学特性如周期,倍周期以及混沌等行为进行实验研究.
1 实验实施
本次实验所采用脱层梁试件如图1所示,其中Ⅱ和Ⅲ区是脱层区(未粘结区),Ⅰ和Ⅳ区是未脱层区域(粘结部分).脱层试件通过环氧树脂由两片相同的304不锈钢片粘结而成,但脱层区不粘结(保持分离).图中l表示脱层梁的有效安装长度,l1表示脱层区域中心位置距离梁左侧固定端距离.脱层的相对位置用比值l1/l或(l-l1)/l描述.传感器对称布置于脱层区域的中心位置两侧.脱层梁的有效安装尺寸均为472mm×20mm×1mm.试验中脱层梁的一端通过锚固在地基上钢结构固定,另一端则连接于固定地基上的电动激振器上.
试验系统由脱层梁,激励系统,信号采集和分析系统四部分组成.试验过程主要由三步组成.首先,测定脱层屈曲梁试件第一阶自然频率;然后利用激振系统在所测定的第一阶频率附近以不同的激励频率进行激振,识别能使发现脱层梁产生非线性振动行为的相应外激励频率.最后,在所得到的外激励频率下,保持外激励频率不变并使外激励电压由零逐步增大对脱层梁进行激振,以研究脱层梁其他非线性动力学特性.

图1 脱层梁试件示意图Fig.1 Sketch of a delaminated beam specimen
2 试验结果与分析
2.1 脱层位置对脱层屈曲梁一阶频率的影响
根据脱层位置的不同将脱层梁试件分成5组.各组脱层梁试件脱层长度均相同,其与脱层梁长度的比值均为0.3.每组脱层梁的频率采用锤击法得到.其一阶频率与脱层位置的关系如表1所示.
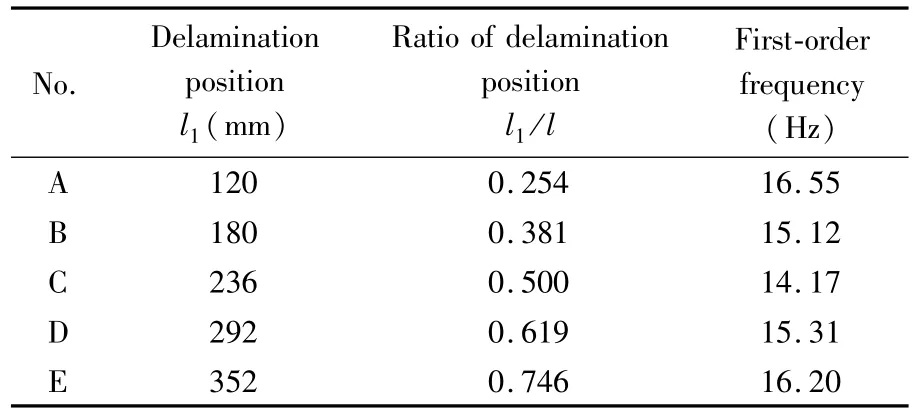
表1 不同脱层位置下脱层梁的一阶频率Table 1 First-order frequency of the delaminated beam with different delamination positions
从表1可知,当脱层区域的中心位置越靠近脱层梁的中心位置,脱层梁的一阶频率越低.当脱层区域中心位置距固定支撑端和夹支端具有的比值即l1/l=(l-l1)/l时,脱层靠近固定支撑端的频率要稍大于脱层靠近夹支端的频率.
2.2 不同脱层位置下脱层梁的非线性动力响应
实验中发现从脱层区域两侧的传感器获得数据经分析判断后具有相同的动力学特性,因此在后续分析中只采用其中一个传感器的数据进行研究.研究中利用位移时间历程图,相图和频谱图来判定脱层梁的非线性动力学行为.
(1) 情况A时非线性动力响应
当脱层区域中心离固支端l1/l=0.254时,脱层梁在不同外激励电压下的非线性动力响应如图2-6所示.实验观察到,当激励电压较小时,脱层屈曲梁基本保持静止状态,当激励电压增大到一定值时,梁才会才出现明显的振动行为.图2是激励电压为0.3V时的周期运动.当继续增大激励电压并达到2.7V时,脱层梁将会出现如图3所示的两倍周期运动.进一步增大电压,脱层梁的振动将变得更为剧烈,并伴随着不规则的噪音产生.当激励电压达到4.3V时,脱层屈曲梁将会出现如图4所示的混沌行为,此时系统的频谱是连续的,脱层梁的振动更为剧烈,脱层两部分保持紧密接触并一起振动,脱层区域为正弦状模态,振动时伴有嘈杂的噪音.当在此基础上继续增大激励电压,脱层将会相继出现两倍周期运动、混沌运动等非线性现象,分别如图5-6所示.
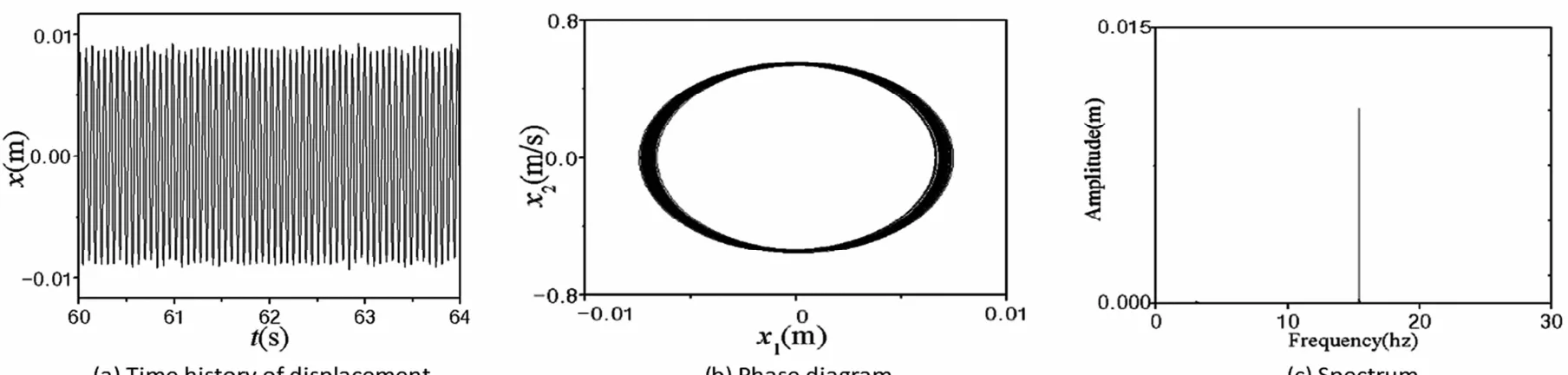
图2 激励电压0.3V时的周期运动Fig.2 The periodic motion under a excitation voltage of 0.3V
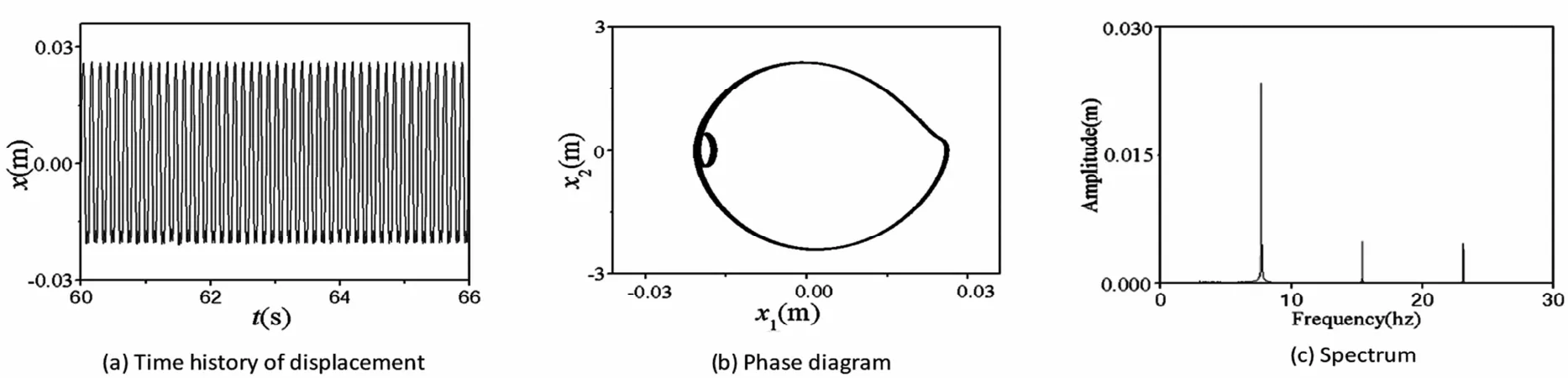
图3 激励电压2.7V时的倍周期运动Fig.3 The double periodic motion under a excitation voltage of 2.7V
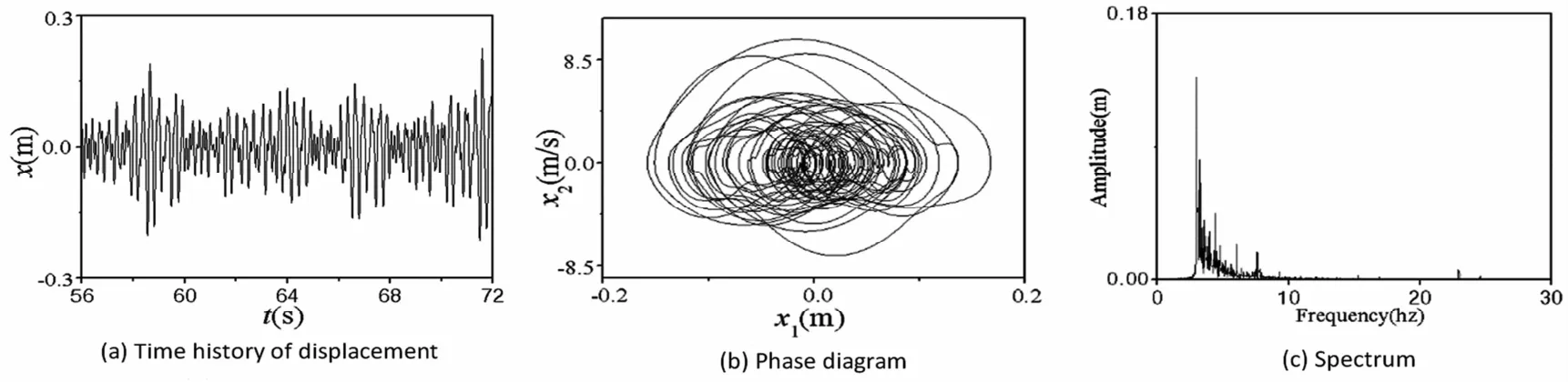
图4 激励电压4.3V时的混沌运动Fig.4 The chaotic motion under a excitation voltage of 4.3V
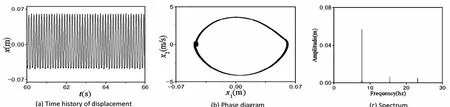
图5 激励电压6.1V时的倍周期运动Fig.5 The double periodic motion under a excitation voltage of 6.1V
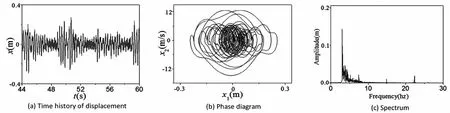
图6 激励电压9.2V时的混沌运动Fig.6 The chaotic motion under a excitation voltage of 9.2V
(2) 情况B时非线性动力响应
图7到图11给出激励频率为15.4Hz时,脱层区域中心离固支端l1/l=0.381时屈曲梁在基本参数共振下的非线性响应,实验发现随着激励电压的逐步增大,脱层屈曲梁在这一过程中相继出现周期运动,倍周期运动,混沌,倍周运动,混沌运动等.图7是激励电压为0.25V时,脱层梁出现周期运动.当继续增大激励电压时,脱层梁的振动进一步加剧,脱层两部位会周期性的相互靠近和分离,且脱层两部分互相靠近时伴随着相互碰撞而产生的撞击声.当激励电压增加到2.2V时脱层梁将会出现如图8所示的双倍周期运动.此后进一步增大激励电压,梁的振动变得更为剧烈,当电压增加到一定程度时,脱层部位会弯曲成正弦曲线状,脱层两部分之间紧贴在一起振动,并伴随杂乱无章的噪音,同时出现连续频谱,此时脱层梁的响应为如图9所示的混沌运动.当激励电压时继续增大时,脱层梁将会再次经历如图10和11所示的倍周期和混沌运动.

图7 激励电压0.25V时的周期运动Fig.7 The periodic motion under a excitation voltage of 0.25V
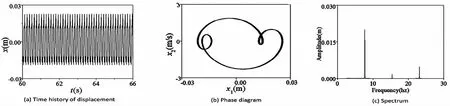
图8 激励电压2.2V时的倍周期运动Fig.8 The double periodic motion under a excitation voltage of 2.2V
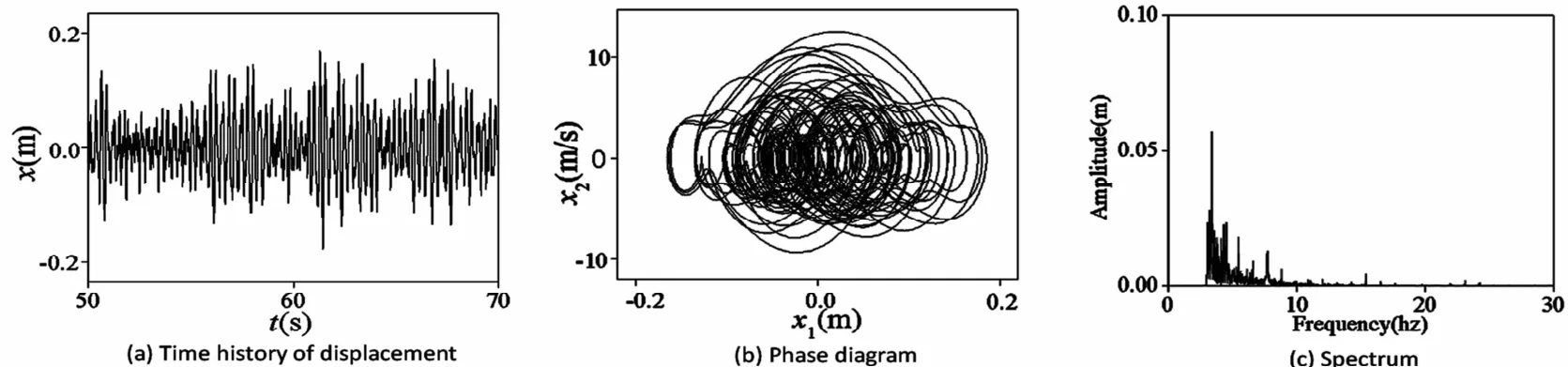
图9 激励电压3.5V时的混沌运动Fig.9 The chaotic motion under a excitation voltage of 3.5V
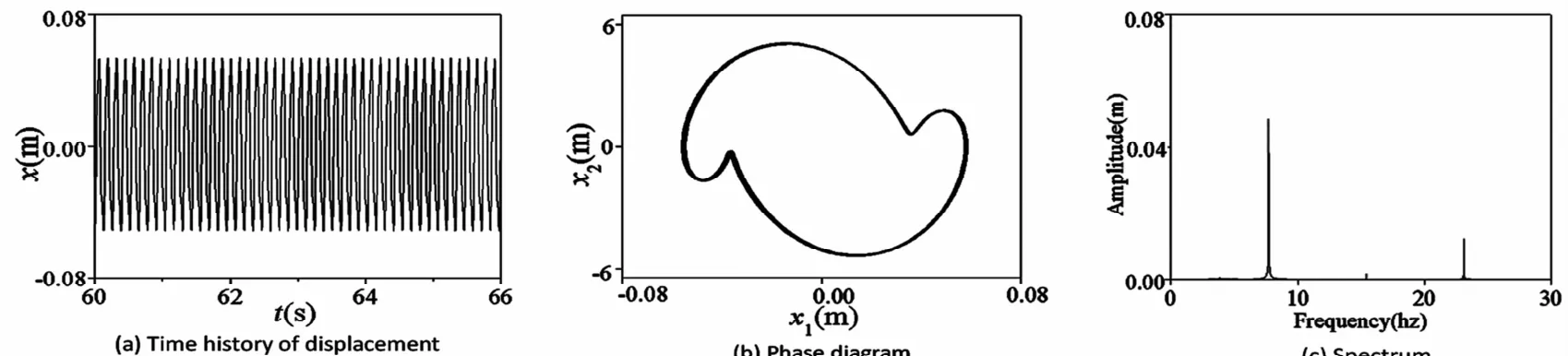
图10 激励电压5.1V时的倍周期运动Fig.10 The double periodic motion under a excitation voltage of 5.1V
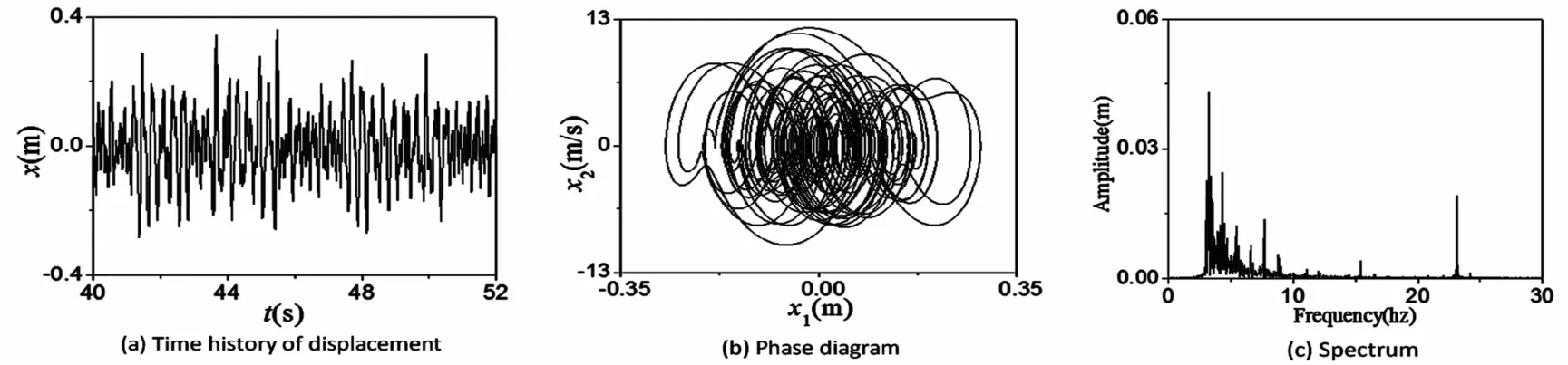
图11 激励电压7.5V时的混沌运动Fig.11 The chaotic motion under a excitation voltage of 7.5V
(3) 情况C时非线性动力响应
图12到图17给出了激励频率为14.4Hz时,脱层区域中心在梁中心位置l1/l=0.5时屈曲梁在基本参数共振下的非线性响应.如上述试验过程一样,试验中保持激励频率固定而只考虑激励电压由零逐渐增大.试验表明在较低的激励电压(荷载)下,脱层梁将会首先出现周期运动,图12给出了激励电压为0.12V时的周期运动.逐步增大激励电压后,脱层梁的振动越来越剧烈,脱层部分的相互碰撞明显加剧,当激励电压达到1.3V时,脱层梁将会出现如图13所示的倍周期运动.进一步增大激励电压至2.1V时,脱层屈曲梁将会出现如图14所示的混沌运动,此时脱层梁的脱层两部位将紧贴在一起振动,呈正弦曲线状,并伴随杂乱刺耳的噪音,系统的频谱图出现连续频谱.当继续增大激励电压,脱层屈曲梁将会进一步出现如图15,16和17所示的倍周期运动,混沌运动,四周期运动.
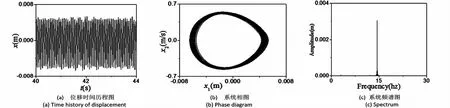
图12 激励电压0.12V时的周期运动Fig.12 The periodic motion under a excitation voltage of 0.12V

图13 激励电压1.3V时的倍周期运动Fig.13 The double periodic motion under a excitation voltage of 1.3V
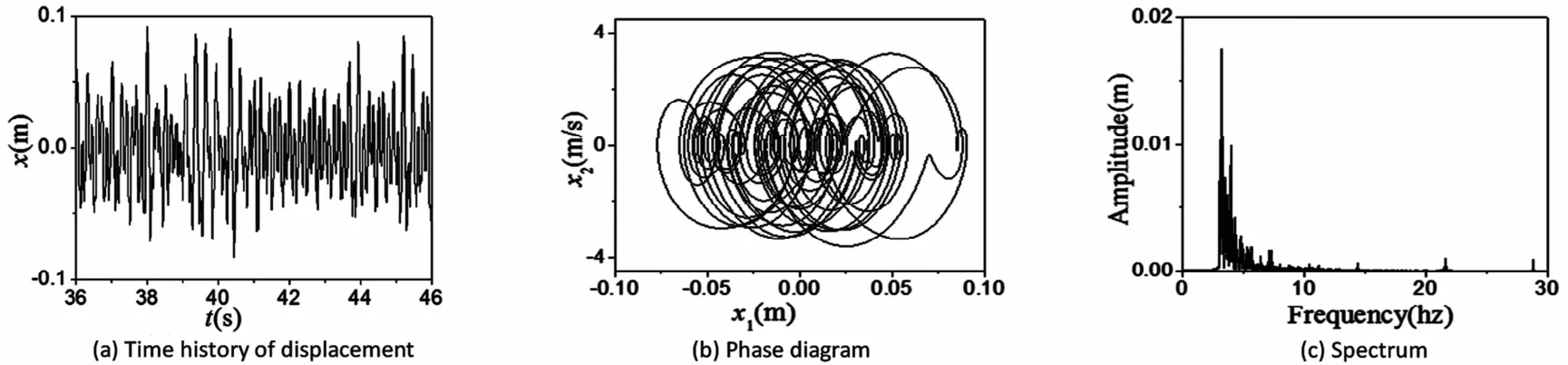
图14 激励电压2.1V时的混沌运动Fig.14 The chaotic motion under a excitation voltage of 2.1V

图15 激励电压3.2V时的倍周期运动Fig.15 The double periodic motion under a excitation voltage of 3.2V

图16 激励电压4.4V时的混沌运动Fig.16 The chaotic motion under a excitation voltage of 4.4V
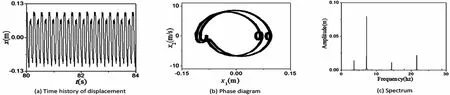
图17 激励电压5.8V时的四周期运动Fig.17 The four periodic motion under a excitation voltage of 5.8V
2.3 脱层位置对倍周期和混沌运动的影响
从上述试验可知,脱层位置对脱层梁的非线性动力学行为有重要影响.表2给出了不同脱层位置下脱层梁第一次出现双周期运动和混沌运动时的激励电压阀值.

表2 脱层位置对脱层梁系统首次出现倍周期和混沌运动时激励电压阀值的影响Table 2 The effect of delamination locations on the perioddoubling bifurcation and chaotic of the buckled beams
从表中可以看出,在相同的脱层长度下,脱层区域中心越靠近梁的中心位置,脱层梁第一次产双周期运动和混动运动时所需的激励电压越低,这表明当脱层位于梁的中心位置时,脱层梁更容易在更低的激励下产生分叉和混沌等行为.
3 结论
首次对轴向激励荷载作用下的脱层屈曲梁的非线性动力行为进行了实验研究.实验表明脱层屈曲梁在轴向周期荷载激励下存在丰富的非线性动力学行为并出现了一些特有的振动特征,同时实验还表明脱层位置对脱层屈曲梁的非线性动力行为也有明显影响.
1)脱层的存在将会降低脱层梁的自然振动频率.在相同的脱层长度下,脱层区域中心越靠近梁的中心,脱层梁的一阶振动频率越低.
2)如完整无脱层屈曲梁结构一样,在轴向周期荷载激励作用下,脱层梁结构也存在如周期分叉以及混沌运动等丰富的非线性动力学行为.且脱层位置对脱层梁的非线性动力行为有明显影响,当脱层区域中心越靠近梁的中心时,脱层梁将会在更低的激励电压下产生周期分叉以及混沌等非线性动力学行为.
3)脱层梁的非线性动力学行为具有独有的振动特征,当脱层梁产生周期,倍周期以及多周期运动时,脱层梁脱层区的两部分将会对称振动,时而分开,时而碰撞;而当脱层屈曲梁产生混沌运动时,脱层区的两部分将会紧贴在一起振动,脱层区域为正弦模态.
1 Burgreen D.Free vibration of a pin-ended column with constant distance between pin ends.Journal of Applied Mechanics,1951,18(2):135~139
2 Abou-Rayan A M,Nayfeh A H,Mook D T.Nonlinear response of a parametrically excited buckled beam.Nonlinear Dynamics,1993,4(5):499~525
3 Emam S A,Nayfeh A H.On the nonlinear dynamics of a buckled beam subjected to a primary-resonance excitation.Nonlinear Dynamics,2004,35(1):1~17
4 Emam S A,Nayfeh A H.Nonlinear responses of buckled beams to subharmonic-resonance excitations.NonlinearDynamics,2004,35(2):105~122
5 陈得良,付钦,钱长照.带集中质量复合材料层合屈曲梁参激振动的研究.动力学与控制学报,2015,13(2):101~105(Chen D L,Fu Q,Qian C Z.Research on the parametrically excited vibrations of a composite laminated buckled beam with a lumped mass.Journal of Dynamics and Control,2015,13(2):101~105(in Chinese))
6 Pirbodaghi T,Ahmadian M T,Fesanghary M.On the homotopy analysis method for non-linear vibration of beams.Mechanics Research Communications,2009,36(2):143~148
7 Nayfeh A H,Walter Lacarbonara,Char-Ming Chin.Nonlinear normal modes of buckled beams:three-to-One and one-to-Oneinternalresonances.NonlinearDynamics,1999,18(3):253~273
8 Emam S A,Nayfeh A H.Non-linear response of buckled beams to 1:1 and 3:1 internal resonances.International Journal of Nonlinear Mechanics,2013,52(6):12~25
9 Kreider W,Nayfeh,A H.Experimental investigation of single-mode responses in a fixed-fixed buckled beam.Nonlinear Dynamics,1998,15(2):155~177
10 Nagai K,Maruyama S,Sakaimoto K,Yamaguchia T.Experiments on chaotic vibrations of a post-buckled beam withan axial elastic constraint.Journal of Sound and Vibration,2007,304(3-5):541~555
11 Mahmoodi S N,Jalili N,Khadem S E.An experimental investigation of nonlinear vibration and frequency response analysis of cantilever viscoelastic beams.Journal of Sound and Vibration,2008,311(3-5):1409~1419
12 Saravanis D A,Hopkins D A.Effects of delaminations on the dynamic characteristics of composite laminates analysis and experiments.Journal of Sound and Vibration,1996,195(5):977~993
13 Whitcomb J D.Finite element analysis of instability related delamination growth.Journal of Composite Materials,1981,15(9):403~428
14 Chai H,Babcock C A,Knauss W G.One dimensional modeling of failure in laminated plates by delaminationbuckling.International Journal of Solids and Structurees,1981,17(11):1069~1083
15 Luo H,Hanagud S.Dynamics of delaminated beams.International Journal of Solids and Structures,2000,37(10):1501~1519
16 Wang J,Tong L.A study of the vibration of delaminated beams using a nonlinear anti-interpenetration constraintmodel.Composite Structures,2002,57(1-4):483~488
17 Arkadiusz J..Zak.Non-linear vibration of a delaminated composite beam.Key Engineering Materials,2005,293-294:607~616
Received 2 May 2015,revised 18 July 2015.
*The project supported by the National Natural Science Foundation of China(11172051,11272270)and the National Natural Science Foundation of Hunan province(2015JJ4006)
†Corresponding author E-mail:deliang_chen@126.com
EXPERIMENTAL STUDY ON THE VIBRATION OF DELAMINATED BUCKLED BEAMS WITH DIFFERENT DELAMINATION LOCATIONS*
Chen Deliang1†Fu Qin2Chen Changping3
(1.School of Civil Engineering and Architecture,Changsha University of Science&Technology,Changsha 410014,China)(2.Shenzhen Road&Bridge Construction Group Co.Ltd,Shenzhen 518024,China)(3.Department of Civil Engineering and Architecture,Xiamen University of Technology,Xiamen 361024,China)
The nonlinear response of delaminated buckling beams with different delamination locations under axial periodic excitation was examined through experimental investigation.The time history of displacement,phase diagrams and spectrum are described and discussed.The research demonstrates the delaminated buckled beam performs nonlinear dynamic motions,such as period,period-doubling as well as chaos.The experimental results show that in the case of the same delamination length,the delaminated location greatly affect the dynamic characteristics of delaminated buckled beam.And when the central of the delamination region is closer the mid-span of beam,the first order frequency of delaminated beam is lower.Moreover,the delaminated buckled beam more easily experiences the periodic motion,doubling periodic motion and chaotic motion at lower excited frequency and loads.
delamination buckled beam,experiment,parametric vibration,delamination locations,nonlinear dynamic response
10.6052/1672-6553-2015-056
2015-05-02收到第1稿,2015-07-18收到修改稿.
*国家自然科学基金资助项目(11172051,11272270)及湖南省自然科学基金资助项目(2015JJ4006)
†通讯作者E-mail:deliang_chen@126.com

