分数阶Birkhoff系统基于Caputo导数的Noether对称性与守恒量*

周燕张毅

（1.苏州科技学院数理学院，苏州 215009）（2.苏州科技学院土木工程学院，苏州 215011）（3.苏州市工业园区娄葑学校，苏州 215021）

分数阶Birkhoff系统基于Caputo导数的Noether对称性与守恒量*

周燕1，3张毅2†

（1.苏州科技学院数理学院，苏州 215009）（2.苏州科技学院土木工程学院，苏州 215011）（3.苏州市工业园区娄葑学校，苏州 215021）

在Caputo分数阶导数下研究分数阶Birkhoff系统的Noether对称性与守恒量.首先，定义Caputo分数阶导数下的分数阶Pfaff作用量，建立分数阶Birkhoff方程及其相应的横截性条件；其次，基于Pfaff作用量在无限小变换下的不变性，分别在时间不变和时间变化的无限小变换下，给出了不变性条件.基于Frederico和Torres的分数阶守恒量概念，建立了分数阶Birkhoff系统的Noether定理，揭示了分数阶Noether对称性与分数阶守恒量之间的内在联系.

分数阶Birkhoff系统，分数阶Noether对称性，分数阶守恒量，分数阶Pfaff作用量，Caputo分数阶导数

引言

动力学系统对称性的研究一直是分析力学的一个重要发展方向.1918年Noether［1］研究了Hamilton作用量在无限小变换下的不变性质，揭示了力学系统的守恒量与其内在的动力学对称性之间的关系.Djuki c′和Vujanovi c′［2］将Noether定理推广到完整非保守系统，李子平［3］，Bahar［4］，刘端［5］进一步将Noether定理推广到非完整非保守系统.梅凤翔［6］通过引进r参数变换群的无限小群变换的广义准对称性概念，建立了Birkhoff系统的Noether理论.近年来，对Noether对称性的研究已经取得了一系列重要成果［7-10］.

分数阶微积分的概念最早出现在L’Hospital于1695年写给Leibniz的信中，但是直到1974年第一本关于分数阶微积分理论的著作才问世［11］.近20年来，随着分数阶微积分应用领域的不断拓展，分数阶微积分及其应用研究有了很大的发展.1996年，Riewe［12-13］首次将分数阶微积分应用于非保守系统动力学建模，提出并初步研究了分数阶变分问题.之后，Agrawal［14-15］，Baleanu［16-17］，Atanackovi c′［18-19］，El-Nabulsi［20-22］等对分数阶变分问题进行了深入研究.Frederico和Torres最早开展了分数阶Noether对称性与守恒量的研究［23-25］，基于Riemann-Liouville分数阶导数定义［23］，Caputo分数阶导数定义［24］，Riesz-Caputo分数阶导数定义［25］，分别考虑时间不变和时间变化的无限小变换作用，得到了分数阶Noether定理.在此基础上，Frederico和Torres进一步给出了Hamilton系统的分数阶Noether定理［26］.此外，Frederico和Torres基于El-Nabulsi动力学模型研究了类分数阶作用变分的不变性问题［27-28］.近年来，约束力学系统基于分数阶模型的Noether对称性与守恒量的研究已经取得了一些重要成果［29-34］.但是，研究主要限于分数阶Lagrange系统和分数阶Hamilton系统.

本文基于Caputo分数阶导数的定义，研究分数阶Birkhoff系统的分数阶Noether对称性.从Pfaff作用量在无限小变换下的不变性出发，分别在时间不变和时间变化的无限小变换下，研究了分数阶Pfaff作用量的不变性，建立了分数阶Birkhoff系统的Noether定理.

1 分数阶导数

本节列出研究所涉及的Riemann-Liouville分数阶导数和Caputo分数阶导数的定义及相关性质，详细的证明和讨论可参见［35-36］.

其中Γ（*）是Euler-Gamma函数，α是导数的阶，且m-1≤α＜m，m为正整数.如果α是整数，上述分数阶导数成为整数阶导数，有

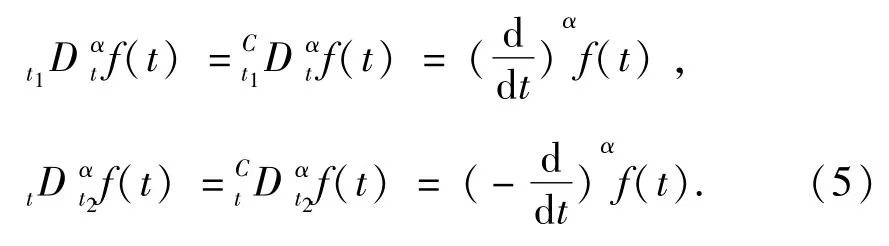
设f和g是区间[t1，t2]上的光滑函数，则Caputo导数下的分数阶分部积分公式为

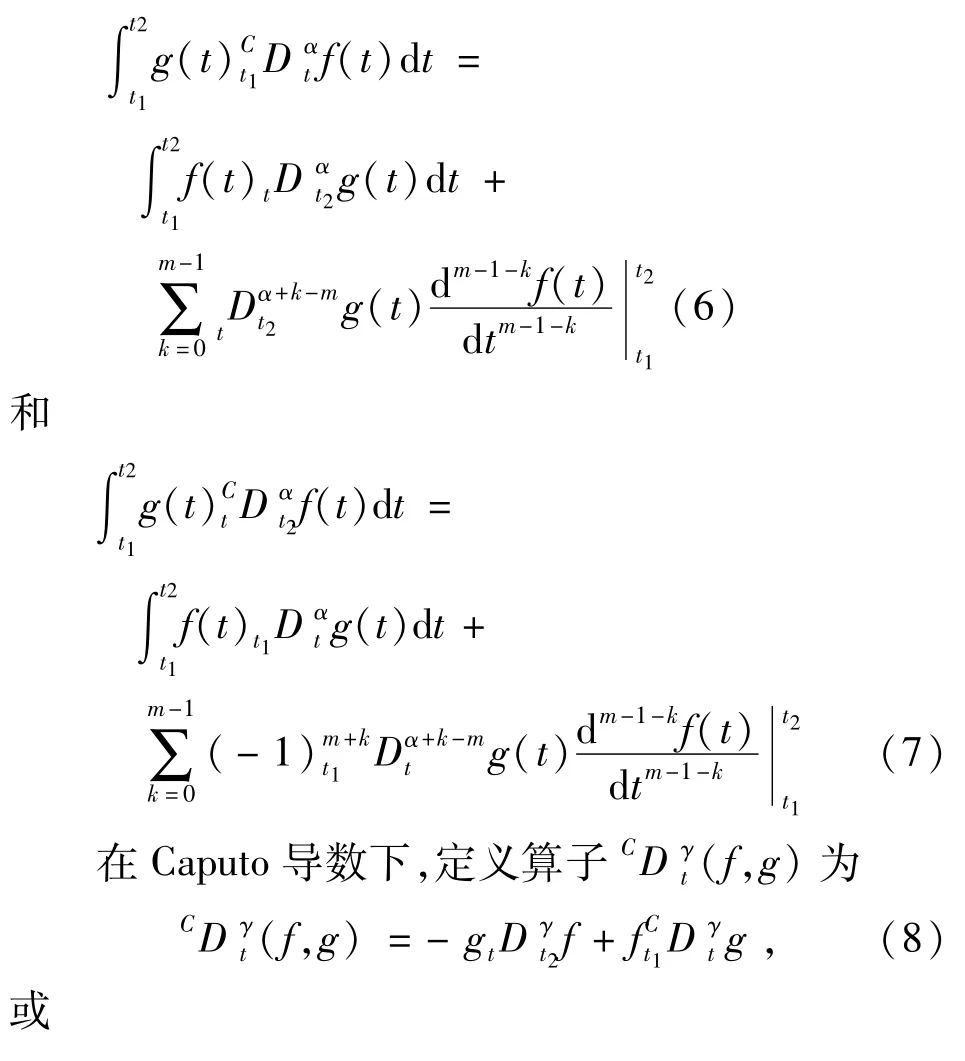
2 分数阶Birkhofff方程

考虑由2n个Birkhoff变量aμ（μ＝1，2，…，2n）来描述的Birkhoff系统.假设系统的Birkhoff函数B＝B（t，aν），Birkhoff函数组为Rμ＝Rμ（t，aν），分数阶导数的阶为α，且0＜α＜1.积分泛函

称为基于Caputo导数的分数阶Pfaff作用量.等时变分原理

带有交换关系

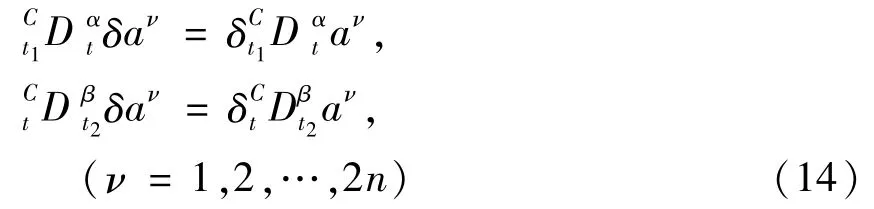
以及端点条件

称为基于Caputo导数的分数阶Pfaff-Birkhoff原理.

由分数阶Pfaff-Birkhoff原理（13）-（15）容易导出如下方程［37］

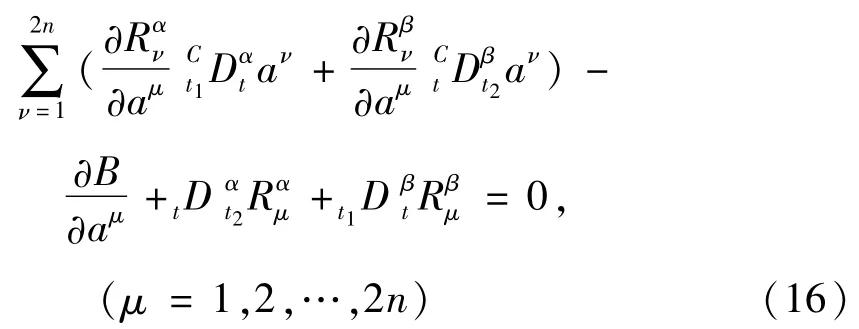
以及相应的横截性条件

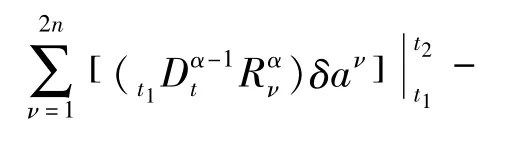
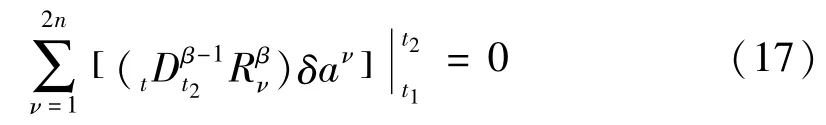
由端点条件（15）可得横截性条件（17）恒成立.方程（16）称为基于Caputo分数阶导数的分数阶Birkhoff方程.

由分数阶Birkhoff方程（16）可以得到经典Birkhoff方程.实际上，令分数阶Pfaff作用量（12）中不含Caputo右导数，即

则分数阶Birkhoff方程（16）成为

当α→1时，方程（19）为

方程（20）为经典的Birkhoff方程.因此，经典的整数阶Birkhoff方程是分数阶Birkhoff方程（16）的特例.

3 分数阶Birkhoff系统的Noether定理

首先，引入Frederico和Torres提出的分数阶守恒量概念［23］.

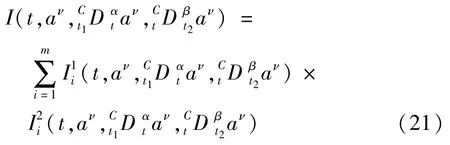
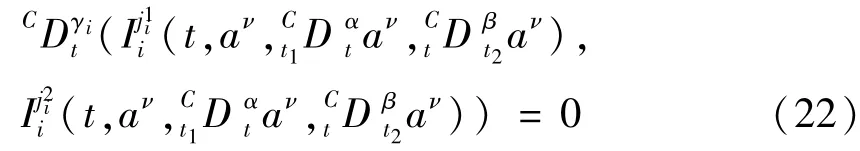
其次，引进时间不变的单参数无限小变换群

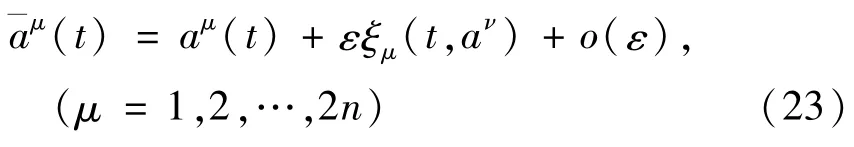
我们来定义分数阶Birkhoff系统在无限小变换（23）下的Noether对称性，并给出相应的分数阶守恒量.

定义2 如果分数阶Pfaff作用量（12）在无限小变换（23）作用下，对于任意的子区间[T1，T2]⊆（t1，t2），成立

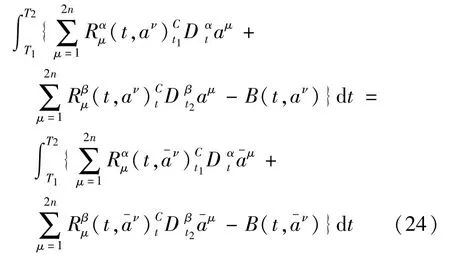
则称这种不变性为分数阶Birkhoff系统在时间不变的无限小变换下的Noether对称性.

定理1 如果分数阶Pfaff作用量（12）在变换（23）作用下保持不变，那么

成立.

证明 由积分区间[T1，T2]的任意性，由（24）式可得

式（26）两边对ε求导，然后令ε＝0，有

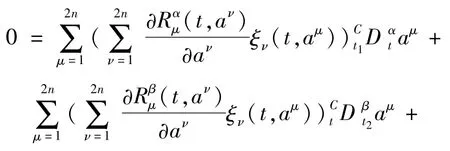
此时（27）式即为（25）式，证毕.

定理2 如果分数阶Pfaff作用量（12）在定义2下保持不变，那么

是分数阶Birkhoff系统（16）的分数阶守恒量.

证明 由分数阶Birkhoff方程（16）可得

由于分数阶Pfaff作用量（12）在定义2下保持不变，故将（29）式代入（25）式，得

从而，由分数阶守恒量的定义1可知（28）式是该情形下的分数阶守恒量.

最后，引进时间变化的单参数无限小变换群

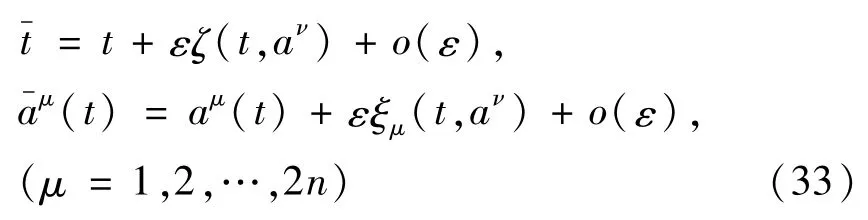
我们来定义分数阶Birkhoff系统在无限小变换（33）下的Noether对称性，并给出相应的分数阶守恒量.

定义3 如果分数阶Pfaff作用量（12）在无限小变换（33）作用下，对于任意的子区间[T1，T2]⊆（t1，t2），成立

则称这种不变性为分数阶Birkhoff系统在时间变化的无限小变换下的Noether对称性.

定理3 如果分数阶Pfaff作用量（12）在定义3下保持不变，那么

是分数阶Birkhoff系统（16）的分数阶守恒量.证明 取关于时间t（t是独立变量）的李普希兹变换

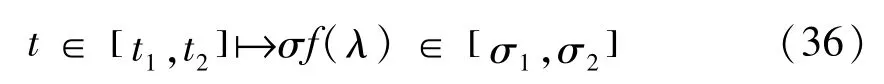
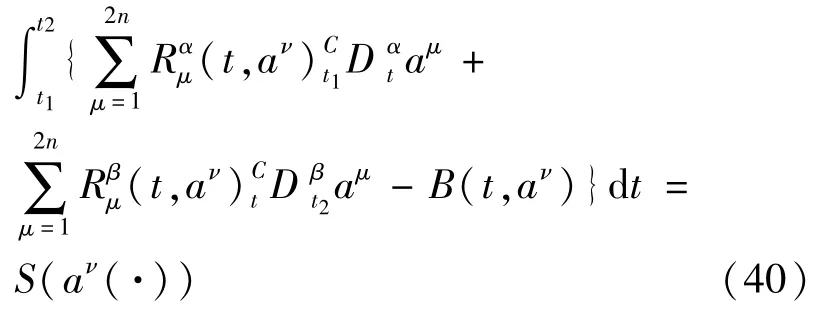
如果分数阶Pfaff作用量（12）在定义3下保持不变，那么分数阶Pfaff作用量（37）在定义2下保持不变，由定理2，我们得到

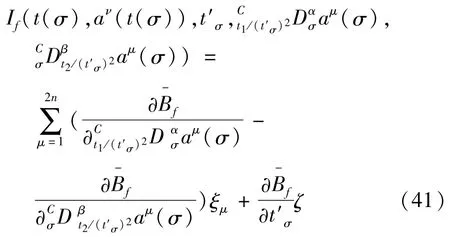
式（41）是系统的分数阶守恒量.当λ＝0时，有

将式（43）和（44）代入式（41），我们得到守恒量（35）.证毕.

定理2和定理3称为分数阶Birkhoff系统在Caputo导数下的分数阶Noether定理，它们揭示了分数阶Noether对称性与分数阶守恒量之间的关系.利用分数阶Noether定理，可由分数阶Birkhoff系统的Noether对称性找到相应的分数阶守恒量.

4 算例

下面举例说明结果的应用.

例考虑二阶Birkhoff系统，其分数阶Pfaff作用量为

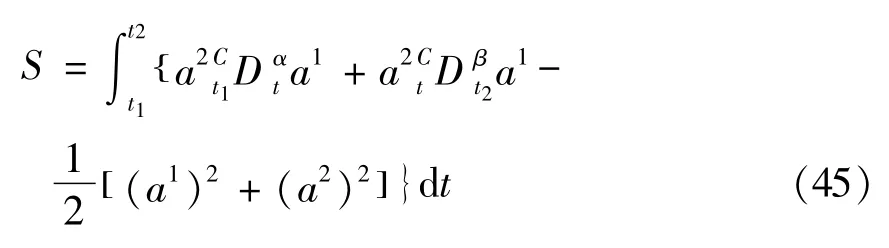
试研究该Birkhoff系统的分数阶Noether对称性与分数阶守恒量.

由作用量（45）可知，系统的Birkhoff函数和Birkhoff函数组分别为

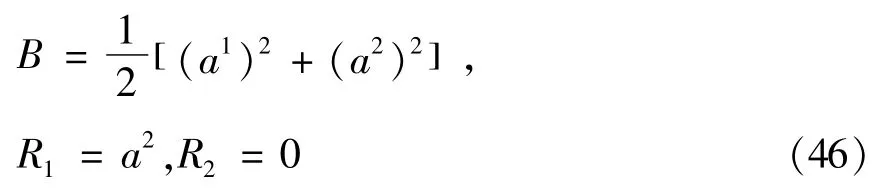
显然，存在如下Noether对称变换

使得分数阶Pfaff作用量（45）在定义3意义下不变，故由定理3该系统的分数阶守恒量为

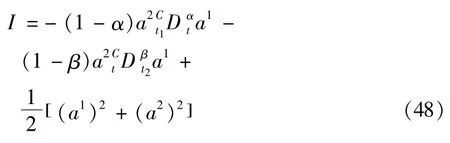
如果作用量（45）中只含左导数，令α→1，则守恒量（48）给出

式（49）是整数阶模型下Birkhoff系统（46）的守恒量.

5 结论

近20年来，分数阶微积分被成功地广泛应用于科学和工程的各个领域.分数阶微积分也被用于非保守系统或耗散系统的动力学建模，从而可以解决用经典的整数阶导数下的方法难以解决的问题.本文的主要工作：一是基于Caputo分数阶导数提出分数阶Pfaff变分问题，建立了分数阶力学系统的分数阶Birkhoff方程（16）；二是基于分数阶Pfaff作用量在无限小变换下的不变性，定义了分数阶Birkhoff系统的Noether对称性，依据Frederico和Torres提出的分数阶守恒量概念，给出了分数阶Birkhoff系统的守恒量，建立了分数阶Noether定理，从而揭示了分数阶对称性与分数阶守恒量的内在联系.经典的Birkhoff系统是本文之特例，因此本文结果具有普遍意义.

1 Noether E.Invariant variation problems.Transport Theory and Statistical Physics，1971，1（3）：186～207

3 李子平.约束系统的变换性质.物理学报，1981，30（12）：1659～1671（Li Z P.The transformation properties of constrained system.Acta Physica Sinica，1981，22（2）：125～138（in Chinese））

4 Bahar L Y，Kwatny H G.Extension of Noether’s theorem to constrained nonconservative dynamical systems.International Journal of Non-Linear Mechanics，1987，22（2）：125～138

5 Liu D.Noether’s theorem and its inverse of nonholonomic nonconservative dynamical systems.Science in China（Series A），1991，34（4）：419～429

6 Mei F X.The Noether’s theory of Birkhoffian systems.Science in China（Serie A），1993，36（12）：1456～1467

7 梅凤翔.李群和李代数对约束力学系统的应用.北京：科学出版社，1999（Mei F X.Applications of Lie groups and Lie algebras to constrained mechanical systems.Beijing：Science Press，1999（in Chinese））

8 Luo S K，Cai J L，Jia L Q.Noether symmetry can lead to non-noether conserved quantity of holonomic nonconservative systems in general Lie transformations.Communications in Theoretical Physics（Beijing，China），2005，43（2）：193～196

9 FuJ L，Chen B Y，Chen L Q.Noether symmetries of discrete nonholonomic dynamical systems.Physics Letters A，2009，373（4）：409～412

10 梅凤翔，吴惠彬.分析动力学三个问题的研究进展.动力学与控制学报，2014，12（1）：1～8（Mei F X，Wu H B.Advances in three problems of analytical dynam-ics.Journal of Dynamics and Control，2014，12（1）：1～8（in Chinese））

11 Oldham K B，Spanier J.The fractional calculus.San Diego：Academic Press，1974

12 Riewe F.Nonconservative Lagrangian and Hamiltonian mechanics.Physical Review E，1996，53（2）：1890～1899

13 Riewe F.Mechanics with fractional derivatives.Physical Review E，1997，55（3）：3581～3592

14 Agrawal O P.Formulation of Euler-Lagrange equations for fractional variational problems.Journal of Mathematical Analysis and Applications，2002，272（1）：368～379

15 Agrawal O P.Generalized Euler-Lagrange equations and transversality conditions for FVPs in terms of the Caputo derivative.Journal of Vibration and Control，2007，13（9～10）：1217～1237

16 Baleanu D，Avkar T.Lagrangians with linear velocities within Riemann-Liouville fractional derivatives.Nuovo Cimento B，2003，119（1）：73～79

17 Baleanu D，Trujillo J I.A new method of finding the fractional Euler-Lagrange and Hamilton equations within Caputo fractional derivatives.Communications in Nonlinear Science and Numerical Simulation，2010，15（5）：1111～1115

20 El-Nabulsi A R.A fractional approach to nonconservative Lagrangian dynamical systems.Fizika A，2005，14（4）：289～298

21 El-Nabulsi A R，Torres D F M.Fractional action-like variational problems.JournalofMathematicalPhysics，2008，49（5）：053521

22 El-Nabulsi A R.Fractional variational problems from extended exponentially fractional integral.Applied Mathematics and Computation，2011，217（22）：9492～9496

23 Frederico G S F，Torres D F M.A formulation of Noether’s theorem for fractional problems of the calculus of variations.Journal of Mathematical Analysis and Applications，2007，334（2）：834～846

24 Frederico G S F.Fractional optimal control in the sense of Caputo and the fractional Noether’s theorem.International Mathematical Forum，2008，3（10）：479～493

25 Frederico G S F，Torres D F M.Fractional Noether’s theorem in the Riesz-Caputo sense.Applied Mathematics and Computation，2010，217（3）：1023～1033

26 Frederico G S F，Torres D F M.Fractional conservation laws in optimal control theory.Nonlinear Dynamics，2008，53（3）：215～222

27 Frederico G S F，Torres D F M.Constants of motion for fractional action-like variational problems.International Journal of Applied Mathematics，2006，19（1）：97～104

28 Frederico G S F，Torres D F M.Non-conservative Noether’s theorem for fractional action-like problems with intrinsic and observer times.International Journal of Ecological Economics＆Statistics，2007，9（F07）：74～82

30 Malinowska A B，Torres D F M.Introduction to the fractional calculus of variations.London：Imperial College Press，2012

31 Zhang S H，Chen B Y，Fu J L.Hamilton formalism and Noether symmetry for mechanico electrical systems with fractional derivatives.Chinese Physics B，2012，21（10）：100202

32 Zhang Y，Zhou Y.Symmetries and conserved quantities for fractional action-like Pfaffian variational problems.Nonlinear Dynamics，2013，73（1～2）：783～793

33 Long Z X，Zhang Y.Noether’s theorem for fractional variational problem from El-Nabulsi extended exponentially fractional integral in phase space.Acta Mechanica，2014，225（1）：77～90

34 Long Z X，Zhang Y.Fractional Noether theorem based on extended exponentially fractional integral.International Journal of Theoretical Physics，2014，53（3）：841～855

35 Podlubny I.Fractional differential equations.San Diego：Academic Press，1999

36 Kilbas A A，Srivastava H M，Trujillo J J.Theory and applications of fractional differential equations.Amsterdam：Elsevier B V，2006

37 Zhou Y，Zhang Y.Fractional Pfaff-Birkhoff principle and Birkhoff’s equations within Caputo fractional derivatives.Journal of Jiangxi Normal University（Natural Science），2014，38（2）：153～157

Received 23 September 2014，revised 20 December 2014

*The project supported by the National Natural Science Foundation of China（10972151，11272227）and the Innovation Program for Postgraduate in Higher Education Institutions of Jiangsu Province（CXZZ11_0949）

†Corresponding author E-mail：zhy@mail.usts.edu.cn

NOETHER SYMMETRY AND CONSERVED QUANTITY FOR FRACTIONAL BIRKHOFFIAN SYSTEMS IN TERMS OF CAPUTO DERIVATIVES*

Zhou Yan1，3Zhang Yi2†
（1.College of Mathematics and Physics，Suzhou University of Science and Technology，Jiangsu Suzhou 215009，China）（2.College of Civil Engineering，Suzhou University of Science and Technology，Jiangsu Suzhou 215011，China）（3.Suzhou Industrial Park Loufeng School，Jiangsu Suzhou 215021，China）

This paper studies the Noether symmetry and corresponding conserved quantity for fractional Birkhoffian systems in terms of Caputo fractional derivatives.Firstly，the fractional Pfaff action is defined within Caputo fractional derivatives.The fractional Birkhoff’s equations and corresponding transversality conditions are also established.Secondly，based on the invariance of the Pfaff action under the infinitesimal transformations，the conditions of invariance are given under a special one-parameter group of infinitesimal transformations without transforming the time as well as a general one-parameter group with transforming the time，respectively.Finally，according to the notion of fractional conserved quantity presented by Frederico and Torres，the Noether theorem for the fractional Birkhoffian systems is constructed，which states the relationship between a fractional Noether symmetry and a fractional conserved quantity.

fractional Birkhoffian system，fractional Noether symmetry，fractional conserved quantity，fractional Pfaff action，Caputo fractional derivative

10.6052/1672-6553-2015-017

2014-09-23收到第1稿，2014-12-20收到修改稿.

*国家自然科学基金资助项目（10972151，11272227）和江苏省普通高校研究生科研创新计划资助项目（CXZZ11_0949）

†通讯作者E-mail：zhy@mail.usts.edu.cn