旋转圆环平面外振动的行波法研究*
何虹 黄迪山
(上海大学机电工程与自动化学院,上海 200072)
旋转圆环平面外振动的行波法研究*
何虹 黄迪山†
(上海大学机电工程与自动化学院,上海 200072)
以高速球轴承保持架为应用对象,针对旋转薄壁圆环的平面外振动问题,开展弹性波传播的基本特性研究,分析平面外波动的色散方程、波数、截止频率、相速度以及位移耦合系数.基于行波动力学方法,根据波动正向传递的判据,将正负行波的波数进行分离.结合相位封闭原理和波传递矩阵,建立旋转圆环的频率特征方程.文中算例给出了旋转薄壁圆环平面外振动的固有频率,对其计算结果与文献结果作了比较,验证了计算方法的准确性.
平面外振动,旋转圆环,行波法,波数
引言
行波法是将弹性结构的振动描述成波导中波的传播和衰减.近几年,研究行波法对平面内静止结构的工作已取得一定进展.Mead D J[1]提出相位封闭原理(the phase-closed principle),奠定了弹性结构行波动力学分析的基础,使行波法成为一种有效的结构计算方法,该方法逐渐应用于梁、转子等结构的振动分析之中.
最近,Mei C推导了Timoshenko梁中波的传递关系,给出了波在不连续节点处的散射特性,并且根据结构振动的广义位移连续性条件和广义力平衡条件,推导出了L型[2]、H型[3]、多层型等其它平面框架结构节点处的反射和透射矩阵,成功地计算平面框架结构的振动特性[4].Chouvion B[5]使用行波法计算环-梁结构的微机电系统传感器的动力学参数,并且利用这些参数对传感器进行优化设计.Kang B[6]研究了平面内静止弯曲梁的行波动力学建模方法,在忽略转动惯量和剪力对梁微元体的影响情况下,求得了在扩张和非扩张情况下的弯曲Euler-Bernoulli梁模型的行波解.然而,行波法应用于旋转圆环的研究仅刚刚起步.文献[7]根据Euler-Bernoulli梁理论,用行波法给出了平面内旋转不等截面圆环波谱特性以及固有频率.
另外,研究弯曲梁平面外振动问题基本上集中于静止状态.Lee S Y[8]在忽略转动惯量和剪力的情况下,研究了静止非匀质弯曲梁平面外振动特性.Chouvion B[9]使用行波法研究了平面外静止环-梁结构的自由和受迫振动问题.对于旋转类物体研究,有关振动问题的涉及较少.Eley R[10]考虑了Coriolis耦合作用的影响,用模态法分析了基于旋转圆环的多轴速度传感器结构,得到平面外振动特性.蒋宝坤等人[11]运用多尺度法研究了平面内旋转粘弹性夹层梁的非线性自由振动特性.周延泽等人[12]使用模态分析法给出了考虑转速影响的轴承保持架在平面内振动和平面外弯曲扭转耦合振动的固有频率表达式.
本文将以高速球轴承保持架为应用对象,基于Euler-Bernoulli旋转弯曲梁模型,用波动法研究平面外轴向和弯曲耦合振动,分析振动波在旋转弯曲梁中传播的基本特性.根据振动波正反向传递相位封闭的原理,获得旋转圆环平面外振动的频率特征方程以及固有频率.最后,将行波计算结果与文献[13]结果进行比较,分析其一致性.
1 运动方程
图1所示的是一个以转速Ω绕着Z轴旋转的薄壁圆环.沿圆周中性线的坐标由y表示,与中性线垂直的径向坐标和轴向坐标分别由x和z表示.横截面的宽和高分别由b和h表示.圆环横截面中性线在轴向的位移为w,绕y轴的扭转角位移为φ.
根据文献[13]得到薄壁圆环平面外的振动方程:
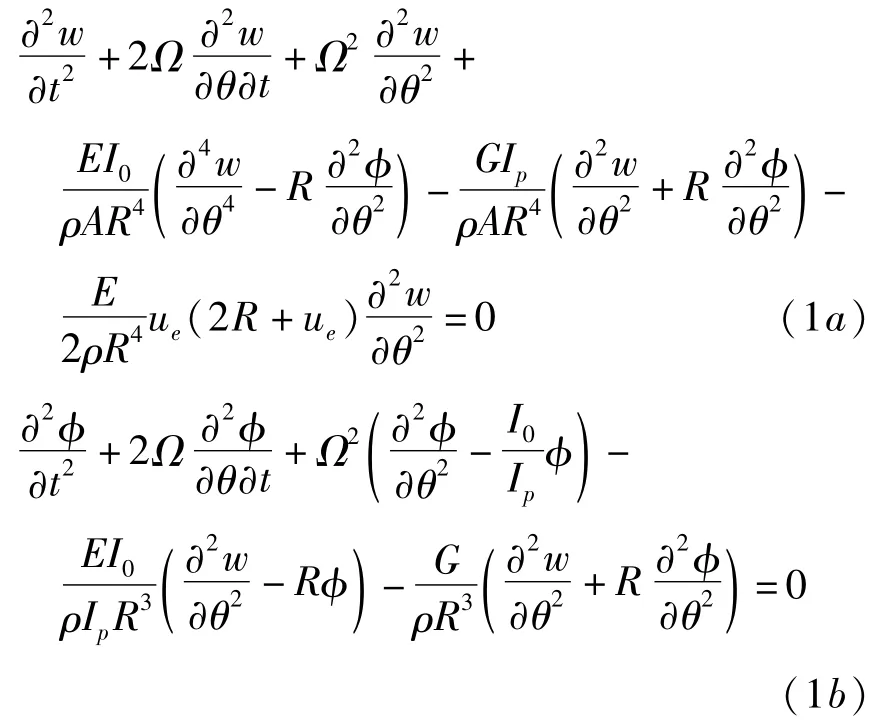
由方程(1a)和(1b)可知,轴向位移w和扭转角位移φ是互为耦合的.其中,E为弹性模量,G为剪切模量,I0为x轴的惯性矩,Ip为y轴的极惯性矩,R为曲率半径,Ω为转速,A为横截面积,t为时间,θ为角度坐标.ue为常数,表示为ue=R.如果将Ω=0代入到方程(1)中,则简化后的振动方程与文献[9]所述的振动方程一致.
基于Euler-Bernoulli梁理论的弯曲梁,振动弹性波动是多色波,存在色散现象.在研究旋转圆环波动的传递特性时,设振动方程(1)的通解为
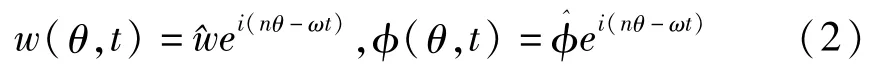
将通解(2)代入到方程(1)中,并写成如下矩阵的形式:
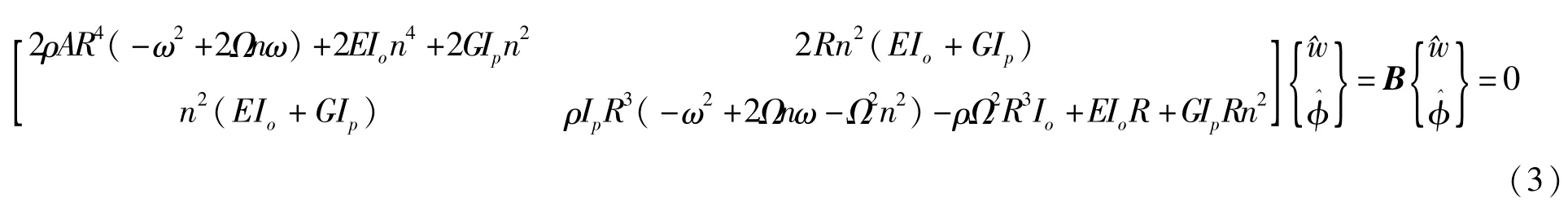
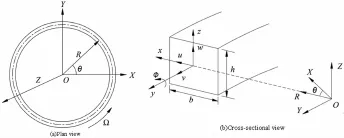
图1 自由旋转薄壁圆环模型Fig.1 Model of free rotating thin ring
令det(B)=0,得到旋转圆环平面外波动的色散方程
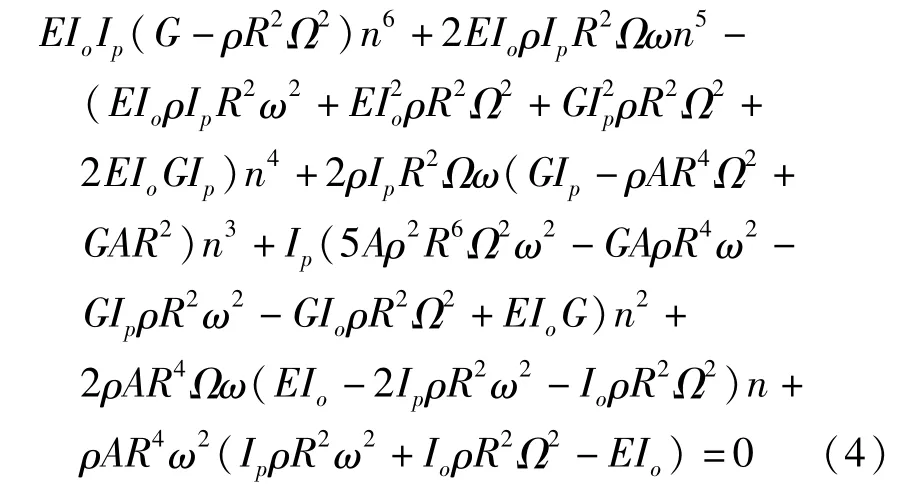
从公式(3)可得扭转角位移φ和轴向位移w的耦合系数β,其表达式如下:
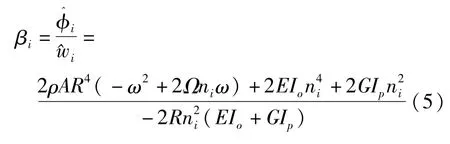
因此,轴向位移w和扭转角位移φ的波动表达为
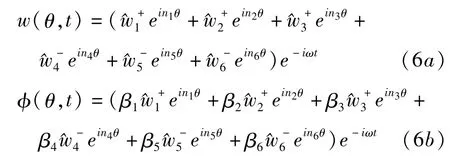
其中,上标“+”和“-”分别表示正传波和负传波的波幅系数;下标“1~3”和“4~6”分别表示正方向和负方向传播的波数.
2 波模式
根据旋转圆环平面外波动的色散方程(4),在给定频率下,应用高次代数方程数值解方法,能方便地得到某频率下对应的6个波数,不同频率对应着不同波数,从而构成波谱图.根据波谱图形特性,将波谱分为四种波模式加以讨论.
对于波模式,学者Lee[14]对于正向传递的波给出了如下定义:

(i)如果波数是复数,那么正传波波数的虚部为负数或零,并且波在正向衰减传递;(ii)如果波数是实数,那么正传波波数对应的导数为正.
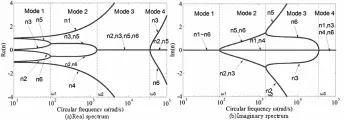
图2 Ω=0时波谱图Fig.2 Wavenumber spectrum when Ω=0
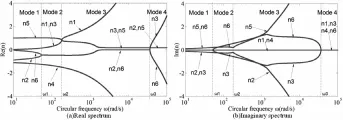
图3 Ω=100rad/s波谱图Fig.3 Wavenumber spectrum when Ω=100rad/s
图2 对应于静止圆环的四种波模式,而图3对应于旋转圆环的四种波模式.图2和图3是圆环在(101,105)频率范围内的谱曲线(几何尺寸和物理参数参见6.3算例).图中分叉点ω1、ω2、ω3,表明了静止和旋转圆环波数的四种模式.
2.1 静止圆环的四种波模式
(a)模式一:6个实波数,且n4=-n1,n5=-n2,n6=-n3.
(b)模式二:2个实波数和4个复波数,且n4=-n1,n5=,n6=.(*表示共轭)
(c)模式三:2个实波数和4个虚波数,且n4=-n1,n5=,n6=.
(d)模式四:4个实波数和2个虚波数,且n4=-n1,n5=,n6=-n3.
2.2 旋转圆环的四种波模式
(a)模式一:2个实波数和4个复波数,且|n1|<|n4|,|n2|<|n5|,|n3|<|n6|.
(b)模式二:2个实波数和4个复波数,且|n1|<|n4|,|n2|<|n5|,|n3|<|n6|.
(c)模式三:2个实波数和4个复波数,且|n1|<|n4|,|n2|<|n5|,|n3|>|n6|.
(d)模式四:4个实波数和2个复波数,且|n1|<|n4|,|n2|=|n5|,|n3|=|n6|.
薄壁圆环静止时,正行波的波数与负行波的波数相等,波谱图对称;而在圆环运动时,由于色散方程(4)中加入了转速项,波数随转速而改变,波谱实部不再保持对称.
3 相速度
波的相速度或相位速度是指波的相位在空间中传递的速度.相速度c与圆频率ω、波数n的关系如下:

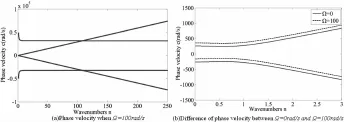
图4 相速度图Fig.4 Phase velocity
图4 (a)是Ω=100rad/s时,振动波在圆环平面外传播的相速度图.图4(b)是波在圆环平面外静止和转动时的相速度局部放大图;从图中可以看出,波在静止圆环的相速度是关于0线对称的;转速Ω改变了波相速度的对称性;波在旋转圆环上的相速度大于波在静止圆环上的相速度.
4 波在旋转圆环中的截止频率
考虑旋转圆环中的长波情况,即n→0,对色散方程(4)求极限可得到旋转圆环的截止频率,如下所示:
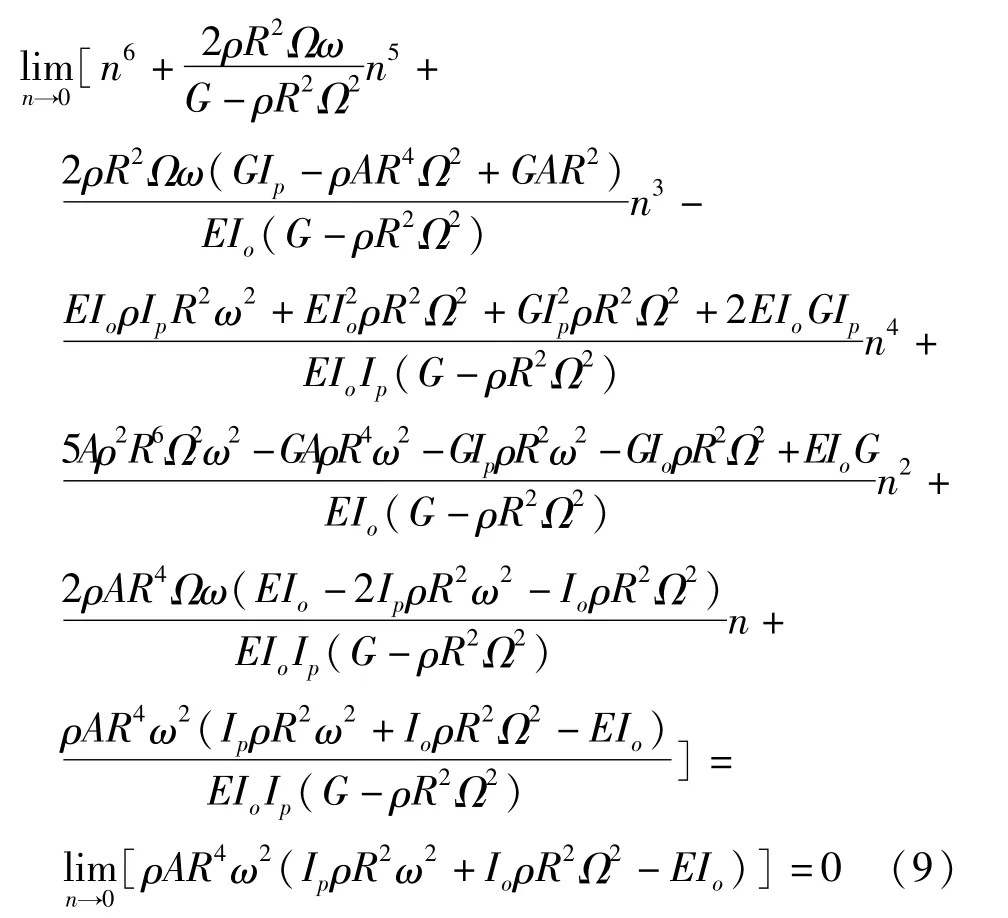
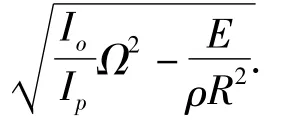
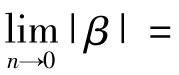
5 位移耦合系数
为了分析波幅耦合作用的影响,图5给出了位移耦合系数β随频率变化的曲线.图5(a)和图5(b)分别为圆环在平面外静止和转动时的耦合系数β1~β6曲线.β1~β6分别对应波数n1~n6.图5中曲线的分叉点将曲线分为四个区间,这四个区间与四个波模式相对应.
图5(a)是圆环在平面外静止时β的耦合曲线.从耦合系数β的表达式可知,位移耦合系数β的量级为104,在模式二和模式三之间达到最大值,说明n1~n6始终对应以扭转运动为主导的波动.图5(b)是Ω=100rad/s时,圆环在平面外运动时β的耦合曲线.由于转速的影响,耦合系数发生很大的变化,原本绝对值或模相等的正负波数对不再对称,但扭转波动仍占主导地位.
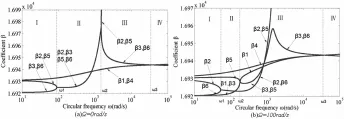
图5 位移耦合系数Fig.5 The ratio of axial displacement to torsional displacement
6 旋转薄壁圆环的自由振动
6.1 波的传递矩阵
波动从弯曲梁起始端向末尾端传播时,相位将改变、幅值将衰减.相位和幅值的改变与弯曲梁波导的波数和长度有关.波数和长度对波动的影响可以由传递矩阵来表示.从波模式可知,波数有正负之分.因此,正行波沿坐标系正方向传播θ角和负行波沿坐标系负方向传播θ角可以表示为如下形式:
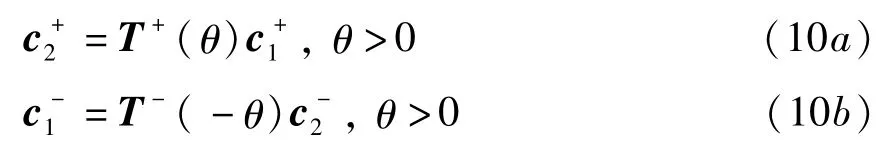
波的传递矩阵表示为:

6.2 正负行波的频率特征方程
由行波的相位封闭原理[3]可知,当入射波沿圆环传播经历一个波动循环,入射波之间的相位相差2π的整数倍时产生驻波,圆环系统发生共振.结构振动的模态(驻波)是由波幅相等且传播方向相反的波的叠加振型.结构发生共振时,正行波的波幅系数和负行波的波幅系数有如下关系:
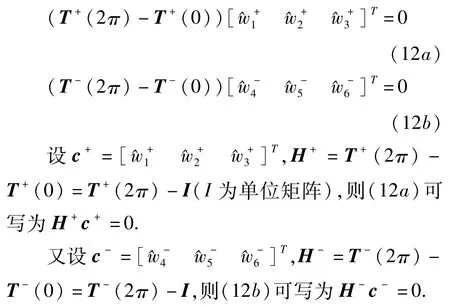
令|H±|=0,即圆环振动的特征方程.方程|H+|=0解得的固有频率对应的模态就是正行波在圆环传播形成的驻波,而方程|H-|=0解得的固有频率对应的模态是负行波在圆环传播形成的驻波.
6.3 具体算例
为了验证行波相位封闭原理求特征值的方法的有效性,以图1所示的等截面旋转薄壁圆环为例计算其固有频率.在算例中给定了圆环的几何尺寸和物理参数.弹性模量E=207GPa,剪切模量G=80GPa,泊松比v=0.3,半径R=0.1m,截面宽度b=0.002m,截面高度h=0.002m,密度ρ=7850kg/m3,转速Ω=500rad/s.
设特征函数f+=|H+|和f-=|H-|,波数代入矩阵H+和H-.用数值方法计算特征函数数值,得到特征函数曲线,然后搜索f+=0和f-=0对应的频率点,得到频率方程的解即振动固有频率.从f+=0得到正行波的固有频率,从f-=0得到负行波的固有频率.
图6是转速Ω=500rad/s时的行波特征函数曲线.其中,实线为幅值的模,虚线为实部,点划线为虚部.根据频率搜索的原理,上述实线为零时的频率值为频率方程的解,也就是旋转圆环的固有频率.表1所示的是旋转圆环前四阶固有频率.

表1 旋转圆环前四阶固有频率(rad/s)Table 1 Four natural frequency of rotating ring(rad/s)
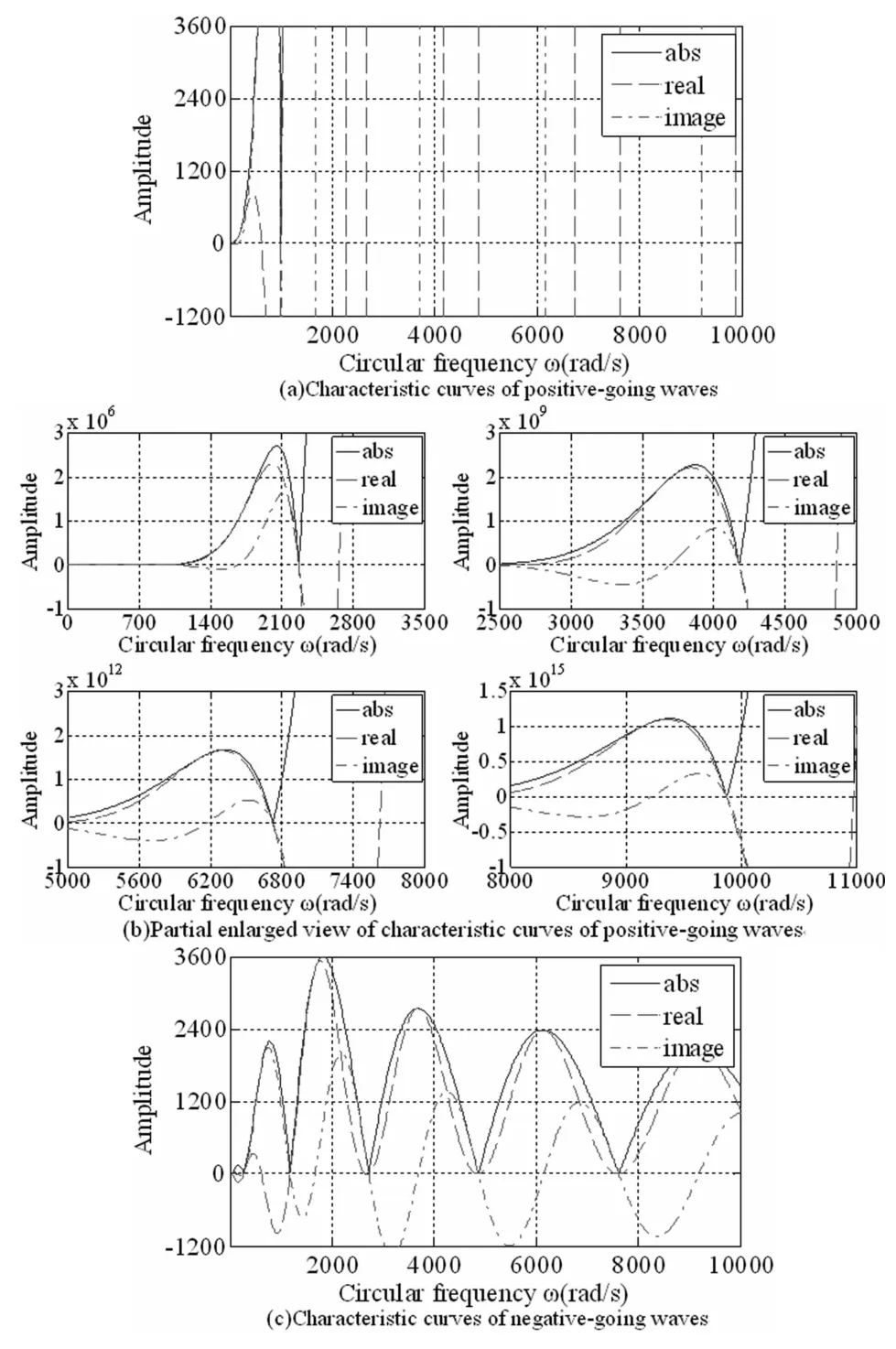
图6 平面外行波特征函数曲线Fig.6 Characteristic curves of out-of-plane wave
转速对圆环前四阶固有频率的影响如图7所示.从图7中可以看出:1)各阶固有频率在转速的影响下都出现了两个相异的频率值,即频率分支现象;2)正行波的固有频率随转速的增大而增大,而负行波的固有频率随转速的增大而减小;3)文中所得到的固有频率与文献[13]的结果一致.
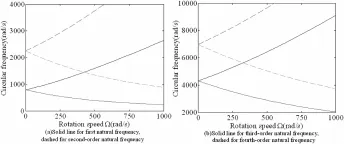
图7 平面外振动的固有频率Fig.7 Natural frequency of out-of-plane vibration
7 结论
行波法可以有效地解决旋转圆环平面外的振动问题,分析高速保持架自由振动以及行波特性,获得一些旋转圆环平面外行波振动特性:(1)静止圆环的正行波波数与负行波波数是相等的,构成对称波谱图,而旋转圆环的四种波模式与静止圆环的四种波模式是不相同,旋转圆环的波谱图也不对称;(2)在旋转圆环上,振动波的相速度不对称;(3)旋转圆环的截止频率会随着转速的增加而增加.行波法可以求得旋转圆环平面外振动的固有频率,以及固有频率随速度变化的规律.算例中,行波法求得的固有频率与其他文献的结果是一致的,验证行波法分析等截面圆环的自由特性是准确和有效的.
1 Mead D J.Waves and modes in finite beams:application of the phase-closure principle.Journal of Sound and Vibration,1994,171(5):695~702
2 Mei C,Mace B R.Wave reflection and transmission in Timoshenko beams and wave analysis of Timoshenko beam structures.Journal of Vibration and Acoustics,2005,127(4):382~394
3 Mei C.Wave analysis of in-plane vibrations of H-and T-shaped planar frame structures.Journal of Vibration and Acoustics,2008,130(6):061004~061010
4 Mei C.An analytical study of dynamic characteristics of multi-story Timoshenko planar frame structures.Journal ofDynamic Systems,2014,136(5):051004
5 Chouvion B,Fox C H J,McWilliam S,etal..In-plane free vibration analysis of combined ring-beam structural systems by wave propagation.Journal of Sound and Vibration,2010,329(24):5087~5104
6 Kang B,Riedel C H,Tan C A.Free vibration analysis of planar curved beams by wave propagation.Journal of Sound and Vibration,2003,260(1):19~44
7 Huang D,Tang L,Cao R.Free vibration analysis of planar rotating rings by wave propagation.Journal of Sound and Vibration,2013,332(20):4979~4997
8 Lee S Y,Chao J C.Out-of-plane vibrations of curved nonuniform beams of constant radius.Journal of Sound and Vibration,2000,238(3):443~458
9 Chouvion B,Popov A A,McWilliam S,et al.Vibration modeling of complex waveguide structures.Computers and Structures,2011,89(11-12):1253~1263
10 Eley R,Fox C H J,McWilliam S.Coriolis coupling effects on the vibration of rotating rings.Journal of Sound and Vibration,2000,238(3):459~480
11 蒋宝坤,李映辉,李亮.旋转粘弹性夹层梁非线性自由振动特性研究.动力学与控制学报,2013,11(3):241~245(Jiang B K,Li Y H,Li L.Vibration analysis of rotating viscoelastic sandwich beam.Journal of Dynamics and Control,2013,11(3):241~245(in Chinese))
12 周延泽,王春洁,陆震.高速滚动轴承保持架自由振动特性研究.北京航空航天大学学报,2001,27(5):596~599(Zhou Y Z,Wang C J,Lu Z.On the free vibration of high-speed ball bearing retainer.Journal of Beijing University of Aeronautics and Astronautics,2001,27(5):596~599(in Chinese))
13 Kim W.Free non-linear vibration of a rotating of a rotating thin ring with the in-plane and out-of-plane motions.Journal of Sound and Vibration,2002,258(1):167~178
14 Lee S K,Mace B R,Brennan M J.Wave propagation,reflection and transmission in curved beams.Journal of Sound and Vibration,2007,306(3-5):636~656
Received 15 September 2014,revised 20 October 2014.
*The project supported by the Shanghai industry-university-research cooperation program(CXY-2013-22)
†Corresponding author E-mail:hdishan@shu.edu.cn
OUT-OF-PLANE VIBRATION ANALYSIS OF A ROTATING THIN RING BY WAVE PROPAGATION*
He Hong Huang Dishan†
(School of Mechatronical Engineering and Automation,Shanghai 200072,China)
To solve the dynamic problem for the out-of-plane vibrations of a rotating thin ring,this paper studied the basic transmission characteristics of elastic wave propagation,and analyzed the dispersion equation,wave numbers,cut-off frequencies,phase velocity and the ratio of axial vibration displacement to torsional vibration displacement,which is valuable in the free vibration analysis of the solid cage in a high speed roller bearing.Based on the wave propagation method,the positive and negative wave numbers were separated by the criterion of positive-going waves.The characteristic equation of a rotating thin ring was established by the phase-closed principle and the transfer matrices.One example was given to solve the natural frequencies of the rotating ring,and the result is consistent with the result of the given literature.
out-of-plane vibration,rotating thin ring,wave propagation,wave number
10.6052/1672-6553-2014-081
2014-09-15收到第1稿,2014-10-20收到修改稿.
*上海市产学研合作计划(沪CXY-2013-22)
†通讯作者E-mail:hdishan@shu.edu.cn

