压电谐振驱动三足机器人的平面运动*

李魁 徐鉴

（同济大学航空航天与力学学院，上海 200092）

压电谐振驱动三足机器人的平面运动*

李魁 徐鉴†

（同济大学航空航天与力学学院，上海 200092）

设计并实现了一类利用压电陶瓷片作动，由三条曲梁足支撑的振动驱动机器人.建立了在一条足共振驱动下机器人水平运动的动力学方程，数值计算解释了摩擦作用下的运动机理，寻找到异性摩擦对运动方向、速度的影响和压电激励频率与运动速度间的关系.通过建立圆弧曲梁控制方程求解圆弧型足面内振动的固有频率及振型，设计了三组不同频率的圆弧曲梁足参数，实验制作了机器人模型，利用压电控制三足间振动的共振切换，实现了预想的三个方向的运动以达到平面运动的效果，实验测量了机器人的运动速度与理论计算吻合得较好.

机器人，压电，曲梁共振，摩擦，平面运动

引言

微型机器人的驱动形式和平面运动的控制正成为近些年的研究热点.Driesen［1］对已实现的微型运动机器人做了详细的分类，从结构和运动形式的角度可分为：轮式机器人、躯干行走机器人、尺蠖机器人、滑移式机器人、惯性冲击式机器人等.从驱动形式的能量转化出发可分为：机械能-机械能的转化，作动器常选用马达部件；电能磁场能-机械能的转化，多采用智能材料如电磁材料、压电材料等.但传统的运动机器人中的电机、传动机构等原件使得机器人结构形式十分复杂，微型化后组装十分困难且成本较高，近年来振动驱动系统的提出实现了结构简单、可封装一体化的优点.Chernous’ko［2］和方虹斌［3］提出了内部质量块两相、三相控制的振动驱动系统并对运动速度进行了优化.占雄［4］利用内部质量块的二维三相控制实现了振动驱动系统的平面运动.Lobontiu［5］从结构简便、节省能量的角度提出了弹性振动移动系统的理念，利用弹性体的振动变形与外界环境作用实现机器人的运动，Minch-Robot原型［6］体现了这种想法，它利用矩形压电双晶片带动两条非对称足振动，控制压电作动频率在两足的共振范围内相互切换实现了向左和向右偏移的运动.Becker利用圆形压电片作动制作了可在陆地和水面运动的两栖机器人［7-8］，通过改变驱动频率实现平面运动，但运动方向较为任意，无法控制定向运动.Pan［9］使用两片压电双晶梁作动，调节压电电压相位可控制机器人的直线运动和转向.李伟达［10］设计了一种基于跳变电压下粘滑运动和简谐电压激励下碰撞运动的复合驱动机器人，利用碰撞模型解释了驱动原理，实现了高运动分辨力和较快的运动速度，但只能实现直线运动.然而，大量此类弹性振动驱动的研究在作动方式的尝试、从概念的角度利用共振制作机器人原型的阶段，建立移动机器人动力学模型解释共振运动机理和定量分析的研究还相对较少.

本文根据［5］中弹性变形振动驱动的思路，通过压电材料对弹性体作动，利用共振对振动变形的放大作用，提出了一种结构简单的压电作动谐振式运动系统，考虑了机器人足端在压电板的激振作用下与地面的摩擦作用，数值计算分析了异性摩擦对运动方向和速度的影响，并建立曲梁控制方程计算圆弧型足的固有频率，根据所设计的三组足参数研制了三足机器人，通过调节压电作动频率实现了三个方向运动的切换.

1 机器人实物原型

本文提出的三足谐振式振动驱动机器人原型如图1所示，该机器人由两部分结构构成：结构一为粘结有圆形压电作动片的圆形铝板组成的机器人身体；结构二为特定曲率圆弧形金属丝制作的机器人足，足一端与身体固支另一端与地面接触.其中，身体的作用是在压电片作动下产生变形，在边界与足固支处将振动传递到机器人的足上，机器人足在振动变形过程中与地面接触，系统整体在地面摩擦作用下实现运动.

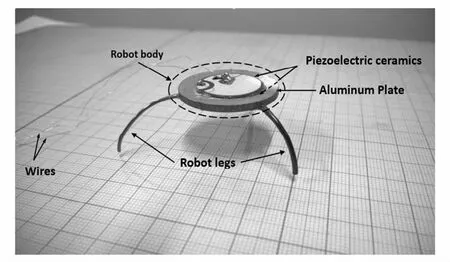
图1 三足机器人原型Fig.1 Prototype of three-legged robot

2 圆弧足机器人动力学方程

本文中机器人的身体结构如图1所示，中间为圆形铝板，上下两层粘贴有压电陶瓷片，极化方向为上下两侧法线方向，采用串联式接法，上下两层压电片的变形相反，即上层伸长下层缩短，身体圆形铝板产生弯曲变形，在圆板边界足端固支处对机器人足作用交变转角激励，设为φ（t）＝εφcosΩt，其中εφ为微转角幅值，Ω为压电驱动频率.

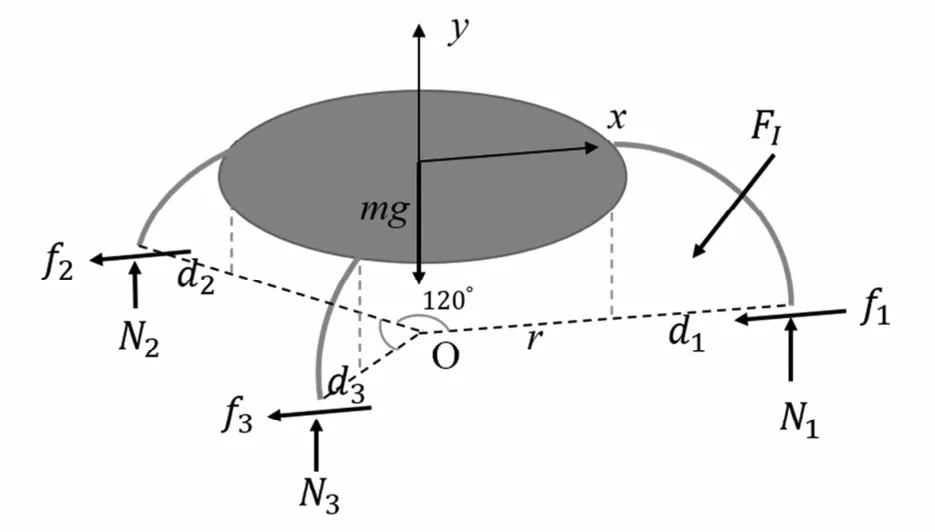
图2 机器人简化力学模型Fig.2 Simplified mechanical model of the robot

如图2，考虑机器人三足不同几何尺寸使得固有频率不同，足为圆弧曲梁，足端垂直地面放置，圆板半径r.压电作动频率在其中一条足的共振频率附近时，由于压电体在较高激励频率下变形一般在微米量级，根据共振理论的分析可知，该条足的振动幅值亦十分微小但会明显高于另两条支撑足，此时机器人在该条足的驱动下实现运动.模型中考虑该足微幅振动惯性力FI，则地面在三足处的支持力Ni以及摩擦力fi（i＝1，2，3）也会不同，如图2所示.利用机器人整体的力系平衡条件可得：

式中，FIx和FIy为惯性力分量，MI为惯性力对O点取矩.

碰撞会产生非常复杂的非线性行为［11］，在频率为kHz量级的压电激振下圆板变形很小，且由梁变形理论可知曲梁环向相对径向位移可以忽略，可以认为足端始终没有离开地面，因此仅考虑圆弧足与地面间的滑移，忽略与地面间的碰撞，机器人不存在跳跃现象，近似认为¨y＝0恒成立，代入（1）后两式解得：

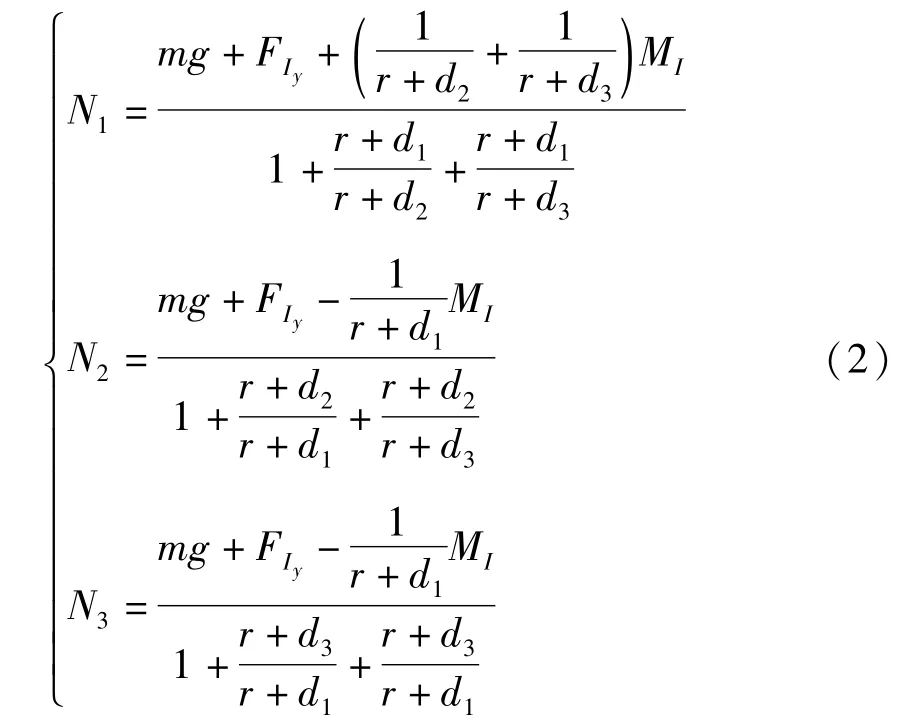
方程组（1）第一式中x（t）即为机器人的水平位移，可以看出该动力系统是在圆弧足振动惯性力水平分量和摩擦力的作用下实现的运动，因此我们需要对圆弧足建模，进而求解足的振动与机器人水平运动的耦合方程组，得到所关注的机器人位移x（t）.

根据圆板变形对圆弧足的转角激振作用，将圆弧足简化为一端固支一端自由的细长悬臂曲梁，坐标系建立如图3（a）所示，利用Newton方法可得曲梁微元体平衡方程：

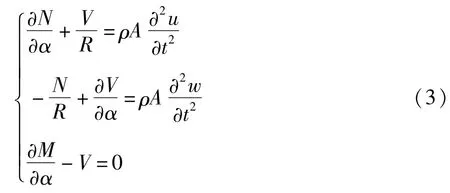
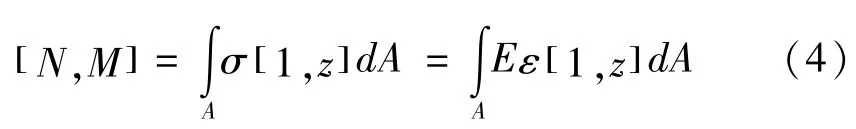
将ε0与χ代入上式积分可得：

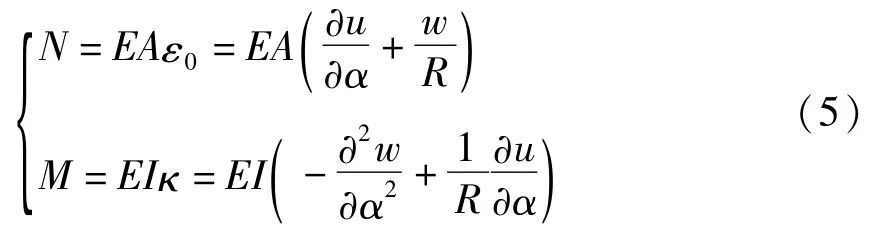
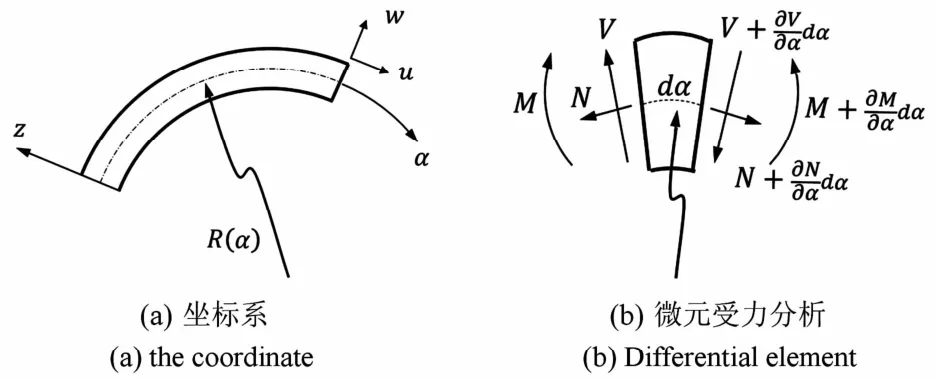
图3 曲梁Fig.3 Curved beam

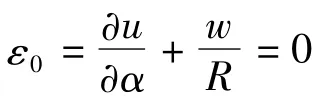
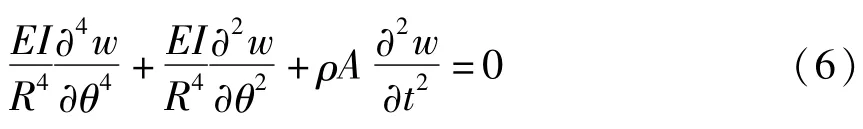
边界条件为：

（6）式中第二项由曲梁曲率引起，若曲率半径R趋于无穷大，则该项趋于零，方程退化为直梁振动方程，也从方程退化的角度验证了我们曲梁建模的正确性.

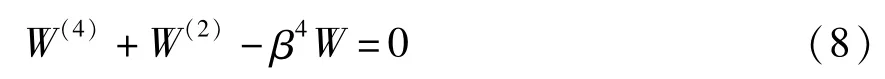
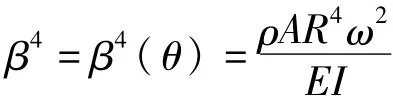
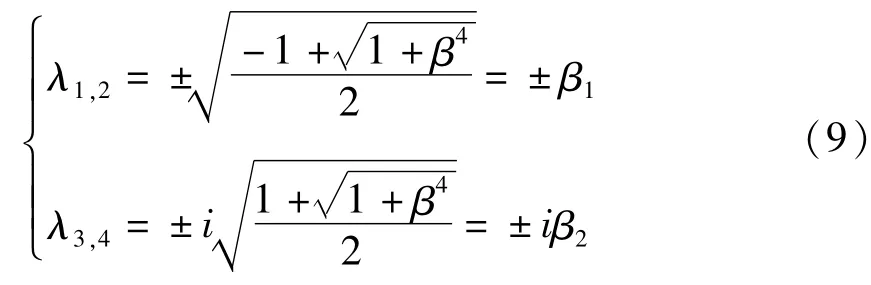
故主振型W（θ）的通解表达式可以写作：

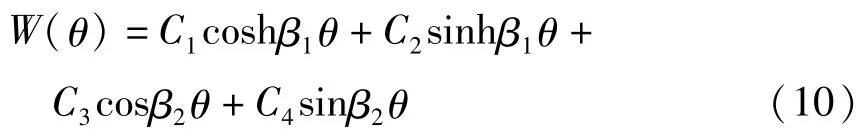
将（10）式代入边界条件（7）令其系数行列式为零，即可解得悬臂曲梁各阶固有频率ωi及振型解析表达式Wi（θ）.

现考虑圆弧足在固支端转角激励以及自由端地面摩擦力作用下的受迫振动.由几何关系易知，固支端转角引起的曲梁径向位移wg＝Rsinθφ（t），引入变换w*＝w-wg代入（7）式，并在曲梁自由端引入摩擦力f1，可得（为书写简便仍用w代替w*）：

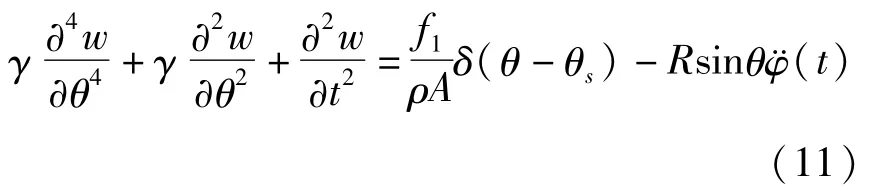
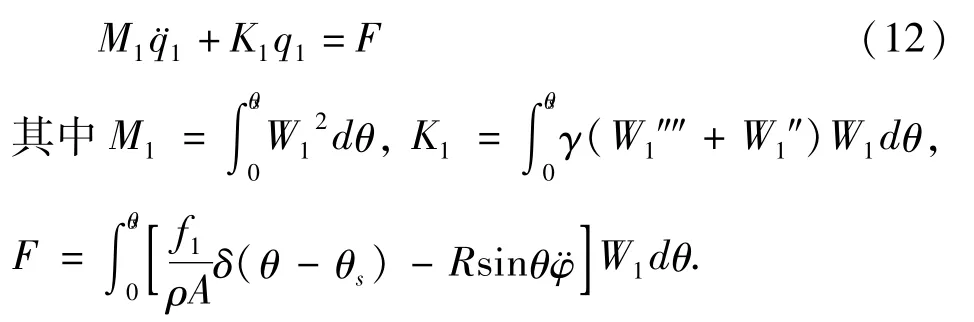
联立（1）第一式以及（12）式，组成以机器人水平位移x（t）和圆弧曲梁足一阶模态坐标q1（t）为待求函数的耦合方程组，可得：

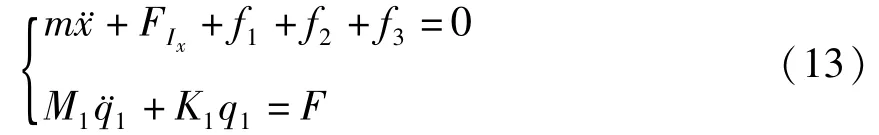
其中，FIx，FIy，MI的具体表达式可写作（14）：

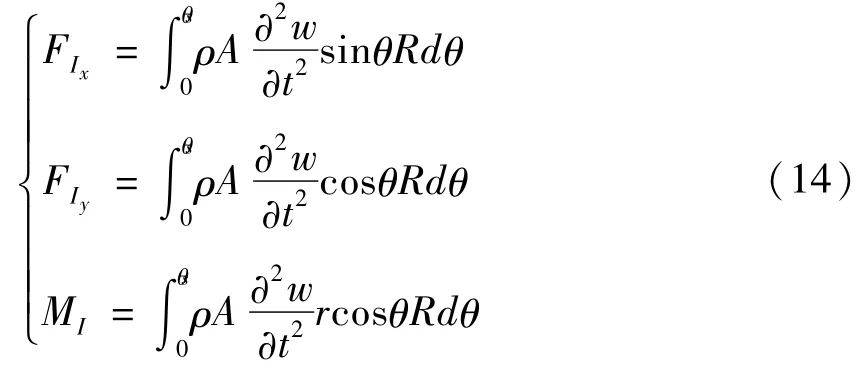
在本文中考虑的摩擦形式为库伦摩擦，f1，f2，f3的表达式如下式所示：

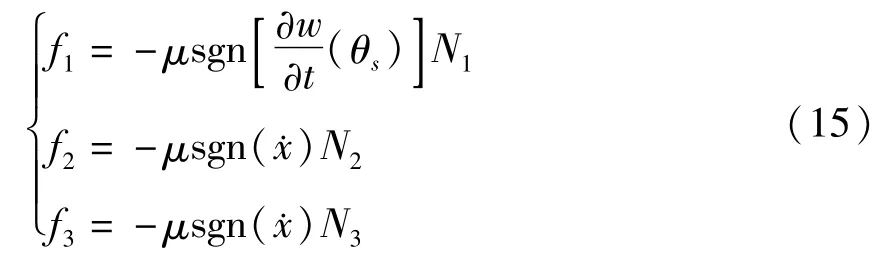
式中，sgn为分别关于驱动足足端振动速度、机器人水平运动速度的符号函数.

将（2）、（14）、（15）式代入系统耦合方程组（13），引入曲梁一阶阻尼比ξ1，利用状态变量变换，化简得方程组（16）：

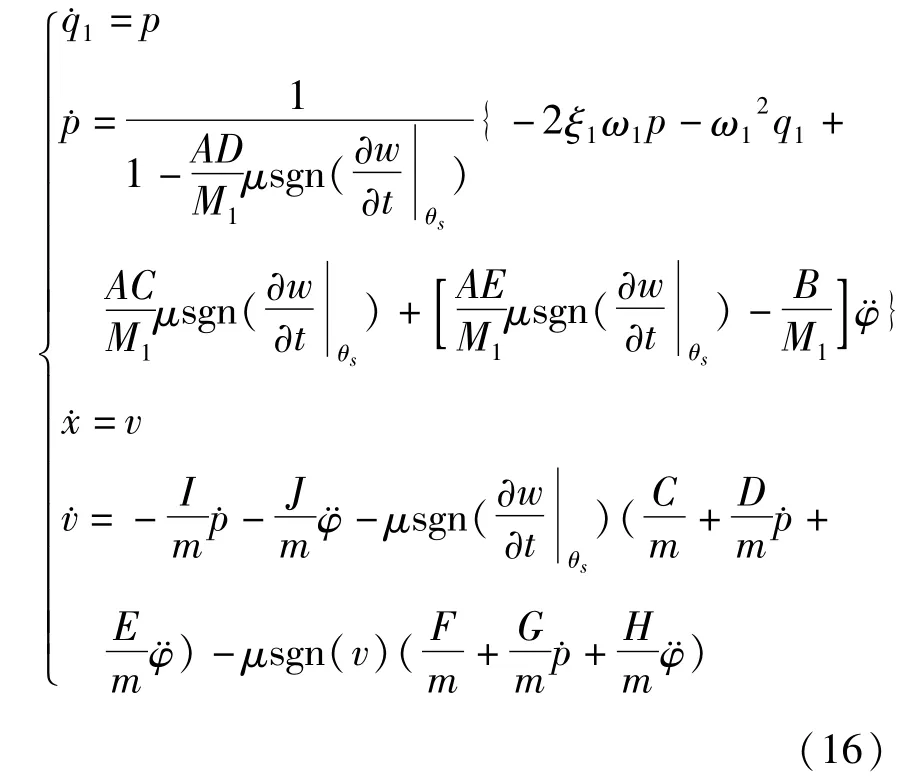
式中，A，B，C，D，E，F，G，H，I，J均为积分常数.由于库伦摩擦中符号函数存在阶跃性，状态方程组（16）的解析解无法得出，下一小节中将利用四阶龙格-库塔法数值求解得到机器人位移.

3 数值求解及运动机理

根据上文所述的机器人身体圆板弯曲变形对圆弧足的转角激励为φ（t）＝εφcosΩt，但转角幅值无法根据测量给出，本小节首先利用有限元分析软件ANSYS（Mechanical APDL 14.5）仿真计算近似确定圆弧足固支端转角量级.

本文中选用的压电材料为PZT-5，其压电体介电常数矩阵、压电体劲度系数矩阵以及压电应力常数矩阵参照IEEE标定标准（z方向极化）.压电体选用SOLID5单元建模，压电片上下两层银电极通过上下两层位置的单元节点耦合电压实现等电位，圆形铝板选用SOLID45单元建模，根据实际测量，压电薄片半径20mm，厚度0.42mm，圆形铝板半径30mm，厚度2mm，网格划分如图4（a）.正弦压电驱动频率为1100Hz，电压幅值为120V.

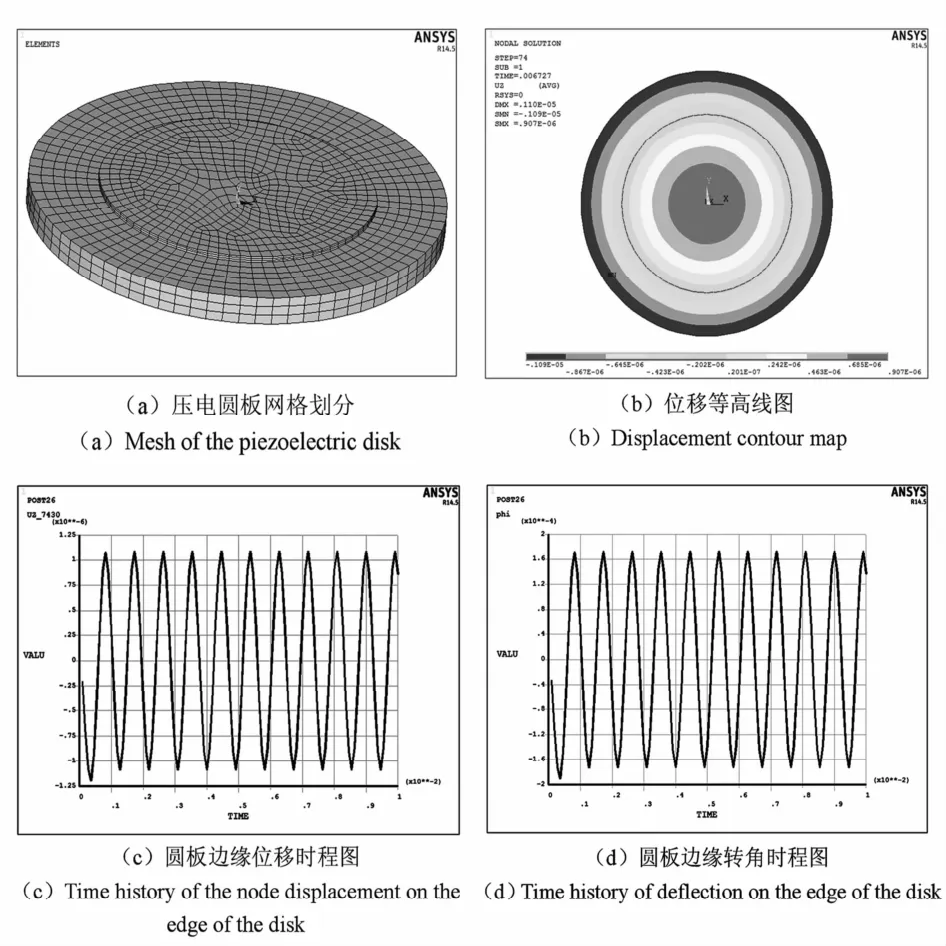
图4 机器人圆板压电作用下变形仿真计算Fig.4 Deformation simulation of robot body excited by piezoelectric actuator

根据ANSYS瞬态分析仿真计算结果可知，由于机器人身体几何外形轴对称，压电体施加的等效荷载也是轴对称的，因此身体在压电体作动下变形等高线图呈轴对称分布，如图4（b），圆板边缘处一周位移相等、转角相等.取边界处任意一节点位移时程如图4（c）所示，位移幅值为1.1×10-6m，即在压电高频激励下板的振动位移为微米量级.边缘处转角如图4（d），转角幅值也十分微小，弧度制为1.7×10-4，即10-2角度量级.因此，根据仿真计算结果可知，在数值求解圆弧曲梁振动与机器人位移耦合方程组（16）时曲梁固支端转角激励幅值取为10-4量级是较为合适的.计算参数选取如表1所示，该组圆弧曲梁足设计参数下，利用上一小节中推导的圆弧曲梁固有频率计算得到一阶固有频率为1107 Hz.

表1 数值计算参数Table 1 Parameters of numerical Simulation

首先考虑系统在压电作动下库伦摩擦对运动的影响，激励频率在曲梁一阶共振点附近，为1100Hz.图5（a）的数值计算结果表明，在地面绝对光滑无摩擦情况下，系统水平方向不受外力，机器人在足振动惯性力作用下，在原点附近往复振动无法实现定向运动.在异性库伦摩擦作用下，双向摩擦因数的相对大小决定了机器人的运动方向，系统朝库伦摩擦因数小的方向实现定向运动，如图5（b）所示.图5（c）计算了多组不同异性摩擦下机器人的运动位移，结果表明在异性摩擦的定向驱动下，两个方向的摩擦系数差异越大，即摩擦的非对称越明显，机器人运动速度也就越快.

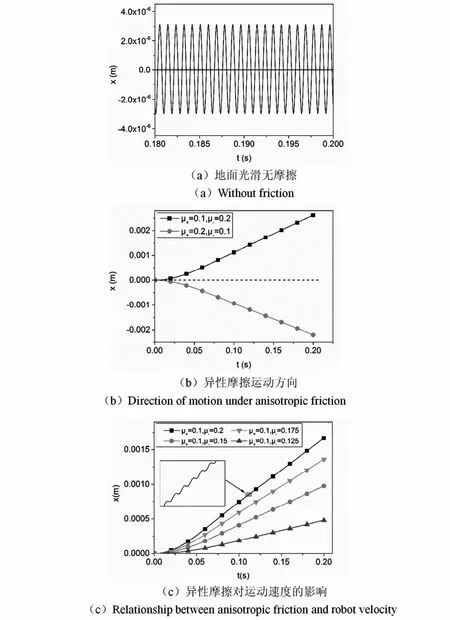
图5 库伦摩擦作用下运动情况Fig.5 Effects of Coulomb friction respect on robot locomotion

为了进一步研究曲梁振动频率对运动速度影响，在共振频率点附近选择不同的激励频率对系统作动，以最大速度归一化后的机器人运动速度如图6所示.计算结果说明不论异性库伦摩擦形式如何，压电激振频率总是越靠近圆弧足共振频率，机器人移动得越快，即机器人速度在足共振频率点附近达到最大值.根据图5（c）中的局部放大图可知，机器人运动可分解为振动位移和移动位移，直观地理解，圆弧曲梁足在共振点附近受迫振动时，由于共振对振动的放大作用，足与地面在一个周期内受到地面的摩擦的作用越大，由摩擦产生的移动位移越大，N个周期累积后使得机器人移动得越快.计算结果验证了我们利用弹性足共振驱动，在节省能量的同时达到较快运动速度的设想.利用共振点激励下机器人运动速度会明显高于非共振点这一结论，在谐振机器人的实验研制中我们设计了三组不同参数达到不同共振频率的曲梁足，利用每一根足的共振驱动实现三个方向的运动切换的效果，从而实现平面运动.

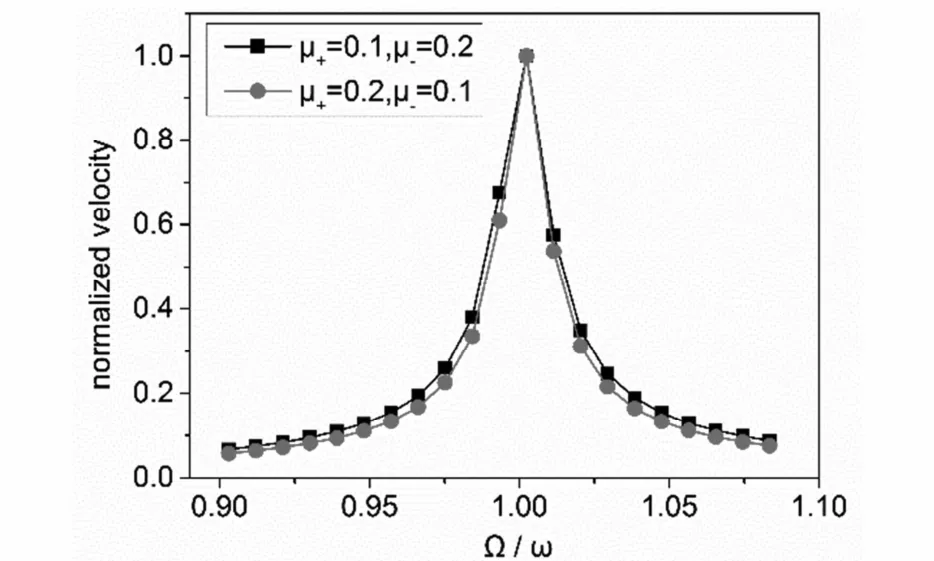
图6 不同激励频率下的速度Fig.6 Velocity-frequency curves

4 三足机器人实验研究

为了通过实验验证上文中所阐述的利用机器人足谐振驱动下的机器人运动，实现在三条足间共振切换使得机器人朝三条足各自的方向运动的设想，我们研制了如图1中所示的三足谐振驱动机器人，身体直径3cm，总质量为6.5g，机器人运动表面材质为玻璃.根据第二小节建立的曲梁振动方程的求解，设计机器人原型的三组足特征参数如表2所示，这三条足的一阶固有频率分别在1100Hz、2500Hz、4000Hz附近.机器人实验装置如图7所示，利用信号发生器（型号为：RIGOL-DG1022）生成正弦信号，将此信号输入压电陶瓷驱动电源（型号为：HPV-3C0150A0300D）模拟输入端，压电陶瓷驱动电源对信号进行15倍放大后对机器人身体上的压电作动片施加正弦电压信号.

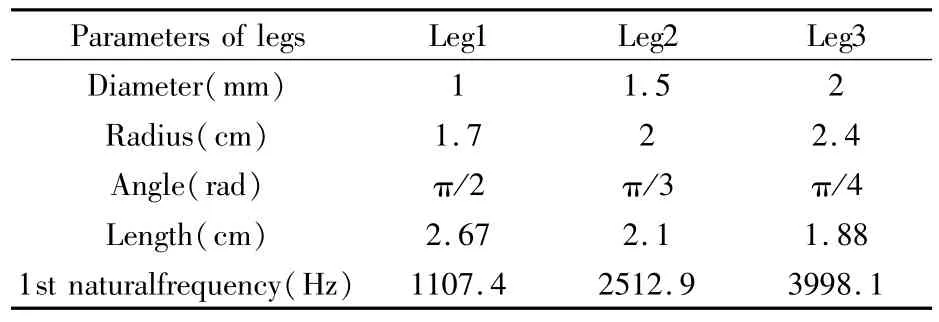
表2 机器人足参数Table 2 Leg parameters of robot prototype

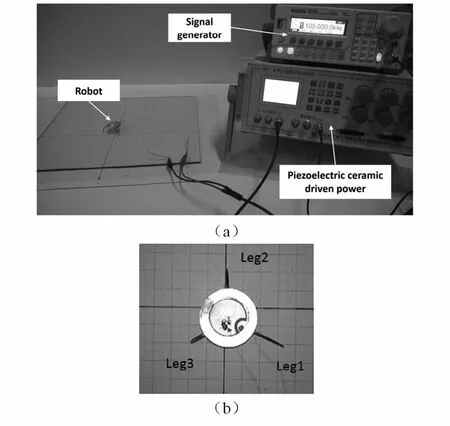
图7 三足机器人实验：（a）实验装置图，（b）机器人足编号Fig.7 Three-legged robot experiment：（a）Experimental set-up，（b）Serial number of robot legs

当压电片驱动电源信号频率为1100Hz时，可知由于激励频率在1号足一阶固有频率附近，因此1号足的振动幅值会明显高于另两条足，表现为Leg1振动驱动，从摄像机拍摄机器人运动视频中截取不同时刻的位移如图8（a）所示.实验中利用测力计测得沿三条足各自前后方向的摩擦系数近似值分别为：Leg1前后两方向μ+＝0.3335，μ-＝0.3876；Leg2前后两方向μ+＝0.3612，μ-＝0.3494；Leg3前后两方向μ+＝0.3412，μ-＝0.3653.按照上一小节数值计算结果表明机器人会朝着摩擦因数小的方向前进，即沿着Leg1正方向前进.同理，另外两条足振动驱动下应沿着Leg2负方向前进和Leg3正方向前进.实验拍摄记录如图8（a）、（b）、（c）所示，运动方向与我们的理论分析一致，从而验证了模型及数值计算的正确性.

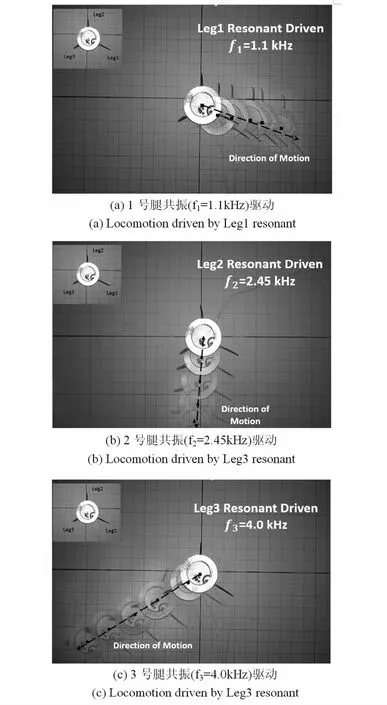
图8 机器人运动方向切换Fig.8 Direction shift

实验中由于机器人足端异性摩擦难以定量实现，我们利用斜面等效异性摩擦的方法来验证异性摩擦对运动速度的影响.在水平表面Leg1前后方向异性摩擦为μ+＝0.3335，μ-＝0.3876，将机器人分别放置在角度为2.81°、4.16°、5.56°的斜面上，由于沿斜面方向重力分量的作用，使得异性摩擦得以等效实现，分别为（a）μ+＝0.3825，μ-＝0.3386；（b）μ+＝0.4061，μ-＝0.3150；（c）μ+＝0.4303，μ-＝0.2908.施加正弦压电电压频率为1100Hz，电压峰峰值幅值为225V，此时激发Leg1的共振，利用Polytec（型号为：PSV-400）激光测振仪测量机器人在斜面上运动的运动速度和位移.图9为上述等效异性摩擦作用下机器人运动位移实验测量和数值计算的对比图，在异性摩擦的作用下理论预测的机器人运动方向与实验结果定性一致，且运动速度定量上也相对吻合.实验表明异性摩擦的确可以控制机器人的运动方向，使得机器人朝着摩擦较小的方向前进，而前后方向摩擦异性差异越大运动速度也就越快.

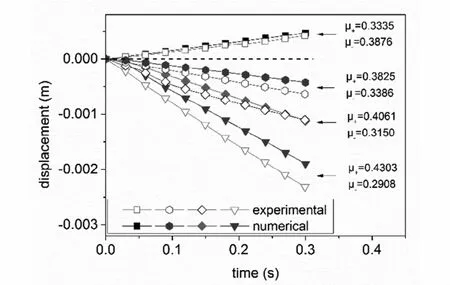
图9 异性摩擦对运动方向和速度的影响实验理论对比Fig.9 Experimental and numerical resultsof the effect of anisotropic friction

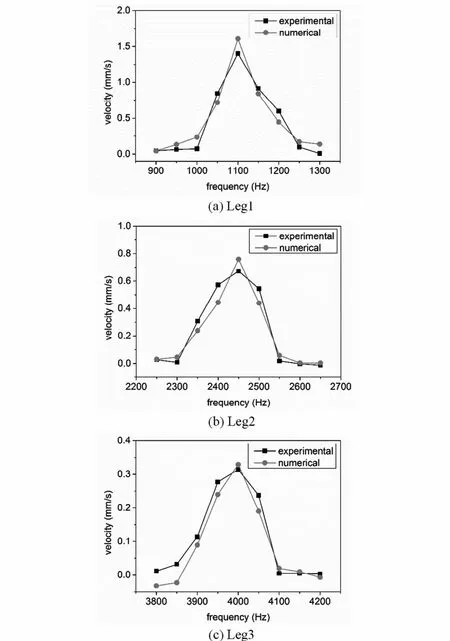
图10 三足振动驱动时频率与运动速度的关系Fig 10 Frequency-velocity relationships of leg vibration-driven robot

正弦压电频率在Leg1共振频率附近间隔取值，保持驱动电压幅值恒定为112.5V，激光测量机器人的运动速度与数值计算对比如图10（a）所示，从实验结果中可以发现在激励频率越靠近机器人足的共振频率运动速度越快，且在共振点附近达到速度最大值，实验测量得到的机器人运动速度与驱动频率关系与理论计算定性吻合.由于实验中拉力计测量滑动摩擦系数与实际存在一定误差，在数值计算中对异性摩擦测量值作微调得到得的机器人运动速度与实验测量值定量上也吻合得较好，验证了上一小节的理论分析，说明了模型的正确性.在另外两组实验中，Leg2和Leg3共振驱动下也得到了相同的结论，如图10（b）和10（c）所示.

5 结论

本文设计了一种结构十分简单的微小型机器人，实验研制了机器人原型样机，从理论和数值两个方面分析了其运动机理，通过数值计算、实验验证得到了以下结论：

（1）建立机器人考虑足弹性振动、系统摩擦力作用下的力学模型，数值计算结果说明圆弧足振动惯性力引起振动位移，而驱动机器人前进的是摩擦力的作用.异性库伦摩擦可实现定向运动，且异性摩擦差异越大运动速度越快.

（2）机器人身体激发圆弧足共振时，系统水平方向运动速度明显高于其他频率.推导得出了曲梁面内振动的频率计算公式及模态函数，设计了三组不同频率的足参数，利用三条足间共振切换达到三足分别驱动的效果，实现了机器人三个方向的运动.

（3）实验测量和数值计算吻合较好，验证了异性摩擦对机器人运动方向和运动速度的影响，以及在机器人足共振点附近激振可实现最大运动速度的结论.

1 Driesen W.Concept，modeling and experimental characterization of the modulated friction inertial drive（MFID）locomotion principle-application to mobile microrobots［PhD Thesis］.Lausanne：Swiss federal Institute of Technology in Lausanne，2008

2 Chernous′ko F L.Analysis and optimization of the motion of a body controlled by means of a movable internal mass.Journal of Applied Mathematics and Mechanics，2006，70（6）：819～842

3 FangH B，Xu J.Dynamic analysis and optimization of athree-phase control mode of a mobile system with an internal mass.Journal of Vibration and Control，2011，17（1）：11～17

4 Zhan X，Xu J.Locomotion analysis of a vibration-driven system with three acceleration-controlled internal masses.Advances in Mechanical Engineering，2015，doi：10.1177/1687814015573766

5 Lobontiu N O，Gordon M K，Fisher G，et al.Design and analysis of elastodynamic locomotion for robotic insects.In：Sulzmann A，Nelson B J eds.Microrobotics and Micromanipulation，Proceedings SPIE 3519，Boston，1998：118～127

6 Zimmermann K，Behn C，Zeidis I.Mechanics of terrestrial locomotion：with a focus on non-pedal motion systems.Heidelberg，Springer-Verlag，2009：269～273

7 Becker F，Minchenya V，Zimmermann K，et al.Single piezo actuator driven micro robot for 2-dimensional locomotion.In：Ananthasuresh G K，Corves B，Petuya V eds.MicromechanicsandMicroactuators，Proceedingsof MAMM 2010，Aachen，2010.Netherlands：Springer，2012：1～10

8 Becker F，Zimmermann K，Volkova T，et al.An amphibious vibration-driven microrobot with a piezoelectric actuator.Regular and Chaotic Dynamics，2013，18（1-2）：63～74

9 Pan C H，Tzou S S，Shiu R Y.A novel wireless and mobile piezoelectric micro robot.In：Mechatronics and Automation（ICMA），Proceedings of the IEEE International Conference on Mechatronics and Automation，Xi＇an，2010：1158～1163

10 孙立宁，李伟达，蒋振宇，等.一种单构件双运动机理微小型机器人移动机构.机器人，2010（1）：41～47（Sun L N，Li W D，Jiang ZH Y，et al.A single component locomotion mechanism with dual driving principles for micro and miniature robot.Robot，2010（1）：41～47（in Chinese））

11 边菁，徐鉴.悬臂梁限位器非线性动力学效应实验分析.动力学与控制学报，2015，13（2）：144～153（Bian J，Xu J.The experimental analysis of the nonlinear dynamics in a cantilever system with the stopper.Journal of Dynamics and Control，2015（2）：144～153（in Chinese））

Received 4 June 2015，revised 15 June 2015.

*The project supported by the National Natural Science Foundation of China（11272236）

†Corresponding author E-mail：xujian@tongji.edu.cn

LOCOMOTION OF THREE-LEGGED VIBRATION-DRIVEN ROBOT USING PIEZOELECTRIC ACTUATOR*

Li Kui Xu Jian†
（The School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China）

A three-legged resonant vibration driven robot using piezoelectric actuator is presented in this paper.The dynamical equations of the horizontal locomotion is established as one of the three legs vibrating in resonant condition.Numerical results illustrates the motion mechanism and the effect of anisotropic friction on direction and velocity of the robot.The approximate relationship between the frequency of piezoelectric actuator and the velocity of locomotion is obtained.The governing equation of in-plane vibration for a curved beam is developed to calculate the natural frequencies and the corresponding mode shapes.Based on this equation，three sets of geometrical parameters for the curved legs are devised.It is found that their frequencies are respectively different.The robot prototype is also created according to these parameters.The planar locomotion is accomplished through robot testing by switching the frequencies of alternating voltage applied on piezoelectric actuator to the shift resonant among the legs.Experimental results reasonably match with the numerical simulation.

robot，piezoelectric actuator，curved beam resonant，friction，planar locomotion

10.6052/1672-6553-2015-064

2015-06-04收到第1稿，2015-06-15收到修改稿.

*国家自然科学基金资助项目（11272236）

†通讯作者E-mail：xujian@tongji.edu.cn