基于有限元法的波纹曲梁结构振动特性研究
王京军 邱 岳*
(1、中车青岛四方机车车辆股份有限公司,山东 青岛 266111 2、中车工业研究院(青岛)有限公司,山东 青岛 266071)
波纹曲梁结构作为一种典型工程结构零部件,具有轻质、高耐压强度和变形小等优点,广泛应用于桥梁、交通运输和船舶等工程领域。波纹曲梁结构的振动特性将严重由其组成整体结构振动性能,因此有必要对波纹曲梁结构开展振动特性分析,为波纹曲梁结构的结构优化设计提供理论基础。国内外许多学者已经对波纹曲梁相关结构开展了深入研究,并取得了一系列成果。
宁曙东基于铁木辛柯梁理论和欧拉- 伯努利方程,采用瑞丽- 里兹法开展曲率梁结构的面内自由振动特性研究[1]。赵雪健采用动刚度法研究平面曲梁结构的面内外振动特性,计算曲梁频率和振型[2]。李星照等人基于欧拉- 伯努利梁理论,建立圆弧曲梁结构的自由振动微分方程,开展曲梁结构自由振动特性研究[3-4]。孙广俊等人采用微分求积法建立曲线梁结构振动分析模型,研究曲线梁结构的振动特性[5]。叶康生等人采用p 型超收敛算法对平面曲梁面外自由振动问题进行求解[6]。谢臻等人基于Timoshenko 梁理论,采用无网格法和哈密尔顿原理,对曲梁结构开展自由和受迫振动特性分析[7]。陈明飞等人基于一阶剪切变形理论,采用等几何有限元法对变曲率功能梯度曲梁开展自由振动分析[8]。Ramon 等人基于薄厚曲梁理论,采用广义/扩展有限元法对曲梁结构开展面内自由振动特性分析[9]。Samira 等人采用半解析法和有限元法对变截面复合曲线梁结构开展振动特性分析[10]。
综上所述,现有研究主要是针对曲梁结构展开的,对波纹曲梁结构的研究较少。首先本文拟基于厚曲梁理论,采用有限元法和罚函数法建立一般边界条件下波纹曲梁结构振动特性分析模型;紧接着确定惩罚因子取值并将本文模型求解结果与有限元软件计算结果进行对比,开展模型验证;最后对波纹曲梁结构振动分析模型开展参数化研究,研究几何参数对波纹曲梁结构固有频率的影响,为波纹曲梁结构优化设计和减振降噪设计提高理论基础和技术指导。
1 理论推导
1.1 波纹曲梁结构模型介绍
如图1 所示,为波纹曲梁结构的几何模型示意图。波纹曲梁结构是由不同弧度曲梁结构通过共节点的方式耦合而成。图1 中αi(i=1,2,3,4,5)表示曲梁结构的弧度角,且2α1=α2=α3=α4=2α5。为了方便起见,采用曲线坐标系zs 对曲梁结构进行描述,考虑三个方向的自由度,其中ui、wi和θi分别表示切向位移、径向位移和转角位移;曲梁结构的截面为矩形截面,b 和h 分别表示截面宽度和截面厚度;R 表示曲梁半径。

图1 波纹曲梁结构示意图
1.2 波纹曲梁结构模型建立
根据厚曲梁单元理论,曲梁结构上任意一点的应变与位移存在如下所示的线性关系:

式中εi、χi和γi分别表示拉伸应变、曲率变化和剪切应变。根据材料的本构方程,曲梁结构上任意一点应力和应变存在如下所示关系。

式中ρ 表示密度;Li表示曲梁结构弧长长度;“·”表示对时间t 的导数。根据有限元的基本理论,曲梁结构的位移场函数可以写成如下形式:

式中Pj、Qj和Jj分别表示与ui、wi和θi有关的位移形函数,其具体表达式见文献[9];uj、wj和θj分别表示与ui、wi和θi有关的有限元节点自由度;n 表示单元节点个数;P、Q 和J 分别表示由位移形函数组成的矩阵。将式(1)、(2)、(3)和(5)带入式(4)进行化简可得。

式中Ki和Mi分别表示曲梁结构的刚度矩阵和质量矩阵,qi表示曲梁结构有限元节点在各个自由度方向位移组成的列向量。由于波纹曲梁结构是由不同弧度的曲梁结构通过有限元共节点的形式耦合而成,所以波纹曲梁结构的整体刚度矩阵和质量矩阵可以通过不同弧度曲梁结构的刚度矩阵和质量矩阵累加得到。在进行累加之前,应当对曲梁结构的刚度矩阵和质量矩阵进行维度扩展,使得曲梁结构的矩阵维度和波纹曲梁结构的矩阵维度相同。波纹曲梁结构刚度矩阵和质量矩阵可以写成如下形式:

式中S 表示惩罚因子,惩罚因子的取值可通过收敛性研究来确定。C 表示约束矩阵,其结构具体形式是通过约束有限元节点位移在整体有限元节点位移中的位置来确定的,是一个对角矩阵。当有限元节点位移被约束时,C 矩阵中对应的对角线元素取值为1,否则为0。根据上述得到的刚度矩阵和质量矩阵,波纹曲梁结构自由振动分析的运动方程可以写成如下形式。

式中ω 和φ 分别表示系统特征频率和特征向量,该式可以用于开展波纹曲梁结构自由振动特性研究。
2 算例分析
2.1 惩罚因子取值分析
由上所述,本文采用罚函数对波纹曲梁结构施加边界条件。为了确定惩罚因子的取值,本节研究波纹曲梁结构固有频率随惩罚因子的变化规律,具体如图2 所示。

图2 波纹曲梁结构固有频率随惩罚因子的变化规律
从图2 可以看出,波纹曲梁结构前三阶固有频率随着惩罚因子的增加呈现先增加后保持不变的变化趋势。为了保证模型的求解精度,惩罚因子取值为S=1011。为了便于后续模型求解,给出波纹曲梁结构边界条件的定义:
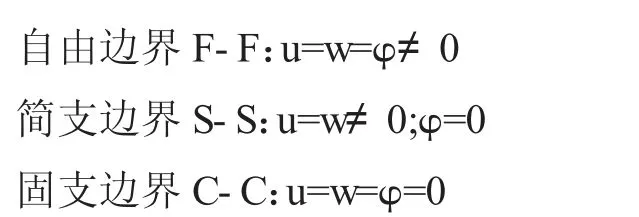
2.2 模型有效性验证
由上所述,本文已经建立了波纹曲梁结构自由振动特性分析模型。为了便于后续开展自由振动特性分析,本节对已建立波纹曲梁结构自由振动特性分析模型有效性开展模型验证。模型有效性验证主要包含两部分,分别是曲梁结构自由振动特性分析模型有效性验证和波纹曲梁结构自由振动特性分析模型有效性验证。模型有效性验证的具体措施是将本文模型的求解结果有限元软件求解结果进行对比验证。
首先开展曲梁结构自由振动特性分析模型有效性验证,将本文模型求解结果分别与有限元软件ABAQUS和ANSYS 软件计算结果进行对比,对比结果如表1 所示。同时指出,曲梁结构模型参数为:E=2.1e11Pa;v=0.3;b=h=0.001m;R=0.5m;α=60°。

表1 曲梁结构模型的固有频率对比验证
从表1 不难看出,在不同边界条件下,本文模型求解得到的前五阶固有频率与有限元软件的计算结果具有较好的一致性。紧接着,开展波纹曲梁结构自由振动分析模型有效性验证,对比结果如表2 所示。同时指出,波 纹 曲 梁 结 构 模 型 参 数 为:E=2.1e11Pa;v=0.3;2α1=α2=α3=α4=2α5=90°;b=h=0.01m;R=0.5m。

表2 波纹曲梁结构模型的固有频率对比验证
从表2 不难看出,在不同边界条件下,本文模型求解的前五阶固有频率与有限元软件求解结果在总体趋势上具有较好的一致性,但是个别阶数存在较大误差。根据上述模型对比结果,本文模型能够求解波纹曲梁结构在不同边界条件下的自由振动特性。
2.3 模型参数化研究
由上所述,本文模型有效性已经得到验证,可以用于分析波纹曲梁结构在一般边界条件下的自由振动特性。本节将通过研究波纹曲梁结构几何参数对其在简支边界条件下自由振动特性的影响来开展波纹曲梁结构自由特性分析。
首先研究厚度对波纹曲梁结构固有频率的影响,具体结果如图3 所示。除了厚度h 以外,其余模型参数与表2 中所用的模型参数相同。
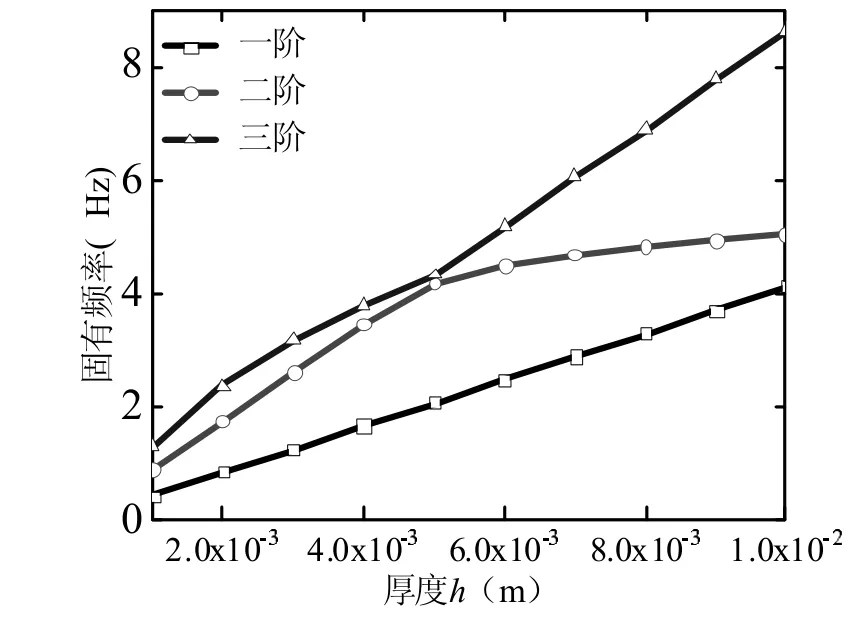
图3 波纹曲梁结构固有频率随厚度的变化规律
从图3 可以看出,在简支边界条件下,波纹曲梁结构前三阶固有频率随厚度的增加而增加。结果表明,随着厚度h 的增加,波纹曲梁结构固有频率向高频方向移动,波纹曲梁结构稳定性得到显著提高。
紧接着研究曲率半径R 对波纹曲梁结构固有频率的影响,具体结果如图4 所示。除了曲率半径R 以外,其余模型参数均与表2 中所用的模型参数相同。

图4 波纹曲梁结构固有频率随曲率半径的变化规律
从图4 不难看出,在简支边界条件下,波纹曲梁结构前三阶固有频率随曲率半径R 的增加而减小。结果表明,随着曲率半径R 的增加,波纹曲梁结构固有频率向低频方向移动,波纹曲梁结构稳定性显著降低。
最后研究曲梁弧度α 对波纹曲梁结构前三阶固有频率的影响,具体结果如图5 所示。除了曲梁弧度α 以外,其余模型参数与表2 中所用的模型参数相同。
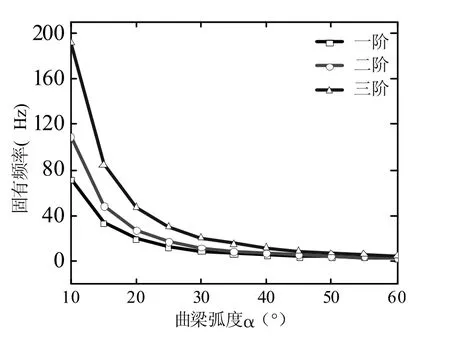
图5 波纹曲梁结构固有频率随曲梁弧度的变化规律
从图5 可以看出,前三阶固有频率随着曲梁弧度的增加而减少。结果表明,随着曲梁弧度α 的增加,波纹曲梁结构固有频率向低频方向移动,波纹曲梁结构稳定性显著降低。
3 结论
3.1 本文基于厚曲梁理论,采用有限元法建立一般边界条件下波纹曲梁结构统一动力学分析模型。
3.2 将本文模型求解结果与有限元软件计算结果进行对比,开展模型验证。结果表明,本文模型求解具有较好稳定性和求解精度,可以用于求解一般边界条件下波纹曲梁结构的自由振动特性。
3.3 对已建立波纹曲梁结构开展参数化研究,结果表明随着厚度增加,波纹曲梁结构共振频率向高频方向移动,稳定性得到显著提高。随着曲率半径和曲梁弧度的增加,波纹结构固有频率向低频移动,稳定性得到显著降低。

