基于电波折射的实时数字引导修正方法

顾保国 郝耀峰 肖艳青 王国林 毛 磊

(中国人民解放军 63726 部队,宁夏 银川 750004)

在航天测控设备捕获跟踪目标的过程中, 中心计算机需要实时向测控设备发送数字引导信息,使测控设备能够及时捕获目标并稳定跟踪目标[1],特别是在初始捕获阶段和丢失目标后的重捕阶段[2],实时数字引导是重要辅助捕获手段。数字引导利用已跟踪目标的测控设备的测量数据或理论弹道, 经过实时数据处理后, 向被引导的测控设备提供实时数字引导信息, 控制天线指向目标将进入的某一空域[3]。由于大气层空气分布不均匀,因此无线电波在大气层中传播有折射现象[4],其传播路径是曲线,而不是直线[5]。随着计算机技术和实时数据处理技术的发展,实时数字引导的精度也越来越高,对于宽波束天线而言,可以利用实时数字引导直接捕获目标,无需考虑电波折射的影响；但对于窄波束天线而言,由于在初始捕获阶段俯仰角度较低,电波折射比较严重,目标的真实位置与视在位置偏差较大[6],研究结果表明[7],在仰角低于6°时,俯仰角偏差超过了0.1°,甚至超过了天线的半波束宽度,在低仰角直接采用数字引导几乎无法捕获目标。

在航天测控中,目前关于电波折射修正的应用,主要是在事后测量数据的误差修正中,文献[8]以测站历史气象数据建立折射率剖面统计模型,并对常用的折射修正模型进行了仿真分析；文献[9]给出了对流层和电离层折射参数实时高精度遥感和探测方法,以实现S 波段雷达折射误差修正；文献[10]提出了一种基于傅立叶残差修正而不需要气象参数的修正方法。这些文献中所采用的修正模型都涉及复杂的微积分运算,虽然精度很高,但是迭代次数多、计算量大,需要消耗大量的计算资源,有的还甚至需要高空气象数据的支持,而地面测控设备一般只配备地面气象仪、测控设备计算机运算能力有限,上述算法限制了其在实时数引修正中使用。

针对实时数引修正的现实需要和现实条件,本文提出了一种基于实时气象数据的电波折射修正方法,利用大气参数计算大气折射率,进而利用大气折射率计算出电波折射误差,然后用这个误差来修正中心的实时数引。文末利用实测数据进行实验验证,实验结果表明,该方法能够将天线准确引导至目标的视在位置,大大提高了目标的捕获跟踪概率。

1 电波折射模型

1.1 模型选取原则

在实时数字引导中引入电波折射修正,是为了把天线的指向位置由实际位置修正到视在位置,并且这种修正主要是在低仰角时使用(俯仰角低于10°),高仰角时由于电波折射相对于天线波束来说已经很小了,加之有实时性的要求,因此相对于事后数据处理来说,在实时数引中使用的电波折射模型要求运算速度快、资源消耗少、精度要求稍低。因此在模型选取上,要选取没有微积分运算、没有迭代运算等形式简单而又具有一定精度的模型。

1.2 模型选取

一般情况下,大气折射率在垂直方向上的变化远远大于其在水平方向上的变化,相差1～3 个数量级[11],因此可以不用考虑电波在方位上的折射误差,只需考虑其在俯仰上的折射误差[12],下文所述的折射误差均指的是在俯仰角上的误差。

根据大气物理学相关知识,在一定的频率范围内,大气折射率是气温、气压和大气湿度等大气参数的函数[13-14],由于大气参数分布无法精确描述,从而也无法精确描述电波在大气层内的精确轨迹[15]。

在大气层内传统的电波折射修正模型有线性模型、指数模型、双指数模型、Hopfield 模型和分段模型等。线性模型公式计算简单,在近地面的高度跟实际观测结果比较接近,通常在1km 以下高度可以使用线性模型[16],但是超出这个高度会有较大的误差[17]; 相关统计结果表明,在海拔高度大于1km 范围内,平均大气折射率用指数模型近似精度较高[17],但计算精度取决于大气分层,大气分层越多,计算量越大,精度越高; Hopfield 模型是根据大气中的温度随高度的变化的统计学模型和大气静力学方程而建立起来的模型[18]。在地面1km 以内,线性模型符合较好,超过1km 时,在1～9km 和9～60km 两个不同的高度范围内呈不同的指数衰减,因此采用分段的方法更能精确描述大气折射率。

实际上,测控设备所跟踪的目标,其高度和距离从几公里到几千公里不等,空间跨度很大,而上述模型要么只适用于低空目标,要么耗费较高的运算资源,若应用在实时处理中,其费效比较高,显然不适用。利用经验模型,可以兼顾计算精度和计算复杂度两个方面的要求,文献[19]给出了电波折射误差△E 的计算公式：

式中,r0为地球平均半径(取6370m),RC为目标与测控设备的测量斜距(即视在斜距,单位：m)。

在海平面,N 的典型值为313,当海拔高度分别为1000m 和2000m 时,N 的典型值相应的为271 和234,这里 分别选,313、271 和234 三个典型值,俯仰角度E 分别选取0.5°、1°、1.5°、2°、3°、5°六个典型值,在目标斜距分别为500km 和800km 时的电波折射误差,依据模型计算结果如表1 和表2 所示。

表1 目标斜距为500km 时的电波折射误差

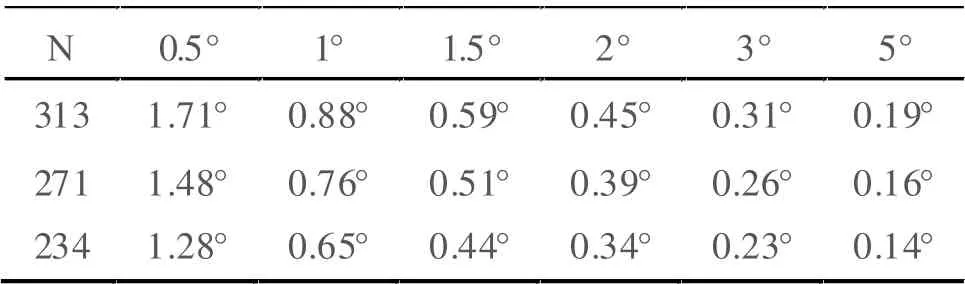
表2 目标斜距为800km 时的电波折射误差

从表1、表2 可以看出,目标距离越远、仰角越低、测站海拔越低,电波折射误差越大。对于半波束宽度小于0.1°的窄波束天线而言,如果不进行电波折射修正,在低海拔地区跟踪500km 以上的目标时,跟踪仰角必须大于5°才有可能利用实时数引直接捕获目标。

1.3 模型使用

测控设备配备的地面气象仪可以实时获取地面温度、湿度和气压等气象数据,根据气象仪的测量数据,利用式(4)、(3)可以计算出测控设备所在位置的地面大气折射率N0。

这里的气象数据利用自动气象仪向测控设备发送的实时测量数据；由于测控设备跟踪目标的时间一般在1小时以内,在此如此小的时间跨度内,地面的温度、湿度和气压的变化很小,因此,也可以用目标飞行开始前气象仪测得的气象数据(即准实时气象数据),作为大气折射率的计算依据；如果测控设备未配备地面气象仪,则可以用手机(网络)查询所在区域的气象数据,由此计算的大气折射率与基于实时数据所计算的大气折射率偏差在15%左右[20]。

2 数引修正及实验验证

2.1 修正方法

2.2 实验验证

为了验证本文的方法的有效性,采用如下流程进行：

Step1：准备某次任务的实时数引数据、测控设备(记为“测站1”)的自跟踪测量数据和事后精确数据；

Step2：比较实时数引数据和事后精确数据的偏差；

Step3：比较实时数引数据加入电波折射修正和不加入电波折射修正两种情况下与自跟踪测量数据的偏差；

Step4：选取同一次任务的另外一套测控设备(记为“测站2”),重复Step1～Step3。

测站1 和测站2 的实时数引数据与事后精确数据的偏差曲线分别如图1、图2 所示。测站1 实时数引数据加入/不加入电波折射修正与自跟踪测量数据的偏差如图3 所示。测站2 实时数引数据加入/不加入电波折射修正与自跟踪测量数据的偏差如图4 所示。测站1 和测站2的数引俯仰角在不同角度下的电波折射修正量本文的方法与Hopfield 模型的对比如表3、表4 所示。

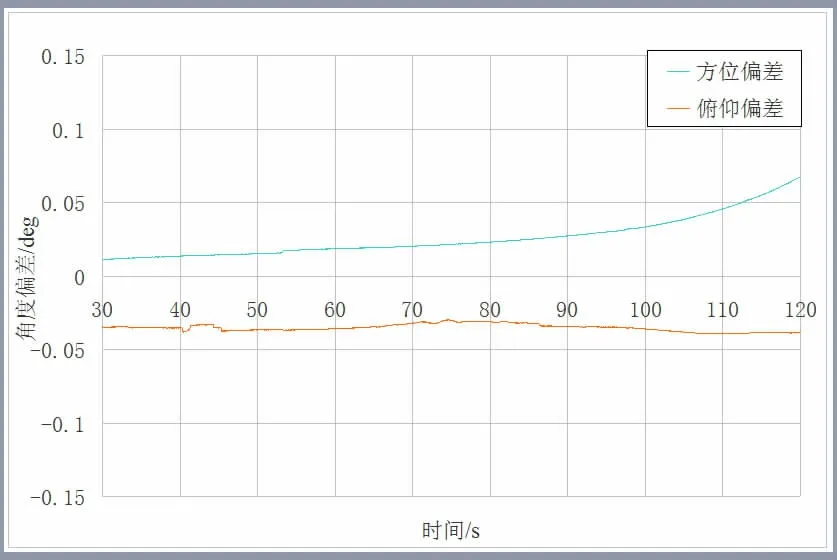
图1 测站1 实时数引与事后精确数据的偏差

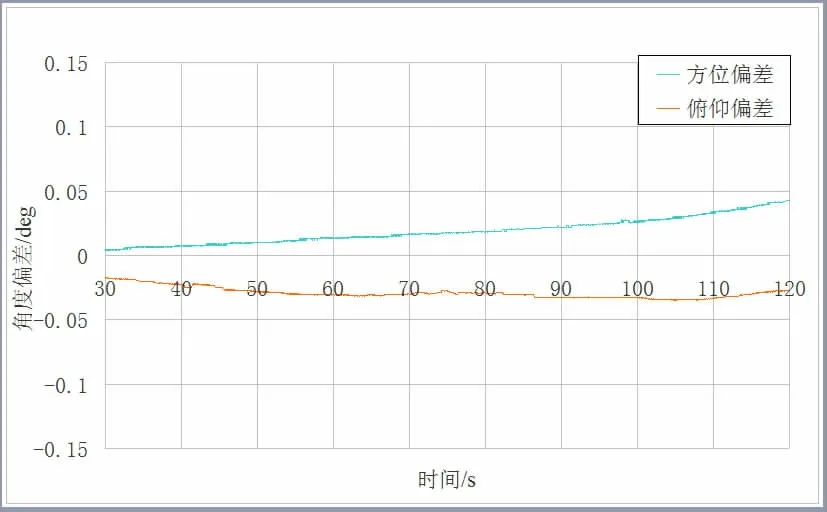
图2 测站2 实时数引与事后精确数据的偏差

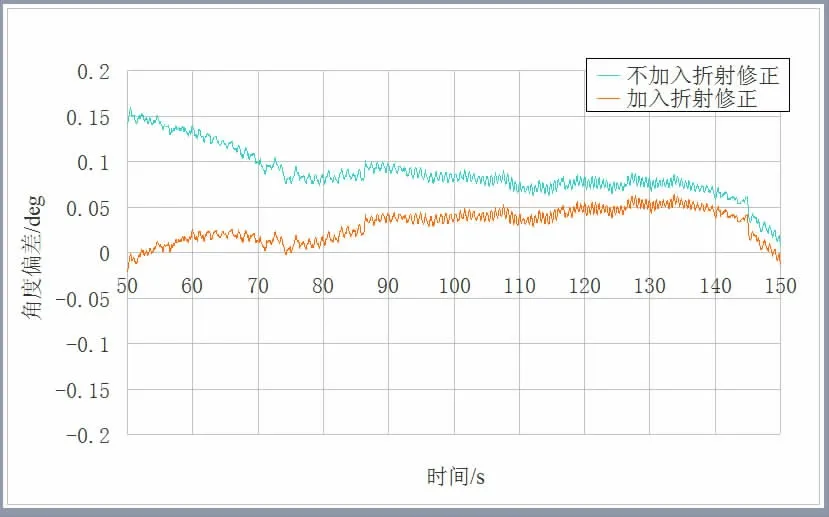
图3 测站1 实时数引数据加入/不加入电波折射修正与自跟踪测量数据的偏差

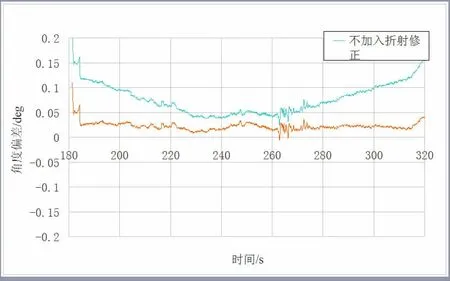
图4 测站2 实时数引数据加入/不加入电波折射修正与自跟踪测量数据的偏差

表3 不同测站在不同数引俯仰角下的电波折射修正量

表4 本文算法计算的电波折射角度与精确模型计算的折射修正量偏差

通过上述实验,结果表明：

(1)实时数引数据在绝大部分时间段落内,与目标真实位置的偏差较小,只有半波束宽度的1/2(以波束宽度为0.2°计),实时数引较为真实的反映了目标的真实位置；

(2)在俯仰角低于6°时,电波折射误差超过了窄波束天线的半波束宽度,无法采用数引直接捕获目标；

(3)本文所采用的电波折射修正方法与精确方法相比,本文的折射修正量偏大,在俯仰角大于0.5 时,两者的偏差小于0.1°,仰角越高,偏差越小。

2.3 仿真分析

以3dB 波束宽度为0.2°(半波束宽度为0.1°)的窄波束天线为例,仿真分析目标偏离天线中心不同角度下的捕获概率,仿真结果如图5 所示。

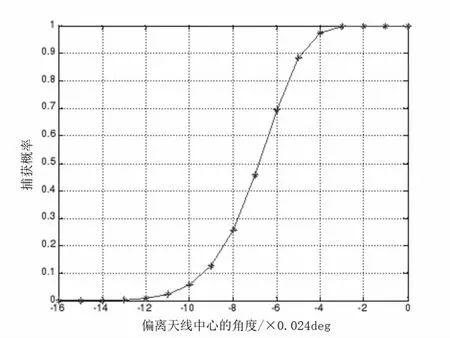
图5 目标偏离天线中心不同角度下的捕获概率图

仿真结果表明,当目标与天线中心的偏差小于0.1°时,捕获概率达到0.88 以上；偏差大于0.2°时,捕获概率在0.05 以下。综合图1、图2 的数据,在捕获初始段,数引俯仰角比目标真实位置低0.03°左右,根据精确模型计算的折射率比本文计算的结果小0.08°左右,由此计算,数引进行折射修正后的角度比目标的视在位置大0.05°,捕获概率为0.99；若不对数引进行修正,在俯仰角为0.1°位置的捕获概率为0.25,因此,采用本文的方法,俯仰角为0.1°时可将捕获概率由0.25 提高到0.99。

结束语

基于实时的气象数据,计算地面大气折射率,通过模型计算电波折射误差,然后用此误差来修正实时数引,通过此方法,对于半波束宽度为0.1°的窄波束天线,可以将数引直接捕获目标(在视距500km 条件下)的角度下限由原来的5°降低到0.1°,不仅大大提高了数引直接捕获目标的概率,而且延长了跟踪目标的有效时间。目前该方法已经在某型窄波束测控设备上得到应用,后续将推广到其它窄波束测控设备中。下一步,还将开展光学测控设备大气折射修正,进一步提高光学测控设备的捕获跟踪能力。