变曲率均质梁结构的振动特性研究
于春蕾, 冀浩杰, 孟忠良,3, 卢纪丽, 徐 伟, C.Chiu
(1.枣庄学院 机电工程学院,山东 枣庄 277160;2.北京航空航天大学 电子信息工程学院, 北京 100191; 3.山东大学 海洋研究院,山东 青岛 266237)
曲梁结构的结构形式多种多样,常见的结构主要包括圆弧曲梁、椭圆曲梁、抛物曲梁和双曲曲梁等。曲梁结构以其形状易改变、力学性能优良、承载能力强等一系列优点,在复杂管路建模方面能够很好的对弯曲管路进行曲梁结构等效并进行动态分析,例如:对航空器中的输油管路、液压管路[1]等。此外,曲梁结构还广泛地应用于建筑、桥梁、机械、船舶等领域。其中,曲梁结构的振动行为不仅影响自身承载能力和稳定性,同时其直接影响与其相连结构的动力学特性。因此,开展曲梁结构的振动特性研究,为其结构设计和优化提供理论基础和技术支持具有十分重要的意义。
叶康生等[2-3]基于p型超收敛算法研究了Timoshenko曲梁和Euler曲梁结构的自由振动特性。武兰河等[4-5]采用微分容积法和空间迭代法研究了圆弧梁面内的振动特性。叶康生等[6]采用动力刚度法研究了平面曲梁的面外自由振动特性。许杠[7]基于求积元法推导了曲梁结构的刚度矩阵,研究了曲梁结构的非线性动力学特性。赵翔等[8]运用格林函数建立Timoshenko曲梁的振动方程并对其进行了强迫振动分析。孙广俊等[9]采用微分求积法研究了单跨圆形、回旋缓和曲线梁的固有振动特性,同时研究了边界条件、刚度比和翘曲系数对其振动频率的影响。陈明飞等[10]基于一阶剪切变形理论和等几何有限元法建立了任意曲率功能梯度曲梁的分析模型,并对其自由振动特性开展了参数化研究。张建书等[11]基于浮动框架有限元法和哈密尔顿原理建立了空间大运动曲梁的动力学模型,研究了应力刚化效应对其动力学特性的影响规律。
Corrêa等[12]采用广义有限元法研究了薄壁和厚壁弯曲梁模型的自由振动特性。Jockovic等[13]采用等几何法研究了伯努利-欧拉曲线梁和瑞利曲线梁的自由振动特性。Luu等[14]基于剪切变形理论建立了椭圆曲梁等的几何模型,同时研究了几何参数对其非线性屈曲和后屈曲行为的影响。Lee等[15-16]基于Timoshenko梁理论,采用龙格库塔法和行列式搜索等方法研究了弹性地基下非规则曲梁(椭圆、正弦和抛物曲梁)的弯曲和扭转振动特性。Chen等[17]采用等几何法建立了功能梯度压电弯曲梁的动力学模型,同时就其结构参数对功能梯度压电弯曲梁的振动特性和瞬态响应的影响进行了研究。Beg等[18]基于有效分层理论,采用哈密尔顿方法系统地研究了功能梯度深曲梁的动力学特性。Ye等[19]提出了一种精确的光谱采样表面方法,研究了变曲率弯曲梁结构的振动特性。考虑剪切变形和转动惯量的影响,Tseng等[20]基于Timoshenko曲梁理论研究了变曲率复合材料层合梁的自由振动特性。
此外,在工程应用中结构经常处于弹性支撑或半刚性连接(螺栓连接)中。当结构处于复杂工作环境下,边界条件可能会产生变化,例如:螺栓连接中螺栓的松动。因此,弹性边界引起了研究人员广泛的关注。Ye等[21]基于广义哈密尔顿原理和谐波平衡法研究了曲梁在非线性边界下的非线性振动特性。Su等[22]采用改进变分法建立了弹性边界条件下功能梯度多孔压电曲梁的动力学模型,研究了其振动特性。Sun等[23]提出弹性边界下具有大曲率梁的数学模型,并研究了其涡激振动和涡激发散响应。
综上所述,现有研究多采用等几何法和有限元等方法对曲梁结构的振动特性进行分析且其所建模型存在只能求解特定结构的曲梁结构等局限性。鉴于现有研究的不足,本文基于一阶剪切变形理论和哈密尔顿原理建立了复杂边界条件下四种典型曲梁结构的统一动力学分析模型,研究了复杂边界条件下任意变曲率曲梁结构的自由振动特性和受迫响应。本文建立的曲梁结构模型具有收敛性好、计算效率高和计算精度高等优点。本文研究内容主要包括三部分:首先,建立四种典型曲梁结构的统一动力学分析模型并验证模型的收敛性。然后,与现有文献结果和有限元软件ABAQUS仿真结果进行对比分析,验证所建模型的准确性。最后,开展曲梁结构参数、边界条件以及脉冲载荷类型对其稳态和瞬态响应的影响研究,为曲梁结构的结构设计和优化提供理论和技术支持。
1 理论推导
1.1 曲梁结构模型介绍
曲梁结构及其边界条件示意图,如图1所示。选取正交坐标系对曲梁结构进行描述,考虑3个方向的自由度x,y,z。u,v,w分别表示对应于x,y,z3个方向上的位移分量。曲梁的中性面被视作参考平面,其中心线表示曲梁的中心线。为便于描述中心线的变化规律,选用φ代替x进行描述。h和b分别表示曲梁的厚度和宽度。Rφ表示曲率半径,当Rφ=∞时,曲梁可以被视作直梁。此外,如图1所示本文曲梁结构的约束条件采用边界弹簧进行施加,ku,kw,kφ分别表示边界弹簧的3个方向的弹簧刚度。
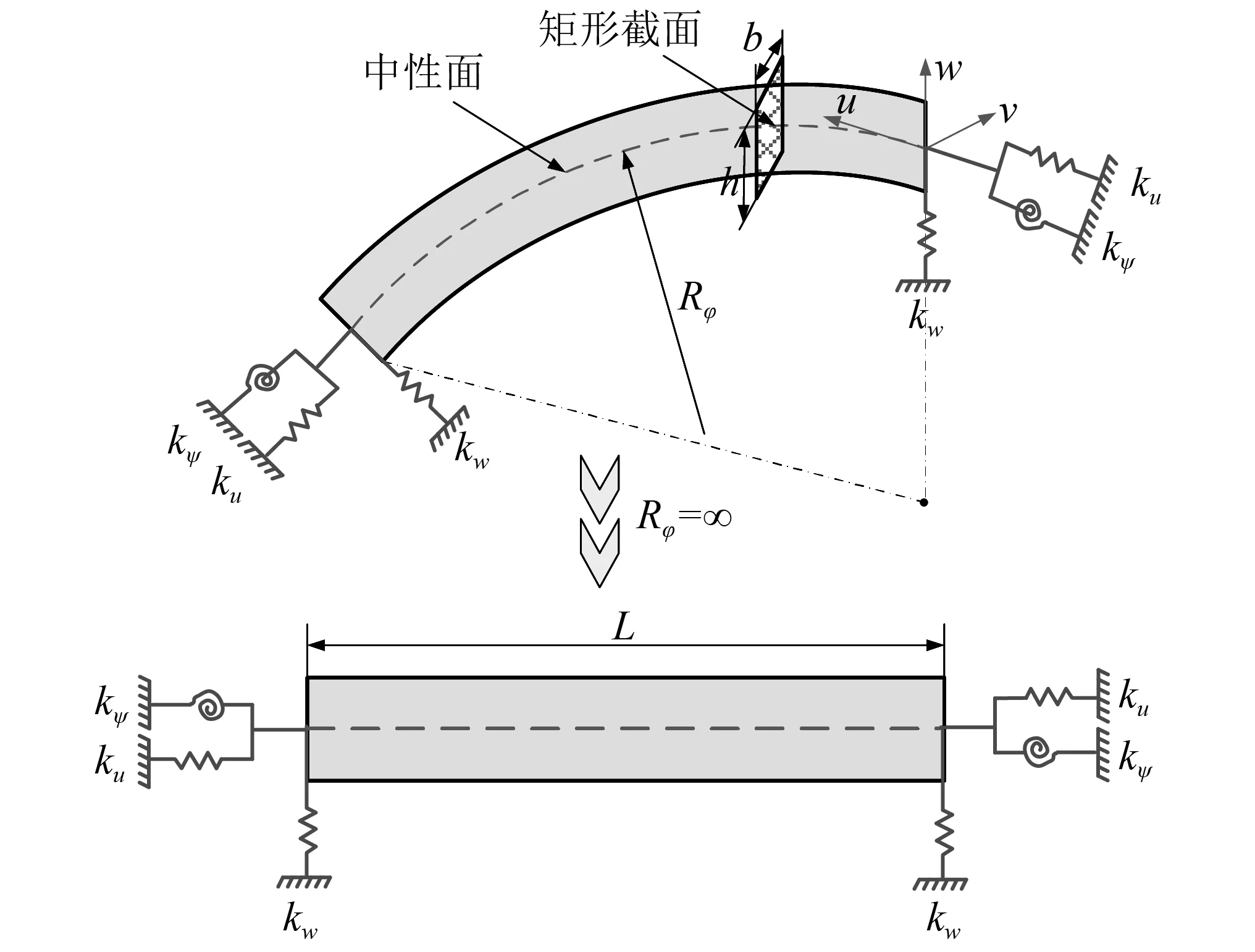
图1 曲梁结构及边界条件示意图Fig.1 Schematic diagram of curved beam structure and boundary condition
为了方便起见,本文假定曲梁均是以中心线为变化特征,仅考虑xz平面内的变形。同时指出,本文主要研究对象包括圆弧、椭圆、抛物和双曲曲梁四种典型的曲梁结构,其具体结构如图2所示。
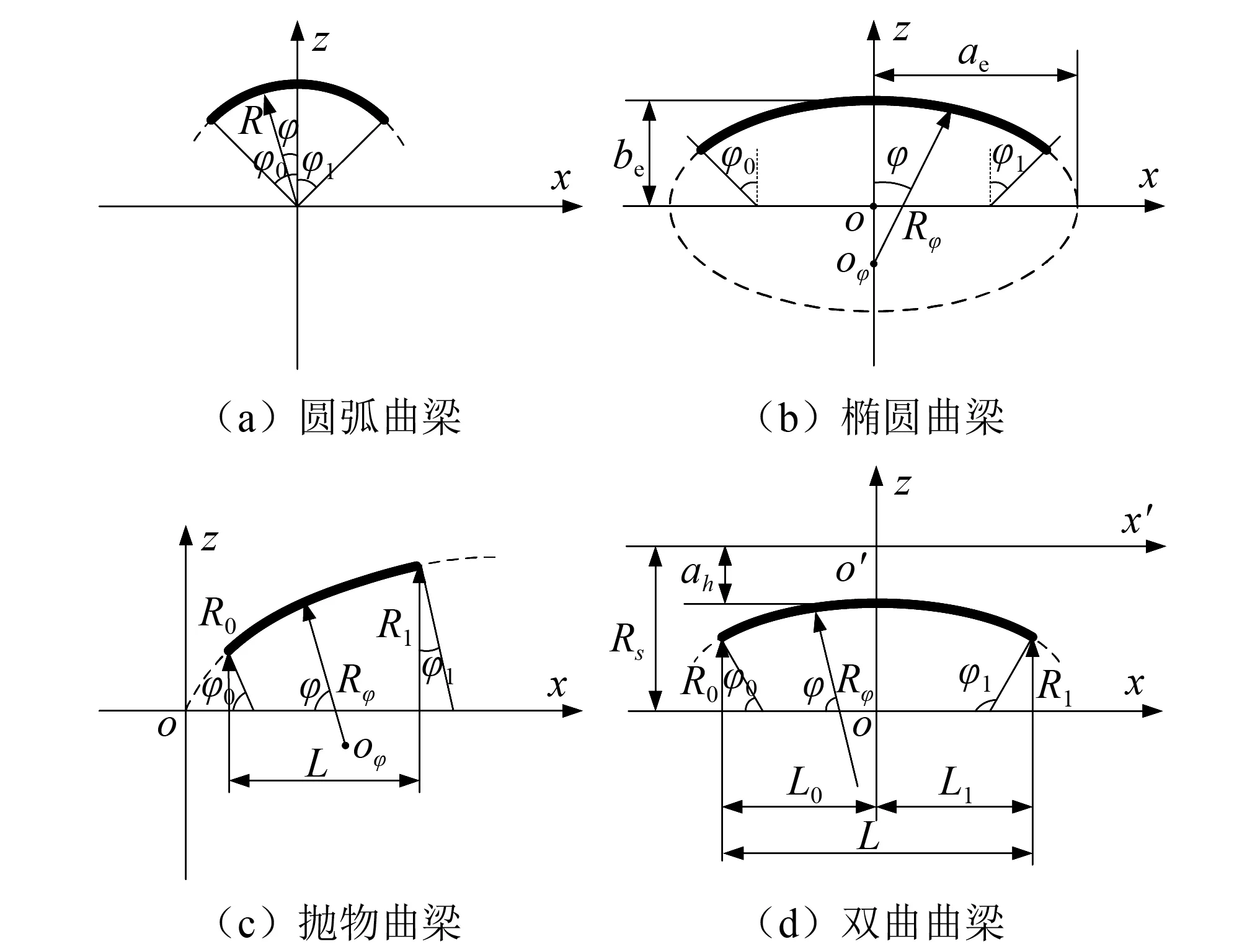
图2 四种典型曲梁结构示意图Fig.2 Schematic diagram of four typical curved beam structures
圆弧曲梁的结构示意图见图2(a)。图2(a)中:φ0和φ1分别为圆弧曲梁的起始和终止角度;R(φ)为曲率半径,对于圆弧曲梁来说,曲率半径是一个定值,即R(φ)=R。
椭圆曲梁的结构示意图见图2(b)。图2(b)中:φ0和φ1分别为椭圆曲梁的起始和终止角度;ae和be分别为椭圆的长半轴和短半轴的长度;R(φ)为曲率半径,其具体表达式如式(1)所示
(1)
抛物曲梁的结构示意图见图2(c)。图2(c)中:φ0和φ1分别为抛物曲梁的起始和终止角度,其表达式如下所示;L为抛物曲梁沿x轴方向的长度;R0和R1分别为抛物曲梁起始和终止点的半径;R(φ) 为曲率半径,其具体表达式如式(2)所示
(2)
式中,k为抛物线曲率的特征参数。
双曲曲梁的结构示意图见图2(d)。图2(d)中:φ0和φ1分别为双曲曲梁的起始和终止角度,其表达式如下所示;R0和R1分别为双曲曲梁起始和终止点的半径;L0和L1分别为双曲曲梁起始和终止点到坐标原点的距离;L为双曲曲梁沿x轴方向的长度;Rs为旋转轴x′到几何轴x之间的垂直距离;ah为双曲线半横轴的长度;Rs为双曲曲梁的曲率半径,其具体表达式如式(3)所示
(3)
式中,bh为双曲线共轭半轴的长度。
1.2 曲梁结构模型建立
根据一阶剪切变形梁理论,曲梁上任意一点的位移函数可以写成
U(φ,y,z,t)=u(φ,y,t)+zψφ(φ,y,t),
W(φ,y,z,t)=w(φ,y,t)
(4)
式中:U和W分别为曲梁上任意一点沿φ和z方向的位移分量;u和w分别为曲梁中性面上相应点的位移分量;ψφ为φ轴法线方向绕曲梁中性面的旋转分量。
根据曲梁结构应变与位移之间的线性关系,曲梁结构的应变可以写成
(5)
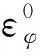
(6)
根据一阶剪切变形梁理论,曲梁的本构方程可以写成
σ=Aε,
(7a)
(7b)
式中:σ为应力向量;N为由面内应力、弯曲和扭转组成的应力向量;Nφ,Ny和Nφy为面内应力;My为弯矩;Mφy为扭矩;ε为由中性面上应变和曲率组成应变向量;κ为剪切变形因子,一般取值为5/6;A为应变与应力之间的变换矩阵,A矩阵中Aij,Bij和Cij(i,j=1, 2, 6)的具体表达式为
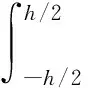
(8a)
(8b)
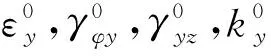
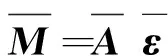
(9a)
(9b)
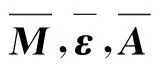
根据能量原理,曲梁结构的应变能可以定义为
(10)
同理,曲梁结构的动能可以定义为
(11)
式中:“·”为对时间t求一阶导数;ρ为曲梁结构的密度。同时指出,在研究曲梁结构的受迫振动时,应该考虑由外载荷引起的势能,其具体表达式为
(12)
式中,fu,fw和ψφ分别为外载荷力和力矩。由上所述,本文选用边界弹簧来模拟曲梁结构的边界条件,所以必须考虑边界弹簧的势能,具体表达式为
(13)
式中:kLu,kLw和kLφ为曲梁结构左侧边界弹簧的弹簧刚度;kRu,kRw和kRφ为曲梁结构右侧边界弹簧的弹簧刚度。
综上所述,本节已经给出了曲梁结构的应变能、动能、外力势能和边界弹簧势能的表达式。根据哈密尔顿原理,拉格朗日函数Π的表达式为
Π=U-T+W+Ub
(14)
1.3 曲梁结构模型求解
为了便于对上述模型进行求解,提高收敛速度,本文选取切比雪夫多项式和傅里叶级数来描述曲梁结构的位移容许函数,其具体表达式为
(15)
式中:u为曲梁位移分量组成的列向量;Um为与位移分量相对应的假定位移系数组成的列向量;ω为角频率;t为时间变量;M为位移容许函数的最高阶次(截断数);Pm(φ) 为关于位移分量的第m阶切比雪夫多项式,其具体表达式为
P0(φ)=1,P1(φ)=φ
(16a)
Pt(φ)=2φPt(φ)-Pt-1(φ),2≤t≤M
(16b)
通过使用Ritz方法,可以得到
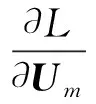
(17)
进而得到了曲梁结构的质量矩阵和刚度矩阵
(18a)
(18b)
通过添加外部载荷后可以得到曲梁结构的特征方程,具体表达式为
(19)
式中:q为广义位移列向量;M和K分别为曲梁结构的质量矩阵和刚度矩阵;Kb为由边界弹簧引起的刚度矩阵;F为外载荷矩阵。假定曲梁做谐波运动,在不考虑外载荷的情况下,曲梁的特征方程将变换成
(20a)
(20b)
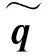
通过式(19)和式(20)可以求解曲梁结构的自由振动和受迫响应(稳态响应和瞬态响应)。为了便于直观描述本文模型的求解过程,本节给出了曲梁结构振动特性求解的流程图,如图3所示。
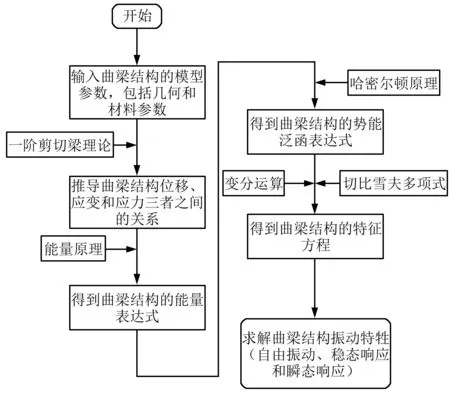
图3 模型求解流程图Fig.3 Flow chart of model solving
2 算例分析
2.1 模型收敛性验证
曲梁结构的收敛性验证主要包括2个方面:一方面是关于截断数的收敛性验证;另一方面是关于边界弹簧刚度的收敛性验证。前者是为了确定模型求解的最佳截断数,后者是为了确定模型求解的最佳边界弹簧刚度,具体求解结果如图4和图5所示。本文所用曲梁结构的几何参数为:圆弧曲梁——B=h=0.1 m,L=1 m,φ0=-π/3,φ1=π/3,R=L/(φ1-φ2);椭圆曲梁——B=h=0.1 m,ae=1 m,be=0.5 m,φ0=-π/2,φ1=π/2;抛物曲梁——B=h=0.06 m,R0=1 m,R1=2 m,L=1.5 m;双曲曲梁——R0=R1=0.5 m,Rs=4 m,ah=3 m,L0=1 m,L1=1 m,L=2 m,B=h=L/25。曲梁结构的材料参数为:E=70 GPa,ρ=2 702 kg/m3,v=0.3。曲梁结构的边界条件为自由边界。
从图4可以看出,四种典型曲梁结构的一阶无量纲频率随着截断数的增加均趋向于某一定值。上述模型结果趋于定值现象说明模型结果已经收敛。为了保证模型收敛的速度和求解精度,本文选取模型截断数M为8。同时指出,无量纲频率Ω的表达式为
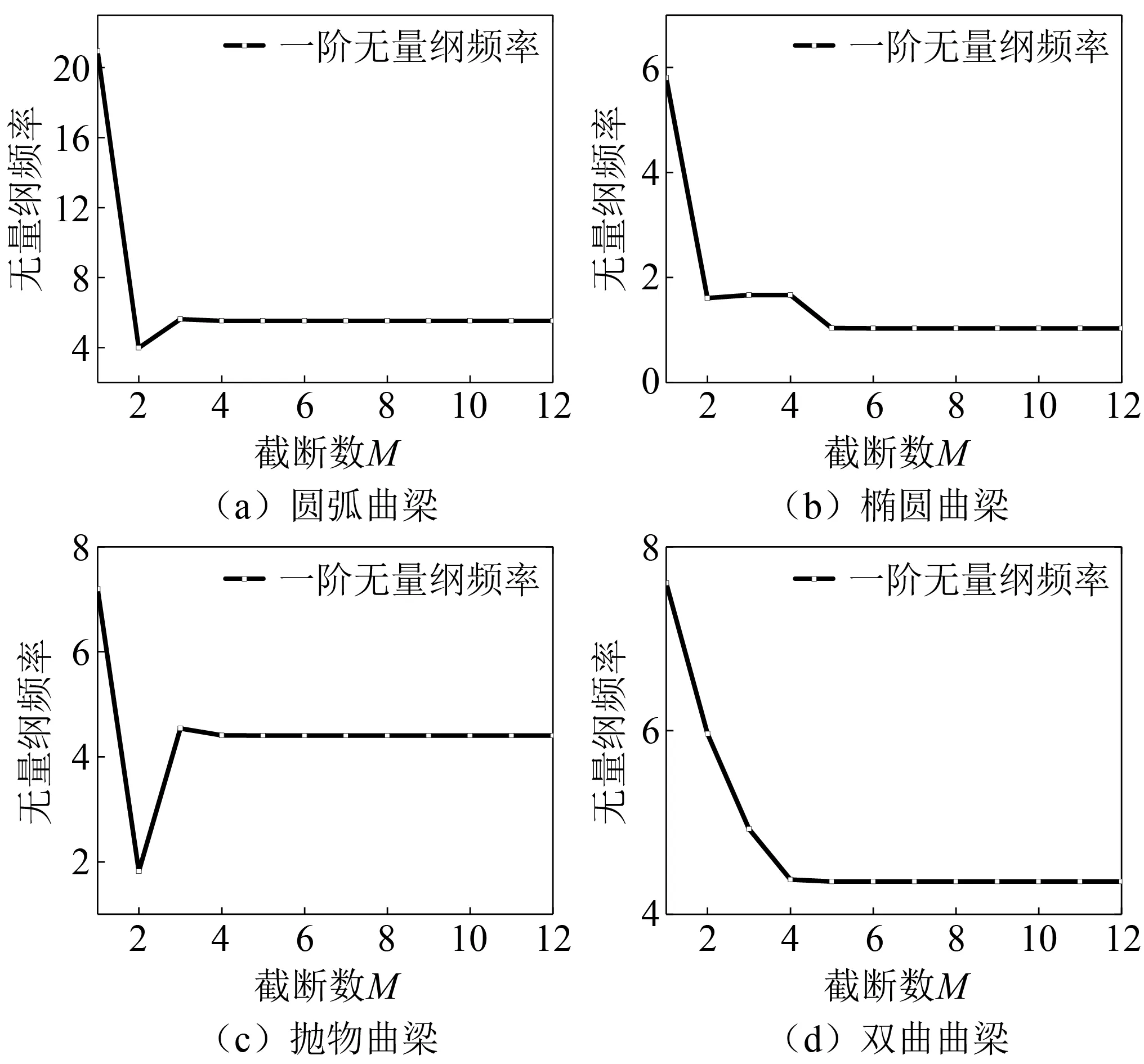
图4 曲梁结构的无量纲频率随截断数的变化规律Fig.4 Variation of dimensionless frequency of curved beam structure with truncation number
(21)
式中:f为曲梁结构的频率;L为曲梁的长度,对于椭圆曲梁来说,其长度为ae。
从图5可以看出,曲梁结构的一阶无量纲频率随着边界弹簧刚度的增加呈现出先保持不变,紧接着增加,后保持不变的变化趋势。上述现象表明当边界弹簧刚度增加到1014时,模型结果已经收敛。根据上述变化规律,可以确定曲梁结构在施加相应边界条件下的弹簧刚度取值。曲梁结构边界条件的定义如下所示:自由边界F-F(ku=kw=kφ=0);固支边界C-C(ku=kw=kφ=1014);简支边界S-S(kw=1014,ku=kφ=0);弹性边界E1-E1(ku=108,kw=kφ=1014),E2-E2(kw=108,ku=kφ=1014),E3-E3(kφ=108,ku=kw=1014),E4-E4(kw=ku=kφ=108)。
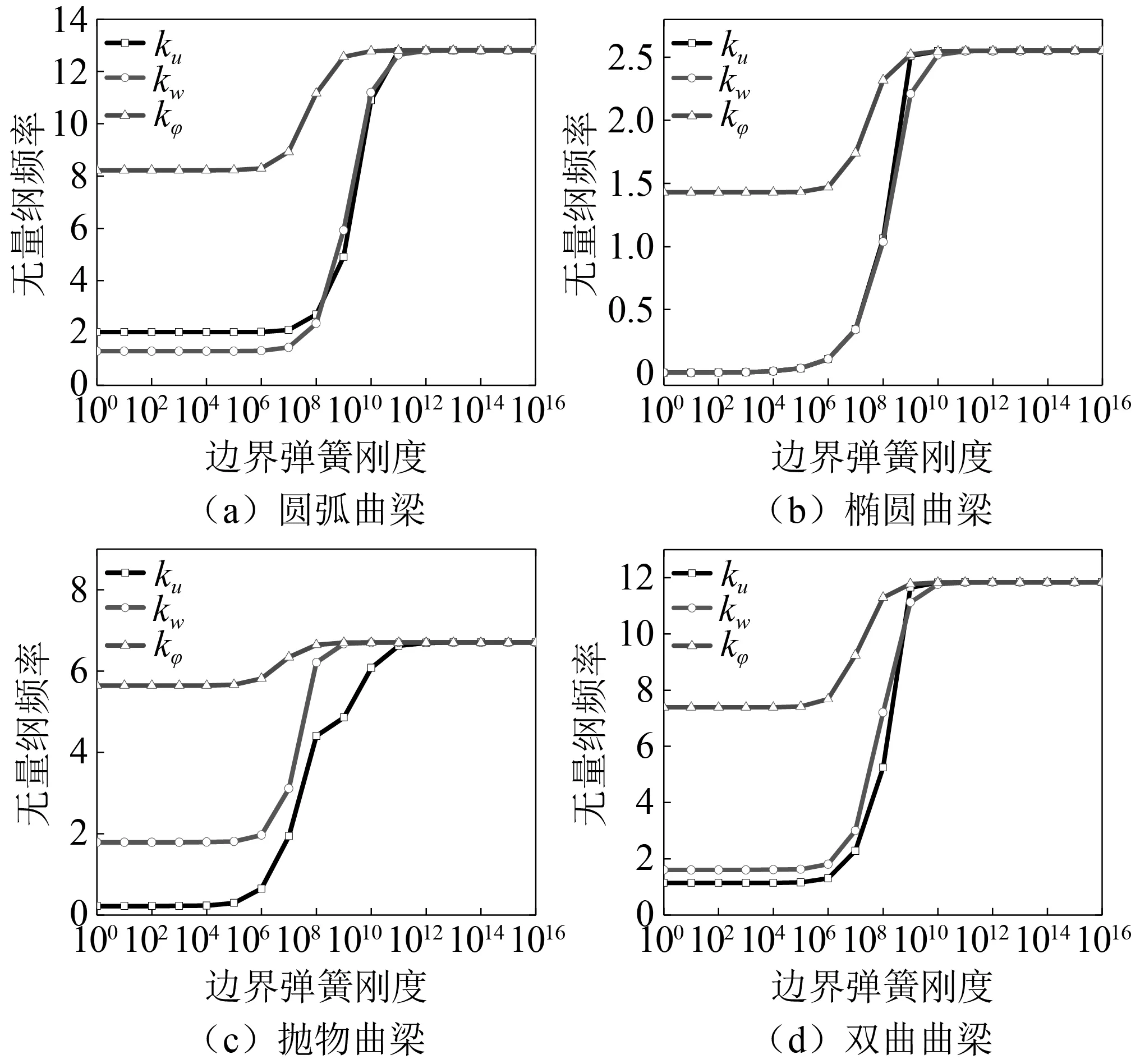
图5 曲梁结构的无量纲频率随边界弹簧刚度的变化规律Fig.5 Variation of dimensionless frequency of curved beam structure with boundary spring stiffness
综上所述,本文所建曲梁结构模型具有良好的收敛性。此外,通过上述分析确定了模型求解过程中截断数和边界弹簧刚度的取值。
2.2 模型准确性验证
基于上述对曲梁结构模型收敛性的验证,本节对其准确性进行验证。模型准确性验证分为固有频率验证、稳态响应验证、瞬态响应验证3个部分。模型准确性验证的具体措施是将本文模型求解结果与现有文献结果和有限元软件ABAQUS分析结果进行对比。模型固有频率的验证结果如表1所示,其曲梁模型的结构参数与图4曲梁结构相同。
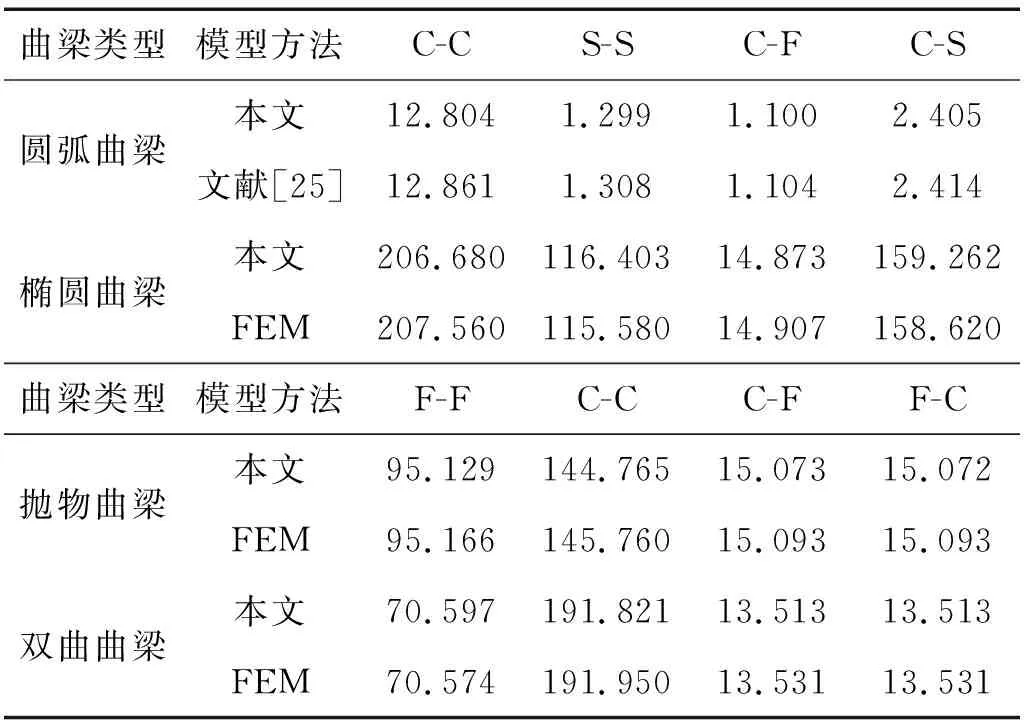
表1 曲梁结构模型的固有频率对比验证Tab.1 Comparison and verification of natural frequencies of curved beam structure model
从表1可以看出,本文模型在不同边界条件下求解得到一阶固有频率与已有文献和有限元软件ABAQUS中相应的计算结果具有较好的一致性,其中有限元方法采用的是ABAQUS中的壳单元,因为壳单元和本文所提出的梁单元都忽略了厚度的影响,所以这两类方法具有很好的一致性。单元数径向划分为85个单元,轴向划分为2个单元,单元总数为85×2。通过对比可以说明本文模型求解曲梁结构自由振动特性的准确性、稳定性和通用性。
曲梁结构模型的稳态响应对比结果,如图6所示。在模型稳态响应验证之前,首先对模型的几何参数、载荷大小以及施加位置进行说明。圆弧曲梁:B=h=0.1 m,L=1 m,φ0=π/6,φ1=5·π/6,R=L/(φ1-φ2);载荷的施加位置[R·cos(π/3), 0.5,R·sin(π/3)];载荷大小(0,0,-1); 测点位置(0,0.5,R);扫频范围200~1 600 Hz。椭圆曲梁:B=h=0.1 m,ae=2 m,be=1 m,φ0=-π/2,φ1=π/2;载荷的施加位置(0,0.5,1);载荷大小(0,0,-1); 测点位置(0,0.5,1);扫频范围200~1 200 Hz。抛物曲梁:B=h=0.1 m,R0=1 m,R1=2 m,L=2 m;载荷的施加位置(1, 0.5, 0.707 1);载荷大小(0.447 ,-0.894 ,0);测点位置(0.5, 0.5, 0.5);扫频范围200~1 000 Hz。双曲曲梁:R0=R1=0.5 m,Rs=4 m,ah=3 m,L0=1 m,L1=1 m,L=2 m,B=h=0.1 m;载荷的施加位置(0, 0.5, 1);载荷大小(0, 0.5, -1);测点位置(0, 0.5, -1);扫频范围200~1 600 Hz。扫频间距均为1 Hz。曲梁模型的材料参数与图4曲梁模型定义相同,曲梁模型边界条件是均为固支边界。
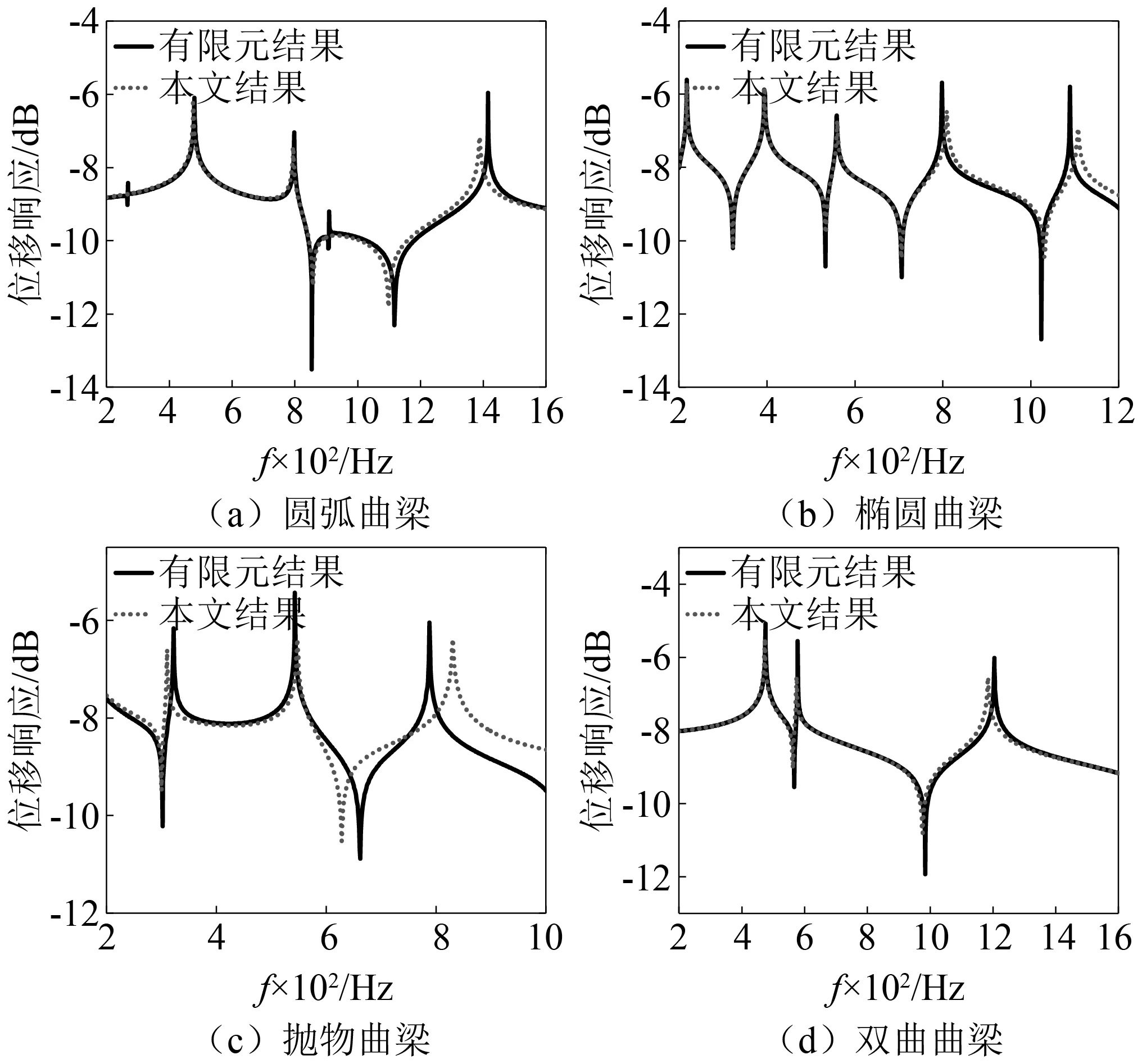
图6 曲梁结构稳态响应的对比结果Fig.6 Comparison results of steady-state response of curved beam structure
从图6可以看出,本文曲梁结构模型求解的稳态响应结果与有限元模型预测结果具有较好的一致性。对于抛物曲梁结构,其在高频段的稳态响应结果与有限元结果存在明显误差,但两者的变化趋势基本一致。分析上述现象,其主要原因为抛物曲梁结构的具有几何不对称的特性,在有限元模拟中可能会因其结构的复杂性产生仿真误差,但误差在可接受的范围内。同时指出,图6中的位移响应是根据实际位移结果换算得到的,具体换算公式为
X=lg[abs(x)]
(22)
式中:x为实际位移响应的计算结果;X为换算后的位移响应结果。
曲梁结构模型的瞬态响应对比结果,如图7所示。曲梁模型的结构参数与图6曲梁模型的参数相同,脉冲载荷的类型为矩形脉冲载荷。对于不同类型的曲梁结构,施加脉冲载荷的时间不同,但其时间步长相同且均为200。
从图7可以看出,本文曲梁结构模型求解的瞬态响应结果与有限元模型的预测结果吻合较好。但对于抛物曲梁,其瞬态响应求解结果与有限元分析结果存在明显误差,产生上述误差的原因与抛物曲梁稳态响应出现的误差原因相同。
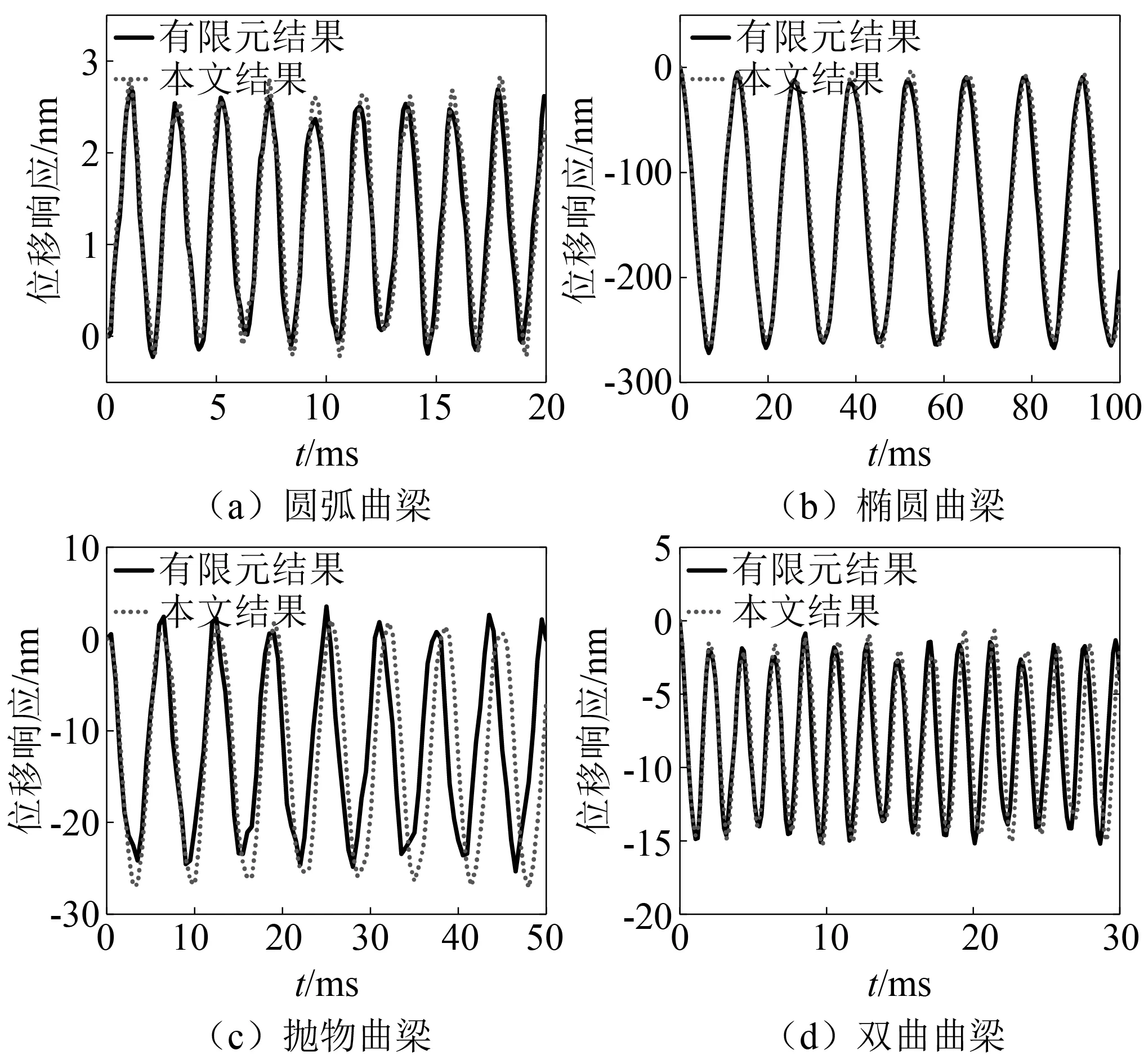
图7 曲梁结构瞬态响应的对比结果Fig.7 Comparison results of transient response of curved beam structure
综上所述,本文所建曲梁结构统一动力学模型可实现对不同类型曲梁结构的振动特性(自由振动、稳态响应和瞬态响应)进行有效预测。
2.3 模型参数化研究
由上所述,本文对已建立的曲梁结构模型进行了收敛性和准确性验证。验证结果表明,本文所建曲梁结构统一动力学分析模型具有较好的收敛性,同时其可实现对复杂边界条件下不同类型曲梁结构模型振动特性的快速高精度求解。基于本文所建曲梁结构模型,本节开展曲梁几何参数、边界条件以及脉冲载荷类型对稳态响应和瞬态响影响的研究,为工程应用中曲梁结构的设计和优化提供理论基础和技术支持。
曲梁结构几何参数对其稳态响应的影响,如图8所示。除了曲梁结构厚度h以外,曲梁结构模型的模型参数与图6所用的模型参数相同。
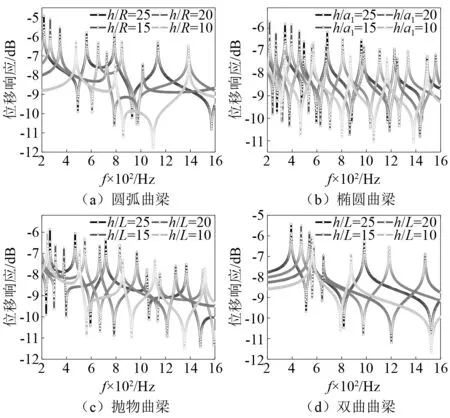
图8 曲梁结构稳态响应随结构厚度的变化规律Fig.8 Variation of steady-state response of curved beam structure with structural thickness
从图8可以看出,曲梁结构位移响应水平的变化规律为:①曲梁结构位移响应水平随着曲梁厚度的增加而明显降低;②曲梁结构位移响应峰值随着曲梁厚度的增加向高频段移动;③曲梁位移响应峰值的数量随着曲梁厚度的增加而减少。分析结果表明,增加曲梁厚度将使曲梁结构的共振频率向高频方向移动,有效提高其稳定性。
曲梁结构边界条件对位移响应的影响结果,如图9所示。本文研究的边界条件是指弹性边界,曲梁结构模型的参数与图7中所用的模型参数相同。
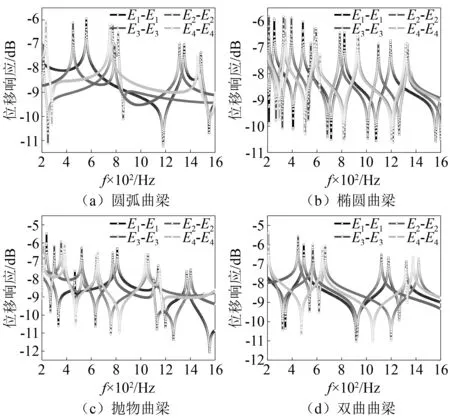
图9 曲梁结构稳态响应随边界条件的变化规律Fig.9 Variation of steady-state response of curved beam structure with boundary conditions
从图9中可以看出,曲梁结构位移响应水平和峰值数量随着弹性边界的变化基本保持不变,但是曲梁结构位移响应峰值会发生移动。此外,随着弹性边界由E1-E1变化E4-E4,曲梁结构位移响应峰值会逐渐向低频方向移动。分析结果表明,曲梁结构在弹性边界E1-E1下的稳定性最好,而在E4-E4边界下稳定性最差。
脉冲载荷类型对曲梁结构瞬态响应的影响结果如图10所示。除了脉冲载荷类型以外,曲梁结构模型的模型参数与图7所用的模型参数相同,脉冲载荷类型的定义见文献[25]。
从图10可以看出,曲梁瞬态响应随脉冲载荷的变化规律为:①在矩形脉冲和指数脉冲载荷下,曲梁结构瞬态响应的变化趋势相同,但两者的瞬态响应峰值有所不同;②在三角形和半正弦脉冲下,曲梁结构瞬态响应的变化趋势基本相同,整体呈正余弦规律变化且位移响应峰值相差不大。分析结果表明,不同的脉冲载荷类型对曲梁结构稳态响应的影响程度的不同,矩形脉冲和三角形脉冲的影响最为显著。
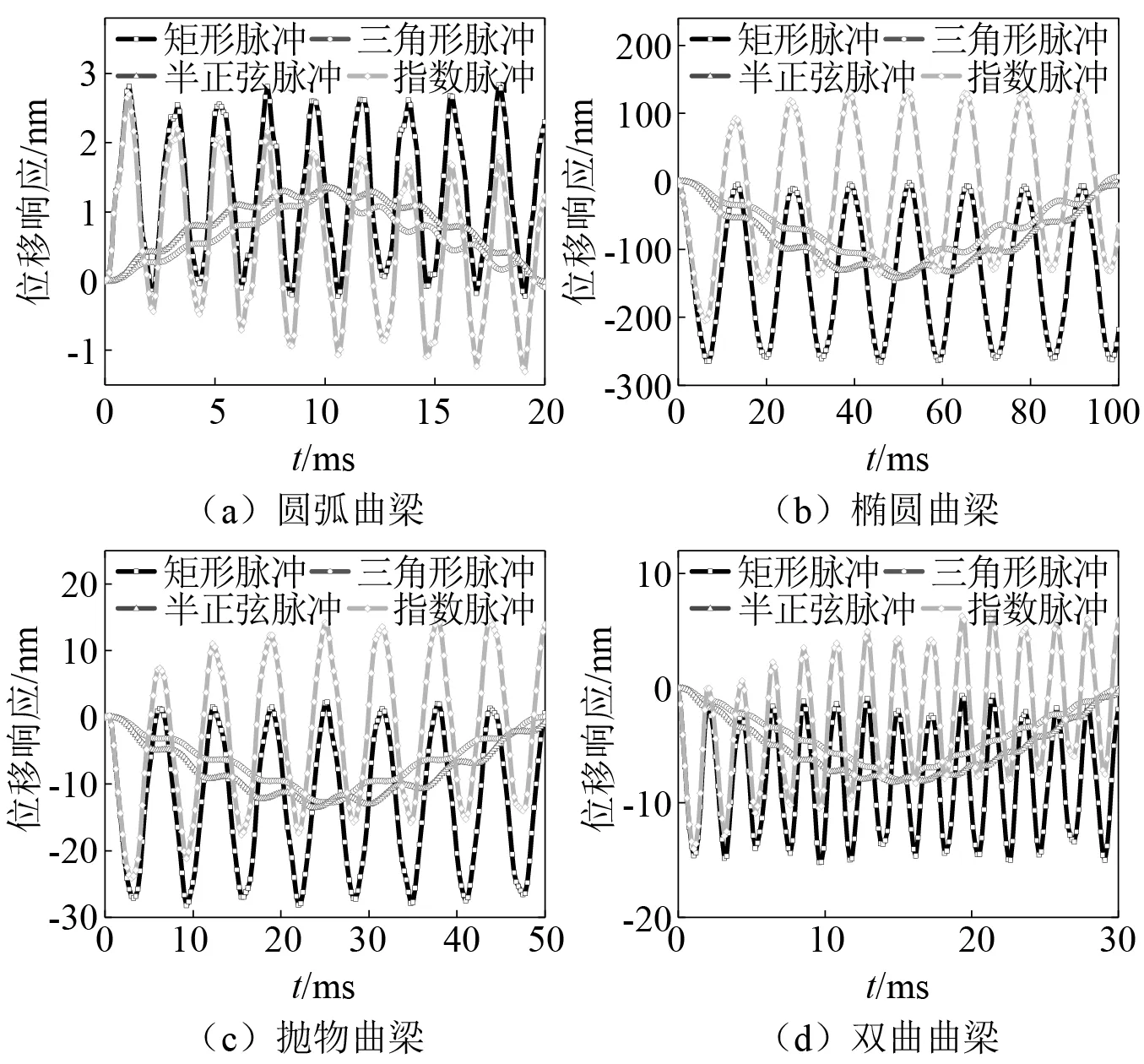
图10 曲梁结构瞬态响应随脉冲载荷的变化规律Fig.10 Variation of transient response of curved beam structure with pulse load
3 结 论
(1) 本文基于一阶剪切变形梁理论和哈密尔顿原理建立了复杂边界条件下曲梁结构的统一动力学分析模型,考虑了4个典型的曲梁结构,即圆弧曲梁、椭圆曲梁、抛物曲梁和双曲曲梁。
(2) 本文建立的曲梁结构统一动力学分析模型具有较好的收敛性和较高的求解精度,可以有效预测复杂边界条件下曲梁结构模型的振动特性,包括自由振动、稳态响应和瞬态响应。
(3) 对曲梁结构模型的结构厚度、弹性边界条件以及脉冲载荷类型开展了参数化研究。分析结果表明,随着曲梁结构厚度的增加其稳定性会提高且共振频率向高频方向移动;随着弹性边界条件的变化,曲梁结构在弹性边界E1-E1下的稳定性最好,在弹性边界E4-E4下的稳定性最差;相较于三角形和半正弦脉冲,矩形脉冲和三角形脉冲载荷对曲梁结构模型的影响显著。

