滚动轴承复合故障的时频能量聚集谱诊断方法

袁 静， 姚 泽， 胡雯玥， 蒋会明， 赵 倩

(上海理工大学 机械工程学院，上海 200093)

旋转机械广泛应用于石油化工、航空航天、轨道交通等行业。滚动轴承作为旋转机械设备传动系统的“关节”，对机械设备工作可靠性与安全性起着关键、重要的作用。由于长期在高速重载、疲劳磨损、高温冲击等恶劣条件下运转，使得滚动轴承极易发生故障[1-3]。一旦滚动轴承发生故障，将直接影响到整个设备的安全性，甚至产生重大的安全事故，造成巨大的经济损失。因此，发展防患于未然的状态检测与故障诊断技术极其重要。然而，由于旋转机械设备运行环境特殊性、内部结构复杂性和运行工况多变性等因素，导致其轴承故障动态信号多呈现出明显的大波动下变转速性、多振动模式混淆性、微弱特征调制性等特点[4-5]。特别是多发或并发的轴承复合故障往往带来强背景噪声干扰下的异样微弱特征提取难题[6]，给旋转机械设备轴承精确诊断带来更大困难。

当滚动轴承发生局部损伤时，损伤点会反复撞击与之接触的其他元件表面而产生非平稳的周期性冲击，而这些周期性的冲击特征被认为是轴承故障的重要标志[7-8]。目前，共振解调技术在滚动轴承诊断中得到普遍认可，其基本原理是根据故障轴承瞬态冲击信息会被调制到高频共振带的特点，通过解调技术实现轴承故障特征提取，其关键在于最优解调频带选取[9-10]。鉴于小波变换具有优良的局部时频特性和滤波特性，被广泛用于共振解调的滤波器[11-13]。Antoni等[14-15]基于短时傅里叶变换和滤波器组提出快速谱峭度算法，提高了计算效率和轴承诊断效果。但存在带宽过大和谱峭度对冲击敏感的不足。文献[16]提出了基于增强熵权峭度图的滚动轴承最优频带解调的故障诊断方法。文献[17]利用经验模式分解对信号进行降噪预处理，再结合谱峭度选取最佳滤波器参数，实现了滚动轴承的早期故障诊断。Dragomiretskiy等[18]提出的变分模态分解广泛应用于轴承故障诊断，但其存在模态分解个数k和约束强度α需要进行预设置且不同参数值对于分解效果影响大的问题。当面对旋转机械轴承复合故障的异样微弱特征提取难题以及不同故障所引发的多个最优解调频带问题，上述方法往往仅能较好地识别复合故障中征兆较明显的单一轴承故障，难以兼顾多个轴承故障特征的同步解调、综合提取与科学正确诊断。

同步压缩变换(synchrosqueezing transform, SST)作为一种强大的时频分析工具，根据瞬时频率估计值在频率方向上对时频能量进行压缩重排，显著提高了能量聚集性，已广泛应用于轴承故障诊断[19-21]。频率划分精细且能量聚集的时频图为复合故障特征的同步解调提取提供了可能。但SST处理冲击信号时仍存在瞬时频率估计误差大的问题，导致在解调频率处能量发散严重，对精准选取最优解调频带产生影响。为此，提出基于多重同步压缩变换的时频能量聚集谱复合轴承故障诊断方法。

多重压缩变换是通过对SST的结果进行多重压缩，进一步提高瞬时频率估计精度，因此时频图能量更加聚集，为精准选取最优解调频带奠定了扎实基础。在时频图中以高能量的形式展示各强弱故障特征的共振频带以及冲击发生的时间。在共振频带上，能量具有周期性，而这种能量周期性就是该故障的故障特征频率，因此只需对各共振频带上的能量进行包络解调即可得到各故障的特征频率。相比于其他方法(找到最优共振解调频带后再构造滤波器对信号进行滤波，最后对滤波后的时域信号进行包络解调)，对共振频带处的能量直接进行包络解调更为简单有效。最优解调频带上的能量最高，其周期性更加明显。为实现同步解调、综合提取、准确输出多个最优解调频带，提出时频能量聚集谱指标即能量聚集谱相对因子。首先对各瞬时频率处的能量进行包络解调，得到能量聚集谱，并求出聚集谱中4种滚动轴承故障特征频率相对因子，筛选出最大因子值。其次，将最大因子对应的频带进行时域重构，并计算峭度值。最后，通过筛选峭度值来准确输出信号中存在的复合故障的最优共振解调频带。采集的振动信号中难免会存在噪声、随机冲击等干扰，但多重压缩变换本身具有一定的抗噪性，而且噪声在时频图中是随机分布的低能量散点，与随机冲击一样没有周期性，因此该指标能减少噪声、随机冲击对选取各故障最优共振解调频带的影响。最后通过轴承试验验证本方法在滚动轴承复合故障诊断中的有效性。

1 同步压缩变换

同步压缩变换是在线性时频变换的基础上通过重排算法对发散的时频能量分布进行压缩，获得高能量聚集的时频表示，同时还保持可逆性。其步骤大致可分为三步。第一步：短时傅里叶变换(short time Fourier transform，STFT)。以多分量非平稳信号f(t)∈L2(R)为例，其信号模型为

(1)

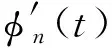
信号f(t)的STFT定义为

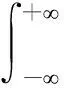
(2)

式中：t为时间变量；η为频率变量；g(t)∈L2(R)为实对称的窗函数。

令gη(τ)=g(τ-t)·ei2πητ，则式(1)可表示为

(3)

(4)

由式(4)可知，信号f(t)经过短时傅里叶变换后，得到的时频能量分布是以频率η=2πω为中心产生能量发散，因此STFT的时频图能量聚集性差。为提高能量聚集性，SST通过第二步：利用STFT对时间求偏导来计算时频重排的瞬时频率估计算子。

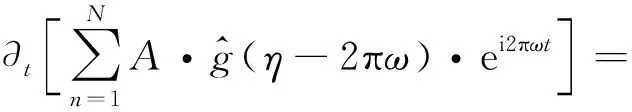
Sef(t,η)·i2πω

(5)

式中：∂为偏分符号；∂t为对时移变量求偏导。

当Sef(t,η)≠0时，信号f(t)的瞬时频率可以表示为

(6)

最后,通过同步压缩步骤将发散的能量聚集到估计的瞬时频率处

(7)

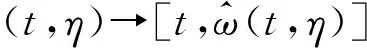
2 基于多重同步压缩变换的时频能量聚集谱诊断方法

2.1 多重同步压缩变换

通过压缩操作，提高了STFT时频图能量集中性。然而，为能准确提取复合故障特征(尤其是微弱故障特征)的最优解调频带，必须对时频图的能量集中性提出更高的要求。继续对SST的时频图进行压缩操作，则会得到能量更加集中的时频图。于是，通过多重压缩操作，来逐步提高时频图的能量集中性。多重同步压缩变换可表示为

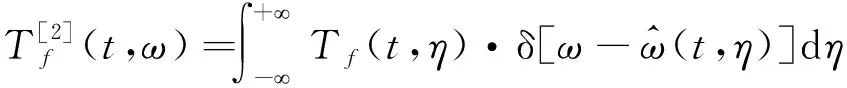
(8)

式中，K为迭代次数，K≥2。

接下来，将通过数学分析推导证明多重压缩是如何提高瞬时频率估计精度和能量聚集性。以单分量信号的2重压缩为例，将式(7)代入式(8)，表达式为

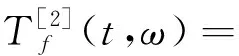
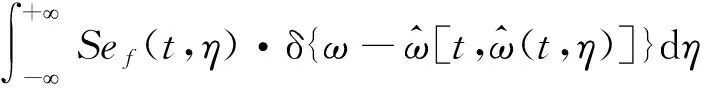
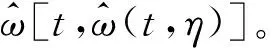
A(u)=A(t)，

式中，余项O[A′(t)]，O[φ‴(t)]被忽略。则信号f(u)可以表示为

(11)

假设窗函数为高斯窗函数g(t)=e-0.5t2，则信号f(u)的STFT为

e-0.5(u-t)2·e-i2πη(u-t)du=

(12)

然后将式(12)代入式(6)得到

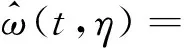
(13)

由于估计瞬时频率为虚数，取实部作为瞬时频率估计值。则1次压缩得到的瞬时频率估计值为

(14)

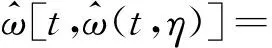
(15)

对1次、2次压缩后得到的瞬时频率估计误差进行对比

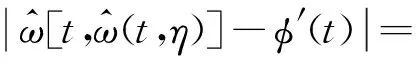
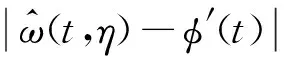
(16)

从式(16)可以看出，2次压缩后的瞬时频率估计值更接近真实瞬时频率，这也意味着能量更加集中。同理，可推导出N次压缩后的瞬时频率估计值

(17)

经过每一次的压缩，多重压缩变换将产生更精准的瞬时频率估计值，并根据估计值重新分配排列能量，则时频能量将逐步聚集。综上，通过多重压缩操作显著提高了瞬时频率估计精度以及能量集中性。多重同步压缩变换的另一种表达式为

(18)

重构公式为

(19)

从式(8)和式(17)我们可以看出，多重同步压缩变换是一种迭代算法，是在迭代过程中逐步提高瞬时频率估计精度和能量集中性。此外，更重要的是，从式(17)可以看出ω(t,η)(或能量集中度)与迭代次数N呈指数关系,ω(t,η)会随着N的增加快速上升，随后趋于平稳。瑞丽熵[22-23]是描述系统信息不确定性或随机性的量化指标，被认为是时频平面上信号信息量和复杂度的有效度量，从而可以进一步用来作为系统方程优化的目标或者参数选择的判据。因此，本文选取瑞丽熵作为优化目标和停止条件。瑞丽熵的计算公式为

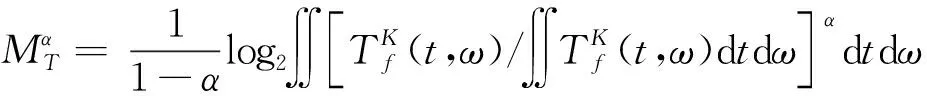
(20)

在本文中α=3。瑞丽熵会随着时频图能量集中度的提高而减小，即瑞丽熵会随着迭代次数的增加而减小。并且瑞丽熵与迭代次数之间仍呈现指数关系，即随着迭代次数的增加，瑞丽熵会快速下降，然后趋于平稳，收敛速度快。为兼顾计算成本和诊断效果，我们选取曲线中能在短时间内达到最理想效果的饱和点作为停止条件。

2.2 轴承复合故障时频能量聚集谱指标

多重同步压缩变化以高能量的形式在时频图中展示各复合(强弱)故障的共振频带及时间周期性，为从时频图中自动获取各故障的最优解调频带，提出能量聚集谱相对因子指标。

首先，对时频图中各瞬时频率处的能量进行包络解调，得到时频能量聚集谱，该聚集谱反映了各瞬时频率处能量的周期性。

其次，计算各能量聚集谱中的4种相对因子指标。不同故障对应的故障特征频率不同，即能量的周期性不同，因此可以通过聚集谱中周期频率的突显程度来分别选取各故障的共振频带。瞬时频率越接近最优共振频率，能量越高，则能量聚集谱中周期频率(故障特征频率)幅值越明显。我们通过设计相对因子指标来反应周期频率的突显程度。滚动轴承4种故障特征频率计算公式如下

(21)

式中：fr为轴承旋转频率(转速小波动下为其平均转频)；Dp为轴承节径；d为滚动体直径；θ为接触角；n为滚动体个数；fc，fo，fi，fel分别为保持架、外圈、内圈、滚动体故障特征频率。

由此，设计故障特征频率在能量聚集谱中的相对因子表达式为

(22)

(23)

(24)

(25)

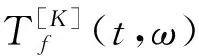
为准确输出信号中存在的故障特征，将得到的4条最优解调频带根据式(19)重构回时域信号，并计算相应的峭度值。在故障诊断中，我们一般认为峭度值低于3.5表示信号中不存在故障特征。因此，我们筛选出峭度值大于3.5 对应的最优解调频带[24]，即得到信号中存在的故障的最优解调频带，通过该操作实现复合故障的准确输出。

2.3 滚动轴承复合故障的时频能量聚集谱诊断方法

综上，本文方法的具体实施步骤为：

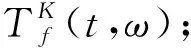
步骤2对时频图中各瞬时频率处的能量进行包络解调，得到能量聚集谱Sη，并根据式(22)～式(25)计算聚集谱的4种相对因子指标，通过指标最大化原则得到4条最优解调频带；

步骤3根据式(19)将4条最优解调频带进行重构得到时域信号，计算相应的峭度值，筛选出峭度值大于3.5对应的最优解调频带，即为存在故障的最优解调频带；

步骤4对各最优解调频带处的能量进行包络解调分析，得到能量聚集谱，根据谱线的分布情况进行旋转机械滚动轴承复合故障诊断。

3 试验验证

本文采用南京航空航天大学智能诊断与专家系统研究室的转子-滚动轴承试验台的滚动轴承故障数据进行诊断分析[25]。试验测试设备如图1所示，主要由综合电子控制系统、试验台、丹麦B & K公司4508型加速度传感器、东大仪器厂SE系列电涡流位移传感和NI公司USB9234数据采集器等构成。加速度传感器安装在左侧故障轴承座垂直(通道3)和水平(通道2、通道4)位置上，用于测加速度，位移传感器安装在右侧(通道1)位置，用于测转速。试验轴承型号为HRB6304，其规格列于表1。为模拟轴承复合故障，使用电火花线切割在外圈、内圈加工出宽度为0.6 mm的裂缝，滚珠切割出直径约1 mm，深度约2 mm的凹坑，如图2所示。

图1 滚动轴承故障模拟试验测试设备Fig.1 Fault simulation test equipment for rolling bearing

表1 HRB6304滚动轴承主要参数Tab.1 Main parameters of HRB6304 rolling bearing

图2 滚动轴承复合故障模拟Fig.2 Compound fault simulation of rolling bearing

设置采样频率为10 kHz，采样点数为4 096，选取转速为1 550 r/min的外圈、滚动体复合故障数据。根据转速和轴承数据，计算出外圈、滚动体的故障特征频率分别为66.306 Hz和89.986 Hz。振动信号1(外圈、滚动体)时域波形及频谱如图3所示。从图3(a)时域信号能看到存在冲击特征，但难以确定冲击周期。图3(b)频域中外圈、滚动体故障特征频率不突出。

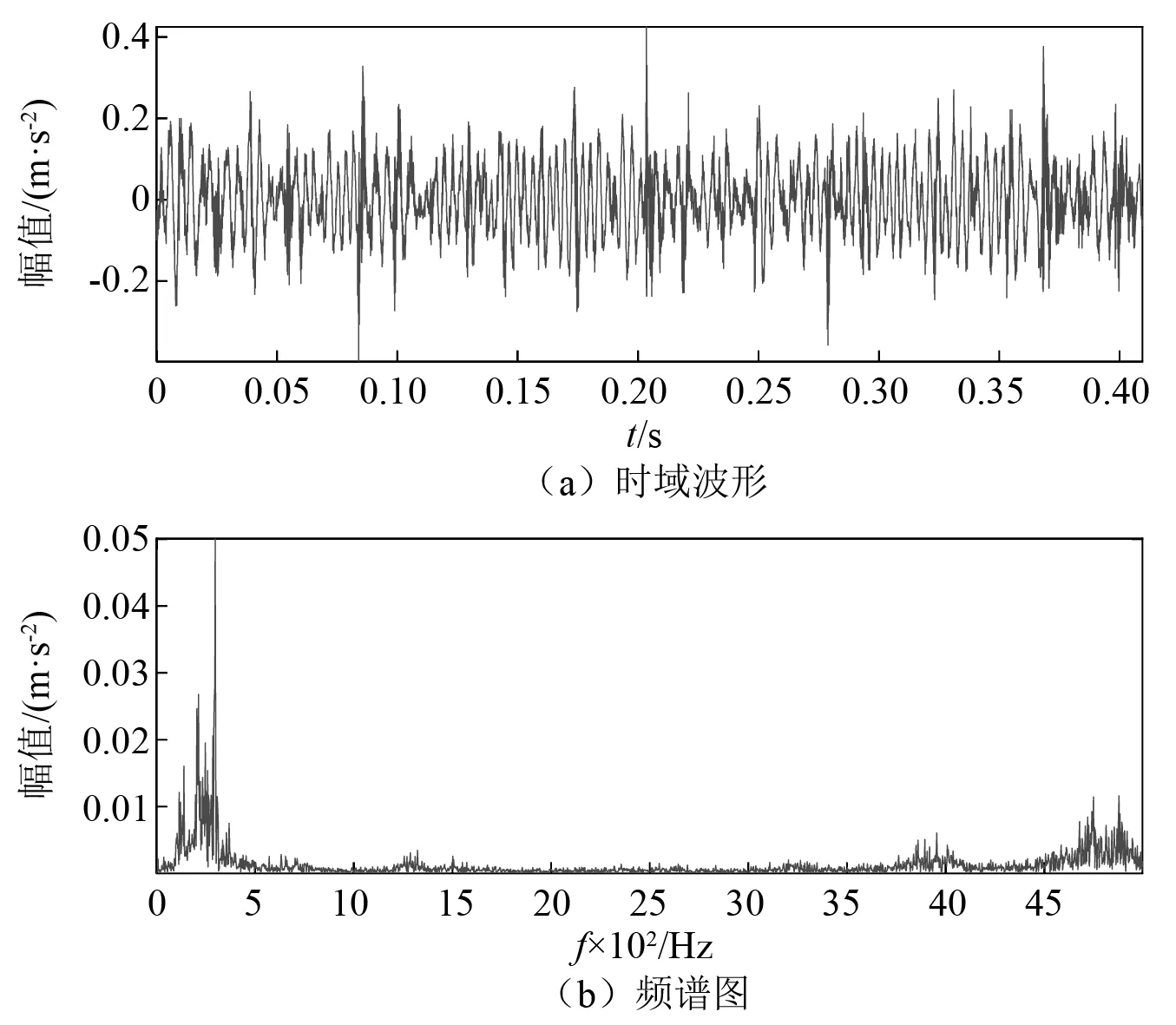
图3 轴承复合故障(外圈、滚动体)振动信号1Fig.3 Bearing compound fault (outer ring, rolling body) vibration signal 1

综合时频域，无法为轴承故障诊断提供可靠依据。因此，采用时频能量聚集谱方法分析信号(邻域设为1 Hz)，输出结果如图4所示。图4(a)为外圈故障结果，从中可以清晰地看出外圈故障特征频率及其倍频。通常，相对于其他轴承元件，外圈固定不动，外圈故障产生的冲击信号传至安装在轴承座上的传感器路径相对较短，所受干扰较少，特征比较明显，易于提取。而内圈随转轴一起运动，内圈上的故障点相对传感器的位置也随之不断变化，振动信号在从内圈处传递至传感器的过程中会受到多种干扰。因此，内圈故障特征比较微弱，较难提取。相对于内圈，滚珠既有自转又有公转，它的故障特征信号在传递至传感器的过程中所受的干扰更多，故障特征更微弱，提取更困难。图4(b)为滚动体故障结果，其中幅值最高的为滚动体故障特征频率。该试验结果证明本文方法能同时有效提取滚动轴承外圈和滚动体复合故障特征。

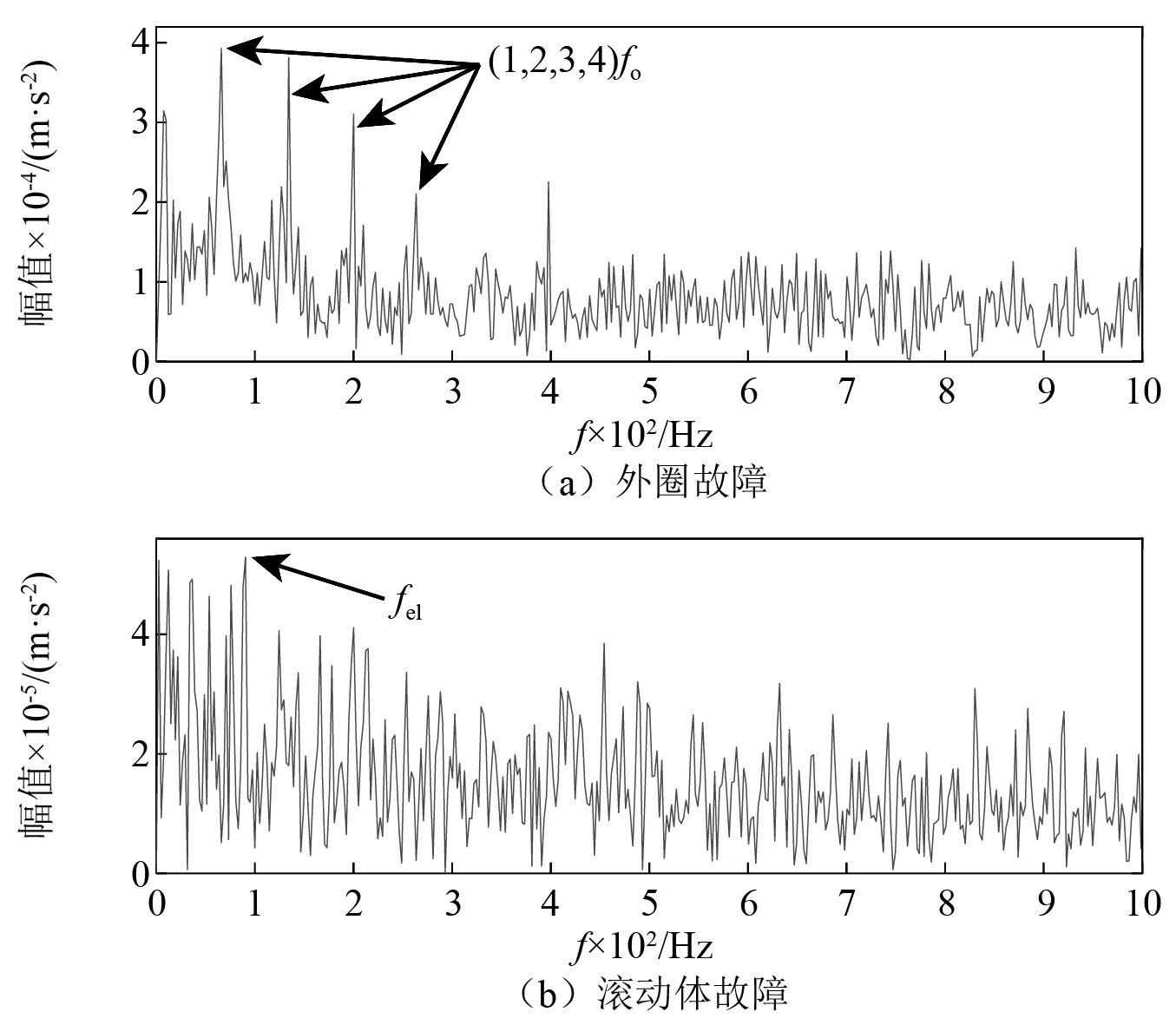
图4 时频能量聚集谱分析振动信号1的结果Fig.4 Results of time-frequency energy aggregation spectrum analysis of vibration signal 1

此外，我们还分析了振动信号1的瑞丽熵值与迭代次数的关系，如图5所示。从图5中可以看出，瑞丽熵随着迭代次数的增加而快速下降，然后趋于平稳。因此选择饱和点作为停止条件即兼顾了分析效果同时也兼顾了时间成本。

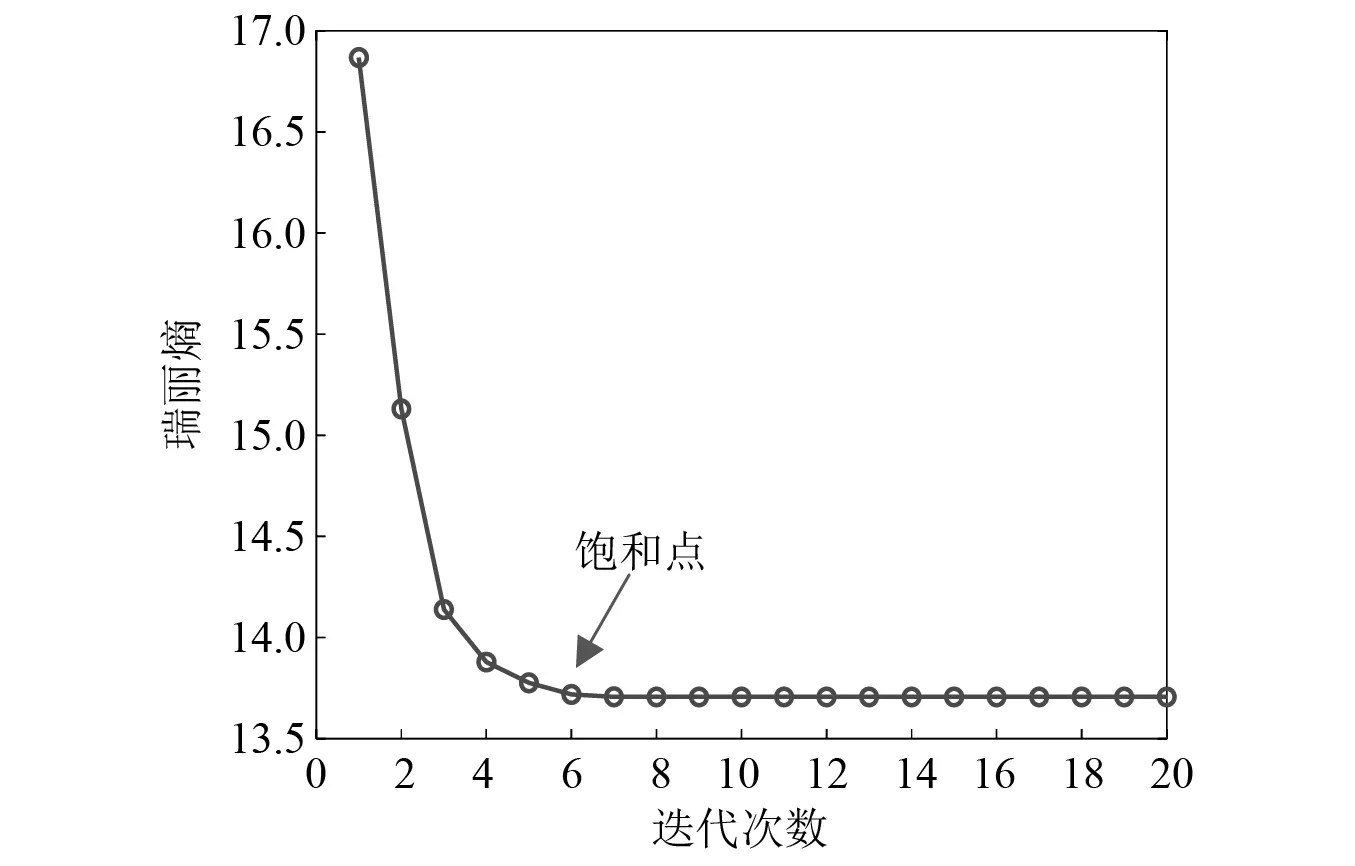
图5 振动信号1的瑞丽熵与迭代次数关系曲线Fig.5 The relation curve between Rényi entropy and iteration number of vibration signal 1

我们采用变分模态分解(根据文献[26]推荐，设置分解个数k为4，初始约束强度α为100)以及快速谱峭度(根据Antoni的推荐，分解层数设置为4。)作为对比方法，其结果分别如图6、图7所示。图6为变分模态分解的4个分量及对应包络谱，从分量C3，C4的包络谱中可以看到明显的外圈故障特征频率(圆圈标记)，但4个分量中都没有微弱的滚动体故障特征频率。同样，如图7所示，快速谱峭度只能提取出外圈故障特征频率(圆圈标记)，无法提取滚动体故障特征频率。

图6 振动信号1变分模态分解结果Fig.6 Results of variational mode decomposition of vibration signal 1

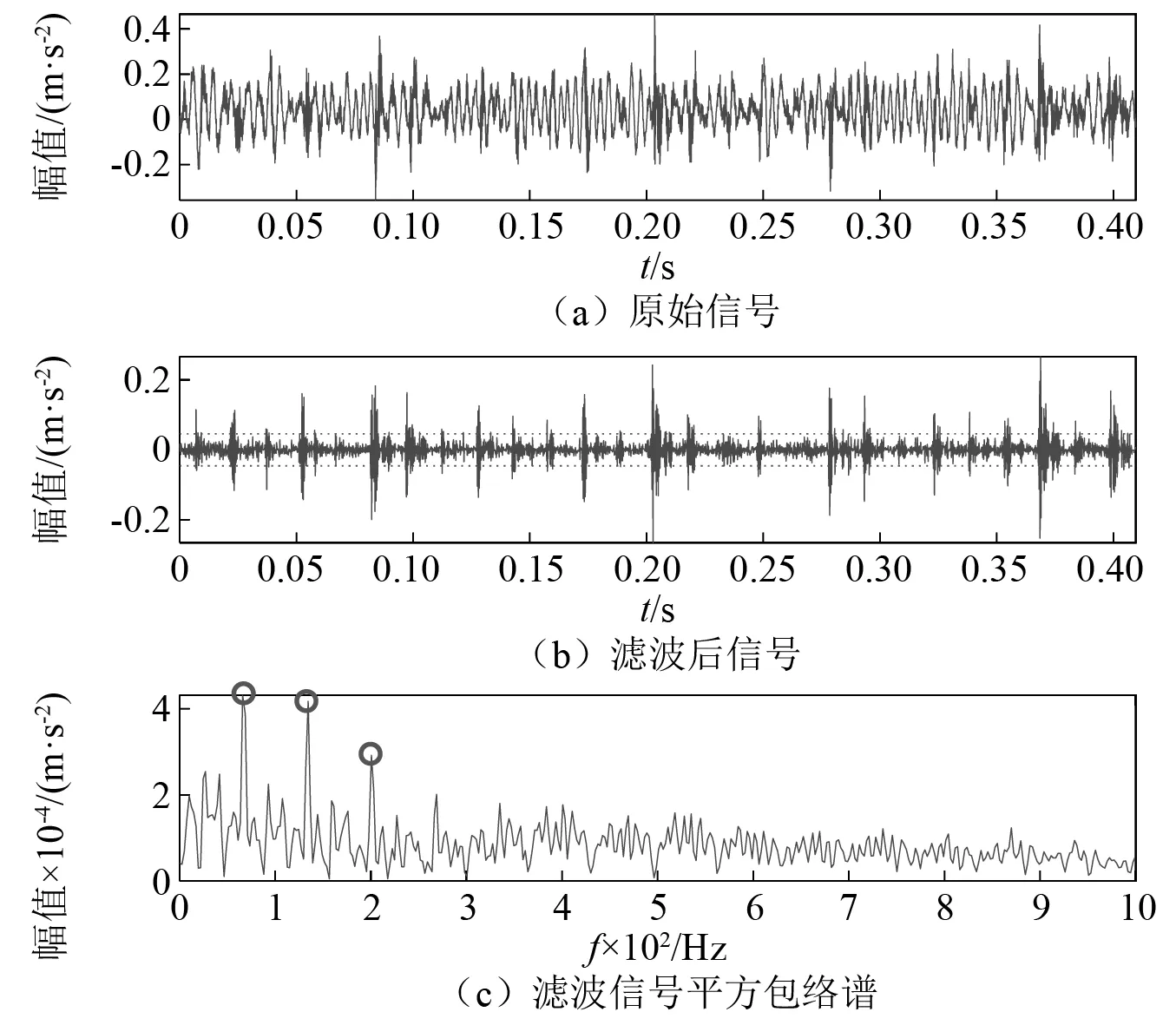
图7 振动信号1快速谱峭度分析结果Fig.7 Results of fast spectral kurtosis analysis of vibration signal 1

为进一步验证本方法对提取微弱复合故障特征的有效性，我们采用内圈、滚动体复合故障轴承进行测试。转速为1 481 r/min，则内圈、滚动体的故障特征频率分别为109.429 Hz，85.980 Hz。图8为振动信号2(内圈、滚动体)的时域图及频谱图。与图3相比，该故障信号更加复杂，干扰成分较多，从时域、频域很难得到与故障特征相关的信息。采用本文方法分析信号，其结果如图9所示。图9(a)为内圈故障结果，从中可以清晰的看出内圈故障特征频率及倍频，图9(b)为滚动体故障结果，从中可以清楚地看出滚动体故障特征频率。

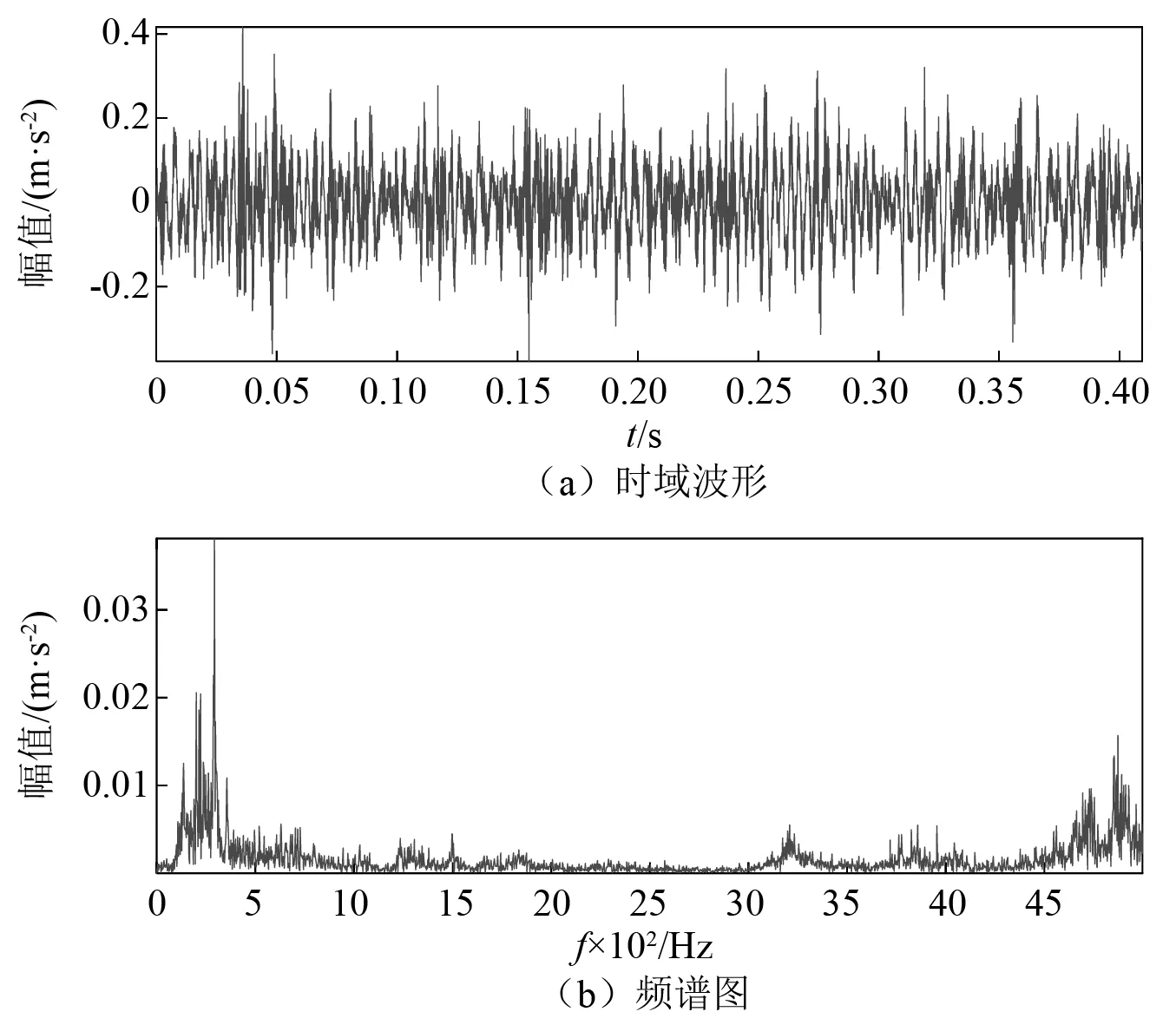
图8 轴承复合故障(内圈、滚动体)振动信号2Fig.8 Bearing compound fault (inner ring, rolling body) vibration signal 2

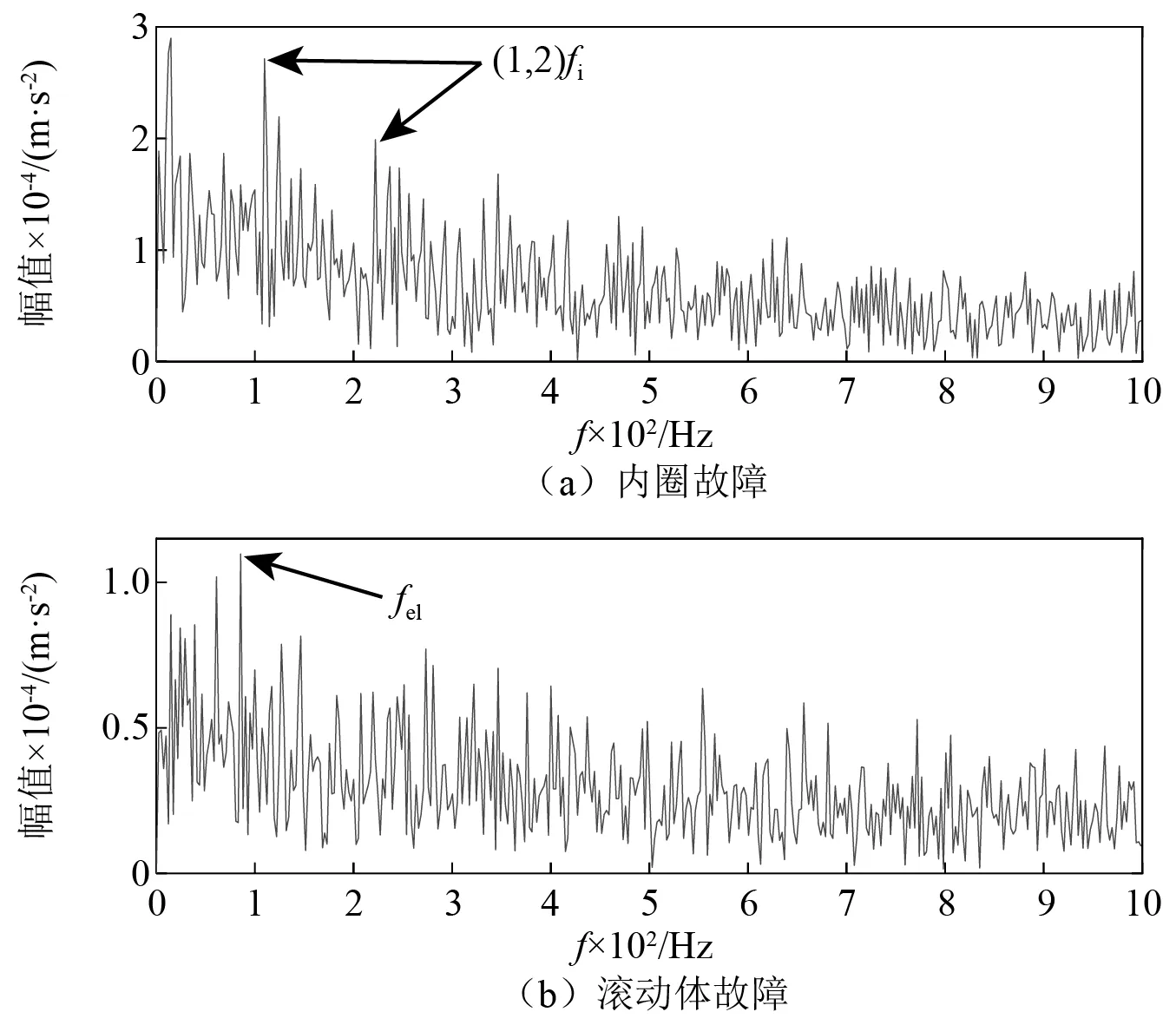
图9 时频能量聚集谱分析振动信号2的结果Fig.9 Results of time-frequency energy aggregation spectrum analysis of vibration signal 2

同样，采用变分模态分解、快速谱峭度方法进行对比分析，分别如图10、图11所示。在变分模态分解结果中，虽然在分量C2，C3中能找到内圈故障特征频率，但其幅值在包络谱中并不突出(圆圈标记)，而滚动体故障特征频率在4个分量中都没有出现。在快速谱峭度结果中，两种故障特征都不存在。综上分析，可见本文所提出的时频能量聚集谱分析方法可以有效提取滚动轴承强弱复合故障特征，能为轴承故障诊断提供可靠依据。

图10 振动信号2变分模态分解结果Fig.10 Results of variational mode decomposition of vibration signal 2

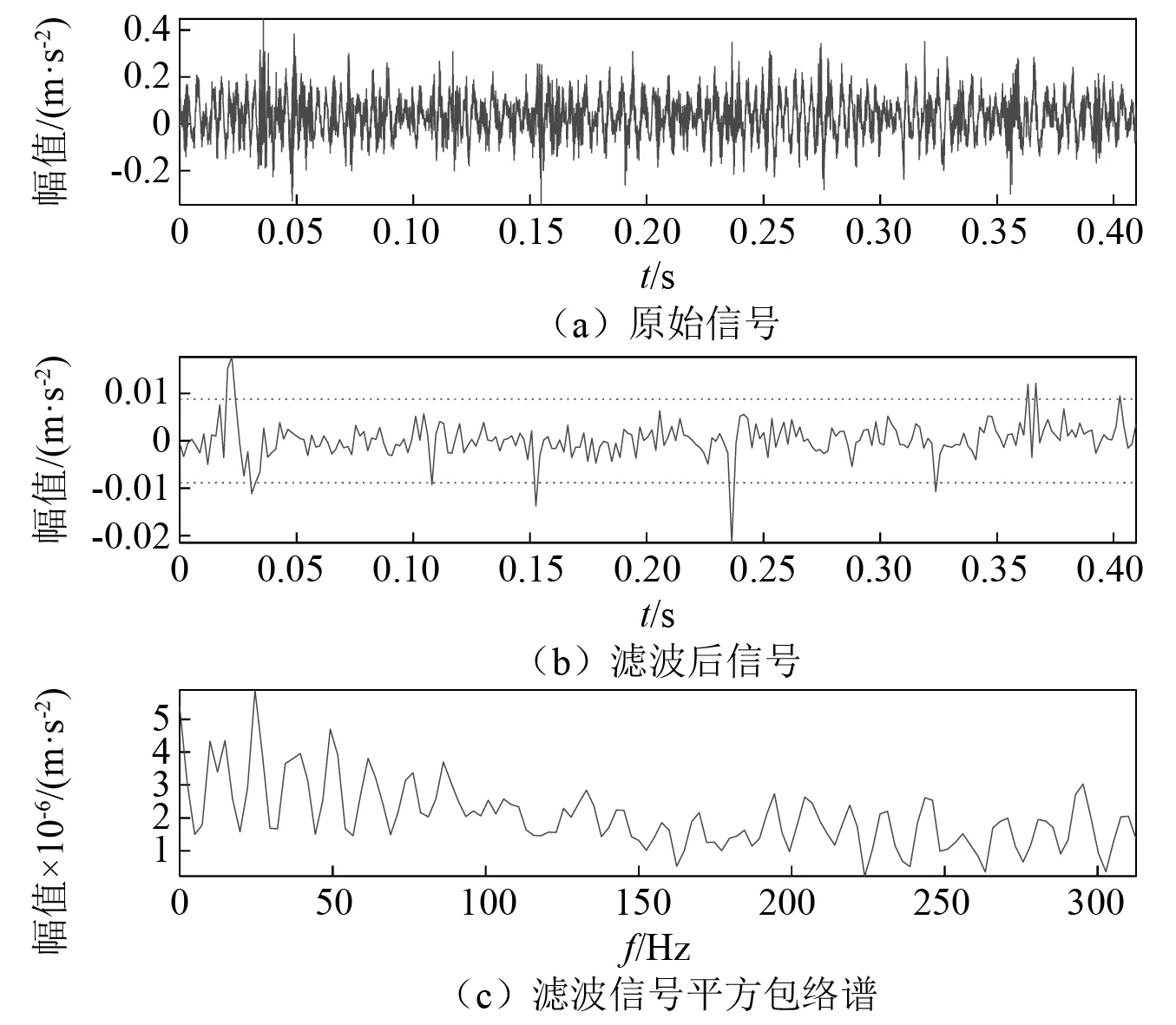
图11 振动信号2快速谱峭度分析结果Fig.11 Results of fast spectral kurtosis analysis of vibration signal 2

4 结 论

(1)针对旋转机械设备滚动轴承微弱复合故障特征难提取难点，提出时频能量聚集谱分析方法，将提取幅值特征转化为提取能量特征，有效凸显故障特征并降低特征提取难度。引入多重同步压缩变换，得到高能量聚集的时频谱图，为精准同步提取多条解调频带奠定基础。能量聚集谱指标能够准确选取各故障最优解调频带，实现多条最优解调频带同步输出，并为微弱和复合故障特征提取与识别提供有效的诊断手段。

(2)滚动轴承复合故障试验表明,本文方法不仅能成功提取故障特征明显的外圈故障特征频率，还能有效地识别出相对微弱的内圈、滚动体故障特征频率。与变分模态分解、快速谱峭度方法对比，结果充分验证了本方法的有效性，同时也证明了本方法在旋转机械滚动轴承故障诊断中的实践价值。