变幅频载荷下不同结构液阻衬套内特性的实测与计算分析

杨超峰， 周云郊， 黄翔龙， 李 锋， 李有意， 刘霏霏

(1.华东交通大学 机电与车辆工程学院，南昌 330013; 2.安徽中鼎减震橡胶技术有限公司，安徽 宁国 242300; 3.华南理工大学 机械与汽车工程学院，广州 510640; 4.中国第一汽车集团有限公司研发总院，长春 130013)

车辆底盘系统一般通过修改悬架衬套动力学特性对悬架侧振传递函数进行调整[1]。为控制来自路面、底盘结构局部共振、车轮摆振及轮胎空腔谐振等干扰激励引起的振动及噪声，封装液体刚度可变的橡胶衬套在底盘悬架、副车架及扭力梁等与车身的连接中得到了广泛的应用[2-4]。液阻衬套(hydraulically damped bushings，HDB)的外部动力学特性是橡胶高分子材料的力学特性、液体压强、液体流阻及液体流动速度的耦合动力学特性的集中表现。研究不同结构液阻衬套外部动力学随不同加载频率及振幅的变化与液阻衬套内部特性的耦合响应关系，有助于阐释液阻衬套工作过程中内特性非稳态动力学特性的作用机理。

Chai等[5]采用集总参数模型的方法对一种双工作悬置主簧结构式液阻装置的动特性进行了分析，并采用曲线拟合及奈奎斯特图分析的方法进行了模型参数的提取。Singh等[6]及Geisberger等[7]采用试验的方法对液阻悬置的体积刚度、惯性通道内的阻尼特性及流量阻尼系数进行了测试。Shangguan等[8]采用流-固耦合(fluid structure ineraction,FSI)的方法对液阻悬置的主要物理参数进行了计算分析。Fredette等[9-10]采用多参数集总参数模型及试验对比的方法，建立一种液阻衬套非线性流阻辨识参数模型，并对变幅频正弦及阶跃激励下模型的动特性进行了计算分析。因液阻衬套与悬置作用机理不同，悬置模型不能直接应用于液阻衬套的分析[11-12]。液阻衬套的内特性如液室的压强与流速与衬套的结构密切相关，内特性的变化直接影响液阻衬套薄泵液膜片变形量、泄流阀片开闭时刻及密封筋渗流等关键设计参数，对衬套的动力学特性及耐久性能有重要影响。现有文献对液阻衬套结构改变下的内特性与动力学耦合影响研究较少。

本文采用计算与试验对比的方法对不同结构式液阻衬套进行分析，首先设计并制作了多种结构类型液阻衬套的样本，测试得到液阻衬套的静、动特性的变化特性，验证了不同结构液阻衬套样本性能的一致性，并测试了液阻衬套内特性在不同振幅及频率激振下的响应。建立了一个统一的多惯性通道-多节流孔式液阻衬套的参数模型，推导得到内特性的统一表达式，采用计算与试验对比的方法验证了模型的正确性。最后采用直接耦合方法(也称为双向流固耦合法[13])计算得到不同结构式液阻衬套的内特性能变化的结果，并对不同振幅、不同频率激振下不同结构液阻衬套的液室平均压力波动量、不同结构液体通道内的平均压力波动、不同结构液体通道内的液体的流动速度及不同结构液体通道内的流量等参数进行了量化对比分析。试验及理论分析进行对比，验证了计算的正确性，阐释了多惯性通道-多节流孔式液阻衬套的作用机理，为液阻衬套的前期设计提供参考依据。

1 不同结构液阻衬套动态特性及内特性的测试结果与分析

1.1 不同结构液阻衬套样本

某车辆控制臂液阻衬套的剖解结构，如图1所示。金属外管与金属内管之间的橡胶主簧与金属外管之间形成两个液室，液室内充满配比液体。上、下两液室通过惯性通道或节流孔口道相连接。流道板与金属外管通过铆接密封形成惯性通道或图2中的孔口通道。

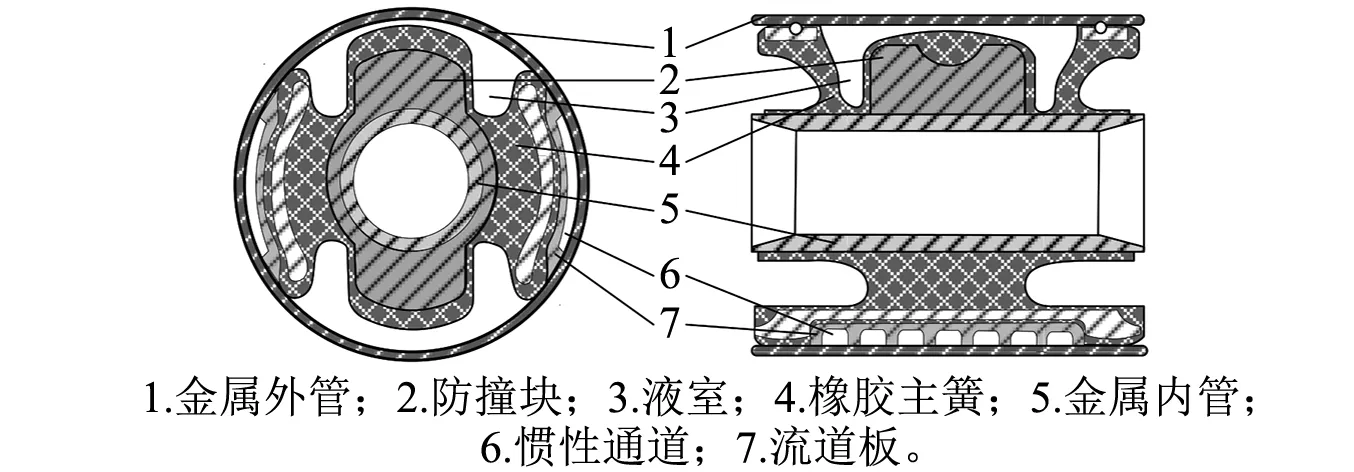
图1 液阻衬套的剖面图Fig.1 Sectional view of HDB

图2 液阻衬套的流道板Fig.2 Runner plate of HDB

为得到液阻衬套的不同结构，通过改变流道板的不同组合形式，制作了15个样件，编号采用HDB1～HDB5进行描述，HDB1～HDB5每种样本做了同样3个，HDB1～HDB5放掉阻尼液体得到结构HDB6。对应样本的结构组合如表1所示。

表1 HDB样本的不同结构组合Tab.1 Different structural combinations of HDB samples

单惯性通道HDB1为堵塞一边惯性通道流道板式的液体流道；双惯性通道HDB2为对称安装两个液体通道式的流道板；无通道HDB3为堵塞两边流道板的液体通道；惯性通道+节流孔式HDB4为一边安装惯性通道式的流道板，对称安装孔口式的流道板；节流孔+节流孔式HDB5为对称安装两个孔口式的流道板；橡胶主簧HDB6为放掉对应液阻衬套内的液体。

采用MTS831弹性动态特性振动试验台测试不同结构HDB的动态特性，动特性采用动刚度及滞后角进行表征。

液压衬套的结构及材料参数尺寸，如表2所示。

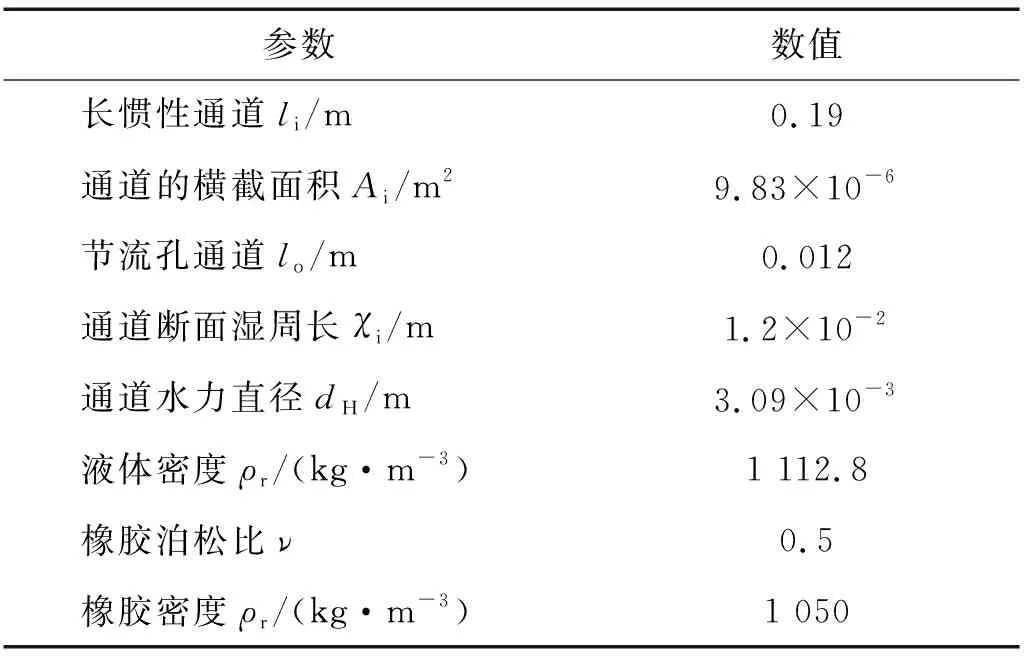
表2 液压衬套的结构及材料参数尺寸Tab.2 Geometric and material parameters of HDB

1.2 液阻衬套内特性测试

制作测试内特性的试验夹具，定制压力传感器，弹性振动试验台MTS831与eDAQ进行数据传输。采用Somat 软件进行数据的提取及处理。试验测试如图3所示。

图3 内特性的测试Fig.3 Test of internal characteristics

1.3 液阻衬套动特性的实测结果与分析

不同结构HDB在387 N相同预载荷下的平均静刚度测试值在463±10 N/mm内。表明不同结构HDB的性能具有一致性，所以在实测结果的对比研究中，同一种结构的HDB仅展示出一个样本的测试结果。

不同结构HDB的动特性如图4所示， HDB1～ HDB5的动刚度-频率曲线都具有随激振的不同频率及振幅变化的特性，HDB1与HDB2分别具有不变特征点M1及M2，M1及M2随激振振幅的变化，基本位置不变。随频率的增加，HDB4与HDB5也具有不变特征点。具有不变特征点是液阻型橡胶隔振器各个参数调整到最优的一个表征。

当激振频率大于60 Hz后，HDB1，HDB2，HDB3与HDB6的滞后角类似，与HDB3实测数据结果对比，表明激振频率下大于82 Hz后，HDB1，HDB2的动特性能与HDB3重合，表明流道“锁止”。

1.4 液阻衬套内特性的实测结果与分析

液阻衬套内特性的测试结果如图5所示。测试的激励振幅PP=0.1 mm，PP=0.3 mm，PP=0.6 mm及PP=1.0 mm，激振频率范围为0～50 Hz。

图5 HDB内特性的测试结果Fig.5 Test results of internal characteristics of HDB

由图5可见，液室内的压力-频率曲线随激振振幅的增大，液室内压力增加。随激振频率的增加，液室内的压力增加，达到峰值，而后逐渐减小。结果表明，在液柱共振频率段附近，由于液阻的影响，液体通道内流液体流量减少。导致液室内压力值达到最大。

2 不同结构多通道式液阻衬套动力学特性及内特性的集总参数模型

2.1 动力学特性的集总参数模型

由于集总参数模型中的物理参数可清晰对应表征HDB具体的物理意义，工程上多采用集总参数模型对HDB实物性能进行快速分析。本文推导了一种统一的多惯性通道-多节流孔式的集总参数模型对HDB1～ HDB5的性能及内特性进行描述。

统一的多惯性通道-多节流孔式的集总参数模型，如图6所示。Kr，Br分别为HDB橡胶主簧的动刚度(N/m)及阻尼系数(N·s/m)，Kr等于Kr1与Kr2之和；Br等于Br1与Br2之和；Ap1，Ap2分别为两液室的等效活塞面积，m2；P1(t)，P2(t)分别为两液室内的平均压力波动量, (N/m2)；两液室的体积变形量分别用体积刚度K1及K2(N/m5)表征，液室体积柔度C1和C2的倒数分别为K1及K2；Qi(t)，Qo(t) 分别为流经不同通道的液体流量,(m3/s)[14]。

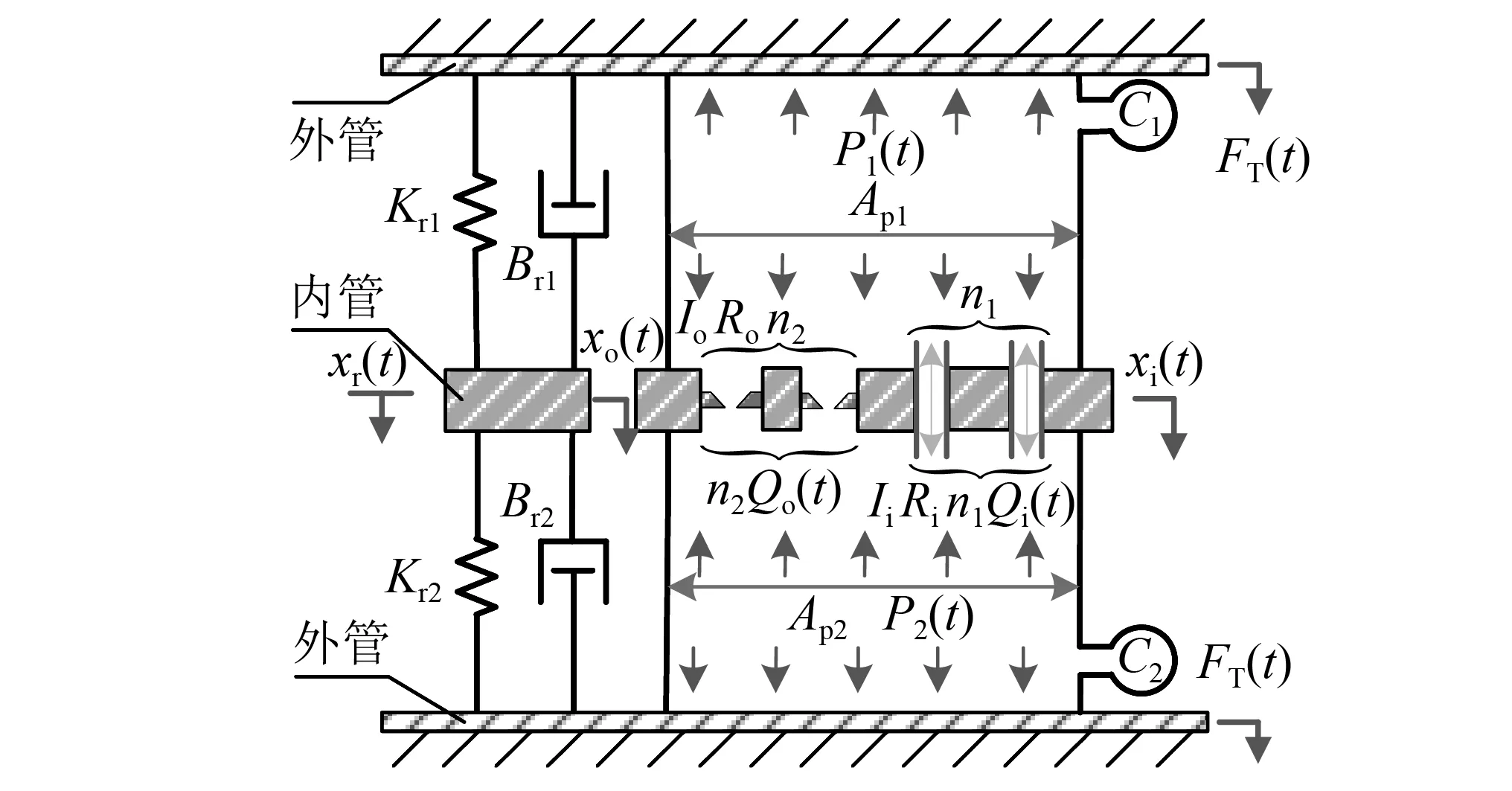
图6 统一的多惯性通道-多节流孔式HDB的集总参数模型Fig.6 The unified multi-inertial channel-multi-orifice HDB lumped parameter model

模型通道假设一列由n1个相同的惯性通道构成，其长度与面积定义为li及Ai；惯性通道内液体流动的惯性系数采用Ii表示；Ri1与Ri2分别为由于惯性液柱在通道内流动的沿程损失所产生的线性与非线性的流量阻尼系数；另一列由n2个相同的节流孔口型液体通道构成，其长度与面积定义为lo及Ao；Io为孔口通道中液体质量的惯性系数；R01与R02分别为由于液柱在孔口流动的局部损失所产生的线性及非线性阻尼系数。xi(t)为液柱相对通道壁面移动的位移,m；正弦位移激励xr(t)=Xrsin(ωt)加载在内套管上；外管响应力值为FT(t)。

依据假设，取系统的状态变量为XT=(x1,x2,x3,x4)= (P1,P2,Qi,Qo)，系统的状态方程为

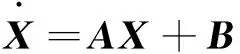
(1)

式中，A与B的表达分别为

(2)

(3)

传递到外管的力为FT(t)

(4)

(5)

其中，

M=Ap1K1+Ap2K2,Zi=Iis+Ri1,

Zo=Ios+Ro1,K=K1+K2

(6)

2.2 HDB内特性的集总参数模型

由图6可得，液体通道内液柱运动位移与流量的关系方程式为

(7)

统一的多惯性通道-多节流孔式HDB液体通道内流量-位移响应量的传递方程分别为

(8)

(9)

(10)

统一的多惯性通道-多节流孔式HDB两液室内压强-位移响应量的传递方程表达式

(11)

(12)

3 液阻衬套动力学特性及内特性的模型验证

3.1 HDB动力学特性的模型验证

准确的模型参数的提取是有效验证集总参数模型的基础。模型参数的提取一般有4种方法：①曲线拟合及奈奎斯特图；②试验方法，因HDB结构的复杂性，测试密封难以保证，采用试验方法进行模型参数的辨识较为困难；③不变特征点进行液阻衬套参数的辨识，具体可参考文献[15]；④FSI计算方法。

本文综合采用不变特征点及直接流-固耦合方法得到的模型参数，采用不变特征点及FSI计算辨识得到的主要参数(Ap1，Ap2，K1及K2)对比，如表3所示。具体参数辨识方法可参考文献[16]。采用不同计算方法得到参数差别小于10%，适于工程应用。

表3 辨识参数的对比Tab.3 Comparison of identification parameters

采用FSI计算得到不同HDB结构惯性系数及流量阻尼系数的对比，如表4所示。

表4 不同HDB结构惯性系数及流量阻尼系数的对比Tab.4 Comparison of inertia coefficient and flow damping coefficient of different HDB structures

计算得到的HDB1的动力学特性与试验值的对比曲线，如图7所示。由图7可见，对比结果验证了参数辨识的有效性。

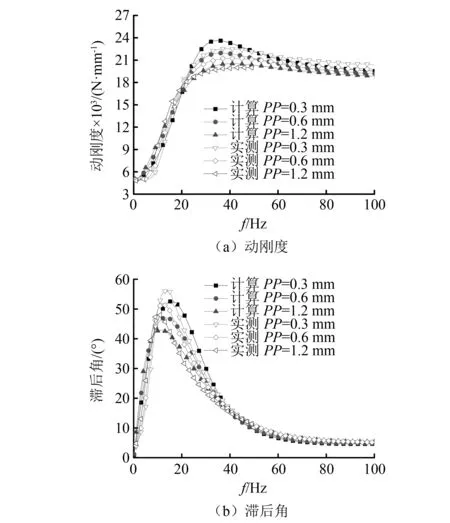
图7 HDB1动力学特性的计算值与试验值的对比Fig.7 Comparison of calculation and experiment of kinetic characteristics of HDB1

3.2 HDB内特性的模型验证

由式(8)～式 (12)，依据计算方法辨识得到的参数，采用Laplace变换，计算的内特性与试验值的对比，如图8所示。由图8可见，计算分析与试验数据吻合性较好。

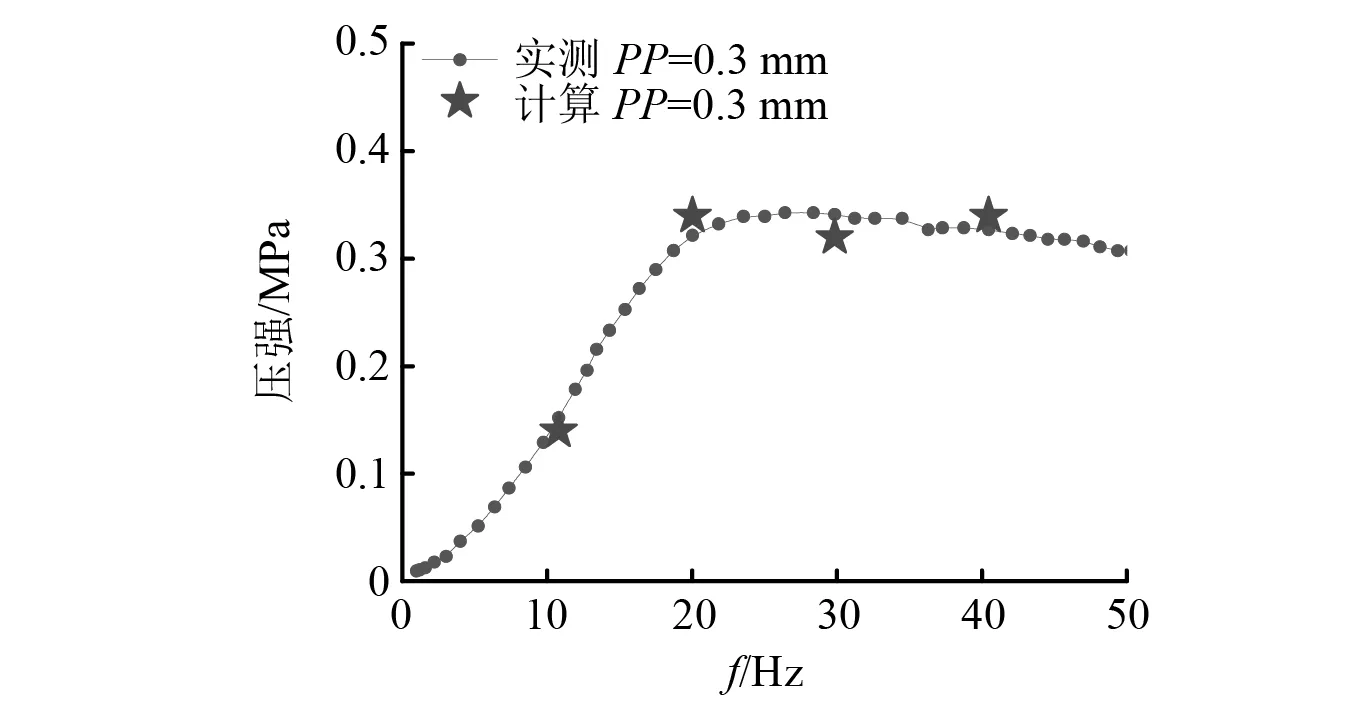
图8 HDB内特性计算与试验的对比Fig.8 Comparison of HDB internal characteristic calculation and experiment

4 不同结构及幅频激振下液阻衬套内特性的计算分析

4.1 不同结构HDB的压力与流速分布分析

以HDB1与HDB2为例，计算采用均匀分布压力对不同结构HDB模型两液室内的液室与液体通道内液体的平均压力分布进行分析。不同加载时刻t下，加载激振振幅PP=1.2 mm，加载激振频率为20 Hz，对比两种结构液体的压力分布如图9所示。由图9可见，在不同加载时间，不同流道结构下两液室的压力分布不均匀波动较小。表明HDB两液室泵液所排开及吸入的液体被同步排入或被吸入另一个液室，并没有引起两液室间的平均压力有较大的变化。但正弦加载激励下，液体通道内液体流动方向及状态随加载方向改变，通道内压力的分布波动较大。

图9 不同流道结构下液室与液体通道内液体的压力对比Fig. 9 Comparison of the pressure of the liquid in the liquid chamber and the liquid channel under different flow channel structures

加载激振振幅PP=1.2 mm，加载激振频率为20 Hz，对比不同流道结构下液体通道内液体的流动速度的变化，如图10所示。

由图10可见，在不同加载时间，液柱在惯性通道内来回流动。Y向内管激振加载点的最大平均流速为75.2 mm/s，HDB1与HDB2液体通道横截面Y向的平均最大流速分别为1 945.4 mm/s及1 584.3 mm/s。由于通道不同，HDB1通道内的液体平均最大流速比HDB2大18%。与加载点平均速度相比较，HDB1与HDB2液体通道内液体流速被放大的倍数分别为26及21。所以HDB可被称为“流速度放大型吸振器”。

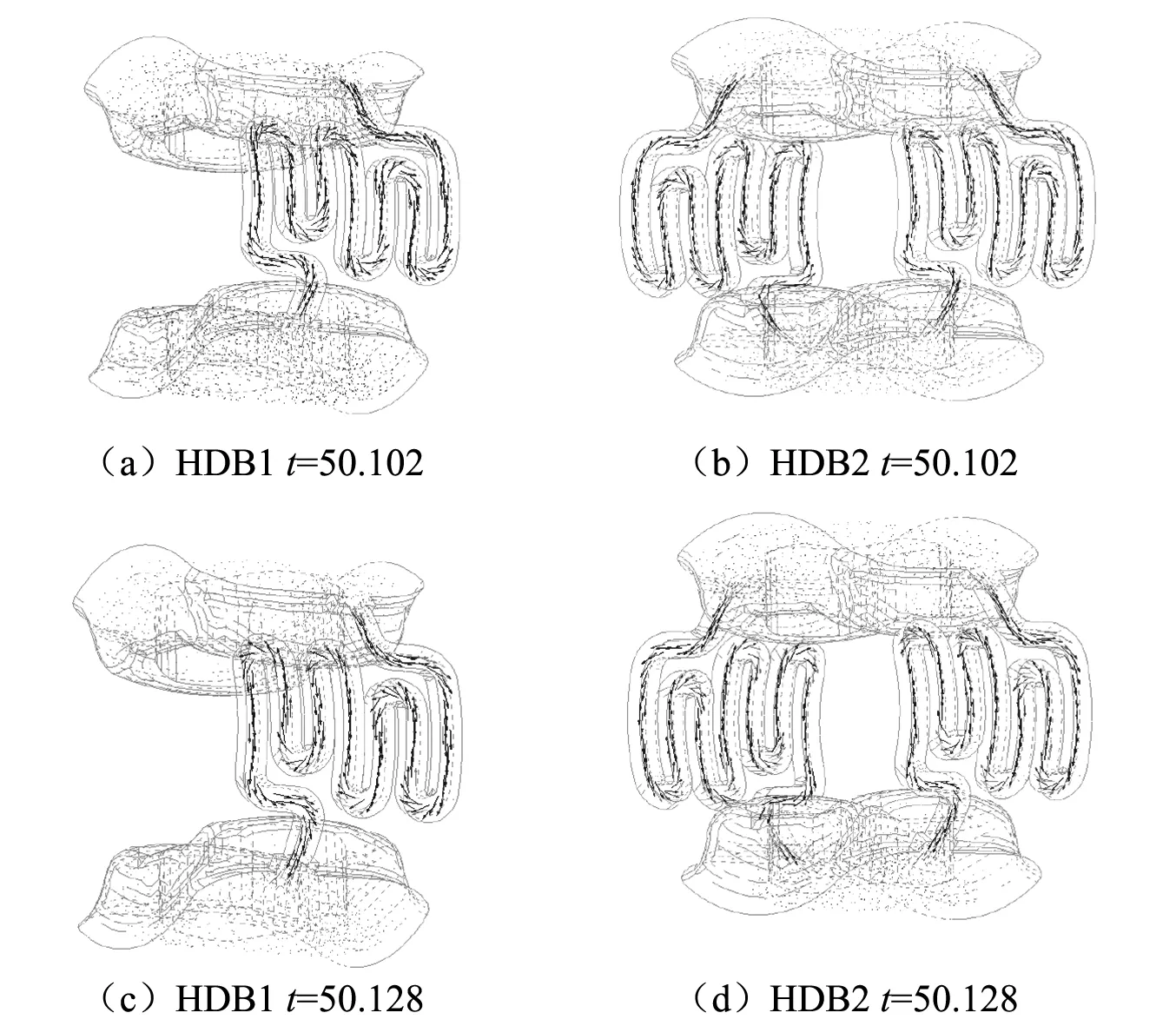
图10 不同流道结构下液体通道内液体流动速度的变化对比Fig.10 Comparison of changes in liquid flow velocity in liquid channels under different flow channel structures

不同结构液室平均压力最大值及通道内最大流速最大值的对比，如表5所示。由表5可见，HDB1的液室最大平均压力最大，而HDB5最大压力最小，相对应，不同结构通道内液体的最大流速HDB1最大，而HDB5最小。表明一定情况下液室泵液量随液体通道内单位时间内通道横截面积的增加，液体流动速度减弱。分析结果符合伯努利定理。

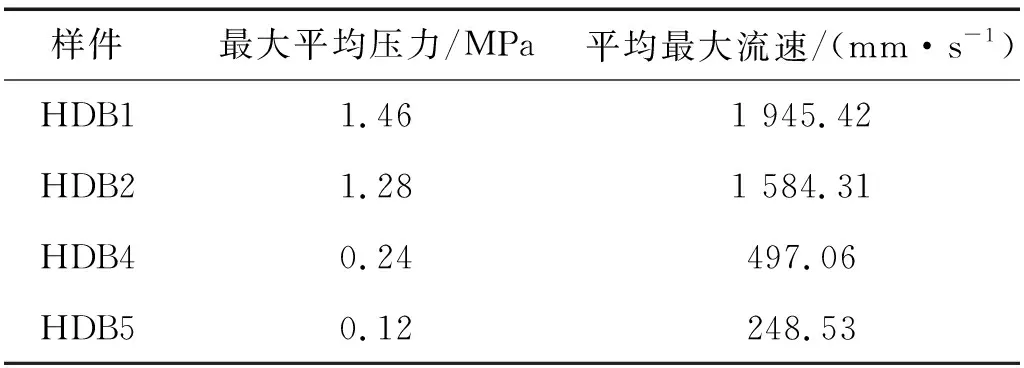
表5 不同结构下最大平均压力与最大流速的对比Tab.5 Comparison of maximum average pressure and flow velocity under different structures

4.2 同频不同振幅激振下HDB内特性的分析

以HDB2为例，加载激振频率为20 Hz，振幅分别为PP=0.3 mm及PP=1.2 mm工况下，在不同时刻t，上、下两液室的压力的变化，如图11所示。由图11可见，随激振振幅的增加，两液室内的压力变大。两液室内的压力值对应方向相反，大小相等，计算分析结果与式(11)及式(12)的理论分析相一致。

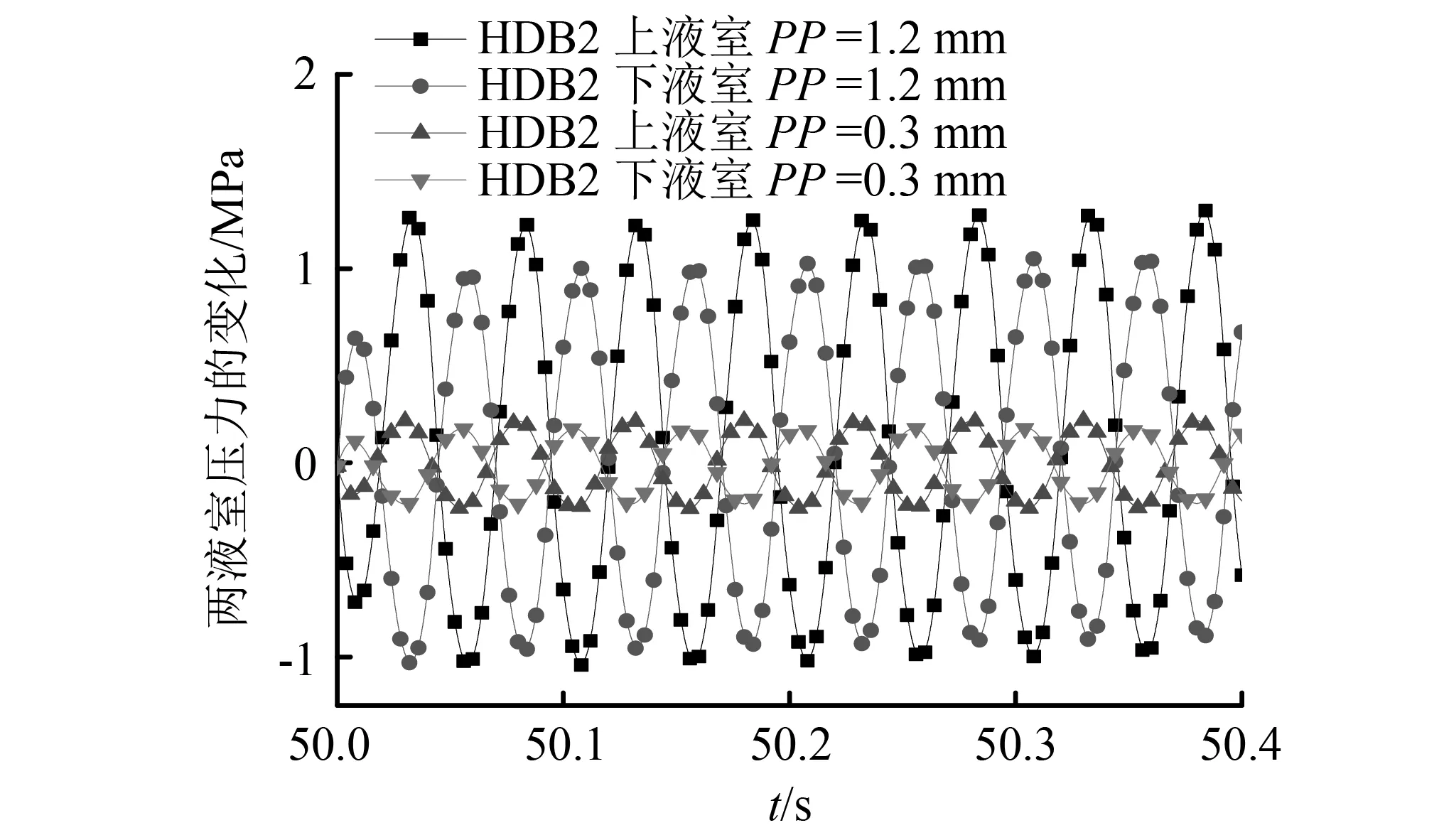
图11 HDB2液室内压力的变化Fig.11 The change of pressure in HDB2 liquid chamber

通道内液体的平均速度随加载时间的变化，如图12所示。由图12可见，两液体通道内液体的平均速度大小相同，表明两液体通道内的流动状态相同。随振幅的增加，通道内液体的平均速度增大。由于通道的横截面积相同，随振幅的增大，通道内通过液体的流量也增大。

图12 HDB2液体平均流度的变化Fig.12 Changes in the average fluidity of HDB2 liquid

HDB2在不同振幅激振下液室平均压力最大值及通道内平均流速最大值的对比，如表6所示。由表6可见，相同结构下(HDB2)，随振幅的增加，液室泵液量增多，液体通道内流量的增加，通道内液体平均流速最大值上升。表明，随激振振幅增大，液阻衬套漏液的风险也增大。

表6 不同振幅下最大平均压力与流速的对比Tab.6 Comparison of maximum average pressure and flow velocity under different amplitudes

4.3 同幅不同频率激振下HDB内特性的分析

以HDB2为例，加载振幅PP=0.3 mm，频率分别为20 Hz，120 Hz与300 Hz，在不同时刻，上、下两液室的压力随加载时间的变化，如图13所示。由图13可见，随激振频率的增加，单位时间内激振次数较多，液体质量由于惯性在通道内来不及转向流动，而“锁止”，产生流动延迟，导致上、下两液室内的压力及压力差变大。同激振频率下，两液室内的压力的值对应方向相反，大小相等。计算结果与理论分析一致。

图13 HDB2液室内压力的变化Fig.13 The change of pressure in HDB2 liquid chamber

随加载时间，通道内液体的平均速度变化，如14所示。由图14可见，随激振频率的增加，惯性通道内液体的平均流动速度减少，表明惯性液体通道趋于“锁止”。同幅激振工况下，20 Hz激振下的液体速度与300 Hz激振下的液体平均速度之比大于1.7。

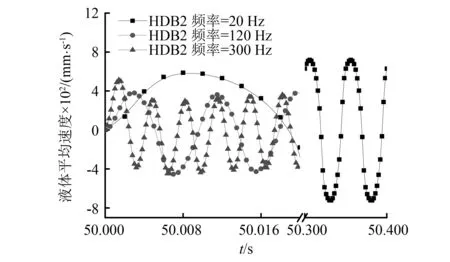
图14 HDB2液体平均流度的变化Fig.14 The change of the average fluidity of HDB2 liquid

振幅相同，不同激振下液室平均压力最大值及通道内平均流速最大值的对比，如表7所示。由表7可见，相同结构下，随频率的增加，液体通道内流速减小，引起通道的“锁止”，液室内的平均压力上升。表明，随激振频率增大，液阻衬套漏液的风险增大。

表7 不同频率下最大平均压力与流速的对比Tab.7 Comparison of maximum average pressure and flow velocity under different frequencies

4.4 结构不同对HDB内特性影响的分析

对HDB1，HDB2，HDB4，HDB5及单节流孔口通道式HDB等不同结构为分析对象。加载激振频率为20 Hz，振幅PP=1.2 mm。在不同时刻，液室的压力变化如图15所示。由图15可见，HDB1液室内的压力值最大；HDB2液室内的压力值次之；单节流孔口通道HDB液室内的压力值与HDB4液室内的压力值接近；HDB5液室内的压力值最小。由于液体通道横截面积Ai及长度li的改变，液体通道内液柱质量及局部损失所产生的线性及非线性阻尼的不同引起。

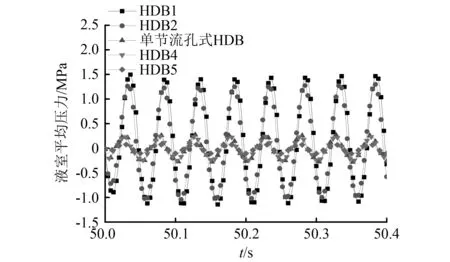
图15 不同结构HDB液室内压力的变化Fig.15 Pressure changes in HDB chambers of different structures

加载激振频率为20 Hz，振幅PP=1.2 mm。在不同时刻，不同液体通道内流量的变化，如图16所示。由图16可见，单节流孔口通道内液体流量值最大，流量值与HDB4节流孔口通道内的流量值相接近，HDB4惯性通道内的流量最小，表明HDB4液室内的液体主要通过节流孔口通道来回震荡产生大阻尼，其动特性与具有单节流孔口通道式HDB类同。由于通道数目的不同，与单孔口通道相比，HDB5节流孔口通道内液体的流量较小；对比HDB1，HDB2与HDB4惯性通道内液体的流量，HDB1通道内液体的流量最大。

图16 不同结构HDB液体通道内流量的变化Fig.16 Changes in flow rate in HDB liquid channels with different structures

加载激振频率为20 Hz，振幅PP=1.2 mm时。在不同时刻，不同液体通道内的平均压力变化，如图17所示。由图17可见，HDB1惯性通道内的平均压力波动量最大，HDB2液体通道内的平均压力波动量次之，但由于惯性通道内流阻的影响，HDB1与HDB2液体通道内的平均压力波动并不呈正弦分布，平均压力波动响应量有一定的滞后。HDB4节流孔口通道内的平均压力的变化与单节流孔口式HDB液体通道内平均压力的变化类似，由于液体分流作用，值较小。HDB4孔口通道内平均压力波动量的值最小。结果表明，HDB1惯性通道内液体的平均压力波动较小。

不同结构液室液室平均压力最大值及通道内最大流速最大值的对比，如表8所示。由表8可见，HDB1液室最大平均压力最大，HDB1次之。主要由于长惯性通道的流阻影响，惯性通道内流量与单节流孔HDB的流量相比较小约3.5倍；HDB4惯性通道内流量与其节流孔流量相比较少了近9倍，表明在此加载工况下，液体主要通过节流孔进行流动，长惯性通道流过的液体较少。表明相同载荷下，液体通道的结构改变对液阻衬套的内特性有较大影响。

5 结 论

(1) 对不同结构式液阻衬套在不同振幅及频率下的静、动特性及内特性进行了测试。结果表明，液体通道的结构、加载振幅及频率对液阻衬套的动特性及内特性都有较大影响。随频率的增加，液阻衬套液室内的压力波动先增大，后有平稳降低；随激振振幅的增加，液阻衬套液室内的压力波动具有增大趋势。

(2) 推导了一个可对不同结构进行描述的统一的多惯性通道-多节流孔式液阻衬套的集总参数模型。采用FSI计算及不变特征点相结合的方法得到计算的参数，验证了模型的正确性。

(3) 采用计算与试验对比的方法，对不同结构在不同振幅及频率激振下的内特性进行了分析，表明液阻衬套在激振下，液体通道内的液体速度被放大；相同频率下，随激振振幅的增加，通道内通过液体的流量增大；增加激振振幅及频率，液室内压强增加，液阻衬套漏液风险增大；相同载荷下，结构改变对液阻衬套的内特性有较大影响。