基于多层S型局域振子的声子晶体双层梁结构带隙特性研究

沈超明， 黄 杰， 陈墨林， 钱登辉， 王建春， 庄家威

(1. 江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212100; 2. 中国船舶科学研究中心, 江苏 无锡 214082)

减振降噪一直是工程界密切关注和着力解决的热点问题。振动噪声问题不仅会影响人员的身心健康，也会导致仪器疲劳损伤、缩短使用寿命，降低精密仪器的控制精度。传统的降低振动的措施主要包括抑制振源强度、隔振和消振。相对而言，从振动传播途径进行控制，实现振动的隔离、吸收，是减振降噪行之有效的方法，这也是工程应用中最常用的方法。在许多工程中梁类结构是经常遇到的一种基本构件，多年来一直是振动控制领域的主要研究对象之一。解决了梁类结构的减振问题，就意味着解决了许多工程中的减振问题。而声子晶体的振动带隙特性使得带隙范围内的振动被禁止传播或被很大程度的抑制，这为其在减振领域的应用提供了新的思路。

声子晶体[1-2]是一种人工周期性具有弹性波带隙的复合结构材料，近几十年来已经吸引了国内外学者的广泛兴趣。正是由于这类声子晶体结构具有的弹性波带隙特性，在减振降噪等应用方面存在很多潜在的可能[3-5]，可广泛应用于船舶、飞机、汽车以及大型发电机组等领域中。在现有的研究当中，主要存在Bragg散射[6]和局域共振[7]这两种带隙形成机制，并且前者带隙所对应的频段要比后者高2个数量级。研究表明，声子晶体梁板类结构同样具有带隙特性。因此，通过在一些基本弹性结构中引入声子晶体的设计思想，所构成的声子晶体杆[8-10]、声子晶体梁[11-16]以及声子晶体板[17-18]等结构也获得了一批学者的关注和研究。

Wang等对纵向弹性波在由周期贴附谐振子的细长梁所构成的准一维结构中的传播特性进行了研究。蒋泽等应用广义传输矩阵法(generalized transition matrix method,GT-MM)，建立了声波传播特性的理论分析模型，得到了其声波场的平面波解，给出了数值实现方案。研究表明，该方法可精确地模拟弹性波通过一维有限厚的周期结构、准周期结构以及完全无序结构的传播特性。Xiao等通过试验和理论相结合应用谱元法研究了带谐振器梁声子晶体的弯曲波传播特性。吴旭东等研究了周期数和晶格常数对双振子梁带隙特性的影响。杜春阳等设计了一种具有超阻尼特性的X形局域共振结构，并分析了周期性附加X形局域共振的梁弯曲振动传播特性。Li等应用行波法研究了空间变截面梁周期结构带隙特性。Chen等[19]提出了一种多目标优化的方法，采用径向基函数神经网络和有限元方法建立算法模型，并通过NSGA-Ⅱ算法求出最优解，优化结果表明，带隙宽度和衰减深度都明显增大。Chuang等[20]提出了一种利用自解调光纤布拉格光栅(self-demodulated fiber bragg grating，SFBG)位移传感器提取扭转带隙和瞬态扭转波的测量方法，并通过反射射线矩阵法(method of reverberation-ray matrix, MRRM)验证了扭转带隙和瞬态扭转波提取方法的可行性。Jiang等[21]提出了一种折叠压电声子晶体梁模型，能同时实现布拉格和局部共振带隙，获得了具有较强衰减特性的低频和宽频带隙。

在实际应用中，不存在无限长的梁结构，但无限周期结构的带隙频段和有限周期结构的衰减频段相吻合。因此本文建立了有限周期的声子晶体梁结构模型，计算振动传递损失，验证无限周期结构色散关系(能带结构)计算的准确性。笔者对现有形式材料各异的声子晶体梁结构带隙特性研究的基础上，先设计了一维折叠式S型周期振子，然后取8个单元振子竖向周期排列，并在其上下方贴附上板和下板，构成一个新的晶胞。再以新的晶胞横向周期排列，从而构造声子晶体梁结构，相当于声子晶体中嵌套声子晶体，相对传统声子晶体梁而言，将会产生更低频的禁带特性。采用有限元法计算能带结构，研究其带隙的形成机制和调节规律，并通过与相应单层结构的带隙特性进行对比，研究了单/双层的通性以及双层梁结构的特性，以及各参数对声子晶体梁结构带隙衰减频段的影响规律。

1 模型和方法

根据局域共振声子晶体结构带隙形成机制，建立了S型振子结构，其结构示意图如图1(a)所示。从图中可以看到，图1(a)通过3块钢板和2个复合块交错贴附而成，其中上下两块钢板为尺寸材料完全相同的薄板，中间钢板为尺寸较厚的厚板，而复合块由橡胶-铅块-橡胶组成。取8个S型振子竖向周期排列作为夹层，在其上下方贴附上板和下板，构成一个新的晶胞，其结构示意图如图1(b)所示。将新晶胞横向周期排列，构成声子晶体梁结构，如图1(c)所示。在结构模型中，晶格常数、上下板的厚度、S型振子薄板的厚度、橡胶层的厚度、以及铅层的厚度、S型振子厚板的厚度和单元振子总高度分别为a，e，h1，h2，h3，h4和h，一个单元的S型振子，长度和宽度分别为l和m，如图1所示。在结构模型中，各几何参数如表1和表2所示。

表1 计算所用到的材料参数Tab.1 Materials’parameters used in calculations

表2 计算所用到的几何参数Tab.2 Geometric parameters used in calculations 单位：mm

图1 结构模型Fig.1 Models of structure

对于单元振子的能带结构，采用有限元法来计算，并借助于商业软件COMSOL Mutiphysics来实现，对于有限元网格的划分，均采用四面体网格。对于S型振子的边界条件，非接触面均采用无压力自由边界条件。而相邻的振子交界面则采用Bloch-Floquet定理导出的周期边界条件，即

u(z+a)=u(z)ei(k·a)

(1)

将周期边界条件式(1)代入自由振动的有限元特征方程中，可以得到

Ku=ω2Mu

(2)

式中，刚度矩阵K和质量矩阵M均含有Bloch波矢相耦合的项，与传统有限元特征方程中的刚度矩阵和质量矩阵有所区别。式(2)是关于ω2的典型广义特征值问题对于每一个给定的Bloch波矢k，通过求解特征值，可得到相应的一系列特征频率。通过历遍所有的不可约Brillouin区边界上的波矢，最终可得到S型振子的能带结构。能带结构图中打开了较宽的带隙，因此在该带隙的频域内，处理工程上减振降噪的问题具有理论意义。将S型振子作为夹层置于上下板中形成新的晶胞，再以新的晶胞横向周期排列，从而构造可以处理工程上减振降噪声子晶体梁结构，如图1(c)所示，其晶胞结构如图1(b)所示。

由吴旭东等的研究可知，振子周期数的多少对带隙也有重要的影响。从理论上说，周期数越多其减振特性越好，而实际中由于结构尺寸的限制、轻量化要求等等，需要利用尽可能少的周期满足预期的减振效果，但最少需要2个振子，此声子晶体梁结构才能更好地利用S型振子的带隙特性实现减振效果。本文取8个振子竖向周期排列，并在其上下方贴附上板和下板，构成一个新的晶胞，其结构示意图如图1(c)所示。对于新的晶胞结构，同样采用有限元法计算，晶胞的边界条件，非接触面均采用无压力自由边界条件，而相邻的晶胞交界面采用Bloch-Floquet定理导出的周期边界条件。与S型振子计算方法同理，可得到该新晶胞的能带结构。

2 数值结果和分析

2.1 S型振子能带结构及传输曲线

图2(a)给出了S型振子的能带结构，其中计算所用到的材料参数和几何参数分别如表1和表2 所示。为了验证计算所得能带结构的准确性，将8个振子竖向周期排列，并且将激励点和相应点分别放置在其最下方和最上方，如图3所示。计算得到相应的振动传输曲线，如图2(b)所示。

图2 S型振子能带结构和相应的振动传输曲线Fig.2 S-type unit cell band structure and corresponding transmission power spectrum

图3 由8个S型振子周期排列而成的振子结构模型Fig.3 The oscillator structure model is formed by the periodic arrangement of 8 S-typeunit cells

由图2(a)可以看到，S型振子能带结构在55～90 Hz打开了一条较宽的带隙，并且由图2(b)可以看到，振动在有限结构中传递，传输曲线的衰减频域也非常宽，且大致与能带结构相对应。这与已有研究中所得的无限结构的带隙频段和有限结构的衰减频段相吻合这一结论相符合。S型局域共振型振子如此低频的带隙，对实现特定频率范围的低频减振降噪有十分可观的应用前景。为了揭示其带隙特性，提取了能带结构图中临界点的特征模态相对应的位移场，如图4所示。

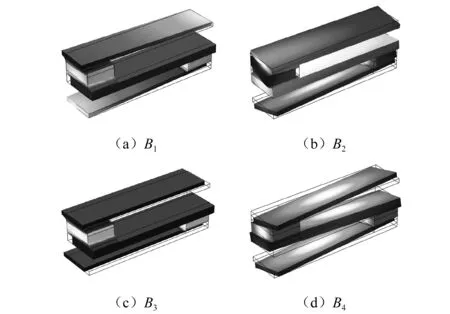
图4 与图2(a)中标注的特征模态相对应的位移场Fig.4 The displacement fields of eigenmodes labeled in Fig.2(a)

在S型局域振子的能带结构中，对于模态B1和B3，位移场为钢板作纵向振动，铅块保持静止，其中上下两块钢板向内振动的相位与中间钢板向外振动的相位达到纵向振动动态平衡。对于模态B2和B4，位移场都有一定程度的扭转振动。但不同的是，在模态B2中，为中间钢板保持静止，铅块和上下钢板作一定程度的扭转振动。在模态B4中，铅块保持静止，上中下三块钢板作一定程度的扭转振动。这些模态耦合作用的结果，一条频率区间为55～90 Hz的振动带隙被打开。通过计算振动传输曲线，其中振动衰减频段与带隙范围基本吻合。

2.2 振子布置在单板上的能带结构及传输曲线

由8个S型振子和下板构成了新的晶胞，其能带结构如图5(a)所示，其中计算用到的材料参数如表1和表2所示。为了验证计算所得能带结构的准确性，再将8个晶胞横向周期排列，并且将激励点和相应点分别放置在如图6所示的位置，计算得到相应的振动传输曲线，如图5(b)所示。

图6 由8个晶胞周期排列而成的声子晶体单层梁结构模型Fig.6 Structure model of phononic crystal veneer beam composed of 8 unit cells arranged periodically

从振动传输曲线可以看到，并未出现明显的衰减频域。为了揭示其特性，给出了与图5(a)中标注的特征模态相对应的位移场，如图7所示。

图5 单层梁能带结构图和相应的振动传输曲线Fig.5 Band structure and corresponding transmission power spectrum of veneer beam

图7 与图5(a)中标注的特征模态相对应的位移场Fig.7 The displacement fields of eigenmodes labeled in Fig.5(a)

在局域共振型单层梁结构晶胞的能带结构中，对于模态D1和D2，位移场主要为沿z方向的垂直振动，中间振子基本保持静止。对于模态D3和D4，位移场为下板绕水平面内中轴线旋转振动，中间振子仍然基本保持静止。其中，这4个模态中，都是振动能量集中在一侧板，而中间振子和另一侧板基本保持静止。对于模态D5和D6，位移场为两个周期的S型振子产生振动，下板基本保持静止。这是因为模态D5和D6是能带结构图中临界点的特征模态相对应的位移场，所以中间振子开始存在小幅度的振动。

通过以上的带隙特性研究分析，可以知道衰减频域并未出现的原因。因为激励点和响应点都在下板时，结构中的振子并不能发挥作用，这也进一步证明振子对单层梁结构振动传递的影响很小。可见，声子晶体中带隙的产生是比较复杂的，它往往是在多种机理共同作用下产生的，并不是简单的附加振子就一定能产生带隙。

2.3 振子布置在双板上的能带结构及传输曲线

若将图5所示的声子晶体单层梁结构加以上层板，则可形成声子晶体双层梁结构。该双层梁结构的晶胞能带结构如图8(a)所示。其中，计算用到的参数与图5(a)所示的参数一致，具体如表1和表2所示。保持激励点位置不变，将响应点改变至上板位置如图9所示，得到的振动传输曲线如图8(b)所示。由图8(a)和图8(b)可以看到，其中振动衰减频段与带隙范围基本吻合。

图8 双层梁能带结构图和相应的振动传输曲线Fig.8 Band structure and corresponding transmission power spectrum of double-layer beam

图9 由8个晶胞周期排列而成的声子晶体双层梁结构模型Fig.9 Structure model of phononic crystal double-layer beam composed of 8 unit cells arranged periodically

图8(c)～图8 (e)分别给出了1～3个振子的声子晶体双层梁结构的振动传输曲线，图8(f) 给出了S型振子数量与最大衰减幅值的关系曲线。由图中可知，一个周期振子的声子晶体双层梁结构振动衰减很小，随着振子数量的增大，衰减越来越大，这点可以从振子数量与最大衰减幅值的关系曲线很直观地看出来，验证了吴旭东等研究结论的正确性。从图8(b)中可以看到，声子晶体双层梁结构的振动传输曲线的衰减频段与图2(b)的衰减带频率范围基本一致，且相对于图2(b)来说，具有更强的衰减特性。这是由于S型振子可以打开一条频率区间为55～90 Hz的带隙，激励从下板经过振子传递到上板，当频率落在振子的带隙范围之内时，通过振子传递的振动被抑制，从而使得图8(b)和图2(b)这两幅图中的振动衰减频带相同。因此，该双层梁中带隙的打开，实质上是S型周期振子发挥了作用。也就是因为声子晶体梁很好地利用到S型振子的低频禁带特性，从而形成了具有低频带隙的梁结构。而我们先设计一维折叠式S型周期振子，再将振子周期贴附在双层梁表面，相当于声子晶体中嵌套声子晶体。

从图8(a)中可以看到，能带结构没有明显的带隙，然而其对应的振动传输曲线却存在很宽的衰减频域，且范围大致与S型振子的衰减频域范围相对应。为了发现其中的带隙特性，揭示其展示出来的现象，作出了相应衰减频域的位移场，如图10所示。

图10 与图8(a)中标注的特征模态相对应的位移场Fig.10 The displacement fields of eigenmodes labeled in Fig.8(a)

由图10可以看到，在衰减频域内，无论这几种模态中位移场下(上)层板如何振动，上(下)层板都保持静止，这表明一个板的振动不会传到另外一个板上，进而说明该结构在相应的频域内有良好的隔振性能。之所以能带结构都没有明显的带隙，而其对应的振动传输曲线却存在很宽的衰减频域且结构存在良好的隔振性能。是因为在衰减频域内，频率落在中间振子的带隙频段内，此结构中间的S型振子起到了关键的隔振作用，因此才会出现这种现象。在图10中，模态F1，F2主要为沿z方向的垂直振动，与板中z方向振动的弯曲弹性波相互耦合，形成弯曲弹性波共振带隙。对于模态F3和F4，位移场为上板绕水平面内中轴线旋转振动的模态与双层板垂直板面弯曲振动的模态相互耦合的结果。对于模态F5，位移场为下板作沿板方向的纵向振动，上板和中间振子基本保持静止。对于模态F6，位移场为两个周期的S型振子产生振动，上下板基本保持静止。这是因为模态F6是能带结构图中临界点的特征模态相对应的位移场，所以中间振子最上方开始存在小幅度的振动，这也刚好符合单层梁结构中对应的D6模态的位移场。其中，这6个模态中，F1～F5都是振动能量集中在一侧板，而中间振子和另一侧板基本保持静止。对于模态F6，这个模态处于振子能带结构图临界点，所以中间振子最上方开始存在小幅度的振动，但振动还是不能从一侧板传递到另一侧板。

为了进一步说明该衰减特性，给出了频率落在衰减域的有限声子晶体双层梁结构的振型图，如图11(a)所示。这里，计算所用到的模型如图9所示，激励点施加纵向的位移激励并且频率点选为f=60 Hz。由图11(a)可以看出，当激励施加于下板时，振动无法通过上层板传播，而仅仅可以通过下层板传播。总的来说，当振源和响应域分别在双层梁结构的异侧时，可以被认为是一条在相应有限结构中振动衰减的带隙被打开。而频率落在非衰减域的有限双层梁结构的振型图，如图11(b)所示，频率点选为f=27 Hz。可以看出，当激励施加于下板时，振动能很好的传递到上层板。

图11 频率落在不同区域的有限声子晶体双层梁结构的振型图Fig.11 Mode diagrams of finite phononic crystal double-layer beam structures with frequencies falling in different regions

2.4 各参数对声子晶体梁结构带隙衰减频段的影响规律

计算用到的参数与图8(a)所示的参数一致，具体如表1和表2所示。铅层厚度h3、上下板厚度e、晶格常数a、振子宽度m以及橡胶层厚度h1被选取为影响参数，用来研究几何参数对带隙衰减频段的起始频率、终止频率和带隙衰减宽度的影响规律。

对于局域共振型声子晶体梁结构，由图12(a)可以看到，随着振子宽度的增大，带隙衰减频段的起始频率略微升高，而终止频率较大程度下降，此消彼长，带隙宽度有较大的减少。由图12(b)可以看到，晶格常数对带隙衰减频段和带隙宽度影响不大，带隙衰减频段的起始频率基本不变，终止频率有微小的提升，而带隙宽度变化不大。而随着铅层厚度的增大，带隙衰减频段的起始频率和终止频率均减小，带隙宽度有一定程度的降低，如图12(c)所示。带隙衰减频段和带隙宽度与上下板厚度之间的关系，如图12(d)所示。随着上下板厚度的增大，带隙衰减频段的起始频率基本不变，终止频率微小的提升，因此带隙宽度有十分微小的幅度增大。由图12(e)可以看到，随着橡胶层厚度的增大，带隙衰减频段的起始频率和终止频率均减小，而终止频率减小的幅度更大，因此带隙宽度也较小幅度降低。

图12 各参数对声子晶体梁结构带隙衰减频段的影响规律Fig.12 The influence of various parameters on band gap attenuation frequency of phononic crystal beam structure

3 结 论

针对工程中的振动噪声控制问题，提出了一种声子晶体梁结构，采用有限元法计算了该结构能带结构、特征模态所对应的位移场以及相应有限周期双层梁结构的振动传输曲线，对其展现出的带隙特性进行了研究。对比分析了声子晶体单层梁结构和声子晶体双层梁结构的带隙特性，研究了单/双层梁振动的通性。并研究了各参数对声子晶体双层梁结构带隙衰减频段的影响规律。结论概括为：

(1)通过对能带结构和传输曲线进行分析，一条低频率低并且带隙较宽的带隙可以被打开。对带隙边界能带的特征模态相对应的位移场进行分析，带隙的打开可以认为是中间振子的振动模态和上下板的板振动模态相互耦合作用的结果。此结构与对应的S型振子衰减频域大致相同，且此结构由于中间S型振子的作用，在相应频域内对双层梁结构有良好的隔振性能。

(2)对比分析了声子晶体单层梁结构和声子晶体双层梁结构的带隙特性，研究了单/双层梁结构振动的通性。对于声子晶体双层梁结构，在特定频率的减振降噪有良好的作用，而声子晶体梁单层梁结构效果甚微。

(3)研究各参数对声子晶体梁结构带隙衰减频段的影响规律，可以归纳为：①通过增加振子宽度，可以提高带隙起始频率，降低终止频率从而导致带隙宽度减少；②晶格常数和上下板厚度对带隙起始频率，终止频率和带隙宽度影响不大；③通过增加橡胶层和铅层厚度，带隙起始频率，终止频率和带隙宽度均降低，且带隙宽度降低幅度相差不大。