参数优化最大二阶循环平稳盲解卷积行星轮轴承故障提取

林 云， 郭 瑜， 陈 鑫

(昆明理工大学 机电工程学院，昆明 650500)

行星齿轮箱广泛用于风力发电、直升机、工程机械等大型复杂机械装备中，其恶劣的工作环境导致其易产生故障。行星轮轴承是行星齿轮箱中较容易产生故障的零部件，因此研究行星轮轴承故障特征提取方法对机械设备的安全运行具有重要意义。

滚动轴承故障源信号的传递过程可以看作是源信号与信道的一个线性卷积混合过程[1]，因此可以通过解卷积运算恢复故障冲击脉冲。相关解卷积算法中，Mcdonald等[2]最近提出的多点优最小熵反卷积(multipoint optimal minimum entropy deconvolution adjusted, MOMEDA)算法，在滚动轴承故障特征提取上取得较好效果[3]，但Buzzoni等[4]使用的周期准则与轴承故障冲击的循环平稳性不符，在强噪声干扰下，算法可能会失效。近期，Buzzoni等提出最大二阶循环平稳盲解卷积(maximum second order cyclostationary blind deconvolution，CYCBD)算法。算法利用了二阶循环平稳指标(second order indicators of cyclostationary，ICS2)对故障冲击敏感的特性，具有较好的鲁棒性。近年来，针对滚动轴承故障诊断的研究表明，该算法可以有效提取轴承故障冲击，且相对于Momeda等的算法更具优势[5]。但在轴承滑移条件下，利用CYCBD技术提取行星轮轴承故障特征，算法中循环频率和滤波器长度的准确选取仍是一个难点。

近期，罗忠等[6]提出了故障特征比(fault feature ratio，FFR)指标，其旨在反映包络谱中的故障特征频率及其谐波的显著程度，但尚存在如下问题：①未考虑轴承滑移的情况；②指标中谐波均值较大时，不一定反映了各个谐波均显著；③指标所选的频率范围受到干扰较大。为此，本文研究中提出一种改进故障特征比(improved fault feature ratio，IFFR)指标，以该指标作为粒子群算法的适应度函数自动获取CYCBD算法中循环频率和滤波器长度。通过行星轮轴承外圈故障特征提取的仿真和试验对比分析，结果反映了本文方法的有效性和优势。

1 基于改进FFR指标的适应度函数

在利用智能算法优化参数时，适应度函数决定了整个优化过程的方向和目标，而建立合适的适应度函数是此类问题的重点和难点。近期，罗忠等提出了FFR指标作为粒子群算法的适应度函数。该指标通过计算包络谱中故障特征频率分量所占比重来反映故障特征提取效果，表达式如下

(1)

ASi=max[AS(ifm-0.02fm,ifm+0.02fm)]

(2)

式中:ASi为包络谱中第i阶故障特征频率处的幅值；I为选取的故障谐波数；ASt为包络谱中1～1 000 Hz频率幅值之和；E(·)为求均值；fm为故障特征频率。

尽管该指标能够一定程度反映故障特征提取效果，但仍存在以下不足：①在式(1)分子中，指标通过故障各阶谐波的均值来反映故障特征显著程度，而当包络谱中某一阶故障特征频率明显突出时，即使其他谐波处幅值即使并不显著，也会使该均值较大，此时FFR指标将主要反映单个谐波的显著程度；②式(2)中对每一阶谐波附近进行峰值搜索的范围均为理论故障频率的±2%内，当轴承在运行过程中存在一定滑移时，在较高阶的谐波处，实际故障特征频率将可能超出该峰值搜索范围，导致指标失效；③平方包络谱开始的前几赫兹频率有可能出现一些大峰值的影响[7]，因此，固定地弃掉前1 Hz频率成分难以有效消除平方包络谱具有较大幅值的低频干扰。限制了该指标在平方包络谱中的应用。

为解决上述问题，研究中提出IFFR指标，其表达式为

IIFFR(i)=min[Mi/E(MSES)],i=1,…,N

(3)

Mi=max{M[ifω(1-0.02),ifω(1+0.02)]}

(4)

MSES=[M(fω-0.5fω,Nfω+0.5fω)]

(5)

式中:M(·)为取信号幅值；i为包络谱中第i阶故障谐波；N为所取的故障谐波总数；E(·)为求均值；fω为故障特征频率。

IFFR指标选取了信号前i阶故障谐波中故障特征比的最小值，从而保证了当该指标越大，前i阶故障谐波越显著；第i阶理论故障谐波处的峰值搜索范围相应扩大为第一阶理论故障谐波的i倍，保证了滑移条件下，实际故障特征频率及其谐波不会超出搜索范围；该指标在求包络谱均值时选取式(5)中较窄的频率范围，避免了其他频率范围的影响。

行星轮轴承外圈故障仿真和试验信号处理结果表明，该指标能够较好地揭示包络谱中各阶谐波的显著程度，进而保障故障特征提取的准确性和效果。

2 参数优化CYCBD算法

2.1 CYCBD算法原理

CYCBD算法是一种基于广义瑞利熵和循环平稳指标的新型盲解卷积算法，可以用于提取具有循环平稳特性的故障冲击信号。在解卷积算法模型中，一般通过测量信号x来估计目标输入信号s0，此类算法的基本原理可以用式(6)表示

s=x*h≈s0

(6)

式中:s为估计源信号；h为逆滤波器；*为卷积运算。式(6)的矩阵形式为

s=Xh

(7)

(8)

式中:L为离散信号s的点数；N为逆滤波器h的长度。

在广义瑞利熵的框架下，求解最大ICS2值被转化为求解广义瑞利熵的特征值，此时ICS2可定义为

(9)

式中，RXWX和RXX分别为加权相关矩阵和相关矩阵。加权矩阵W可以表示为

(10)

E=(e1…ek…ek)

(12)

(13)

式中:k为循环频率集的大小；Ts为故障冲击周期。由于循环频率被认为是与信号能量波动相关的频率，可与轴承故障或齿轮故障等相关，因此可将离散信号的循环频率定义为k/Ts[8]，而离散信号的理论故障频率为1/Ts，因此可基于理论故障频率计算循环频率。

需要说明的是，CYCBD算法目的在于求解最佳逆滤波器，而获取加权矩阵W是其核心的步骤。在计算W时，需要提供滤波器长度和循环频率这两个参数，其设置准确与否对最终求得的逆滤波器会产生较大影响。

2.2 参数优化CYCBD

粒子群算法[9]是一种仿生优化模型，该算法具备较好的全局优化性能。其原理简述如下：①在D维空间中，N个粒子组成一个种群，则第m个粒子为一个D维向量，粒子的位置和速度分别为Xm=(xm1,xm2,…,xmD)，Vm=(vm1,vm2,…,vmD)，其中，m=1,2,…,N；②第m个粒子搜索到的最优位置和整个粒子群搜索到的最优位置可分别记为Pbest=(pm1,pm2, …,pmD),gbest=(g1,g2, …,gD),其中，m=1,2,…,N;③各个粒子可分别根据式(14)和式(15)来更新自己的速度和位置

vmn(t+1)=λ·vmn(t)+c1r1(t)[pmn(t)-xmn(t)]+

c2r2(t)[pgn(t)-xmn(t)]

(14)

xmn(t+1)=xmn(t)+vmn(t+1)

(15)

式中:c1,c2为学习因子,分别为个体经验和社会经验对粒子运动路线的影响；r1,r2为0～1的随机数；λ为惯性权重, 惯性权重的大小表示粒子下一步速度对当前速度继承量的百分比。

通过合理设置各项参数，可以使粒子快速而准确到达目标位置，完成参数优化过程。在式(14)中学习因子c1和c2按照文献[10]设置为c1=c2=1.5；惯性权重设置在0.9～1.2时，算法具有比较好的搜索性能[11]，本文设置为λmax=1.2，λmin=0.9。

3 故障特征提取流程

本文提出一种基于参数优化最大二阶循环平稳盲解卷积的行星轮轴承故障特征提取方法，其实现基本步骤为：

步骤1利用键相脉冲信号将原始时域信号通过阶比分析技术转换为角域信号，消除转速波动干扰；

步骤2利用离散随机分离(discrete random separation，DRS)[12]技术将齿轮相关信号和轴承信号进行分离，抑制齿轮相关信号的影响；

步骤3利用CYCBD技术对轴承信号部分进一步处理，在CYCBD算法中，基于理论故障特征阶次确定循环频率搜索范围，基于理论故障周期点数确定滤波器长度搜索范围，粒子的位置坐标由循环频率和滤波器长度两个参数构成，根据参数搜索范围和搜索精度，设定种群大小N和最大迭代次数I；

步骤4设置适应度函数为IFFR，初始化CYCBD参数，其中迭代步数设置为5，迭代精度为10-4；

步骤5计算种群中N个个体的适应度值，记录最大的适应度值，记录此时粒子的位置；

步骤6更新种群位置，求种群N个个体的适应度值，记录此轮迭代最大适应度值，与当前最大适应度值进行对比，取其大者，更新最大适应度值；

步骤7重复步骤5和步骤6，直到达到最大迭代次数I，输出最大适应度值及其对应的位置坐标；

步骤8根据位置坐标得到的循环频率和滤波器长度作为CYCBD的优化输入参数，算法中循环频率集大小取为k=100。求解卷积信号的平方包络谱，提取故障特征。

该方法的流程如图1所示。

图1 基于参数优化最大二阶循环平稳盲解卷积的行星轮轴承故障提取方法Fig.1 Fault extraction method of planet bearing based on parameter optimized CYCBD

4 仿真验证

4.1 仿真信号构造

滚动轴承的局部故障振动仿真信号，可用式(16)～式(18)表示[13]

(16)

Ai=Aocos(2πQt+φA)+CA

(17)

s(t)=e-βtsin(2πfnt+φw)

(18)

式中:Ai为信号幅值调制部分；M为故障冲击脉冲个数；T为故障冲击时间间隔；τi为滚动轴承随机滑移；fn为系统的固有频率；Q为轴承转频；φw和φA为初始相位；n(t)为高斯白噪声。

仿真的行星轮轴承外圈局部故障振动信号主要包括：齿轮信号、轴承信号和噪声信号三部分。

(1)轴承信号。与单一滚动轴承故障不同的是，行星轮轴承发生局部故障时，轴承信号具有更为复杂的调制。由于行星传动结构，行星轮轴承外圈既有自转又有公转。其中，自转与行星轮绕行星轮轴的旋转有关，二者转频相同，在故障振动信号中表现为行星轮的转频调制现象。整个行星轮轴承会随行星架一起旋转，产生时变路径效应，在故障振动信号中表现为与行星架转频相关的调幅作用。对于传感器安装于齿圈上方的情况，时变路径调幅效应可以用Hanning窗函数来表示[14]。基于上述分析，行星轮轴承外圈局部故障仿真，轴承信号部分可用式(19)和式(20)表示

[1-cos(2πfct)]×s(t-iTP-τi)(19)

s(t)=e-βtsin(2πfn1t+φw)

(20)

式中:Ai为第i个故障冲击的幅值；fp为行星轮的旋转频率；fc为行星架旋转频率；τi为轴承滑移，在0～0.02TP随机取值；fn1为轴承固有频率；β为阻尼比。

(2)齿轮信号。行星齿轮箱在运转过程中，齿轮啮合包括行星轮分别和太阳轮、齿圈的啮合。齿轮轮齿啮合同样会激起共振，且轮齿啮合引起的共振大于故障轴承[15]。齿轮信号部分可表示为

(21)

式中:Aj为第j次轮齿啮合的幅值；N为齿轮啮合次数；TQ为齿轮信号的啮合周期；fn2为齿轮固有频率。

(3)噪声信号。考虑噪声影响，在仿真信号中加入信噪比为-10 dB的高斯白噪声。

行星轮轴承外圈故障仿真信号可用式(22)表示

x(t)=xout,bearing(t)+xgear(t)+xnoise(t)

(22)

式中，xnoise(t)为高斯白噪声。

仿真信号的具体参数如表1所示。

表1 行星轮轴承外圈故障仿真参数Tab.1 Simulation parameters of planetary gear bearing with fault on outer race

行星轮轴承故障冲击周期可由式(23)计算

(23)

式中，fbo为行星轮轴承外圈故障特征频率。

4.2 故障特征提取

仿真信号原始时域信号如图2所示，其频谱如图3所示，图中轮齿啮合频率及其谐波较为显著，而行星轮轴承外圈故障特征频率fbo(100 Hz)被噪声淹没。

图2 时域信号Fig.2 Time domain signal

图3 信号频谱Fig.3 Spectrum of signal

原始信号中，齿轮信号等强周期信号的干扰较大，难以直接提取行星轮轴承故障冲击特征。因此，先用DRS技术对原始时域信号进行信号分离，得到周期信号部分和随机信号部分，其中随机信号部分包含了轴承故障冲击信号，用该部分作为CYCBD算法的输入信号。

由表1可知，行星轮轴承外圈理论故障特征频率为fbo=100 Hz，考虑轴承存在约2%以内的滑移[16]，粒子群算法中故障循环频率的搜索区间设置为：[98,102]；而最小滤波器长度要能覆盖轴承故障所产生的冲击信号衰减周期且最大长度不宜过大，本文设置滤波器长度的搜索范围为0.5Tbo～1.5Tbo，即[120,360]。此外，循环频率搜索区间长度(按循环频率的搜索精度为0.1 Hz计算)为40，按照黄包裕等设置种群大小为区间长度的1/2，设置迭代次数I=10。

首先利用基于FFR指标的粒子群算法优化CYCBD参数，指标中谐波总数N取为4。在粒子群算法中，循环频率搜索速度范围设置为[-0.02,0.02]；滤波器长度搜索速度范围设置为[-10,10]。算法的迭代图如图4(a)所示，图中可见第6次迭代时，FFR指标值达到最大。对应的优化循环频率和滤波器长度分别为99.6 Hz和296。将此参数应用于CYCBD算法，解卷积结果如图4(b)所示。从图4(b)中可见，相对于图2所示的原始故障信号，故障冲击一定程度被增强。结果的平方包络阶比谱如图4(c)所示，该指标指示的平方包络谱中，故障特征频率的二阶谐波较为显著，而故障特征频率处被噪声淹没，说明FFR指标存在主要反映单个谐波显著程度的情况，不利于故障特征的有效提取。

图4 基于FFR指标的CYCBD算法处理仿真信号Fig.4 FFR index based CYCBD algorithm to process simulation signal

随后，采用本文所提出的基于IFFR指标的粒子群算法优化CYCBD参数。图5(a)所示为利用基于IFFR指标的粒子群算法优化CYCBD参数过程的迭代图，图中可见在第7轮迭代时，优化值达到最大，此时对应的优化循环频率和滤波器长度分别为99.1 Hz和342。将此参数应用于CYCBD算法，解卷积结果如图5(b)所示。相对于图4(b)所示的解卷积结果，故障冲击增强效果更好。结果的平方包络谱如图5(c)所示。图中故障特征阶次及其谐波较为明显的反映出了行星轮轴承外圈故障特征，表明利用IFFR指标能够较好地反映平方包络谱中的故障显著程度。

图5 基于IFFR指标的CYCBD算法处理仿真信号Fig.5 IFFR index based CYCBD algorithm to process simulation signal

相对于图4(c)，图5(c)能够更好地反映行星轮轴承外圈故障特征，而计算图5(c)所示结果的FFR值仅为0.31，小于图4(c)结果的FFR值(2.33)。可知在获取CYCBD算法优化参数组合时，利用IFFR指标作为适应度函数，其效果要优于相同条件下的FFR指标。

5 试验验证

5.1 试验数据采集

利用行星齿轮箱综合试验台进行试验，以NGW型单级行星齿轮箱为试验对象，采集行星轮轴承故障振动数据，输入转速设置为1 000 r/min。对本文所提方法进行验证。加速度传感器和电涡流传感器的安装位置如图6所示，分别用于拾取振动信号和同步转速脉冲。其中加速度传感器为RION PV-86 4527型；电涡流传感器为DH90型。通过齿圈传递到箱体正上方的信号传递路径最短，可以得到信噪比相对较高的信号，试验中在该处拾取振动信号。此外，信号采集系统中使用NI USB9234型采集卡和DH-5853型电荷放大器，采样频率为51.2 kHz，信号放大倍数为3。

图6 传感器安装位置Fig.6 Location of sensor installation

齿轮箱内行星轮轴承、齿轮参数分别如表2、表3 所示。由相关故障理论，利用表2和表3数据计算得到行星轮轴承外圈故障相关频率如表4所示。

表2 行星轮轴承参数Tab.2 Parameters of planet bearing

表3 齿轮参数Tab.3 Parameters of gears

表4 行星轮轴承外圈故障相关频率Tab.4 Frequencies related to the planet bearing with faulty outer race 单位：Hz

研究中，选择输出轴(对应行星架转轴)作为参考轴，即其阶次为1，其他相关元件可利用对应信号频率值按式(24)计算阶次

(24)

式中:l为阶次；f为信号频率；n为参考轴转速。

由式(24)可计算得到行星轮轴承外圈故障相关阶次如表5所示。

表5 行星轮轴承外圈故障相关阶次Tab.5 Orders related to the planet bearing with faulty outer race

图7所示为轴承故障为电火花加工的人造局部故障，故障宽度约为1 mm，深度约为0.5 mm。

图7 行星轮轴承外圈人造局部故障Fig.7 Artificial local fault of outer race of planet bearing

5.2 故障特征提取

为消除转速波动的影响，以行星架转轴为参考，将原始时域振动信号转换到角域。设置等角度重采样率设置为Fs=9 088 r/min，为齿圈齿数的128倍。原始角域信号如图8所示，其包络阶比谱如图9所示。从图9中可见，各部件转频成分及其谐波较为显著，而行星轮轴承外圈故障特征阶次lbo(9.57)几乎被噪声淹没。

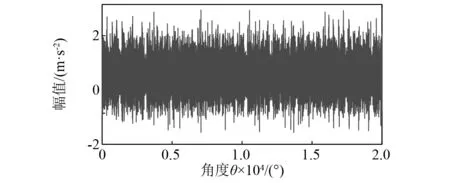
图8 角域信号Fig.8 Angular domain signal

图9 角域信号包络阶比谱Fig.9 Envelope order spectrum of angular domain signal

利用DRS技术对原始角域信号进行信号分离，分离得到的随机信号部分进行后续的参数自适应CYCBD算法处理。考虑到算法计算效率，对DRS分离后的随机信号部分进行降采样，重采样频率Fs=4 544点/转。由表5可知，行星轮轴承外圈理论故障阶次为lbo=9.57，根据上文中关于理论故障频率与循环频率的关系，对应循环频率的搜索区间设置为：[9.37,9.76], 区间长度(按循环频率的搜索精度为0.01阶计算)为40；由式(23)计算得，Tbo=474.8点，设置滤波器长度的搜索范围为0.5Tbo～1.5Tbo，即[237,713]。设置种群大小为区间长度的1/2，设置迭代次数I=10。

首先利用基于FFR指标的粒子群算法优化CYCBD参数，指标中谐波总数N取为4。在粒子群算法中，循环频率搜索速度范围设置为[-0.02,0.02]；滤波器长度搜索速度范围设置为[-10,10]。算法的迭代图如图10(a)所示，图中可见第7次迭代时，FFR指标值达到最大。对应的优化循环频率(阶次)和滤波器长度分别为9.66和395。将此参数应用于CYCBD算法，解卷积结果如图10(b)所示，对比图8原始角域信号，图10(b)中难以观察到故障特征增强效果。结果的平方包络阶比谱如图10(c)所示，图中虚线指示为故障特征阶次及其谐波位置，该指标指示的平方包络谱中，难以观察到故障特征。

图10 基于FFR指标的CYCBD算法处理试验信号Fig.10 FFR index based CYCBD algorithm to process experimental signal

随后，采用本文所提出的方法。图11(a)所示为利用基于IFFR指标的粒子群算法优化CYCBD参数过程的迭代图，图中可见在第6轮迭代时，优化值达到最大，此时对应的优化循环频率(阶次)和滤波器长度分别为9.42和714。将此参数应用于CYCBD算法，解卷积结果如图11(b)所示。相对于图10(b)所示的解卷积结果，故障冲击增强效果更为明显。结果的平方包络谱如图11(c)所示。图中行星轮轴承外圈故障特征阶次及其谐波较为显著。表明基于IFFR指标的粒子群算法能够有效的获取CYCBD算法中较佳的参数组合，进而利用参数优化的CYCBD算法可以准确提取行星轮轴承外圈故障特征。需要说明的是，试验信号由于轴承滑移现象，行星轮轴承外圈实际故障阶次与理论故障阶次(9.57)存在约1.6%的误差。

图11 基于IFFR指标的CYCBD算法处理试验信号Fig.11 IFFR index based CYCBD algorithm to process experimental signal

相对于图10(c)结果，图11(c)结果能够更好地反映行星轮轴承外圈故障特征，而计算图11(c)所示结果的FFR值仅为3.50，小于图10(c)结果的FFR值(5.70)。可见在获取CYCBD算法优化参数组合时，利用IFFR指标作为适应度函数，其效果要优于相同条件下的FFR指标。

6 结 论

本文针对现有CYCBD算法FFR指标存在的问题，提出一种基于参数优化最大二阶循环平稳盲解卷积的行星轮轴承故障提取方法。对原FFR指标进行了改进，提出了IFFR指标。将IFFR作为粒子群算法的适应度函数对CYCBD算法的循环频率和滤波器长度进行优化选取可以取得较好的效果。通过行星轮轴承外圈故障仿真和试验验证了方法的有效性和优势。