关于薄壁曲梁与直梁解析解的进一步讨论1)
赵迎港 杨宇威 赵颖涛 高 阳 王敏中
*(北京理工大学宇航学院,北京 100081)
†(中国农业大学理学院,北京 100083)
**(北京大学工学院,北京 100871)
平面问题是反映弹性力学求解思想的一类典型问题,其求解通常可以转化为Airy应力函数的求解问题。解决此类问题通常采用半逆解法,即首先假设Airy应力函数的形式,再根据边界条件求解Airy应力函数的精确表达,从而得到区域内的应力场和应变场。
对于研究薄壁曲梁与直梁(即矩形横截面的宽度b远小于高度h,如图1(a)所示)的平面应力问题,两类问题Ariy应力函数的假设形式以及边界条件的提法都有很多的相似之处,其解也具有相似性。从图1可以看出,直梁的应力分量σx(图1(b))和曲梁的应力分量σθ(图1(c))的分布几乎完全相同。

图1 纯弯曲情形下的直梁和曲梁的应力
对于有限尺寸(高度h有限)的薄壁曲梁,当其曲率半径和横截面尺寸之比趋于无穷时,则其几何特征将会无限逼近于直梁,理论上其应力结果也会无限逼近于直梁受力的结果。本文从薄壁曲梁弯曲问题的解析解出发,通过对曲梁曲率半径和其横截面高度之比取极限,最后推导出直梁弯曲的结果,不仅可以说明两个问题在应力函数假设以及边界条件处理上的相似性,也可以帮助读者理解直和曲的辩证统一关系。
1 薄壁曲梁和直梁问题的提法
本文研究了薄壁曲梁与直梁受到弯矩M、剪切力Q、拉力P的作用时,其应力分布之间的关系,其中直梁与曲梁的几何构型及受力状况如图2所示。

图2 曲梁与直梁受力示意图
那么,曲梁(极坐标系下)和直梁(直角坐标系下)问题的完整提法可分别写为

其中U为Airy应力函数。显然二者的提法完全相似,其结果也应该具有一定的相关性。
为了方便研究二者的关系,假设曲梁中线的长度L与曲梁的横截面尺寸(高度)h不发生变化。当曲梁中线的曲率半径和梁的高度之比趋于无穷,即R/h→∞时,曲梁的几何特征将会无限趋近于直梁(如图3所示),曲梁的受力问题也应无限趋近于直梁。下面对这两种杆件在特定载荷作用下的解析解分别进行讨论。为了方便推导,本文有时也会用曲梁的内径或外径与梁的高度之比趋于无穷来描述该极限过程,即用a/h→∞或b/h→∞代替R/h→∞。
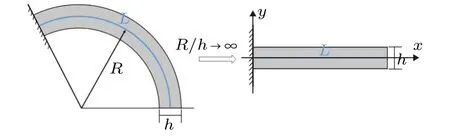
图3 极限过程示意图
2 曲杆和直杆在特定载荷下的解析解对比
2.1 纯弯曲情形( P =Q=0,M/=0 )
如图2(a)所示,仅有力偶矩M时,可以得到薄壁曲梁的应力场和位移场分别为[1-2]
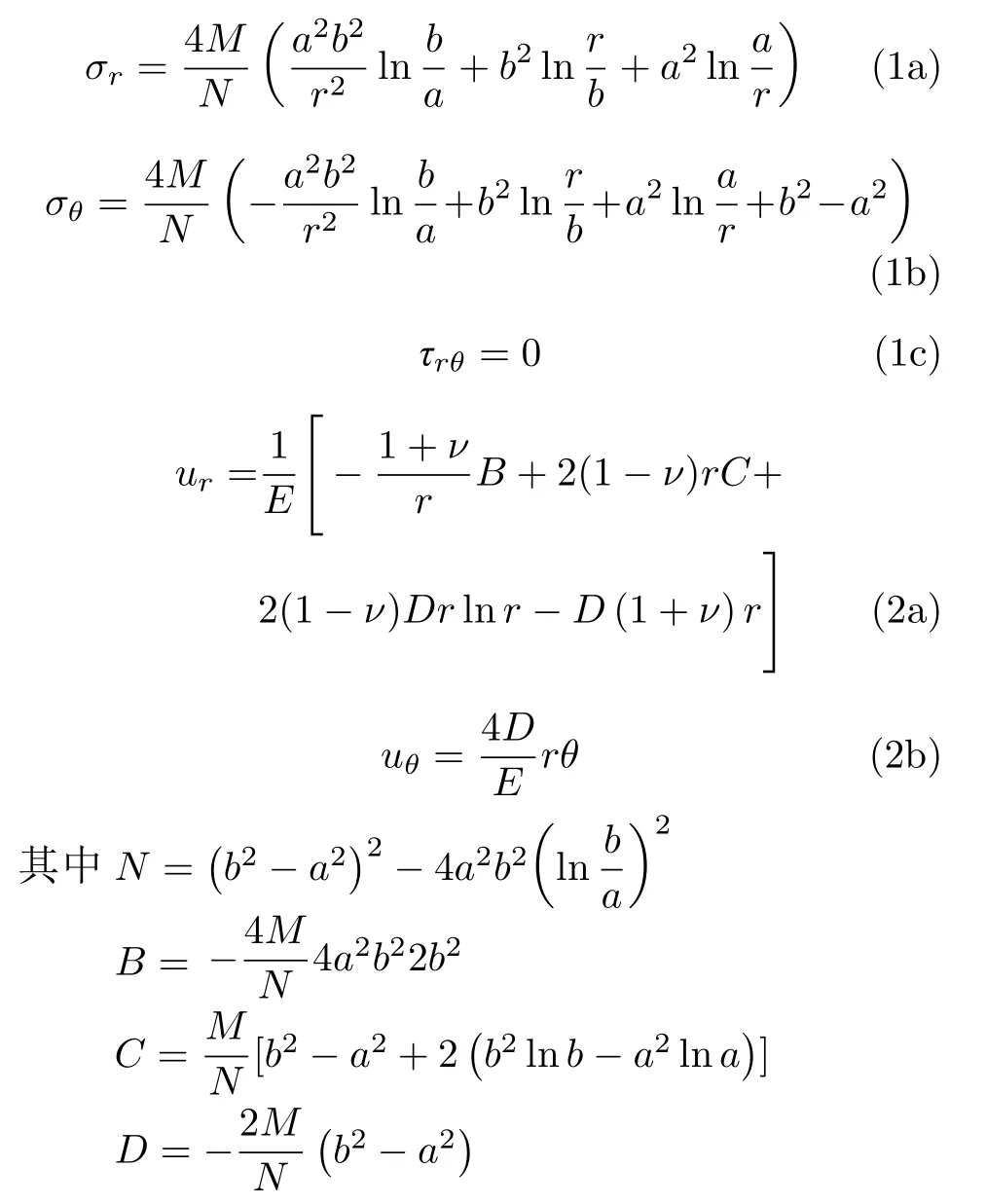
对曲梁的曲率半径(外径、内径)取极限,各参量的关系为
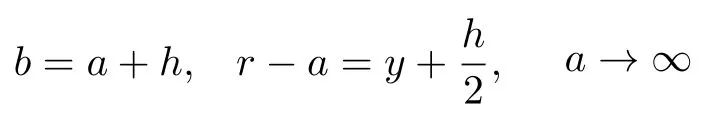
首先对分母N进行计算有

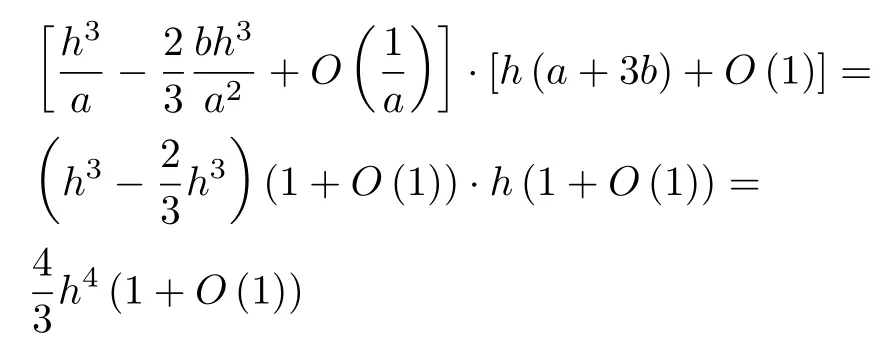
然后对正应力σr取极限,为了方便计算,记
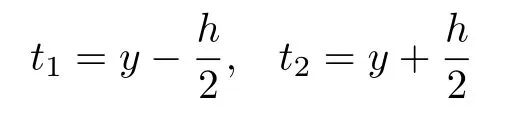
则式(1a)括号内的项可化简为
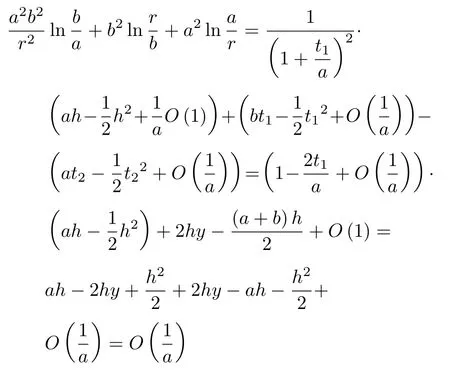
当a→ ∞时,正应力σr可化为
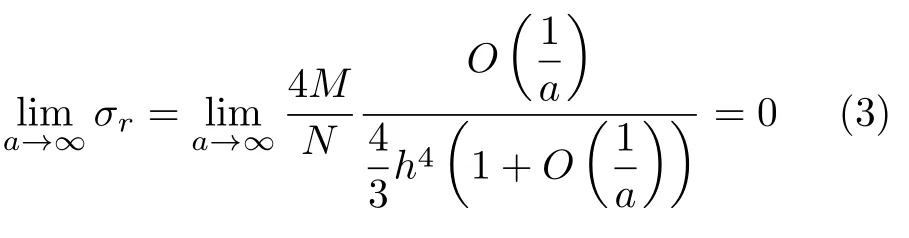
同样,可以计算正应力σθ在a→ ∞时的极限。首先对式(1b)括号内的项化简可得
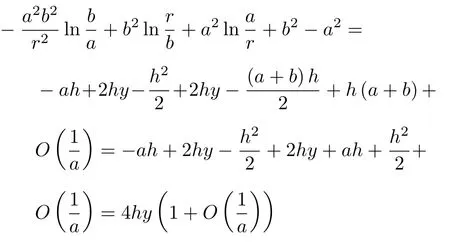
那么
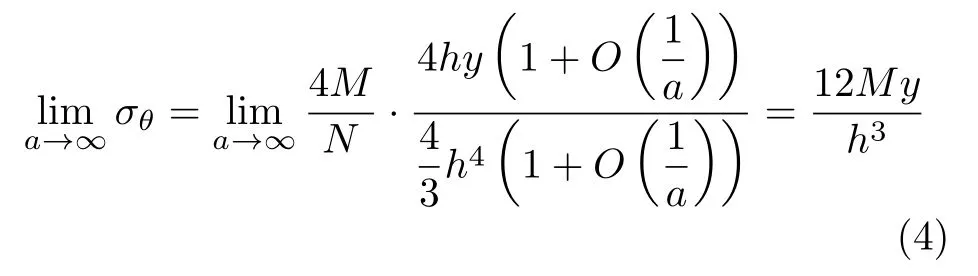
综合式(1c)、式(3)和式(4)可知,当a→∞,纯弯曲作用下薄壁曲梁的应力场σr,σθ,τrθ分别退化为

此即为薄壁直梁纯弯曲时应力场的解
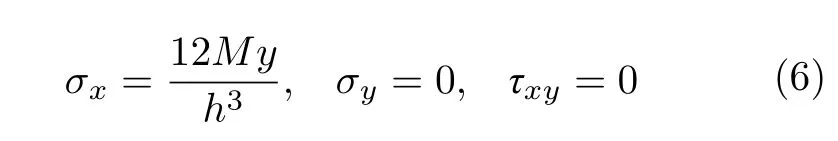
下面讨论位移场和中性轴的特征。
由式(2b)可以看出,曲梁任一截面的位移相当于绕曲率中心转动了一个角度。也就是说曲梁在纯弯曲状态下和直梁一致,也满足平截面假设[2]。
记曲梁的中性轴方程为r=r0,由方程(1b)可知中性轴满足方程
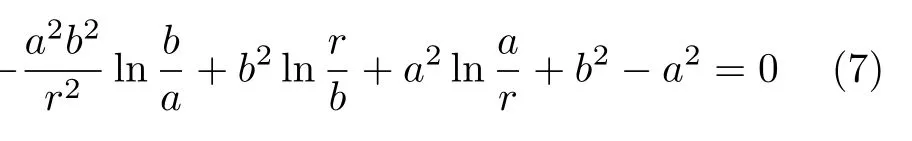
此方程为超越方程,无解析解,我们可以通过数值方法对其求解。定义R/h为曲梁的相对曲率半径,其中R=(a+b)/2 为曲梁的中轴线半径,根据式(7)的解可以画出中性轴的相对位置 (r0-a)/h随R/h的变化关系,如图4所示。从图中可看出,当相对曲率半径增大时,中性轴的位置也由靠近内径的一侧向曲梁中线靠近,当R/h→∞时,曲梁也退化为直梁,中性轴的位置趋近于直梁的轴线,也就是 (r0-a)/h→0.5 。

图4 曲梁中性轴位置的变化趋势
由薄壁曲梁和直梁的应力场、位移场和中性轴的对比分析可知,在纯弯曲情形下,薄壁直梁可视为薄壁曲梁在曲率半径趋于无限大时的特殊情形。
2.2 剪力情形( P =0,Q/=0,M=0 )
当仅有切向力Q时,可以得到薄壁曲梁的应力场为[1-2]

同上,对曲梁的曲率半径(外径、内径)取极限,各参量的关系如下所示
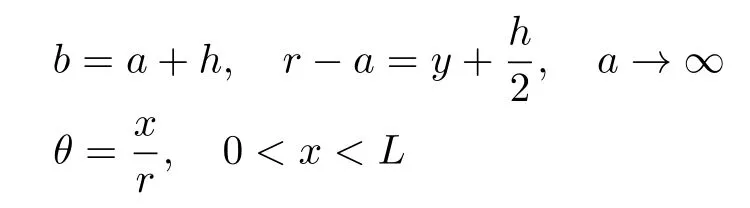
相似的计算可得

而式(8a)的部分项可化简为
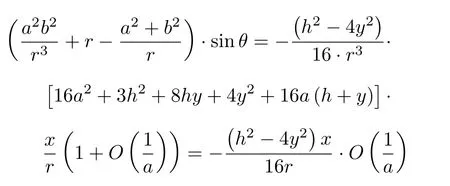
当a→ ∞时,正应力σr可化为

同样,考察正应力σθ在a→ ∞时的极限。对式(8b)中的部分项化简可得 Å ã


那么

最后考察剪应力τrθ。式(8c)中的部分项可化简为

取极限可得

综合式(9)~式(11)可知,当a→∞,仅有剪力Q弯曲作用下薄壁曲梁的应力场σr,σθ,τrθ分别退化为
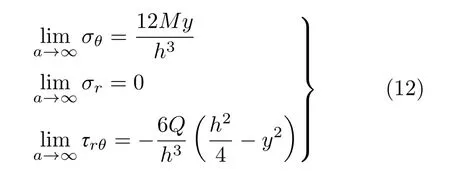
此即为薄壁直梁在剪力Q作用下的解

也就是说,仅有剪力Q作用下,薄壁直梁亦可视为薄壁曲梁在曲率半径趋于无穷大时的特殊情形。
2.3 仅有法向力P的情形( P /=0,Q=0,M=0 )
当仅有法向力P时,可以得到薄壁曲梁的应力场为[1-2]

对曲梁的曲率半径(外径、内径)取极限,各参量的关系如下所示

参照2.2节剪应力的结果,可以得出

考虑r方向应力的第一部分有

第二部分

综合式(14a)、式(17)和式(18),可以得到

而后,考虑θ方向上应力的第一部分

第二部分

结合式(20)和式(21),可得

也即,在仅有拉伸作用P的情况下,薄壁曲梁的解退化为

这与直杆单向拉伸的结果一致。
3 结论
本文对薄壁曲梁与直梁端部受力问题进行了对比分析,结果表明,曲梁弯曲的解析解在曲率半径与横截面尺寸之比趋于无穷时,可以退化为直梁受力弯曲的解析解,这也说明薄壁直梁的受力问题可视为薄壁曲梁在曲率半径趋于无限大时的退化情形。这不仅可以帮助读者更好地理解弹性力学平面问题中极坐标解法和直角坐标解法的内在联系,也从侧面说明了曲和直之间的辩证关系。同时,本文的讨论也可以给我们更多启示,即对于区域边界为圆或者圆弧的力学问题,其结果在曲率半径趋于无穷的时候,应当可以退化为平直边界的情形。

