随机及移动荷载激励下弹性梁分岔与混沌*

李海涛秦卫阳†田瑞兰

（1.西北工业大学工程力学系，西安 710072）（2.石家庄铁道大学数理系，石家庄 050043）

随机及移动荷载激励下弹性梁分岔与混沌*

李海涛1秦卫阳1†田瑞兰2

（1.西北工业大学工程力学系，西安 710072）（2.石家庄铁道大学数理系，石家庄 050043）

移动荷载通过简支梁时，粗糙的梁表面会使移动荷载转变为随机激励.本文考虑梁的几何非线性因素，基于随机Melnikov理论确定了系统在均方意义下发生异宿分岔以及混沌的边界条件.利用数值随机Runge-Kutta方法对随机激励和周期激励共同作用下的系统响应进行了仿真计算，最大Lyapunov指数等数值结果描述了动力学行为变化过程.结果表明当荷载的速度一定时，梁跨中的非线性动力学行为受到质量和随机激励的共同影响，表面平整度较差的梁会增加混沌产生的可能性.

表面平整度，移动荷载，随机Melnikov过程，混沌

引言

移动荷载是车辆荷载和重物荷载的简化模型，可以广泛应用到“车-桥”系统和“龙门吊”起重机等系统的研究当中.近年来在移动荷载领域的研究已经取得了长足的发展，Fryba［1］专著中描述了许多简单移动荷载模型，如移动常量力，移动质量以及移动弹簧质量模型.Stancioiu［2］等综合有限单元法和振型叠加法研究了若干个移动荷载通过梁桥时的跳跃现象.

移动荷载问题的解决通常基于线性振动理论，而对于结构的非线性动力学行为的研究尚不多见.随着桥梁的大跨化发展，大变形效应等因素导致结构的非线性问题越来越突出［3］.Yanmei［4］将移动荷载作用下的Euler-bernouli梁描述成一个类Duffing系统，通过多尺度法分析了参激共振.肖勇刚［5］考虑梁的几何非线性因素，建立移动荷载模型的振动方程，探讨了荷载质量、速度、桥梁阻尼和跨径等参数对车-桥耦合系统响应的影响.郭树起［6］采用改进的WKB方法求得了移动荷载作用下的梁桥跨中响应，结果表明该方法提高了传统方法精度.Tian［7］等将移动荷载模型简化为一类几何非线性弹簧振子，研究了系统长时间的混沌动力学行为.Yang［8］等建立了考虑轴向受力的移动荷载模型，利用最简规范形讨论了系统的余维2分岔.

随机Melnikov理论是将Melnikov过程和均方准则相结合的方法分析随机动力系统的混沌运动［9-12］.Lin和Yim［9］利用随机Melnikov方法研究了谐和激励和白噪声作用下的Duffing系统，发现噪声可以扩大混沌域.刘雯彦等［10-12］利用随机Melnikov方法分别研究了有界噪声和谐和激励共同作用下Duffing系统、Duffing-rayleigh系统混沌运动，通过最大Lyapunov指数，安全盆等指标说明混沌运动临界值随噪声强度的增大而增大.Yang等将随机Melnikov方法应用到车辆、船舶等工程领域的随机混沌分析中［13-14］.

目前移动荷载的相关研究一般较少考虑弹性梁表面随机因素影响.为了能够定性分析移动荷载通过弹性梁时，粗糙表面对梁跨中响应的影响.考虑了弹性梁的非线性因素以及不同等级表面平整度引起的随机冲击力，建立简支梁在随机激励和连续移动荷载作用下的非线性动力学方程.其次根据随机Melnikov方法得到混沌发生的阈值.最后应用随机Runge-Kutta法对动力学方程求解，通过最大Lyapunov指数和Poincaré截面和说明了荷载质量和不同等级表面平整度对系统的影响，得到与理论分析一致的结果.

1 模型建立

如图1：质量为M移动荷载匀速从表面不平整的简支弹性梁上通过，梁的长为L，荷载的速度为v，梁的动力学控制方程为［15］：

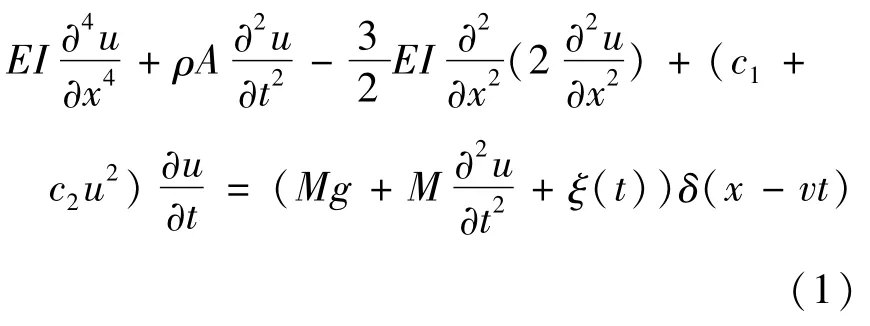
其中EI，u（x，t）分别是梁的抗弯刚度和位移函数，γ为桥梁的体密度，A为横截面积，c1，c2分别为线性、非线性阻尼系数，δ为单位脉冲函数，ξ（t）为梁表面不平整度对荷载的随机位移扰动.

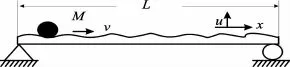
图1 移动荷载系统模型Fig.1 Schematic of moving load system

一般而言，简支梁的低阶模态对响应的贡献较大.因此为了方便研究移动荷载模型，可将振型假设成一阶模态为：

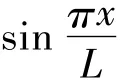
（3）式可以写成：

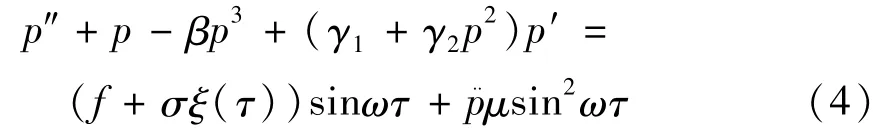
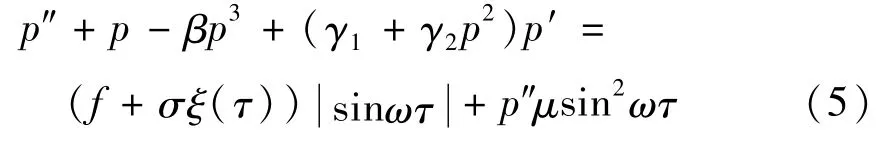
方程（5）写成状态方程：

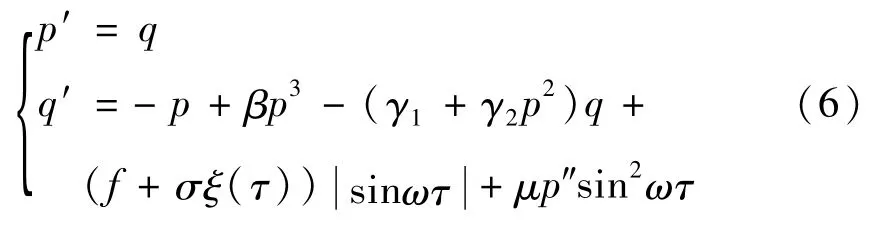
2 随机Melnikov过程

引进尺度变换γ1→εγ1，γ2→εγ2，μ→εμ，σ→εσ，f→εf，（6）式可写成具有扰动项的Hamilton系统：

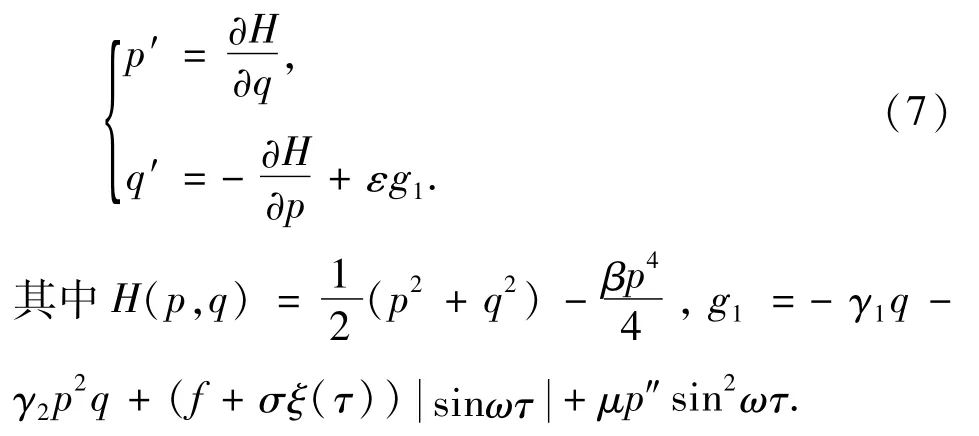
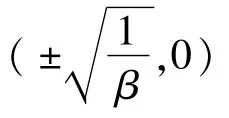
通过积分可以求得连接鞍点的异宿轨道：

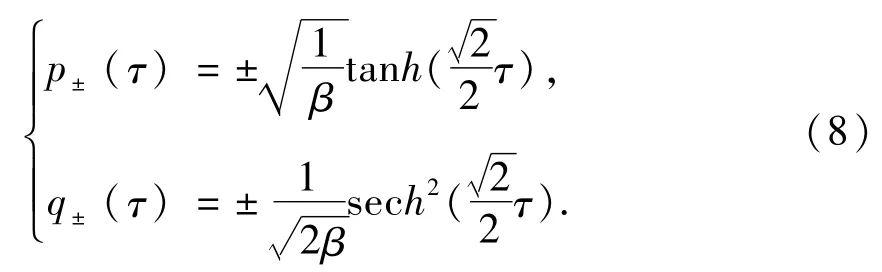
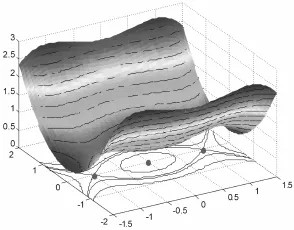
图2 b＝1时的势能函数以及异宿轨道.Fig.2 Potential energy function and heteroclinic orbit for b＝1.

判断系统出现混沌的Melnikov函数可以表示成：

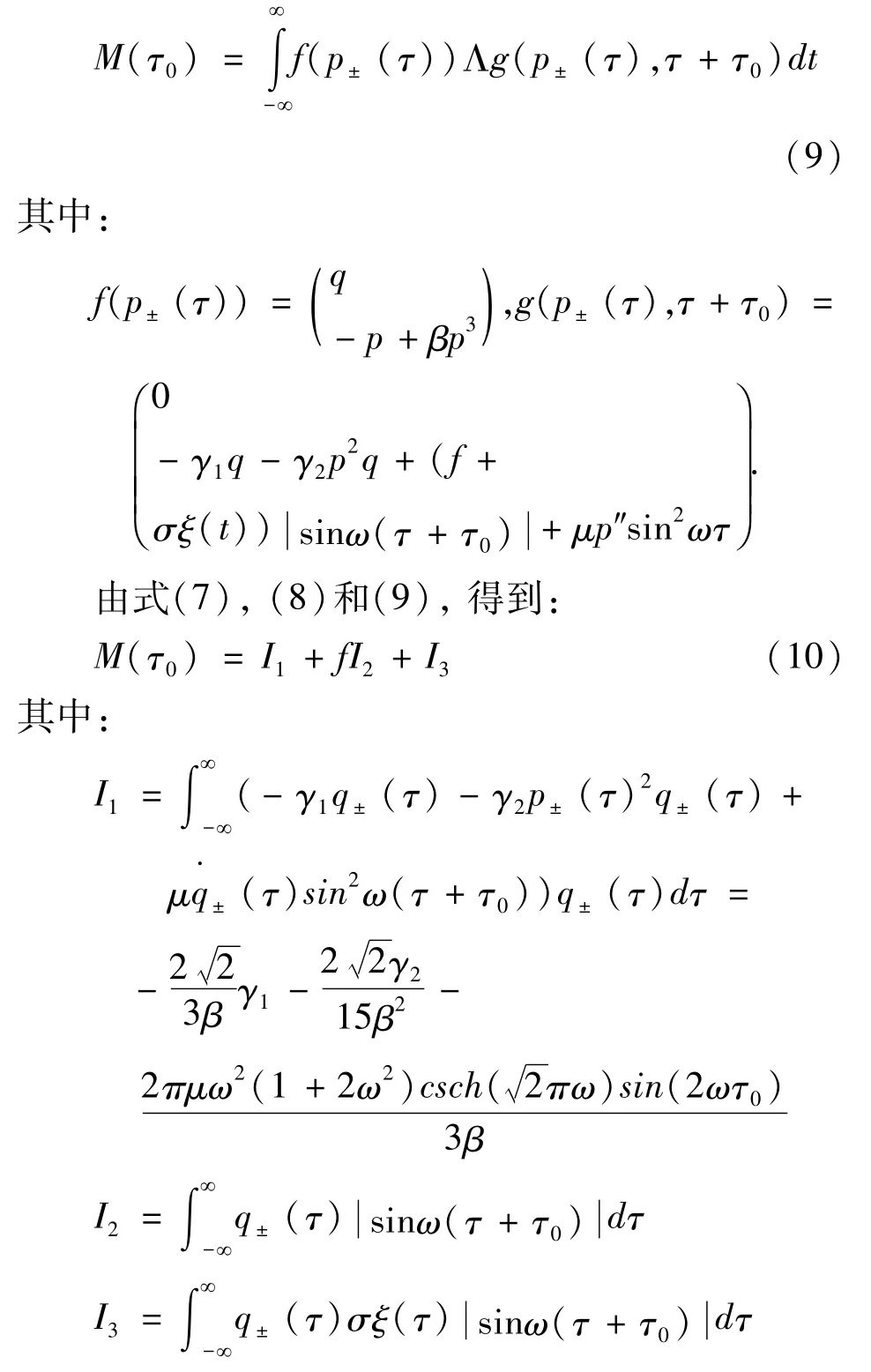
对（10）式中的｜sinω（τ+τ0）｜傅里叶展开，则有

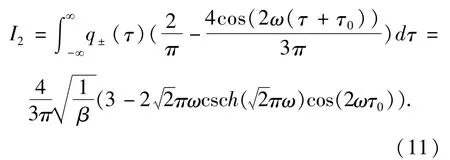
由于I3是均值为0的随机函数，因此均值意义的随机Melnikov过程等价于系统只受到确定性激励的情形.为了研究随机激励对系统的影响，需要将随机Melnikov过程和均方准则相结合［9-11］.I3的均方形式可以写成：

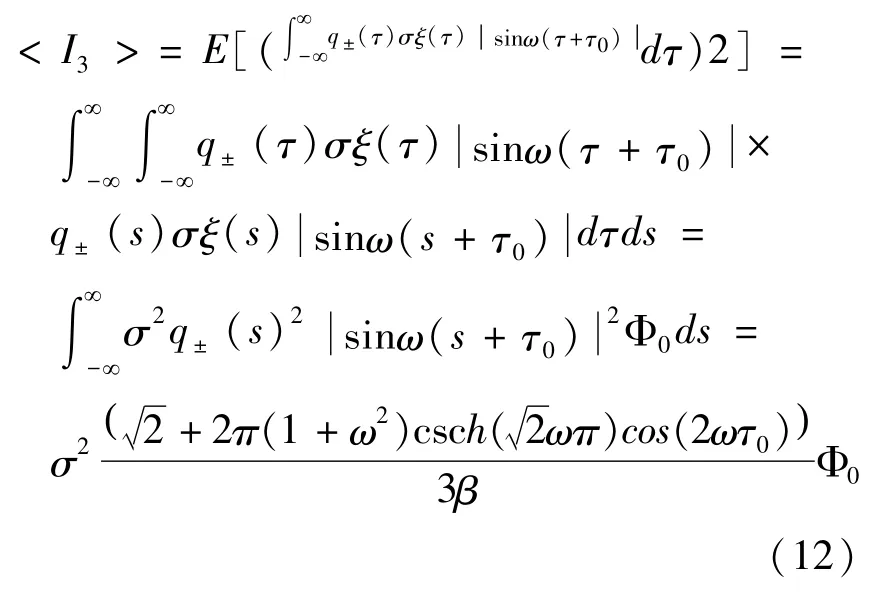
其中Φ0为不平整桥面的功率谱密度，可以看出要使Melnikov函数在均方意义下存在简单零点即〈M（τ0）〉＝0成立，当且仅当

等式（13）成立是发生随机混沌的必要条件，但并不是发生随机混沌的充分条件.下面将给出最大Lyapunov指数和Poincaré截面来判断系统是否出现混沌运动.

3 数值模拟

梁表面的不平整性引起的随机激励是一个近似各态历经的平稳随机过程，时域模型可以写成［16］

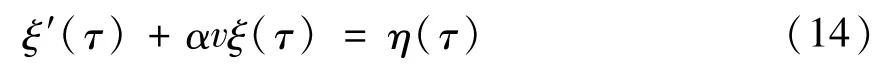
式中ξ（τ）为表面不平整输出，v为荷载的速度，η（τ）为Gauss白噪声，其协方差满足E（η（τ+ τ0）η（τ））＝2λ2αvδ（τ0）.α和λ为和表面平整度等级有关的常数（具体见表2），τ0为时移，Ω为行程圆频率.

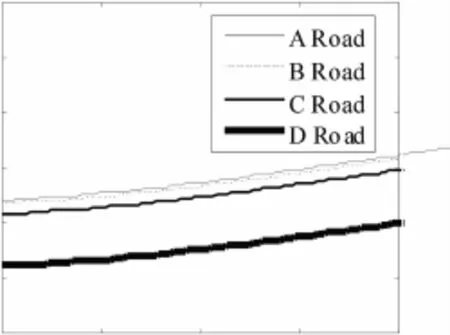
图3 混沌阈值曲线Fig.3 Chaos criteria

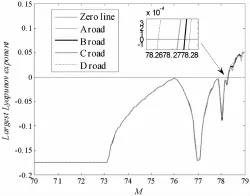
图4 不同表面平整度情形下关于荷载质量的最大Lyapunov指数图Fig.4 Argest Lyapunov exponent versus load mass

图3为公式（13）取表1、表2中的基本参数得到关于w，f的Melnikov混沌阈值曲线.当系统（6）的相关参数满足等式（13）时，随机Melnikov函数就有可能存在均方情形下的简单零点τ0，即可能产生Smale马蹄映射意义下混沌.可以看出随着弹性梁表面平整度等级的降低，关于激励幅值f产生混沌的临界值减小了.因此，在弹性梁表面平整等级较差的情形下，需要相应控制荷载的质量、速度才能有效抑制系统的混沌响应.

最大Lyapunov指数以及Poincaré截面是判断非线性动力学行为的可靠定量方法，反应了相空间的运动轨迹由于初值敏感性呈现指数收敛或发散.系统的Lyapunov指数为正，说明系统存在混沌运动，这个结论对于确定性动力系统和随机动力系统都适用.通过方程（14），以及表1、表2中的参数得到了随机激励时域形式.固定其它参数，只改变参数M，利用四阶定步长Runge-Kutta法可以得到随M变化的Lyapunov指数谱.当最大Lyapunov指数由负为正的时候，对应的M值即是发生混沌运动的门槛值.图4所示为不同平整度条件下，关于M的最大Lyapunov指数图.可以看出随着表面平整度级别降低，随机运动最终导致混沌发生的门槛值提前，混沌发生的参数区域增大.

表1 系统（3）原参数Table 1 Original parameter of system（3）

表2 梁表面平整度等级与功率谱参数α，λ值［16］Table 2 Road roughness and values of power spectral density parameter α，λ［16］

图5 M＝74kg时不同等级表面平整度的相图和庞加莱截面图.⒜A级表面；⒝B级表面；⒞C级表面；⒟D级表面.Fig.5 Phase diagrams and Poincaré sections under different roughness for M＝74kg.⒜A-roughness；⒝B-roughness；⒞C-roughness；⒟D-roughness.

图6 M＝77.5kg时不同等级表面平整度的相图和庞加莱截面图.⒜A级表面；⒝B级表面；⒞C级表面；⒟D级表面.Fig.6 Phase diagrams and Poincaré sections under different roughness for M＝77.5kg.⒜A-roughness；⒝B-roughness；⒞C-roughness；⒟D-roughness.

图7 M＝78.3kg时不同等级表面平整度的相图和庞加莱截面图.⒜A级表面；⒝B级表面；⒞C级表面；⒟D级表面.Fig.7 Phase diagrams and Poincaré sections under different roughness for M＝78.3kg.⒜A-roughness；⒝B-roughness；⒞C-roughness；⒟D-roughness.

为了进一步验证上述结论的正确性，图5-图7给出了M＝74kg、M＝77.5kg、M＝78.3kg时系统关于不同等级表面的相平面图和Poincaré截面图.在图5（a）-图5（d）中可以看出Poincaré截面为随机的一团点，此时可以判定系统在不同等级表面的激励下保持随机周期-1运动状态.

从图6（a）-图6（b）看出Poincaré截面为随机的两团点，此时系统运动可以判定为随机周期-2运动，而图6（c）-图6（d）中的周期运动呈现出模糊的发散状态，表明表面平整度等级的降低增加了外在随机激励强度，非线性系统的内在的随机响应被激发出来.

在图7中，由于荷载质量M已经达到发生混沌运动的临界值，Poincaré截面充满相空间的某一部分，并且呈现出自相似结构，可以判定此时系统发生混沌运动.

4 结论

分析了随机激励下移动荷载模型，通过随机Melnikov理论得到了随机混沌产生的参数范围，基于不同表面平整度得到了不同等级的随机激励并且数值计算简支梁跨中非线性随机响应。得到以下结论：

（1）随机Melnikov方法得到的关系式表明，随着表面平整度等级的降低，产生混沌的临界激励幅值减小，导致混沌域的参数空间增大.

（2）数值模拟发现系统发生混沌运动的门槛值随着表面平整度的降低而减小，表明表面不平整的弹性梁增加了混沌运动的可能性.这与（1）所得到的理论解释相一致.

（3）在给定的参数下，系统存在混沌发生的可能性.在相同平整度等级的条件下，荷载的质量小于临界值时系统呈现随机运动，当质量超过临界值时出现混沌运动.

1 Fryba L.Vibration of solids and structures under moving loads.London：Telford，1999：87

2 Stancioiu D，Ouyang H，Mottershead J E.Vibration of a beam excited by a moving oscillator considering separation and reattachment.Journal of Sound and Vibration，2008，310（4）：1128～1140

3 Nayfeh A H，Mook D T.Nonlinear oscillations.New York：John Wiley＆Sons，1979

4 Yanmeni W A N，Tchoukuegno R，Woafo P.Nonlinear dynamics of an elastic beam under moving loads.Journal of Sound and Vibration，2004，273（4）：1101～1108

5 肖勇刚，朱素红.车桥耦合系统的非线性动力分析.振动与冲击，2007，26（8）：104～108（Xiao Y G，Zhu S H.Nonlinear dynamic analysis of vehicle-bridge coupled interaction system.Journal of Vibration and Shock，2007，26（8）：104～108（in Chinese））

6 郭树起，孔艳平，杨绍普.简支梁移动质量响应分析.动力学与控制学报，2014，12（1）：56～61（Guo S Q，Kong Y P，Yang S P.Analysis of the dynamic response of a simple supported beam under moving mass.Journal of Dynamics and Control，2014，12（1）：56～61（in Chinese））

7 Tian R L，Yang X W，Cao Q J.The study on the mid-span deflection of a beam bridge under moving loads based on SD oscillator.International Journal of Bifurcation and Chaos，2012，22（5）：1250108

8 Yang X W，Tian R L，Li H T.Codimension-two bifurcation of axial loaded beam bridge subjected to an infinite series of moving loads.Chinese Physic B，2013，22（12）：120502

9 Lin H，Yim S C S.Analysis of a nonlinear system exhibiting chaotic，noisy chaotic，and random behavior.ASME Journal of Applied Mechanics，1996，63（2）：509～516

10 刘雯彦，朱位秋，黄志龙.有界噪声参激下Duffing振子的混沌运动.工程力学，1999，16（6）：133～136（Liu W Y，Zhu W Q，Huang Z L.Chaotic motion of Duffing oscillator under parametric excitation of bounded noise.Engineering Mechanics，1999，16（6）：133～136（in Chinese））

11 冯俊，徐伟，顾仁财.有界噪声与谐和激励联合作用下Duffing-rayleigh振子Melnikov混沌.物理学报，2011，60（9），090507（Feng J，Xu W，Gu R C.Melnikov chaos in Duffing-rayleigh oscillator subjected to combined bounded noise and harmonic excitations.Acta Physica Sinica，2011，60（9）：090507（in Chinese））

12 葛根，竺致文，许佳.形状记忆合金梁在简谐和白噪声联合激励下的混沌及安全盆侵蚀现象.振动与冲击，2012，31（23）：1～4（Ge G，Zhu Z W，Xu J.Chaos and fractal boundary of safe basin of shape memory alloy beam subjected to simple harmonic and white noise.Journal ofVibration and Shock，2012，31（23）：1～4（in Chinese））

13 Yang S P，Chen L Q，Li S H.Dynamics of vehicle-road coupled system.New York：Springer-Verlag，2014

14 刘利琴，唐友刚.基于随机Melnikov方法的甲板上浪船舶混沌运动研究.船舶力学，2011，15（10）：1075～1081（Liu L Q，Tang Y G.Study on chaotic motion of ship with water on deck using random Melnikov method.Journal of Ship Mechanics，2011，15（10）：1075～1081（in Chinese））

15 Kovacic I，Brennan M J.The Duffing equation：nonlinear oscillators and their behaviour.New York：John Wiley＆Sons，2011

16 吴志成，陈思忠，杨林等.基于有理函数的路面不平度时域模型研究.北京理工大学学报，2009，29（9）：795～798（Wu Z C，Chen S Z，Yang L，et al.Model of road roughness in time domain based on rational function.Transactions of Beijing Institute of Technology，2009，29（9）：795～798（in Chinese））

Recived 22 November 2014，revised 9 December 2014.

*The project supported by the National Natural Science Foundation of China（11272257，11172234）

†Corresponding author E-mail：qinweiyang@aliyun.com

BIFURCATION ANDCHAOS OF BEAM SUBJECTED TO MOVING LOADS AND RANDOM EXCITATIONS*

Li Haitao1Qin Weiyang1†Tian Ruilan2
（1.Department of Engineering Mechanics，Northwestern Polytechnical University，Xi’an 710072，China）（2.Department of Mathematics and Physics，Shijiazhuang Tiedao University，Shijiazhuang 050043，China）

moving loads pass through the rough surface of beam.Considering the characteristics of random excitation，present nonlinear model of moving loads different beam roughness.The critical condition in of mean square is obtained by random Melnikov process.The response of structure under the combin of random and periodic excitation is simulated，and used to the variation of dynamic behaviors.It is concluded that speed，nonlinear dynamic behaviors mid-span of beam are severely influenced by the random excitation.Therefore poor flatness of surface would increase the probability of occurrence of chaos.

road roughness，random Melnikov process，moving loads，chaos

10.6052/1672-6553-2015-010

2014-11-22收到第1稿，2014-12-09收到修改稿.

*国家自然科学基金资助项目（11272257，11172234）

†通讯作者E-mail：qinweiyang@aliyun.com