空间太阳能电站太阳能接收器二维展开过程的保结构分析*

王新栋胡伟鹏邓子辰，2†

（1.西北工业大学力学与土木建筑学院，西安 710072）（2.大连理工大学工业装备结构分析国家重点实验室，大连 116023）

空间太阳能电站太阳能接收器二维展开过程的保结构分析*

王新栋1胡伟鹏1邓子辰1，2†

（1.西北工业大学力学与土木建筑学院，西安 710072）（2.大连理工大学工业装备结构分析国家重点实验室，大连 116023）

针对传统数值方法求解微分-代数方程过程中经常遇到的违约问题，本文以空间太阳能电站太阳能接收器的简化二维模型为例，采用辛算法模拟了简化模型的展开过程，研究了辛算法在求解过程中约束违约问题.首先，基于Hamilton变分原理，将描述简化二维模型展开过程的Euler-Lagrange方程导入Hamilton体系，建立其Hamilton正则方程；随后，采用s级PRK离散方法离散正则方程，得到其辛格式；最后，采用辛PRK格式模拟太阳能接收器的二维展开过程.模拟结果显示：本文构造的辛PRK格式能够很好地满足系统的位移约束.

辛PRK格式，保结构，空间太阳能电站

引言

太阳是一个通过电磁辐射向外不断发送能量的光源.设想在地球同步轨道上有1km宽、围绕地球一周的太阳电池条带，条带面积为266407.7km2，太阳照射在条带上的能量约为212TW/年，相当于地球目前剩余的石油所提供的能源数量（249.4TW/年）.可见，太阳能具有广阔的利用前景，而在地面利用太能能收到各种条件的限制，太阳能的利用率非常有限.于是，学术界自上世纪70年代开始，构想建立空间太阳能电站，完成太阳能的收集、太阳能向电能的转换和无线传输，从而解决人类面临的能源匮乏问题.

现代空间太阳能电站的构想最早于1968年由美国的Peter E.Glaser提出，即所谓的太阳能发电卫星SPS（Solar Power Satellite）.此后的三十年间，美国航空航天局（NASA）和能源部耗巨资对天基太阳能发电概念进行过大量的研究工作，并且提出5GW的“1979 SPS基准系统”方案；日本从20世纪80年代就开始进行SPS概念和关键技术研究，并陆续推出了SPS2000、SPS2001、SPS2002、SPS2003、分布式绳系SPS系统等设计概念；欧洲在1998年开展了“空间及探索利用的系统概念、结构和技术研究”计划，提出了名为“太阳帆塔”的概念设计［1］.为了提高空间太阳能电站的效率，NASA于2012年提出了新的空间太阳能电站构想——The SPS-ALPHA Concept（如图1）.在这种空间太阳能电站概念中，太阳能接收器的展开动力学是整个系统展开的关键步骤.

图1 NASA 2012年提出的空间太阳能电站Fig.1 Solar power satellite by NASA，2012

从图1可以看出，整个太阳能接收装置是一个回转对称周期性结构，这种结构的动力学控制方程与辛几何有着天然的联系.在接收装置展开过程中，其空间构型需要始终保持回转对称形式，这就是保结构分析中需要保持的“结构”.

保结构算法始于计算数学专家冯康1984年在双微（微分方程和微分流形）国际会议上的报告—On difference schemes and symplectic geometry［2］，其初衷是“使得问题原型的基本特征在离散后尽可能地得到保持，即离散化应该尽可能在问题原型的同一形式框架中进行”［2］；此后在计算力学领域，钟万勰对辛几何进行了通俗的表述，并将其应用于应用力学领域的数值研究［3］；Thomas J.Bridges等人建立的多辛算法能够精确保持无穷维Hamilton系统的多辛结构及其局部能量守恒律和局部动量守恒律［4-5］，将保结构思想拓宽至无穷维系统；最近，邓子辰、胡伟鹏等人针对实际力学系统中存在耗散效应这一特点，提出了广义多辛算法理论［6］，完善了保结构算法理论体系.

本文将针对图1所示的空间太阳能电站太阳能接收器的二维结构，建立其第一类Lagrange方程，并利用保结构算法思想模拟该二维结构的展开过程，为空间太阳能电站的进一步设计优化提供参考.

1 太阳能接收器的简化二维结构

与太阳帆的展开过程［7］类似，空间太阳能电站太阳能接收器也是旋转展开的.不同的是，单纯的太阳帆是平面结构，而图1所示的空间太阳能电站构想是空间结构.考虑到结构的回转对称性，我们在本文中仅考虑任一垂直于回转轴的截面的展开过程，忽略截面间的约束问题，为了问题分析的方便，本文考虑如图2所示的二维结构.

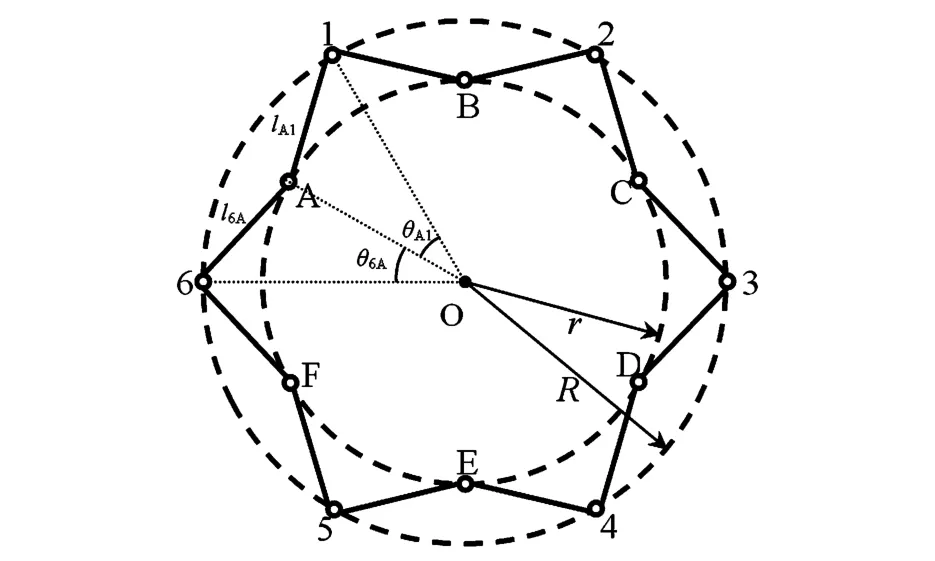
图2 空间太阳能电站太阳能接收器的简化二维结构Fig.2 Simplified 2D model of solar power receiver of solar power satellite

该简化模型中，外圈上的质点1、2、3、4、5、6质量均为M，均匀分布在半径为R的圆周上；内圈的质点A、B、C、D、E、F质量均为m，均匀分布在半径为r的圆周上；外圆和内圆同心；如图所示，外圆和内圆上的相邻质点之间的距离表示为lA1，l1B，…，l6A，由结构周期对称性，则lA1＝l1B＝…＝l6A＝l，以角度表示这种关系，则为：

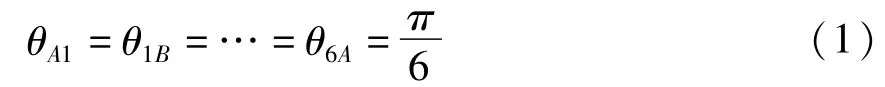
结构旋转展开过程中，由于结构的对称性和周期性，在展开过程中的任意时刻，式（1）是始终应该得到满足的.假定连接外圆和内圆上的相邻质点的杆件是质量不计的刚杆，则各杆长在展开过程中是不变的.以上这些构成了系统的完整约束.

2 简化二维结构展开的Hamilton正则方程

当二维结构以恒定的角速度ω绕O点转动时，取广义坐标（R，r），满足如下约束关系：

使用动静法，建立随展开机构平面一同转动的极坐标系，在该参考系下，系统的动能为：

忽略柯氏力的影响，则作用在系统上的广义力为：

系统修正的Lagrange函数为：

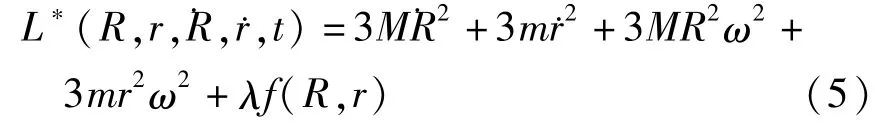
由存在m个双面约束系统的第一类Lagrange方程：

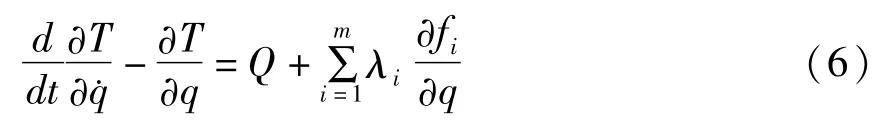
可以推导得到系统的运动方程：

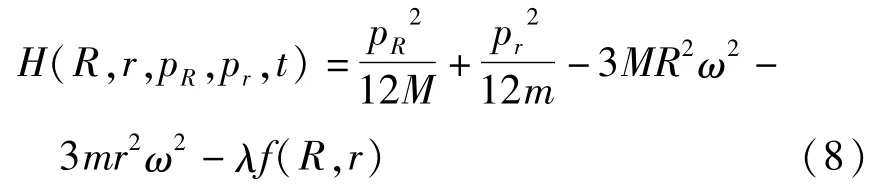
其中λ为Lagrange乘子.由Hamilton变分原理，得到Hamilton体系下的对偶正则方程组：

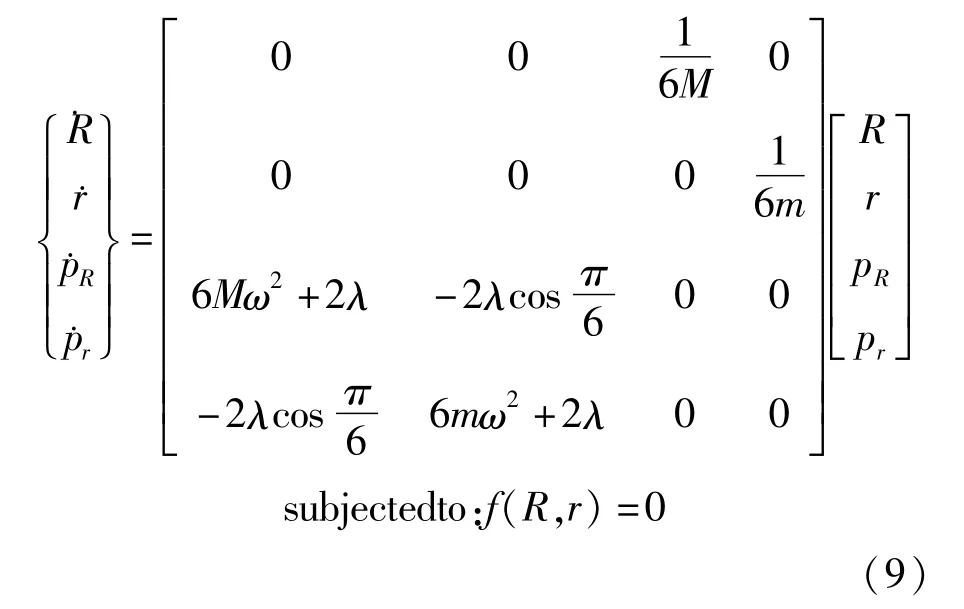
为方便后续算法构造过程叙述，将以上对偶正则方程组写成标准形式：

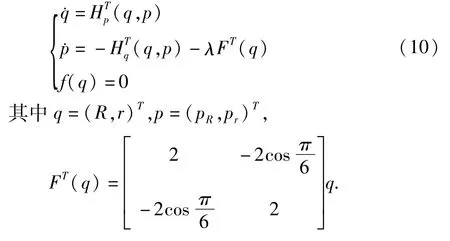
3 基于辛算法的简化二维结构展开

已有研究［8-9］表明，Hamilton体系下的对偶正则方程组（9）直接可以采用流形上的辛算法进行数值求解，在此，我们采用常见的辛PRK离散方法离散正则形式（10）.

将s级PRK方法应用于方程组（10），得：

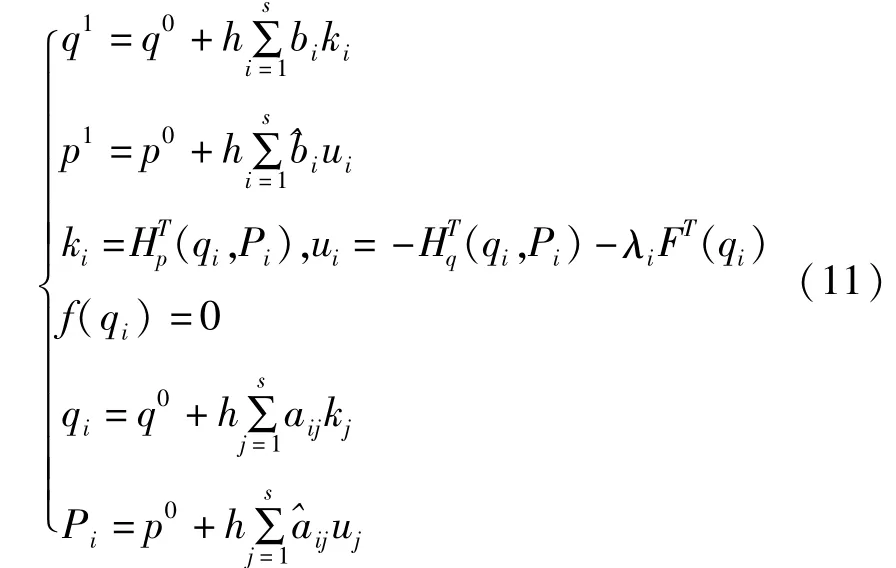
格式（11）是辛的，当且仅当其中的系数满足［9］：

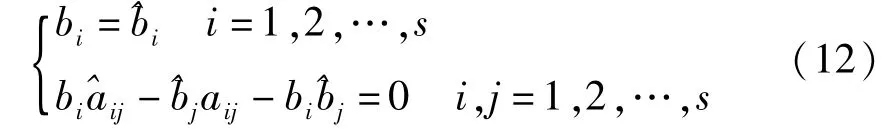
下面就采用2级PRK格式（s＝2）模拟空间太阳能电站太阳能接收器简化二维结构的展开过程，结构几何参数设为无量纲量：R＝1，r＝0.8，则l≈0.504；质点质量也设为无量纲量：m＝1，M＝0.8；结构旋转角速度设为无量纲量：ω＝1.采用2级辛PRK格式模拟结构展开过程，步长取为h＝0.5，可得各质点不同时刻位置如图3所示.

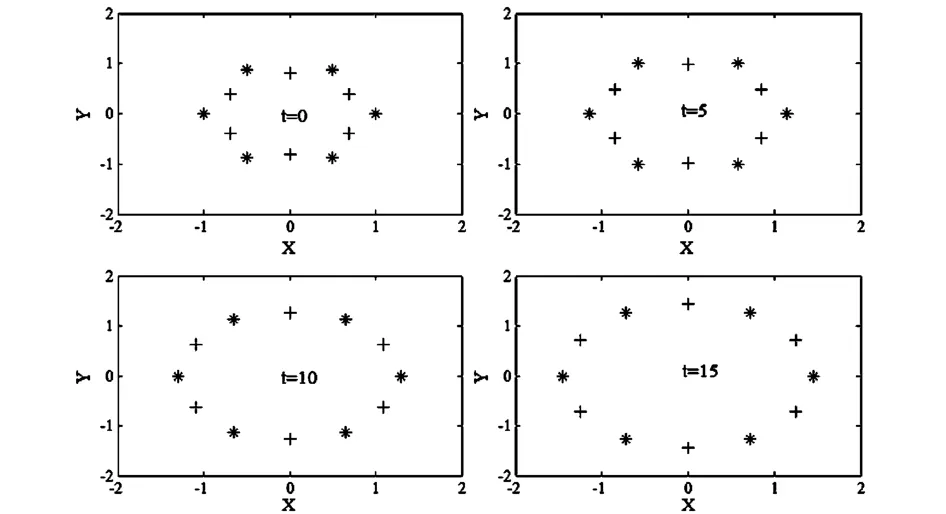
图3 不同时刻内外层质点位置（“*”标记为外层质点，“+”标记为内层质点）Fig.3 Positions of inner points（*）and outer points（+）at different time

同时得到不同时刻的位移违约情况如图4所示（图中fi为第i步f（R，r）的数值结果fi＝f（Ri，ri））.由图4可看出，在t∈［0，50］内，位移约束误差在［-2×10-9，2×10-9］范围内，这说明了辛算法具有极好的保结构性能和良好的长时间数值稳定性.

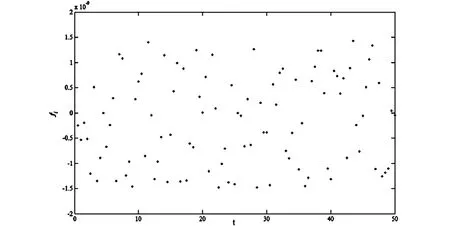
图4 位移约束违约情况Fig.4 Violations of displacement constraint

以上模拟结果表明：采用辛算法模拟空间太阳能电站太阳能接收器简化二维模型的展开过程中，针对每一时间节点，二维模型外层质点能保持在一个圆上，内层质点也能保持在另一个圆上，内层质点所在的圆比外层质点所在的圆扩张速度快.针对求解第一类Lagrange方程（DAEs）时传统算法出现严重违约的困难，本文的结果显示辛算法能够很好地克服约束违约的情况.

4 结论

微分-代数方程数值求解过程中的约束违约问题是多体动力学问题数值分析的难以解决的问题.本文针对空间太阳能电站太阳能接收器简化的二维模型为研究对象，建立了其Euler-Lagrange方程，并基于Hamilton变分原理将其导入了Hamilton体系下，得到正则方程形式；利用辛PRK离散方法建立了正则方程的s级辛PRK格式，并用于模拟二维简化模型的展开过程.模拟结果显示，在长时间数值模拟过程中，构造的辛PRK格式能够在每一个时间节点上保持太阳能接收器在展开过程的几何特性，并满足相应的位移约束条件.本文的研究虽然是以二维简化模型为例进行的展开过程模拟，如果考虑面外的约束，容易将本文的方法推广至三维模型情况.本文的研究结果将为空间太阳能电站太阳能接收器的结构设计和展开方案设计提供参考.

1 张钧屏.空间太阳能电站构想及其相关技术的发展.航天返回与遥感，2011，32（5）：10～18（Zhang J P.The concept of solar power satellite（SPS）and its key technologies.Spacecraft Recovery＆Remote Sensing，2011，32（5）：10～18（in Chinese））

2 Feng K.On difference schemes and symplectic geometry.Proceeding of the 1984 Beijing Symposium on D.D.，Beijing：Science Press，1984：42～58

3 钟万勰.应用力学的辛数学方法.北京：高等教育出版社，2006（Zhong W X.Symplectic solution methodology in applied mechanics.Beijing：Higher Education Press，2006（in Chinese））

4 Bridges T J.Multi-symplectic structures and wave propagation.Mathematical Proceedings of the Cambridge Philosophical Society，1997，121（1）：147～190

5 Bridges T J，Reich S.Multi-symplectic integrators：numerical schemes for hamiltonian PDEs that conserve symplecticity.Physics Letters A，2001，284（4-5）：184～193

6 Hu W P，Deng Z C，Han S M，Zhang W R.Generalized multi-symplectic integrators for a class of hamiltonian nonlinear wave PDEs.Journal of Computational Physics，2013，235：394～406

7 胡海岩，田强，张伟，金栋平，胡更开，宋燕平.大型网架式可展开空间结构的非线性动力学与控制.力学进展，2013，43（4）：390～414（Hu H Y，Tian Q，Zhang W，Jin D P，Hu G K，Song Y P.Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes.Advances in Mechanics，2013，43（4）：390～414（in Chinese））

8 黄永安，尹周平，邓子辰，熊有伦.多体动力学的几何积分方法研究进展.力学进展，2009（1）：44～57（Huang Y A，Yin Z P，Deng Z C，Xiong Y L.Progress in geometric integration method for multibody dynamics.Advances in Mechanics，2009（1）：44～57（in Chinese））

9 吴永，胡继云，殷学纲.多体系统动力学方程在流形上的辛算法.力学进展，2002，32（2）：189～195（Wu Y，Hu J Y，Yin X G.Symplectic integrators of the equations of multibody system dynamics on manifolds.Advances in Mechanics，2002，32（2）：189～195（in Chinese））

Received 14 September 2013，revised 11 October 2013.

*The project supported by Key Program of National Natural Science Foundation of China（11432010）and the Doctoral Program Foundation of Education Ministry of China（20126102110023）

†Corresponding author E-mail：dweifan@nwpu.edu.cn

STRUCTURE-PRESERVING ANALYSIS OF 2D DEPLOYING PROCESS FOR SOLAR POWER RECEIVER OF SOLAR POWER SATELLITE*

Wang Xindong1†Hu Weipeng1Deng Zichen1，2
（1.Department of Engineering Mechanics，Northwestern Polytechnical University，Xi′an 710072，China）（2.State Key Laboratory of Structural Analysis of Industrial Equipment，Dalian University of Technology，Dalian 116023，China）

The constraints default phenomenon is a serious problem in solving the I-type Lagrange equation with traditional numerical method.For the simplified 2D model of the solar power receiver of Solar Power Satellite（SPS），the symplectic method is used to analyze the deploying process of the solar power receiver and the constraints default is discussed in this paper.Firstly，based on the Hamilton variational principle，the canonical equation is derived from the Euler-Lagrange equation that describe the deploying process of the solar power receiver.And then，the symplectic PRK scheme for the canonical equation is constructed.Finally，the deploying process of the solar power receiver is simulated by the symplectic PRK scheme.From the simulation results，it can be concluded that the symplectic PRK scheme constructed in this paper can satisfy the displacement constraint of the 2D system well for a long time.

symplectic PRK scheme，structure-preserving，Solar Power Satellite（SPS）

10.6052/1672-6553-2014-032

2013-09-14收到第1稿，2013-10-11收到修改稿.

*国家自然科学基金重点资助项目（11432010）和高校博士点基金资助项目（20126102110023）

†通讯作者E-mail：dweifan@nwpu.edu.cn