二重动力吸振器在汽车振动控制中的应用
李筱筱,陈艺梦
(长安大学汽车学院,陕西 西安 710064)
前言
随着社会的发展,汽车已经成为主要的交通工具,人们对汽车乘坐舒适性的要求越来越高。汽车行驶过程中,因发动机或路面激励造成的零部件共振是影响乘坐舒适性的主要原因。因此,对汽车振动的控制一直是各个企业以及国内外学者研究的重点。
传统动力吸振器因简单的结构、良好的减振性能在汽车振动领域得到广泛应用。刘杰为降低某汽车发动机制动踏板抖动严重的问题,基于吸振器最有阻尼比关系设计了不同质量比的动力吸振器[1]。姜骏等人针对汽车方向盘抖动异常抖动的问题,设计了不同固有频率的吸振器,并通过实验分析吸振器的减振性能[2]。何山设计了一款结构简单的动力吸振器,并将其应用于车辆副车架上,解决因副车架纵梁共振造成的车内后排噪声过大的问题[3]。刘国政利用动力吸振器抑制某车辆驱动桥的振动,降低了车内噪声[4]。赵健兵在汽车后背门上安装吸振器,使因后背门共振造成的车内噪声明显降低[5]。
传统动力吸振器虽然可以在其工作点有效抑制汽车零部件的振动,但是传统动力吸振器减振频带窄,而且汽车激振频率多变,可能使被控对象对于新的共振状态,减振效果恶化。此时,若能降低被控对象频率响应的共振峰,将有利于提升动力吸振器的工作性能。本文提出了二重动力吸振器,并分析了其减振性能。
1 传统动力吸振器
汽车振动控制中通常在被控对象上安装动力吸振器以降低被控对象的振动幅度。传统动力吸振器相当于一个“质量-弹簧-阻尼”系统,安装在单自由度主系统(即被控对象)的吸振器模型如图1所示。

图1 传统动力吸振器模型
图中,mz、kz、cz、m1、k1、c1分别表示主系统与吸振器的质量、刚度与阻尼系数;xz、x1分别表示主系统与吸振器的位移;Fzsinωt表示作用于主系统上的激振力,ω为外界激振频率。对图1中的模型进行分析,可得系统的动力学方程为:

引入吸振器与主系统质量比μ=m1⁄mz,吸振器与主系统固有频率比γ=ω1⁄ωz,外界激振频率与主系统固有频率比λ=ω⁄ωz。其中主系统与吸振器固有频率ωz与ω1分别为定义主系统阻尼比ξz与吸振器阻尼比ξ1分别为:ξz=cz⁄ (2mzωz),ξ1=c1⁄(2m1ω1)。将上述符号代入式(1)可得主系统频率响应函数表达式为:

根据式(3)可做吸振器不同阻尼比时主系统频率响应曲线,如图2所示。
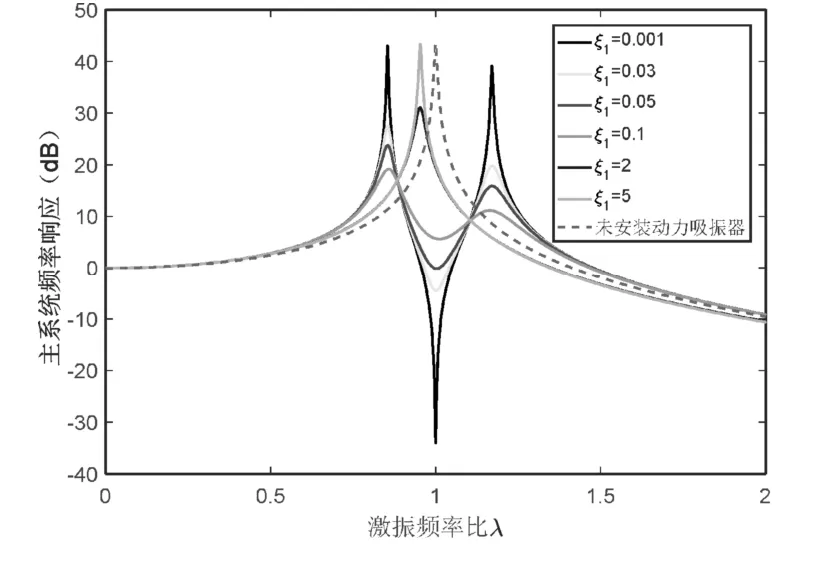
图2 吸振器不同阻尼比时主系统频率响应曲线
从图2可以看出,当动力吸振器阻尼比ξ1很小(例如ξ1=0.001)时,吸振器减振效果好,但主系统频率响应共振峰高。一旦激振频率发生变化,主系统有可能发生共振。随着吸振器阻尼比的增加,吸振器减振效果变差,同时主系统共振峰有所降低。当吸振器阻尼比很大时,吸振器相当于固定在主系统上,主系统频率响应与不安装动力吸振器时类似只有一个共振峰。在设计动力吸振器时通常要保证吸振器的减振效果的同时主系统共振峰又不能太高,吸振器的阻尼不宜过小。若能降低小阻尼吸振器的共振峰,则有利于提升吸振器的减振性能。为此本文提出了二重动力吸振器。
2 二重动力吸振器
2.1 二重动力吸振器建模
二重动力吸振器将两个传统动力吸振器组合使用,其中一个作为主吸振器减低主系统的振动,另一个则用来降低安装动力吸振器后主系统共振峰,防止激振频率偏移时,主系统出现过大振动。二重动力吸振器模型如图2所示。将两个动力吸振器分别记为吸振器1与吸振器2。
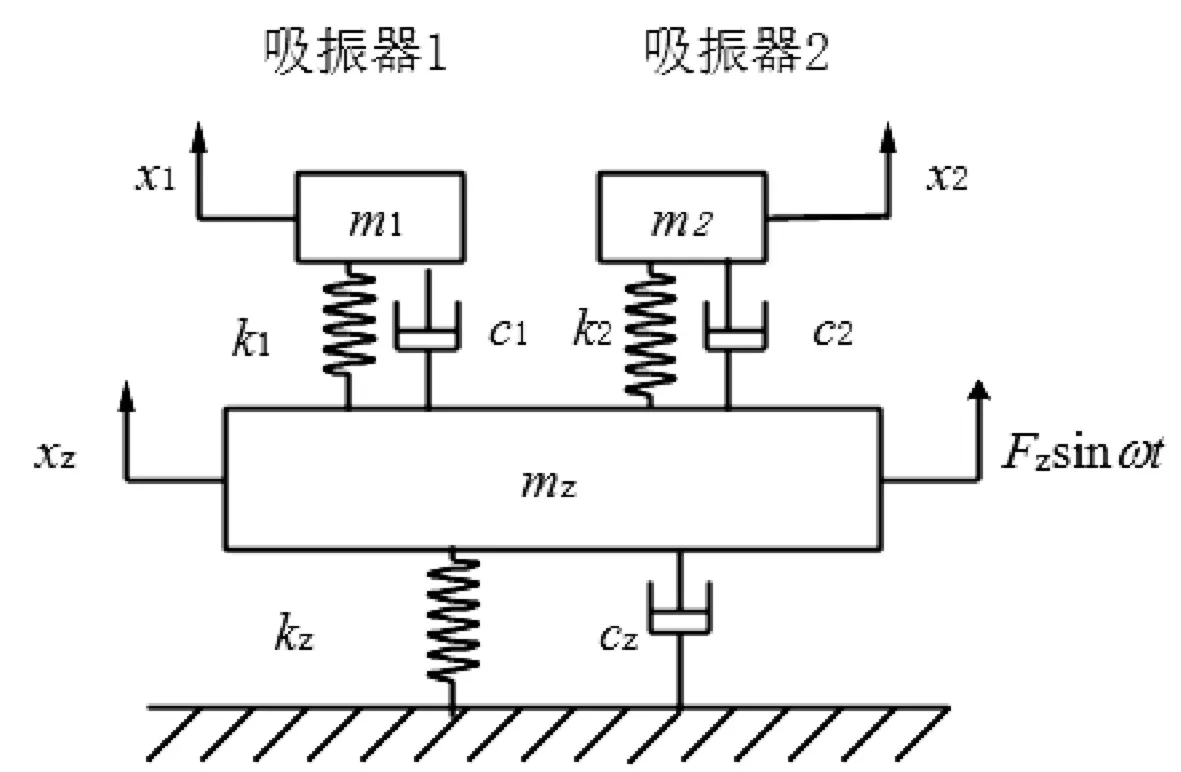
图3 二重动力吸振器模型
图中mz、m1、m2分别表示主系统与吸振器的质量;kz、k1、k2分别表示主系统与吸振器的刚度;cz、c1、c2分别表示主系统与吸振器的阻尼系数;Fzsinωt表示作用于主系统上的激振力,ω为外界激振频率。根据牛顿定理可得二重吸振器模型的动力学方程为:
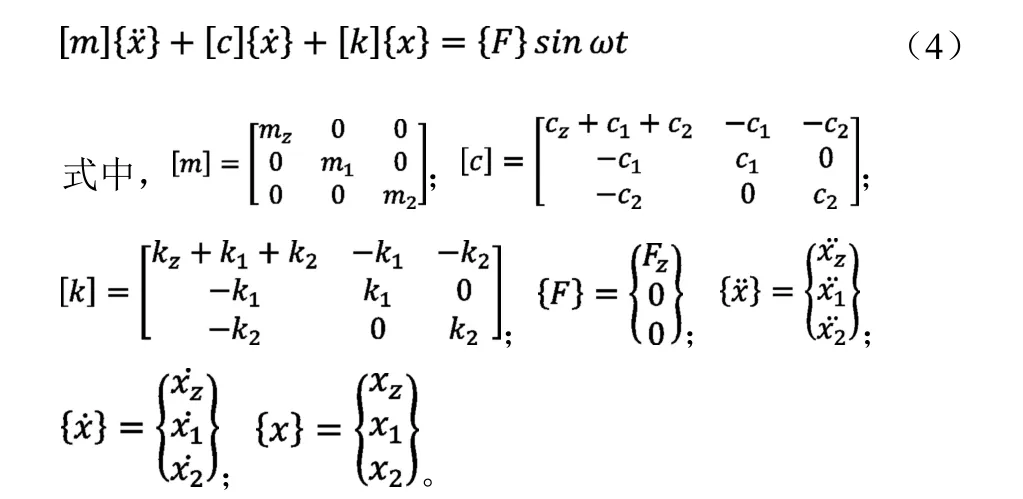
求解式(4)可得安装二重动力吸振器的主系统频率响应函数为:

2.2 二重动力吸振器减振性能
传动动力吸振器的减振效果受吸振器阻尼的影响。在此假设吸振器1固有频率小于吸振器2固有频率,根据式(5)分析吸振器不同阻尼比ξ1与ξ2对主系统频率响应的影响,如图4与图5所示。其中ξ1=c1⁄(2m1ω1);ξ2=c2⁄(2m2ω2)。
从图4可以看出,随着吸振器1阻尼比ξ1增加,其固有频率处减振效果变差,但是主系统频率响应的共振峰均有所下降。从图5可以看出,随着吸振器2阻尼比ξ2的增加,其固有频率处减振效果变差,主系统第二与第三个共振峰降低,但是吸振器2阻尼比的变化对主系统第一个共振峰影响不大。二重吸振器中一个吸振器阻尼比的变化,不会影响另一个吸振器固有频率处的减振效果。当吸振器1有较大阻尼比时(例如ξ1=0.1)主系统共振峰峰值较低。
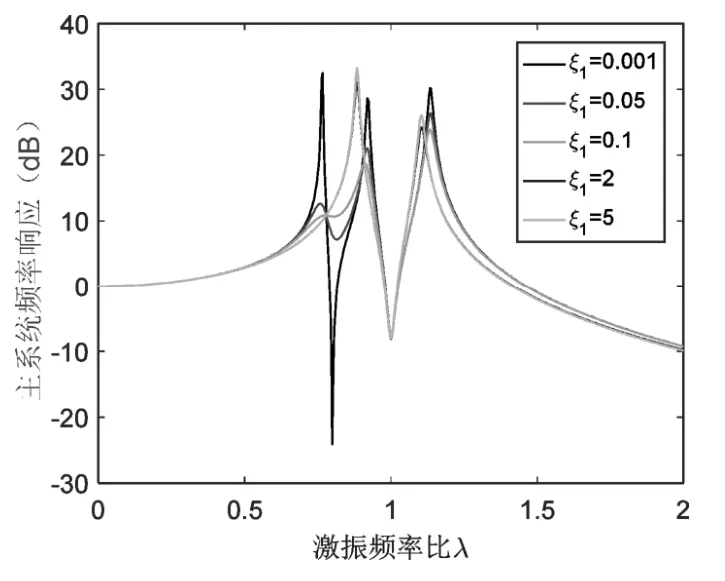
图4 吸振器1阻尼对主系频率响应的影响

图5 吸振器2阻尼对主系频率响应的影响
二重动力吸振器中,若以固有频率大的吸振器作为主吸振器,使其具有小阻尼以获得良好的减振效果;另一个吸振器具有较大的阻尼系数以降低主系统共振峰。那么二重吸振器具有良好减振效果同时主系统共振峰有较低。为对比二重动力吸振器与传统动力吸振器的减振效果,假设吸振器2结构参数与传统动力吸振器相同,作安装二重动力吸振器与仅安装传统吸振器时主系统的频率响应,如图6所示。图中,红色对应传统动力吸振器,黑色对应二重动力吸振器。

图6 二重动力吸振器与传统动力吸振器对比
从图6可以看出,二重动力吸振器与传统动力吸振器减振效果相同,但是二重动力吸振器对应的主系统共振峰更低。这就意味着,即使汽车行驶过程中,因发动机或者路面所造成的激振频率发生变化,安装二重动力吸振器的零部件处于共振时的振动幅度较安装传统动力吸振器的零部件振动幅度低,不会引起新的共振问题。
3 仿真与分析
根据前文分析,在二重动力吸振器中令固有频率较小的吸振器(吸振器1)具有较大的阻尼比(阻尼比为0.1),同时固有频率较大的吸振器(吸振器2)具有较小的阻尼系数;吸振器1固有频率为0.8ωz,其中为ωz主系统固有频率;吸振器2固有频率与ωz相等。主系统与吸振器结构参数如表1所示。验证二重动力吸振器的减振效果,在MATLAB/Simu- link软件中搭建二重动力吸振器模型与传统动力吸振器模型。其中传统动力吸振器与二重吸振器中吸振器2参数相同。
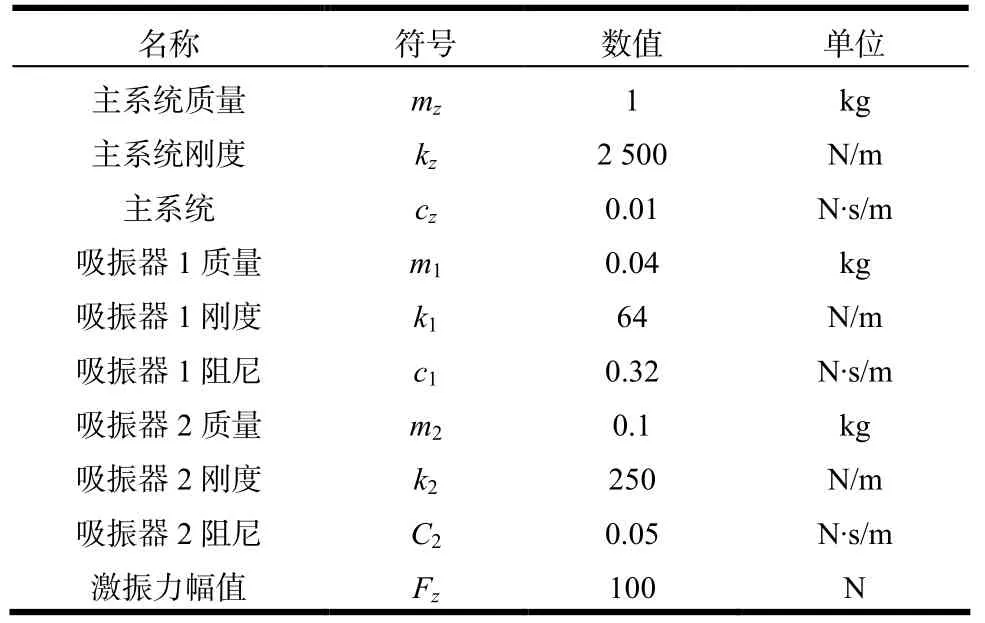
表1 主系统与吸振器参数
从表1可知主系统的固有频率为50 rad/s。令激振频率ω在0~10 s内从0 rad/s逐渐增加到50 rad/s。利用搭建好的模型仿真安装二重动力吸振器与仅安装传统动力吸振器的主系统位移变化,如图7与图8所示。

图7 安装传统动力吸振器对应的主系统位移

图8 安装二重动力吸振器对应的主系统位移
从图7可以看出,0~10 s时,激振频率ω从0 rad/s逐渐增加至50 rad/s,仅安装传统动力吸振器的主系统振动幅度逐渐增大至0.058 m。10 s~50 s激振频率ω=50 rad/s,此时激振频率与吸振器固有频率相同,主系统振动幅度逐渐降低。大约30 s时,主系统处于稳态振动。从图8可以看出,0~10 s时,随着激振频率ω从0 rad/s增大到50 rad/s,仅安装二重动力吸振的主系统振动逐渐增大,最大振动幅度为0.0258 m。10 s~50 s激振频率ω=50 rad/s,此时ω与二重动力吸振器中吸振器2固有频率相同,主系统振动迅速衰减。大约15 s系统达到稳定状态,且稳态振幅与安装传统动力吸振器的主系统稳态振幅相同。
对比图7与图8可以发现,当激振频率逐渐增大至主系统固有频率的变化过程中,安装二重动力吸振器的主系统振动幅度较仅安装传统动力吸振器的主系统振动幅度明显更低。因为二重动力吸振器中阻尼较大,主系统可以更快的达到稳态振动。所以与传统动力吸振器相比,含有阻尼较大吸振器的二重动力吸振器工作性能更好。
4 结论
在汽车振动领域,激振频率ω通常在较大范围内变化。虽然安装传统动力吸振器后,激振频率与吸振器固有频率相等时可以有效抑制零部件的共振,但吸振器的安装会使零部件产生新的共振峰。当激振频率变化时有可能使零部件再次处于共振点。本文对提出的二重动力吸振器进行建模、求解,并分析吸振器阻尼对主系统频率响应的影响,据此设计二重动力吸振器参数。在MATLAB/Simulink软件中搭建二重动力吸振器模型与传统动力吸振器模型,对吸振器的性能进行仿真。仿真结果表明:
(1)当二重动力吸振器中固有频率较大的吸振器与传统动力吸振器结构参数相同,在激振频率变化时,二重动力吸振器对应的主系统共振峰更低;
(2)激振频率处于吸振器减振点时,二重动力吸振器表现出与传统动力吸振器相同的减振效果。
本文仅根据理论分析设定二重动力吸振器的结构参数,未通过优化结构参数提升二重动力吸振器的工作性能;仿真的方式验证二重动力吸振器较传统动力吸振器性能的改善,并未将二重动力吸振器应用到汽车具体零部件振动的控制中,需要在今后的工作中不断完善。

